第二章 整式的加减 章末复习课件(60张PPT)
文档属性
| 名称 | 第二章 整式的加减 章末复习课件(60张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-14 00:00:00 | ||
图片预览










文档简介
(共60张PPT)
新课标 人教版 七年级上册
2023-2024学年度上学期人教版精品课件
第二章 整式的加减小结
1. 能用含有字母的式子表示实际问题中的数量关系;
2. 理解单项式、多项式、整式的定义;
3. 能准确找出单项式的系数、次数、多项式的项和次数;
4. 熟练进行整式的加减运算;
5. 会求代数式的值.
学习目标
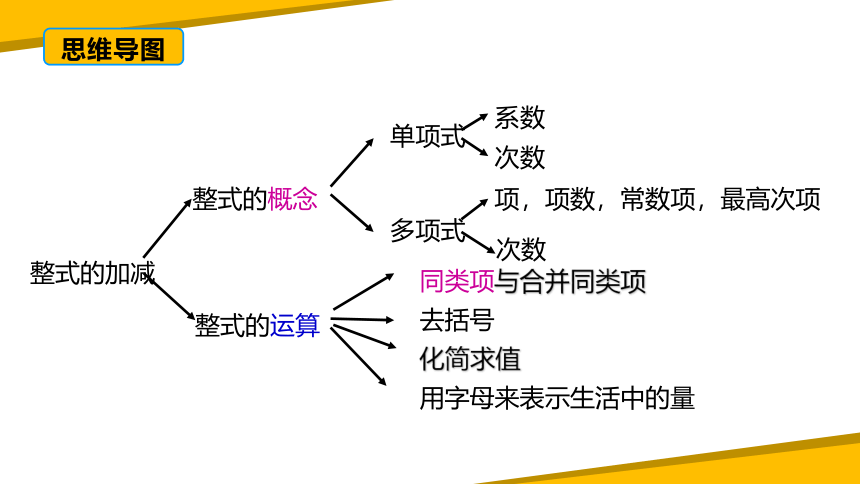
整式的加减
整式的概念
整式的运算
单项式
多项式
系数
次数
项,项数,常数项,最高次项
次数
同类项与合并同类项
去括号
化简求值
用字母来表示生活中的量
思维导图
1. 字母与字母相乘时省略乘号,例如:a×b可以写成ab;
2. 数字与字母相乘时,数字在前,字母在后,例如:100×t可以写成100t 、 0.8×m可以写成0.8m;
3. 1或-1与字母相乘时,1通常省略不写,例如1×a可以写成a,
-1×a可以写成-a;
4. 带分数与字母相乘时,把带分数化成假分数,例如 ×y必须写成 y ;
用字母表示数的特殊规定:
知识梳理
5. 相同字母相乘时应写成幂的形式,例如a×a可以写成a ;
6. 出现多个字母时,字母一般按照26个英文字母顺序排列;
7. 数与字母相除时,写成分数形式,例如n÷2可以写成 ;
8. 含有字母的式子表示数量关系时,若结果是加、减关系,有单位的必须把式子用括号括起来,再写单位,例如(2x+1.5y)元.
知识梳理
列式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言,在形式上更简单,使用上更方便(也把它称为代数式).
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式.
知识梳理
例1: (2022 吉林)篮球队要购买10个篮球,每个篮球m元,一共需要 元.(用含m的代数式表示)
【分析】根据题意直接列出代数式即可.
【解答】解:篮球队要买10个篮球,每个篮球m元,一共需要10m元,
故答案为:10m.
【点评】本题主要考查了通过实际问题列出代数式,理解题意是解答本题的关键.
例题讲解
例2: (2022 长沙)为落实“双减”政策,某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲,乙两种读本共100本供学生阅读,其中甲种读本的单价为10元/本,乙种读本的单价为8元/本,设购买甲种读本x本,则购买乙种读本的费用为( )
A.8x元B.10(100-x)元 C.8(100-x)元 D.(100-8x)元
【分析】直接利用乙的单价×乙的本数=乙的费用,进而得出答案.
【解答】解:设购买甲种读本x本,则购买乙种读本的费用为:8(100-x)元.故选:C.
【点评】此题主要考查了列代数式,正确表示出乙的本数是解题关键.
例题讲解
(2022 杭州)某体育比赛的门票分A票和B票两种,A票每张x元,B票每张y元.已知10张A票的总价与19张B票的总价相差320元,则( )
【分析】直接利用10张A票的总价与19张B票的总价相差320元,
得出等式求出答案.
【解答】解:由题意可得:|10x-19y|=320.
故选:C.
【点评】此题主要考查了列代数式,正确表示出两种门票的费用是解题关键.
A. B. C.|10x-19y|=320 D.|19x-10y|=320
巩固练习
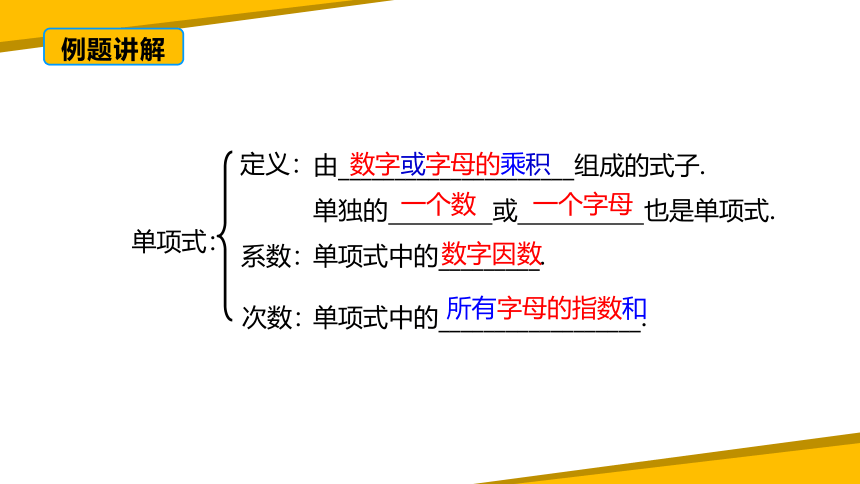
单项式:
定义:
系数:
次数:
由_____________________组成的式子.
单独的 或 也是单项式.
数字或字母的乘积
一个数
一个字母
单项式中的_________.
单项式中的__________________.
数字因数
所有字母的指数和
例题讲解
需要注意的问题:
1. 当单项式的系数是 1 或 -1 时,“1”通常省略不写.
2. 当式子分母中出现字母时不是单项式.
3. 圆周率 π 是常数,不要看成字母.
4. 当单项式的系数是带分数时,通常写成假分数.
5. 单项式的系数应包括它前面的性质符号.
6. 单项式次数是指所有字母的次数的和,与数字的次数没有关系.
7. 单独的数字不含字母,规定它的次数是零次.
知识梳理
例3:在式子3m+n,-2mn,p, ,0中,单项式的个数是( )
A. 3 B. 4 C. 5 D. 6
A
√
√
√
【解析】 -2mn,p,0是单项式. 故选A.
例题讲解
例4: (2022 广东)单项式3xy的系数为 .
【分析】应用单项式的定义进行判定即可得出答案.
【解答】解:单项式3xy的系数为3.
故答案为:3.
例题讲解
例5:下列各个式子中,书写格式正确的是( )
F
1. 代数式中用到乘法时,若是数字与数字乘,要用“× ”;若是数字与字母乘,乘号通常写成“.”或省略不写,如 3×a应写成3·a或3a,且数字与字母相乘时,字母与字母相乘,乘号通常写成“·” 或省略不写.
2. 带分数与字母相乘,要写成假分数.
3. 代数式中出现除法运算时,一般用分数写,即用分数线代替除号.
4. 系数一般写在字母的前面,且系数“1” 往往会省略.
例题讲解
3
代数式 的系数是 ,次数是 .
【易错提示】单项式的次数和系数、多项式的次数和项是容易混淆的概念,需辨别清楚.
巩固练习
多项式:
定义:几个__________.
项: 组成多项式中的_____________.
有几项,就叫做_________.
常数项:多项式中_______________.
多项式的次数:____________________________.
单项式的和
每一个单项式
几项式
不含字母的项
多项式中次数最高的项的次数
整式:___________________统称整式.
单项式与多项式
例题讲解
需要注意的问题:
1. 在确定多项式的项时,要连同它前面的符号.
2. 一个多项式的次数最高项的次数是几,就说这个多项式是几次多项式.
3. 在多项式中,每个单项式都是这个多项式的项,每一项都有系数,但对整个多项式来说,没有系数的概念,只有次数的概念.
例题讲解
例6 :下列多项式次数为 3 的是( )
C
注意:(1)多项式的次数不是所有项的次数的和,而是它的最高次项次数;
(2)多项式的每一项都包含它前面的符号;
(3)再强调一次,“π”当作数字,而不是字母.
A. -5x2+6x-1 B. πx2+x-1
C. a2b+ab+b2 D. x2y2-2x3-1
例题讲解
例7:请说出下列各多项式是几次几项式,并写出多项式的最高次项和常数项.
四
三
例题讲解
同类项:
同类项的定义:
合并同类项概念:
合并同类项法则:
1. 相同,
2. 相同.
字母
相同的字母的指数也
(两相同)
1.与________无关
2.与_____________无关.
系数
字母的位置
(两无关)
注意:几个常数项也是______
同类项.
.
把多项式中的同类项合并成一项
1.______相加减;
2._____________________不变.
系数
字母和字母的指数
知识梳理
例8:(2022 湘潭)下列整式与ab2为同类项的是( )
A.a2b B.-2ab2 C.ab D.ab2c
【分析】根据同类项的定义,所含字母相同,相同字母的指数也相同,即可判断.
【解答】解:在a2b,-2ab2,ab,ab2c四个整式中,与ab2为同类项的是:-2ab2,
故选:B.
例题讲解
例9:(2022 永州)若单项式3xmy与-2x6y是同类项,则m= .
【解答】解:因为3xmy与-2x6y是同类项,
所以m=6.
故答案为:6.
【点评】本题考查了同类项,掌握同类项的定义:所含字母相同,并且相同字母的指数也相同是解题的关键.
例题讲解
例10:若3xm+5y2与x3yn的和是单项式,求mn的值.
【解析】由题意可知 3xm+5y2与x3yn是同类项,所以x的指数和y的指数分别相等.
解:由题意得:m+5=3,n=2,所以m= -2.
所以mn=(-2)2=4.
例题讲解
例11: (2022 西藏)下列计算正确的是( )
A.2ab-ab=ab B.2ab+ab=2a2b2
C.4a3b2-2a =2a2b D.-2ab2-a2b =-3a2b2
【解答】解:A、2ab-ab=(2-1) ab=ab,计算正确,符合题意;
B、2ab+ab=(2+1) ab=3ab,计算不正确,不符合题意;
C、4a3b2与-2a不是同类项,不能合并,计算不正确,不符合题意;
D、-2ab2与-a2b不是同类项,不能合并,计算不正确,不符合题意.
故选:A.
例题讲解
例12: (2022 上海)计算:3a-2a= .
【解答】解:3a-2a=(3-2) a=a.
【点评】本题考查合并同类项、代数式的化简.同类项相加减,只把系数相加减,字母及字母的指数不变.
例题讲解
1. 若5x2 y与x m yn是同类项,则m= ,n= .
若单项式a2b与3am+n bn能合并,则m= ,n= .
2
1
1
1
只有同类项才能合并成一项
巩固练习
2.(2022 荆州)化简a-2a的结果是( )
A.-a B.a C.3a D.0
【分析】利用合并同类项的法则进行求解即可.
【解答】解:a-2a=(1-2) a =-a.
故选:A.
巩固练习
3.(2022 达州)计算:2a+3a= .
【分析】根据合并同类项的法则:把同类项的系数相加,所得结果作为系数,字母和字母的指数不变求解.
【解答】解:2a+3a=5a,
故答案为:5a.
巩固练习
整式的加减混合运算步骤(有括号先去括号)
(一)去括号
(按照先小括号,再中括号,最后大括号的顺序)
1. 如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同.
2. 如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
“去括号,看符号. 是 ‘+’号,不变号,是‘-’号,全变号”.
(二)计算
1. 找同类项,做好标记.
2. 利用加法的交换律和结合律把同类项放在一起.
3. 利用乘法分配律计算结果.
4. 按要求按“升”或“降”幂排列.
找
搬
并
排
知识梳理
例13:已知A=x3+2y3-xy2,B=-y3+x3+2xy2,
求:(1)A+B;(2)2B-2A.
【解析】 把A,B所指的式子分别代入计算.
解:(1)A+B=(x3+2y3-xy2)+(-y3+x3+2xy2)
=x3+2y3-xy2-y3+x3+2xy2
=2x3+y3+xy2.
(2)2B-2A=2(-y3+x3+2xy2)-2(x3+2y3-xy2)
=-2y3+2x3+4xy2-2x3-4y3+2xy2
=6xy2-6y3.
例题讲解
【方法技巧】 去括号时应注意:
(1)括号前是“-”号,去括号时括号内各项要改变符号;
(2)运用乘法分配律时不要漏乘其中的项.
例题讲解
例14:若A是一个三次多项式,B是一个四次多项式,则A+B一定是( )
A.三次多项式 B.四次多项式或单项式
C.七次多项式 D.四次七项式
【解析】A+B的最高次项一定是四次项,至于是否含有其它低次项不得而知,所以A+B只可能是四次多项式或单项式. 故选B.
B
你能举出对应的例子吗?
例题讲解
1.下列各项中,去括号正确的是( )
A.x2-(2x-y+2)=x2-2x+y+2
B.-(m+n)-mn=-m+n-mn
C.x-(5x-3y)+(2x-y)=-2x+2y
D.ab-(-ab+3)=3
C
巩固练习
2.若A是一个四次多项式,B是一个二次多项式,则A-B ( )
A.可能是六次多项式
B.可能是二次多项式
C.一定是四次多项式或单项式
D.可能是0
C
巩固练习
3.(2022 包头)若一个多项式加上3xy+2y2-8,结果得2xy+3y2-5,则这个多项式为 .
【解答】解:由题意得,这个多项式为:
(2xy+3y2-5)-(3xy+2y2-8)
=2xy+3y2-5-3xy-2y2+8
=y2-xy+3.
故答案为:y2-xy+3.
巩固练习
4.(2022 吉林)下面是一道例题及其解答过程的一部分,其中A是关于m的多项式.请写出多项式A,并将该例题的解答过程补充完整.
巩固练习
【解答】解:由题知,m(A)-6(m+1)
= m2+6m-6m-6
= m2-6,
因为m2+6m= m (m+6),
所以A为:m+6,
故答案为:m2-6.
巩固练习
【解析】 如果把x的值直接代入,分别求出A,B,C的值,然后再求3A+2B-36C的值显然很麻烦,不如先把原式化简,再把x值代入计算.
例15:已知A=3x2-x+2,B=x+1,C = ,求3A+2B-36C的值,其中x=-6.
例题讲解
【方法技巧】 在求多项式的值时,一般情况是多项式能化简的就先化简,然后再把字母的值代入化简后的式子中求值,化简的过程就是整式运算的过程.
解:
当x=-6时,原式=-(-6)+24=6+24=30.
例题讲解
1.(2022 湖北)先化简,再求值:4xy-2xy-(-3xy),其中x=2,y=-1.
【解答】解:4xy-2xy-(-3xy)
=4xy-2xy+3xy
=5xy,
当x=2,y=-1时,原式=5×2×(-1)=-10.
【点评】本题考查了整式的加减—化简求值,准确熟练地进行计算是解题的关键.
巩固练习
2. 化简后再求值:5x2-2y-8(x2-2y)+3(2x2-3y),其中|x+12|+(y-13)2=0.
分析:原式去括号合并得到最简结果,利用非负数的性质求出x与y的值,代入计算即可求出值.
解:原式=5x2-2y-8x2+16y+6x2-9y=3x2-5y.
因为|x+2|+(y-3)2=0,所以x+2=0,y-3=0,
即x=-2,y=3,则原式=12-15=-3.
巩固练习
设n表示自然数,用关于n的整式表示出来.
例16:从2开始连续的偶数相加,它们和的情况如下表:
加数的个数n 和s
1 2=1×2
2 2+4=6=2×3
3 2+4+6=12=3×4
4 2+4+6+8=20=4×5
…… ……
例题讲解
(1)s与n之间有什么关系?能否用一个关系式来表示?
分析:观察上表,
当n=1时,s=1×2,即第一个数字是1,第二个数字是2;
当n=2时,s=2+4=6=2×3,第一个数字是2,第二个数字是3,
依此类推,发现第一个数字是n,第二个数字比n大1.
解:⑴ s与n的关系为s=n(n+1).
例题讲解
小结:观察是解题的前提条件,当已知数据有很多组时,需要仔细观察,反复比较,才能发现其中的规律.
(2)计算2+4+6+8+……+2022.
解:当n= =1011时,
s=1011×(1011+1)=1023132.
即2+4+6+8+……+2022= 1023132.
例题讲解
观察下列图形:它们是按一定规律排列的,依照此规律,第2022个图形中共有________个五角星.
6067
【解析】可以发现每个图形的五角星个数都比前面一个图形的五角星个数多3个.由于第1个图形的五角星个数是3×1+1,所以第n个图形的五角星个数是3n+1,故第2022个图形五角星个数是3×2022+1=6067.
巩固练习
中考链接
A
A
中考链接
C
(7.5﹣10x)
中考链接
中考链接
1. [2020湖南湘潭中考]已知2xn+1y3与x4y3是同类项,则n的值是 ( )
A.2 B.3 C.4 D.5
【答案】B
【解析】根据题意得,n+1=4,所以n=3.故选B.
随堂测试
2. [2020江苏无锡中考]若x+y=2,z-y=-3,则x+z的值等于 ( )
A.5 B.1 C.-1 D.-5
【答案】C
【解析】因为x+y=2,z-y=-3,所以x+z=(x+y)+(z-y)=-1.故选C.
随堂测试
3. [2018河北中考]用一根长为a(单位:cm)的铁丝,首尾相接围成一个正方形.要将它按如图所示的方式向外等距扩1(单位:cm),得到新的正方形,则这根铁丝需增加 ( )
A.4 cm B.8 cm C.(a+4)cm D.(a+8)cm
【答案】B
【解析】根据题意,知原正方形的周长为a cm,则边长为 cm,所以新正方形的边长为(+2)cm,所以新正方形的周长为4(+2)=(a+8)(cm),所以这根铁丝需增加8 cm.故选B.
随堂测试
4. [2019湖北黄石中考]化简(9x-3)-2(x+1)的结果是 ( )
A.2x-2 B.x+1
C.5x+3 D.x-3
【答案】D
【解析】(9x-3)-2(x+1)=3x-1-2x-2=x-3.故选D.
随堂测试
5. [2020天津中考]计算x+7x-5x的结果等于 .
【答案】3x
随堂测试
6. [2020广东中考]已知x=5-y,xy=2,计算3x+3y-4xy的值为 .
【答案】7
【解析】根据题意得,x+y=5,xy=2,所以3x+3y-4xy=3(x+y)-4xy=3×5-4×2=15-8=7.
随堂测试
7. [2020江苏连云港中考]按照如图所示的计算程序,若x=2,则输出
的结果是 .
【答案】-26
【解析】把x=2代入,则10-x2=10-22=6>0;再把x=6代入,则10-x2=10-62=-26<0,故输出的
结果是-26.
随堂测试
8. [2020海南中考]海南黎锦有着悠久的历史,已被列入世界非物质文化遗产名录.如图是黎锦上的图案,每个图案都是由相同菱形构成的,若按照第1个图至第4个图中的规律编织图案,则第5个图中有 个菱形,第n个图中有
个菱形.(用含n的式子表示)
【答案】41 n2+(n-1)2
随堂测试
9. [2020湖南长沙中考]某数学老师在课外活动中做了一个有趣的游戏:首先发给A,B,C三个同学相同数量的扑克牌(假定发到每个同学手中的扑克牌数量足够多),然后依次完成以下三个步骤:
第一步,A同学拿出两张扑克牌给B同学;
第二步,C同学拿出三张扑克牌给B同学;
第三步,A同学手中此时有多少张扑克牌,B同学就拿出多少张扑克牌给A同学.
请你确定,最终B同学手中剩余的扑克牌的张数为 .
【答案】7
随堂测试
课堂小结
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
新课标 人教版 七年级上册
2023-2024学年度上学期人教版精品课件
第二章 整式的加减小结
1. 能用含有字母的式子表示实际问题中的数量关系;
2. 理解单项式、多项式、整式的定义;
3. 能准确找出单项式的系数、次数、多项式的项和次数;
4. 熟练进行整式的加减运算;
5. 会求代数式的值.
学习目标
整式的加减
整式的概念
整式的运算
单项式
多项式
系数
次数
项,项数,常数项,最高次项
次数
同类项与合并同类项
去括号
化简求值
用字母来表示生活中的量
思维导图
1. 字母与字母相乘时省略乘号,例如:a×b可以写成ab;
2. 数字与字母相乘时,数字在前,字母在后,例如:100×t可以写成100t 、 0.8×m可以写成0.8m;
3. 1或-1与字母相乘时,1通常省略不写,例如1×a可以写成a,
-1×a可以写成-a;
4. 带分数与字母相乘时,把带分数化成假分数,例如 ×y必须写成 y ;
用字母表示数的特殊规定:
知识梳理
5. 相同字母相乘时应写成幂的形式,例如a×a可以写成a ;
6. 出现多个字母时,字母一般按照26个英文字母顺序排列;
7. 数与字母相除时,写成分数形式,例如n÷2可以写成 ;
8. 含有字母的式子表示数量关系时,若结果是加、减关系,有单位的必须把式子用括号括起来,再写单位,例如(2x+1.5y)元.
知识梳理
列式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言,在形式上更简单,使用上更方便(也把它称为代数式).
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式.
知识梳理
例1: (2022 吉林)篮球队要购买10个篮球,每个篮球m元,一共需要 元.(用含m的代数式表示)
【分析】根据题意直接列出代数式即可.
【解答】解:篮球队要买10个篮球,每个篮球m元,一共需要10m元,
故答案为:10m.
【点评】本题主要考查了通过实际问题列出代数式,理解题意是解答本题的关键.
例题讲解
例2: (2022 长沙)为落实“双减”政策,某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲,乙两种读本共100本供学生阅读,其中甲种读本的单价为10元/本,乙种读本的单价为8元/本,设购买甲种读本x本,则购买乙种读本的费用为( )
A.8x元B.10(100-x)元 C.8(100-x)元 D.(100-8x)元
【分析】直接利用乙的单价×乙的本数=乙的费用,进而得出答案.
【解答】解:设购买甲种读本x本,则购买乙种读本的费用为:8(100-x)元.故选:C.
【点评】此题主要考查了列代数式,正确表示出乙的本数是解题关键.
例题讲解
(2022 杭州)某体育比赛的门票分A票和B票两种,A票每张x元,B票每张y元.已知10张A票的总价与19张B票的总价相差320元,则( )
【分析】直接利用10张A票的总价与19张B票的总价相差320元,
得出等式求出答案.
【解答】解:由题意可得:|10x-19y|=320.
故选:C.
【点评】此题主要考查了列代数式,正确表示出两种门票的费用是解题关键.
A. B. C.|10x-19y|=320 D.|19x-10y|=320
巩固练习
单项式:
定义:
系数:
次数:
由_____________________组成的式子.
单独的 或 也是单项式.
数字或字母的乘积
一个数
一个字母
单项式中的_________.
单项式中的__________________.
数字因数
所有字母的指数和
例题讲解
需要注意的问题:
1. 当单项式的系数是 1 或 -1 时,“1”通常省略不写.
2. 当式子分母中出现字母时不是单项式.
3. 圆周率 π 是常数,不要看成字母.
4. 当单项式的系数是带分数时,通常写成假分数.
5. 单项式的系数应包括它前面的性质符号.
6. 单项式次数是指所有字母的次数的和,与数字的次数没有关系.
7. 单独的数字不含字母,规定它的次数是零次.
知识梳理
例3:在式子3m+n,-2mn,p, ,0中,单项式的个数是( )
A. 3 B. 4 C. 5 D. 6
A
√
√
√
【解析】 -2mn,p,0是单项式. 故选A.
例题讲解
例4: (2022 广东)单项式3xy的系数为 .
【分析】应用单项式的定义进行判定即可得出答案.
【解答】解:单项式3xy的系数为3.
故答案为:3.
例题讲解
例5:下列各个式子中,书写格式正确的是( )
F
1. 代数式中用到乘法时,若是数字与数字乘,要用“× ”;若是数字与字母乘,乘号通常写成“.”或省略不写,如 3×a应写成3·a或3a,且数字与字母相乘时,字母与字母相乘,乘号通常写成“·” 或省略不写.
2. 带分数与字母相乘,要写成假分数.
3. 代数式中出现除法运算时,一般用分数写,即用分数线代替除号.
4. 系数一般写在字母的前面,且系数“1” 往往会省略.
例题讲解
3
代数式 的系数是 ,次数是 .
【易错提示】单项式的次数和系数、多项式的次数和项是容易混淆的概念,需辨别清楚.
巩固练习
多项式:
定义:几个__________.
项: 组成多项式中的_____________.
有几项,就叫做_________.
常数项:多项式中_______________.
多项式的次数:____________________________.
单项式的和
每一个单项式
几项式
不含字母的项
多项式中次数最高的项的次数
整式:___________________统称整式.
单项式与多项式
例题讲解
需要注意的问题:
1. 在确定多项式的项时,要连同它前面的符号.
2. 一个多项式的次数最高项的次数是几,就说这个多项式是几次多项式.
3. 在多项式中,每个单项式都是这个多项式的项,每一项都有系数,但对整个多项式来说,没有系数的概念,只有次数的概念.
例题讲解
例6 :下列多项式次数为 3 的是( )
C
注意:(1)多项式的次数不是所有项的次数的和,而是它的最高次项次数;
(2)多项式的每一项都包含它前面的符号;
(3)再强调一次,“π”当作数字,而不是字母.
A. -5x2+6x-1 B. πx2+x-1
C. a2b+ab+b2 D. x2y2-2x3-1
例题讲解
例7:请说出下列各多项式是几次几项式,并写出多项式的最高次项和常数项.
四
三
例题讲解
同类项:
同类项的定义:
合并同类项概念:
合并同类项法则:
1. 相同,
2. 相同.
字母
相同的字母的指数也
(两相同)
1.与________无关
2.与_____________无关.
系数
字母的位置
(两无关)
注意:几个常数项也是______
同类项.
.
把多项式中的同类项合并成一项
1.______相加减;
2._____________________不变.
系数
字母和字母的指数
知识梳理
例8:(2022 湘潭)下列整式与ab2为同类项的是( )
A.a2b B.-2ab2 C.ab D.ab2c
【分析】根据同类项的定义,所含字母相同,相同字母的指数也相同,即可判断.
【解答】解:在a2b,-2ab2,ab,ab2c四个整式中,与ab2为同类项的是:-2ab2,
故选:B.
例题讲解
例9:(2022 永州)若单项式3xmy与-2x6y是同类项,则m= .
【解答】解:因为3xmy与-2x6y是同类项,
所以m=6.
故答案为:6.
【点评】本题考查了同类项,掌握同类项的定义:所含字母相同,并且相同字母的指数也相同是解题的关键.
例题讲解
例10:若3xm+5y2与x3yn的和是单项式,求mn的值.
【解析】由题意可知 3xm+5y2与x3yn是同类项,所以x的指数和y的指数分别相等.
解:由题意得:m+5=3,n=2,所以m= -2.
所以mn=(-2)2=4.
例题讲解
例11: (2022 西藏)下列计算正确的是( )
A.2ab-ab=ab B.2ab+ab=2a2b2
C.4a3b2-2a =2a2b D.-2ab2-a2b =-3a2b2
【解答】解:A、2ab-ab=(2-1) ab=ab,计算正确,符合题意;
B、2ab+ab=(2+1) ab=3ab,计算不正确,不符合题意;
C、4a3b2与-2a不是同类项,不能合并,计算不正确,不符合题意;
D、-2ab2与-a2b不是同类项,不能合并,计算不正确,不符合题意.
故选:A.
例题讲解
例12: (2022 上海)计算:3a-2a= .
【解答】解:3a-2a=(3-2) a=a.
【点评】本题考查合并同类项、代数式的化简.同类项相加减,只把系数相加减,字母及字母的指数不变.
例题讲解
1. 若5x2 y与x m yn是同类项,则m= ,n= .
若单项式a2b与3am+n bn能合并,则m= ,n= .
2
1
1
1
只有同类项才能合并成一项
巩固练习
2.(2022 荆州)化简a-2a的结果是( )
A.-a B.a C.3a D.0
【分析】利用合并同类项的法则进行求解即可.
【解答】解:a-2a=(1-2) a =-a.
故选:A.
巩固练习
3.(2022 达州)计算:2a+3a= .
【分析】根据合并同类项的法则:把同类项的系数相加,所得结果作为系数,字母和字母的指数不变求解.
【解答】解:2a+3a=5a,
故答案为:5a.
巩固练习
整式的加减混合运算步骤(有括号先去括号)
(一)去括号
(按照先小括号,再中括号,最后大括号的顺序)
1. 如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同.
2. 如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
“去括号,看符号. 是 ‘+’号,不变号,是‘-’号,全变号”.
(二)计算
1. 找同类项,做好标记.
2. 利用加法的交换律和结合律把同类项放在一起.
3. 利用乘法分配律计算结果.
4. 按要求按“升”或“降”幂排列.
找
搬
并
排
知识梳理
例13:已知A=x3+2y3-xy2,B=-y3+x3+2xy2,
求:(1)A+B;(2)2B-2A.
【解析】 把A,B所指的式子分别代入计算.
解:(1)A+B=(x3+2y3-xy2)+(-y3+x3+2xy2)
=x3+2y3-xy2-y3+x3+2xy2
=2x3+y3+xy2.
(2)2B-2A=2(-y3+x3+2xy2)-2(x3+2y3-xy2)
=-2y3+2x3+4xy2-2x3-4y3+2xy2
=6xy2-6y3.
例题讲解
【方法技巧】 去括号时应注意:
(1)括号前是“-”号,去括号时括号内各项要改变符号;
(2)运用乘法分配律时不要漏乘其中的项.
例题讲解
例14:若A是一个三次多项式,B是一个四次多项式,则A+B一定是( )
A.三次多项式 B.四次多项式或单项式
C.七次多项式 D.四次七项式
【解析】A+B的最高次项一定是四次项,至于是否含有其它低次项不得而知,所以A+B只可能是四次多项式或单项式. 故选B.
B
你能举出对应的例子吗?
例题讲解
1.下列各项中,去括号正确的是( )
A.x2-(2x-y+2)=x2-2x+y+2
B.-(m+n)-mn=-m+n-mn
C.x-(5x-3y)+(2x-y)=-2x+2y
D.ab-(-ab+3)=3
C
巩固练习
2.若A是一个四次多项式,B是一个二次多项式,则A-B ( )
A.可能是六次多项式
B.可能是二次多项式
C.一定是四次多项式或单项式
D.可能是0
C
巩固练习
3.(2022 包头)若一个多项式加上3xy+2y2-8,结果得2xy+3y2-5,则这个多项式为 .
【解答】解:由题意得,这个多项式为:
(2xy+3y2-5)-(3xy+2y2-8)
=2xy+3y2-5-3xy-2y2+8
=y2-xy+3.
故答案为:y2-xy+3.
巩固练习
4.(2022 吉林)下面是一道例题及其解答过程的一部分,其中A是关于m的多项式.请写出多项式A,并将该例题的解答过程补充完整.
巩固练习
【解答】解:由题知,m(A)-6(m+1)
= m2+6m-6m-6
= m2-6,
因为m2+6m= m (m+6),
所以A为:m+6,
故答案为:m2-6.
巩固练习
【解析】 如果把x的值直接代入,分别求出A,B,C的值,然后再求3A+2B-36C的值显然很麻烦,不如先把原式化简,再把x值代入计算.
例15:已知A=3x2-x+2,B=x+1,C = ,求3A+2B-36C的值,其中x=-6.
例题讲解
【方法技巧】 在求多项式的值时,一般情况是多项式能化简的就先化简,然后再把字母的值代入化简后的式子中求值,化简的过程就是整式运算的过程.
解:
当x=-6时,原式=-(-6)+24=6+24=30.
例题讲解
1.(2022 湖北)先化简,再求值:4xy-2xy-(-3xy),其中x=2,y=-1.
【解答】解:4xy-2xy-(-3xy)
=4xy-2xy+3xy
=5xy,
当x=2,y=-1时,原式=5×2×(-1)=-10.
【点评】本题考查了整式的加减—化简求值,准确熟练地进行计算是解题的关键.
巩固练习
2. 化简后再求值:5x2-2y-8(x2-2y)+3(2x2-3y),其中|x+12|+(y-13)2=0.
分析:原式去括号合并得到最简结果,利用非负数的性质求出x与y的值,代入计算即可求出值.
解:原式=5x2-2y-8x2+16y+6x2-9y=3x2-5y.
因为|x+2|+(y-3)2=0,所以x+2=0,y-3=0,
即x=-2,y=3,则原式=12-15=-3.
巩固练习
设n表示自然数,用关于n的整式表示出来.
例16:从2开始连续的偶数相加,它们和的情况如下表:
加数的个数n 和s
1 2=1×2
2 2+4=6=2×3
3 2+4+6=12=3×4
4 2+4+6+8=20=4×5
…… ……
例题讲解
(1)s与n之间有什么关系?能否用一个关系式来表示?
分析:观察上表,
当n=1时,s=1×2,即第一个数字是1,第二个数字是2;
当n=2时,s=2+4=6=2×3,第一个数字是2,第二个数字是3,
依此类推,发现第一个数字是n,第二个数字比n大1.
解:⑴ s与n的关系为s=n(n+1).
例题讲解
小结:观察是解题的前提条件,当已知数据有很多组时,需要仔细观察,反复比较,才能发现其中的规律.
(2)计算2+4+6+8+……+2022.
解:当n= =1011时,
s=1011×(1011+1)=1023132.
即2+4+6+8+……+2022= 1023132.
例题讲解
观察下列图形:它们是按一定规律排列的,依照此规律,第2022个图形中共有________个五角星.
6067
【解析】可以发现每个图形的五角星个数都比前面一个图形的五角星个数多3个.由于第1个图形的五角星个数是3×1+1,所以第n个图形的五角星个数是3n+1,故第2022个图形五角星个数是3×2022+1=6067.
巩固练习
中考链接
A
A
中考链接
C
(7.5﹣10x)
中考链接
中考链接
1. [2020湖南湘潭中考]已知2xn+1y3与x4y3是同类项,则n的值是 ( )
A.2 B.3 C.4 D.5
【答案】B
【解析】根据题意得,n+1=4,所以n=3.故选B.
随堂测试
2. [2020江苏无锡中考]若x+y=2,z-y=-3,则x+z的值等于 ( )
A.5 B.1 C.-1 D.-5
【答案】C
【解析】因为x+y=2,z-y=-3,所以x+z=(x+y)+(z-y)=-1.故选C.
随堂测试
3. [2018河北中考]用一根长为a(单位:cm)的铁丝,首尾相接围成一个正方形.要将它按如图所示的方式向外等距扩1(单位:cm),得到新的正方形,则这根铁丝需增加 ( )
A.4 cm B.8 cm C.(a+4)cm D.(a+8)cm
【答案】B
【解析】根据题意,知原正方形的周长为a cm,则边长为 cm,所以新正方形的边长为(+2)cm,所以新正方形的周长为4(+2)=(a+8)(cm),所以这根铁丝需增加8 cm.故选B.
随堂测试
4. [2019湖北黄石中考]化简(9x-3)-2(x+1)的结果是 ( )
A.2x-2 B.x+1
C.5x+3 D.x-3
【答案】D
【解析】(9x-3)-2(x+1)=3x-1-2x-2=x-3.故选D.
随堂测试
5. [2020天津中考]计算x+7x-5x的结果等于 .
【答案】3x
随堂测试
6. [2020广东中考]已知x=5-y,xy=2,计算3x+3y-4xy的值为 .
【答案】7
【解析】根据题意得,x+y=5,xy=2,所以3x+3y-4xy=3(x+y)-4xy=3×5-4×2=15-8=7.
随堂测试
7. [2020江苏连云港中考]按照如图所示的计算程序,若x=2,则输出
的结果是 .
【答案】-26
【解析】把x=2代入,则10-x2=10-22=6>0;再把x=6代入,则10-x2=10-62=-26<0,故输出的
结果是-26.
随堂测试
8. [2020海南中考]海南黎锦有着悠久的历史,已被列入世界非物质文化遗产名录.如图是黎锦上的图案,每个图案都是由相同菱形构成的,若按照第1个图至第4个图中的规律编织图案,则第5个图中有 个菱形,第n个图中有
个菱形.(用含n的式子表示)
【答案】41 n2+(n-1)2
随堂测试
9. [2020湖南长沙中考]某数学老师在课外活动中做了一个有趣的游戏:首先发给A,B,C三个同学相同数量的扑克牌(假定发到每个同学手中的扑克牌数量足够多),然后依次完成以下三个步骤:
第一步,A同学拿出两张扑克牌给B同学;
第二步,C同学拿出三张扑克牌给B同学;
第三步,A同学手中此时有多少张扑克牌,B同学就拿出多少张扑克牌给A同学.
请你确定,最终B同学手中剩余的扑克牌的张数为 .
【答案】7
随堂测试
课堂小结
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
