22.1.4二次函数y=ax^2+bx+c的图象和性质(第二课时) 课件(35张PPT)
文档属性
| 名称 | 22.1.4二次函数y=ax^2+bx+c的图象和性质(第二课时) 课件(35张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-14 10:01:02 | ||
图片预览











文档简介
(共35张PPT)
新课标 人教版 九年级上册
2023-2024学年度上学期人教版精品课件
第二十二章二次函数
22.1.4二次函数y=ax +bx+c的图象和性质(第二课时)用待定系数法求二次函数的解析式
学习目标
1. 会用待定系数法确定二次函数y=ax2+bx+c的解析式.
2.通过确定二次函数解析式的过程,体会综合运用函数解析式和过函数图象上的点的数形结合思想.
3 .理解并掌握二次函数图象与各项系数之间的关系.
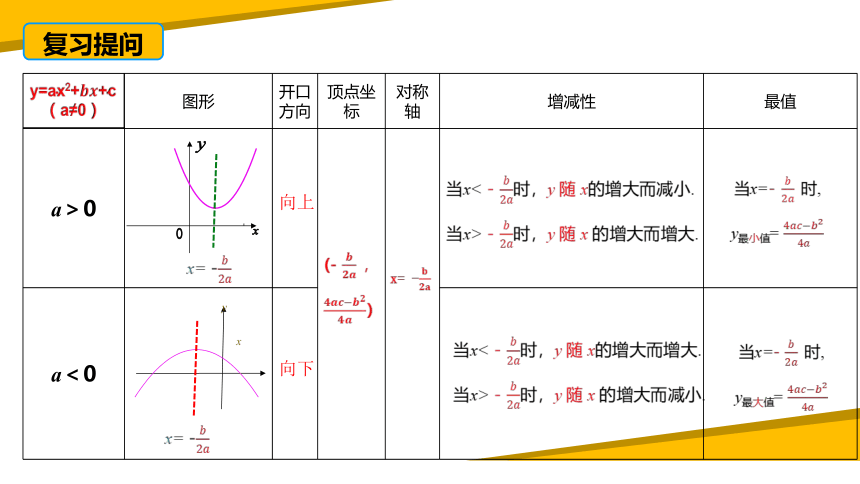
复习提问
向上
向下
y
x
【问题】若二次函数经过(-1,10)、(1,4)、(2,7)三个点,能求出二次函数的解析式吗?
探究新知
【问题】已知抛物线的顶点为(-1,-3),与y轴交点为(0,-5),求抛物线的解析式.
由题意可得,抛物线的顶点为(-1,-3)
设所求二次函数为y=a(x+1)2-3.
∵函数图象经过点(0,-5),
∴a(0+1)2-3=-5.
解得a=-2.
所求二次函数是y=-2(x+1)2-3.
探究新知
【问题】已知二次函数的图像经过点(-3,0),(-1,0),(0,-3),试求这个二次函数的解析式.
解:∵(-3,0),(-1,0)是抛物线y=ax2+bx+c与x轴的交点.
∴当y=0时,x1=-3, x2=-1.
而方程a(x+3)(x+1)=0的两根为:x1=-3, x2=-1.
∴设这个二次函数的解析式是y=a(x+3)(x+1).
∵函数图象经过点(0,-3),
∴ a(0+3)(0+1) =-3.
解得a=-1.
所求二次函数是y=- (x+3)(x+1),即y=-x2-4x-3
探究新知
3)交点式y=a(x-x1)(x-x2).当抛物线与x轴的两个交点为(x1,0)、(x2,0)时,可设y=a(x-x1)(x-x2),再将另一点的坐标代入即可求出a的值,从而写出二次函数的解析式.
求二次函数解析式的一般方法:
1)一般式y=ax2+bx+c.代入三个点的坐标列出关于a, b, c的方程组,并求出a, b, c,就可以写出二次函数的解析式.
2)顶点式y=a(x-h)2+k.根据顶坐标点(h,k),可设顶点式y=a(x-h)2+k,再将另一点的坐标代入,即可求出a的值,从而写出二次函数的解析式.
探究新知
典例解析
例1.已知二次函数的图象过(-1,-9)、(1,-3)
和(3,-5)三点,求此二次函数的解析式 .
解:设此二次函数的解析式为
由题意得:
∴二次函数的解析式为y= -x2+3x-5.
典例解析
例2.已知二次函数的图象以A(-1,4)为顶点,且过点B(2,-5),求该函数的解析式 .
解:设此二次函数的解析式为
∵函数过点B(2,-5)
∴a× (2+1)2+4= -5
解得a= -1
∴二次函数的解析式为
∴即
典例解析
<
例3. 已知抛物线与x轴交于点(1,0),(3,0),且图象过点(0,-3) ,求这个二次函数解析式.
解:设此二次函数的解析式为
由题意得:
∴二次函数的解析式为y= -x2+4x-3.
典例解析
例4.已知二次函数的图象如图所示,求此抛物线的解析式.
y
x
o
x=1
3
3
∴二次函数的解析式为y= -x2+2x+3.
解:由图可知函数图象经过点(3,0),(0,3).
随堂练习
随堂练习
随堂练习
随堂练习
4.
随堂练习
5.
中考链接
1.(2023·上海)一个二次函数y=ax2+bx+c的顶点在y轴正半轴上,且其对称轴左侧的部分是上升的,那么这个二次函数的解析式可以是______________.
2.(2023·绍兴)已知二次函数y=-x2+bx+c.
(1)当b=4,c=3时,
①求该函数图象的顶点坐标;
②当-1 ≤ x ≤ 3时,求y的取值范围
(2)当x ≤ 0时,y的最大值为2;当x>0时,y的最大值为3,求二次函数的表达式
y=-x2+1(答案不唯一)
中考链接
【解答】解:(1)①∵b=4,c=3时,
∴y=-x2+4x+3=-(x-2)2+7,
∴顶点坐标为(2,7)
②∵-1 ≤ x ≤ 3中含有顶点(2,7),
∴当x=2时,y有最大值7,
∵ 2-(-1)>3-2,
∴当x=-1时,y有最小值为:-2,
∴当-1 ≤ x ≤ 3时,-2 ≤ y ≤ 7
(2)∵x ≤ 0时,y的最大值为2;x>0时,y的最大值为3,
∴抛物线的对称轴 2一员在y轴的右侧,
∴b>0.
∵抛物线开□向下,x<0时,y的最大值为2,
∴c=2.
又∵
∴b=±2,
∵ b>0.
∴ b=2.
∴二次函数的表达式为y=-x2+2x+2.
中考链接
3. (2023·宁波)如图,已知二次函数y=x2+bx+c图象经过点A(1,-2)和B(0,-5)
(1)求该二次函数的表达式及图象的顶点坐标
(2)当y ≤ -2时,请根据图象直接写出x的取值范围
解:(1)把A(1.-2)和B(0.-5)代入y=x2+bx+c得:1+b+c=-2,c=-5
解得b=2,c=-5
∴二次函数的表达式为y=x2+2x-5.
∵y=x2+2x-5=(x+1)2-6,
∴顶点坐标为(-1,-6)
中考链接
(2)如图:
∵点A(1.-2)关于对称轴直线x=-1的对称点C(-3,-2).
∴当y ≤ -2时,x的范围是-3 ≤ x ≤ 1.
课堂小结
1.本节课学了哪些主要内容?
2.确定解析式的关键是什么?
3.简述二次函数y=ax2+bx+c(a≠0)图象与各项系数之间的关系?
当堂测试
D
B
当堂测试
D
y=8x2+20x+12
y=2(x-1)2-3或y=-2(x-1)2-3
当堂测试
当堂测试
当堂测试
当堂测试
分层作业
B
C
分层作业
分层作业
y=x2-5x+4
y=2x2-8x+5
分层作业
分层作业
分层作业
分层作业
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
新课标 人教版 九年级上册
2023-2024学年度上学期人教版精品课件
第二十二章二次函数
22.1.4二次函数y=ax +bx+c的图象和性质(第二课时)用待定系数法求二次函数的解析式
学习目标
1. 会用待定系数法确定二次函数y=ax2+bx+c的解析式.
2.通过确定二次函数解析式的过程,体会综合运用函数解析式和过函数图象上的点的数形结合思想.
3 .理解并掌握二次函数图象与各项系数之间的关系.
复习提问
向上
向下
y
x
【问题】若二次函数经过(-1,10)、(1,4)、(2,7)三个点,能求出二次函数的解析式吗?
探究新知
【问题】已知抛物线的顶点为(-1,-3),与y轴交点为(0,-5),求抛物线的解析式.
由题意可得,抛物线的顶点为(-1,-3)
设所求二次函数为y=a(x+1)2-3.
∵函数图象经过点(0,-5),
∴a(0+1)2-3=-5.
解得a=-2.
所求二次函数是y=-2(x+1)2-3.
探究新知
【问题】已知二次函数的图像经过点(-3,0),(-1,0),(0,-3),试求这个二次函数的解析式.
解:∵(-3,0),(-1,0)是抛物线y=ax2+bx+c与x轴的交点.
∴当y=0时,x1=-3, x2=-1.
而方程a(x+3)(x+1)=0的两根为:x1=-3, x2=-1.
∴设这个二次函数的解析式是y=a(x+3)(x+1).
∵函数图象经过点(0,-3),
∴ a(0+3)(0+1) =-3.
解得a=-1.
所求二次函数是y=- (x+3)(x+1),即y=-x2-4x-3
探究新知
3)交点式y=a(x-x1)(x-x2).当抛物线与x轴的两个交点为(x1,0)、(x2,0)时,可设y=a(x-x1)(x-x2),再将另一点的坐标代入即可求出a的值,从而写出二次函数的解析式.
求二次函数解析式的一般方法:
1)一般式y=ax2+bx+c.代入三个点的坐标列出关于a, b, c的方程组,并求出a, b, c,就可以写出二次函数的解析式.
2)顶点式y=a(x-h)2+k.根据顶坐标点(h,k),可设顶点式y=a(x-h)2+k,再将另一点的坐标代入,即可求出a的值,从而写出二次函数的解析式.
探究新知
典例解析
例1.已知二次函数的图象过(-1,-9)、(1,-3)
和(3,-5)三点,求此二次函数的解析式 .
解:设此二次函数的解析式为
由题意得:
∴二次函数的解析式为y= -x2+3x-5.
典例解析
例2.已知二次函数的图象以A(-1,4)为顶点,且过点B(2,-5),求该函数的解析式 .
解:设此二次函数的解析式为
∵函数过点B(2,-5)
∴a× (2+1)2+4= -5
解得a= -1
∴二次函数的解析式为
∴即
典例解析
<
例3. 已知抛物线与x轴交于点(1,0),(3,0),且图象过点(0,-3) ,求这个二次函数解析式.
解:设此二次函数的解析式为
由题意得:
∴二次函数的解析式为y= -x2+4x-3.
典例解析
例4.已知二次函数的图象如图所示,求此抛物线的解析式.
y
x
o
x=1
3
3
∴二次函数的解析式为y= -x2+2x+3.
解:由图可知函数图象经过点(3,0),(0,3).
随堂练习
随堂练习
随堂练习
随堂练习
4.
随堂练习
5.
中考链接
1.(2023·上海)一个二次函数y=ax2+bx+c的顶点在y轴正半轴上,且其对称轴左侧的部分是上升的,那么这个二次函数的解析式可以是______________.
2.(2023·绍兴)已知二次函数y=-x2+bx+c.
(1)当b=4,c=3时,
①求该函数图象的顶点坐标;
②当-1 ≤ x ≤ 3时,求y的取值范围
(2)当x ≤ 0时,y的最大值为2;当x>0时,y的最大值为3,求二次函数的表达式
y=-x2+1(答案不唯一)
中考链接
【解答】解:(1)①∵b=4,c=3时,
∴y=-x2+4x+3=-(x-2)2+7,
∴顶点坐标为(2,7)
②∵-1 ≤ x ≤ 3中含有顶点(2,7),
∴当x=2时,y有最大值7,
∵ 2-(-1)>3-2,
∴当x=-1时,y有最小值为:-2,
∴当-1 ≤ x ≤ 3时,-2 ≤ y ≤ 7
(2)∵x ≤ 0时,y的最大值为2;x>0时,y的最大值为3,
∴抛物线的对称轴 2一员在y轴的右侧,
∴b>0.
∵抛物线开□向下,x<0时,y的最大值为2,
∴c=2.
又∵
∴b=±2,
∵ b>0.
∴ b=2.
∴二次函数的表达式为y=-x2+2x+2.
中考链接
3. (2023·宁波)如图,已知二次函数y=x2+bx+c图象经过点A(1,-2)和B(0,-5)
(1)求该二次函数的表达式及图象的顶点坐标
(2)当y ≤ -2时,请根据图象直接写出x的取值范围
解:(1)把A(1.-2)和B(0.-5)代入y=x2+bx+c得:1+b+c=-2,c=-5
解得b=2,c=-5
∴二次函数的表达式为y=x2+2x-5.
∵y=x2+2x-5=(x+1)2-6,
∴顶点坐标为(-1,-6)
中考链接
(2)如图:
∵点A(1.-2)关于对称轴直线x=-1的对称点C(-3,-2).
∴当y ≤ -2时,x的范围是-3 ≤ x ≤ 1.
课堂小结
1.本节课学了哪些主要内容?
2.确定解析式的关键是什么?
3.简述二次函数y=ax2+bx+c(a≠0)图象与各项系数之间的关系?
当堂测试
D
B
当堂测试
D
y=8x2+20x+12
y=2(x-1)2-3或y=-2(x-1)2-3
当堂测试
当堂测试
当堂测试
当堂测试
分层作业
B
C
分层作业
分层作业
y=x2-5x+4
y=2x2-8x+5
分层作业
分层作业
分层作业
分层作业
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
同课章节目录
