第14章 勾股定理》直角三角形三边的关系(江苏省无锡市)
文档属性
| 名称 | 第14章 勾股定理》直角三角形三边的关系(江苏省无锡市) |

|
|
| 格式 | rar | ||
| 文件大小 | 15.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-13 23:35:00 | ||
图片预览






文档简介
课件21张PPT。14.1.1 直角三角形三边的关系(2) 勾股定理(gou-gu theorem) 如果直角三角形两直角边分别为a、b,斜边为c,那么 即直角三角形两直角边的平方和等于斜边的平方。你知道“勾”和“股”的由来吗? 我国发现勾股定理的时间比较早,在公元前一世纪《周髀算经》里记载着夏禹(公元前21世纪)和商高(公元前1120年)发现了这个定理。由于古书中记有“勾广三,股修四,径隅五”,因此这个定理就称为“ 勾股定理”。 西方的勾股定理之父——毕达哥拉斯
?
????????????????????????????????????????????????????????????????????????????????????
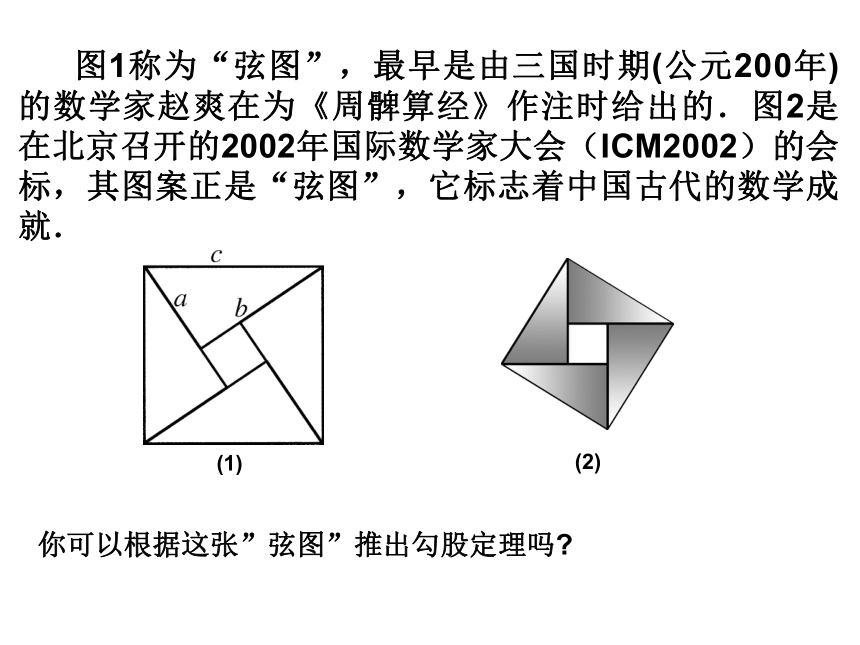
(Pythagoras, 约公元前580~前500) 在西方最早发现这个定理的相传是公元前五百多年古希腊数学家毕达哥拉斯,所以西方称它“毕达哥拉斯定理”.abcaaabbbcccS正方形ABCD=(a+b)(a+b)=(a+b)2ACDBS正方形ABCD=+S小绿正方形4×S红直角三角形 图形经过割补拼接后,只要没有空隙,没有重叠,面积不会改变。∴ a2+b2=c2 图1称为“弦图”,最早是由三国时期(公元200年)的数学家赵爽在为《周髀算经》作注时给出的.图2是在北京召开的2002年国际数学家大会(ICM2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.
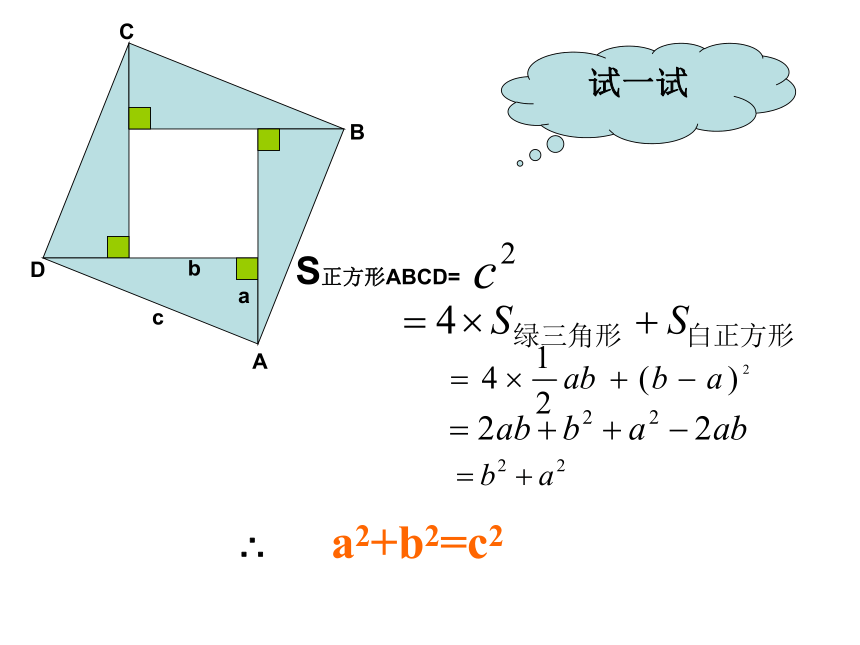
你可以根据这张”弦图”推出勾股定理吗?(1)(2)S正方形ABCD=
∴ a2+b2=c2试一试如图有两个一模一样的直角三角形,两直角边为a,b斜边为c,另一个大的是一个等腰直角三角形,直角边为c,请开动脑筋,把他拼成一个可以证明勾股定理的图形,
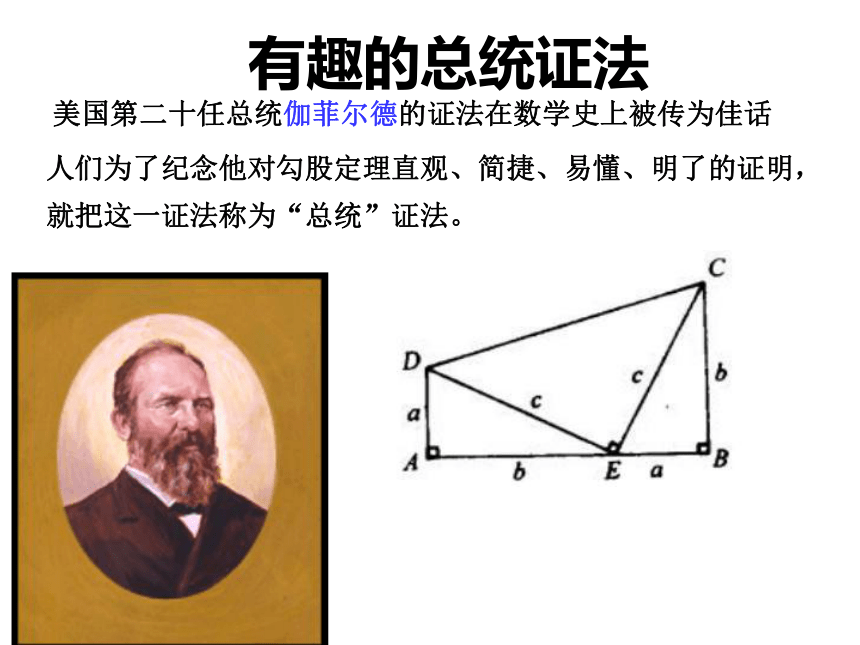
拼一拼美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法。 有趣的总统证法aabbccABCDE1.如图,受台风韦伯影响,一棵树在离地面4米处断裂, 树的顶部落在离树跟底部3米处,这棵树折断前有多高?应用知识回归生活应用知识回归生活王子救公主的故事营救方案小船能漂多远?4. 如图,为了求出湖两岸的AB两点之间的距离,一个观测者在点C设桩,使△ABC恰好为Rt△,通过测量,得到AC长160米,BC长128米,问从A点穿过湖到点B有多远?
解:Rt△ABC中,AC=160,BC=128,
根据勾股定理得:
答:从A点穿过湖到点B有96米。应用知识回归生活x5. 假期中,王强和同学到某海岛上去探宝旅游,按照探宝图(如图),他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A到宝藏埋藏点B的直线距离是多少千米?应用知识回归生活 做一个长,宽,高分别为50厘米,40厘米,30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明。练一练:30cm40cm50cm1图形经过割补拼接后,只要没有空隙,没有重叠,面积不会改变。小 结:2构造直角三角形,将实际问题转化为数学问题,
运用勾股定理建立方程求解。 作业:1.网上搜索有关勾股定理的其他证明(拼图),并结合自己的观 点完成一篇400字左右的论文.
2.完成书后的习题p53,练习1,2 毕达哥拉斯创建了政治、宗教、数学合一的秘密学术团体,这个团体被后人称为毕达哥拉斯学派。
这个学派的活动都是秘密的,笼罩着一种不可思议的神秘气氛。据说,每个新入学的学生都得宣誓严守秘密,并终身只加入这一学派。该学派还有一种习惯,就是将一切发明都归之于学派的领袖,而且秘而不宣,以致后人不知是何人在何时所发明的。
毕达哥拉斯定理(即勾股定理)是毕达哥拉斯的一大贡献,他的一个学生希帕索斯通过勾股定理发现了无理数,虽然这一发现打破了毕达哥拉斯宇宙万物皆为整数与整数之比的信条,并导致希帕索斯悲惨地死去,但该定理对数学的发展起到了巨大的促进作用。
?
????????????????????????????????????????????????????????????????????????????????????
(Pythagoras, 约公元前580~前500) 在西方最早发现这个定理的相传是公元前五百多年古希腊数学家毕达哥拉斯,所以西方称它“毕达哥拉斯定理”.abcaaabbbcccS正方形ABCD=(a+b)(a+b)=(a+b)2ACDBS正方形ABCD=+S小绿正方形4×S红直角三角形 图形经过割补拼接后,只要没有空隙,没有重叠,面积不会改变。∴ a2+b2=c2 图1称为“弦图”,最早是由三国时期(公元200年)的数学家赵爽在为《周髀算经》作注时给出的.图2是在北京召开的2002年国际数学家大会(ICM2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.
你可以根据这张”弦图”推出勾股定理吗?(1)(2)S正方形ABCD=
∴ a2+b2=c2试一试如图有两个一模一样的直角三角形,两直角边为a,b斜边为c,另一个大的是一个等腰直角三角形,直角边为c,请开动脑筋,把他拼成一个可以证明勾股定理的图形,
拼一拼美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法。 有趣的总统证法aabbccABCDE1.如图,受台风韦伯影响,一棵树在离地面4米处断裂, 树的顶部落在离树跟底部3米处,这棵树折断前有多高?应用知识回归生活应用知识回归生活王子救公主的故事营救方案小船能漂多远?4. 如图,为了求出湖两岸的AB两点之间的距离,一个观测者在点C设桩,使△ABC恰好为Rt△,通过测量,得到AC长160米,BC长128米,问从A点穿过湖到点B有多远?
解:Rt△ABC中,AC=160,BC=128,
根据勾股定理得:
答:从A点穿过湖到点B有96米。应用知识回归生活x5. 假期中,王强和同学到某海岛上去探宝旅游,按照探宝图(如图),他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A到宝藏埋藏点B的直线距离是多少千米?应用知识回归生活 做一个长,宽,高分别为50厘米,40厘米,30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明。练一练:30cm40cm50cm1图形经过割补拼接后,只要没有空隙,没有重叠,面积不会改变。小 结:2构造直角三角形,将实际问题转化为数学问题,
运用勾股定理建立方程求解。 作业:1.网上搜索有关勾股定理的其他证明(拼图),并结合自己的观 点完成一篇400字左右的论文.
2.完成书后的习题p53,练习1,2 毕达哥拉斯创建了政治、宗教、数学合一的秘密学术团体,这个团体被后人称为毕达哥拉斯学派。
这个学派的活动都是秘密的,笼罩着一种不可思议的神秘气氛。据说,每个新入学的学生都得宣誓严守秘密,并终身只加入这一学派。该学派还有一种习惯,就是将一切发明都归之于学派的领袖,而且秘而不宣,以致后人不知是何人在何时所发明的。
毕达哥拉斯定理(即勾股定理)是毕达哥拉斯的一大贡献,他的一个学生希帕索斯通过勾股定理发现了无理数,虽然这一发现打破了毕达哥拉斯宇宙万物皆为整数与整数之比的信条,并导致希帕索斯悲惨地死去,但该定理对数学的发展起到了巨大的促进作用。
