人教版数学八年级上册 14.1.4.3 多项式乘多项式 课件(共13张PPT)
文档属性
| 名称 | 人教版数学八年级上册 14.1.4.3 多项式乘多项式 课件(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-15 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
14.1.4.3多项式乘多项式
1、探索并了解多项式乘以多项式的法则。
2、灵活运用多项式乘以多项式的法则进行运算。
学 习 目 标
单项式与单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。
单项式与单项式相乘的法则:
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
单项式乘以多项式的法则:
p(a+b+c) =pa+pb+pc
复 习 导 入
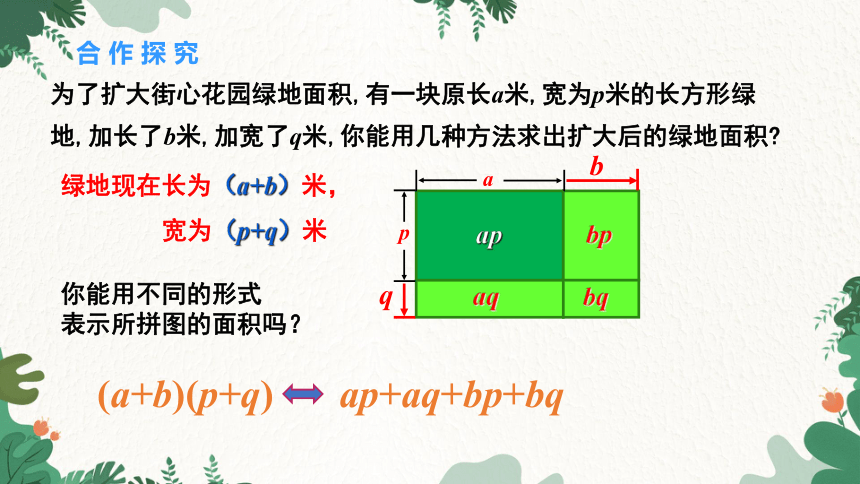
为了扩大街心花园绿地面积,有一块原长a米,宽为p米的长方形绿地,加长了b米,加宽了q米,你能用几种方法求出扩大后的绿地面积
p
a
q
b
aq
bq
ap
bp
你能用不同的形式
表示所拼图的面积吗?
绿地现在长为(a+b)米,
宽为(p+q)米
(a+b)(p+q)
ap+aq+bp+bq
合 作 探 究
(a+b)(p+q)=
= ap+aq+bp+bq
(a+b)看作一个整体
q(a+b)
p(a+b)
+
由单项式乘以多项式的法则,得
从整体看,(a+b)(p+q)的结果可以看作由多项式(a+b)的每一项乘以多项式(p+q)的每一项,再把所得的积相加而得到的。
(a+b)( p+q)=
+aq
ap
+bp
+bq
先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
多项式乘以多项式
(a+b)(m+n)
=
am
+an
+bm
+bn
1
1
2
2
3
3
4
4
新 知 小 结
( 1 )( 3x+1 ) (x+2)
( 3 ) (x+y)(x2 -xy+ y2).
( 2 ) (x-8y)(x - y).
解: (1) 原式=3x×x+2×3x+1×x+1×2
(2) 原式=x·x-xy-8xy+8y2
结果中有同类项的要合并同类项.
=3x2+7x+2;
计算时要注意符号问题.
=x2-9xy+8y2;
=3x2+6x+x+2
计算:
典 例 精 析
=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
= x3+y3.
( 3 )解: (x+y)(x2 -xy+ y2).
(1)必须做到不重复,不漏乘;
(2)符号问题:确定积中每一项的符号;
(3)最后结果应化成最简形式.
多项式与多项式相乘应注意的几个问题:
1.计算(x-2)(x-3)的结果为( )
A.x2+5x-6 B.x2-5x-6
C.x2+5x+6 D.x2-5x+6
D
2.下列多项式相乘,结果为x2-3x-4的是( )
A.(x-1)(x+4) B.(x-4)(x+1)
C.(x-1)(x-4) D.(x+1)(x-4)
D
随 堂 练 习
3.计算(a﹣2)(a+3)的结果是( )
A.a2﹣6 B.a2+a﹣6 C.a2+6 D.a2﹣a+6
4.如果(x-3)(x+4)=x2+px+q,那么p,q的值是( )
A.p=1,q=﹣12 B.p=﹣1,q=12
C.p=7,q=12 D.p=7,q=﹣12
B
A
5. 已知ax2+2bx+2(a≠0)与x-1的积不含x2项,也不含x项,求系数a、b的值.
解:(ax2+2bx+2)(x-1)
=ax3-ax2+2bx2-2bx+2x-2,
∵积不含x2的项,也不含x的项,
-a+2b=0
-2b+2=0
∴
解得
a=2
b=1
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
多项式与多项式相乘的法则:
(1)必须做到不重复,不漏乘;
(2)符号问题:确定积中每一项的符号;
(3)最后结果应化成最简形式.
多项式与多项式相乘应注意的几个问题:
课 堂 总 结
谢谢大家!
14.1.4.3多项式乘多项式
1、探索并了解多项式乘以多项式的法则。
2、灵活运用多项式乘以多项式的法则进行运算。
学 习 目 标
单项式与单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。
单项式与单项式相乘的法则:
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
单项式乘以多项式的法则:
p(a+b+c) =pa+pb+pc
复 习 导 入
为了扩大街心花园绿地面积,有一块原长a米,宽为p米的长方形绿地,加长了b米,加宽了q米,你能用几种方法求出扩大后的绿地面积
p
a
q
b
aq
bq
ap
bp
你能用不同的形式
表示所拼图的面积吗?
绿地现在长为(a+b)米,
宽为(p+q)米
(a+b)(p+q)
ap+aq+bp+bq
合 作 探 究
(a+b)(p+q)=
= ap+aq+bp+bq
(a+b)看作一个整体
q(a+b)
p(a+b)
+
由单项式乘以多项式的法则,得
从整体看,(a+b)(p+q)的结果可以看作由多项式(a+b)的每一项乘以多项式(p+q)的每一项,再把所得的积相加而得到的。
(a+b)( p+q)=
+aq
ap
+bp
+bq
先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
多项式乘以多项式
(a+b)(m+n)
=
am
+an
+bm
+bn
1
1
2
2
3
3
4
4
新 知 小 结
( 1 )( 3x+1 ) (x+2)
( 3 ) (x+y)(x2 -xy+ y2).
( 2 ) (x-8y)(x - y).
解: (1) 原式=3x×x+2×3x+1×x+1×2
(2) 原式=x·x-xy-8xy+8y2
结果中有同类项的要合并同类项.
=3x2+7x+2;
计算时要注意符号问题.
=x2-9xy+8y2;
=3x2+6x+x+2
计算:
典 例 精 析
=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
= x3+y3.
( 3 )解: (x+y)(x2 -xy+ y2).
(1)必须做到不重复,不漏乘;
(2)符号问题:确定积中每一项的符号;
(3)最后结果应化成最简形式.
多项式与多项式相乘应注意的几个问题:
1.计算(x-2)(x-3)的结果为( )
A.x2+5x-6 B.x2-5x-6
C.x2+5x+6 D.x2-5x+6
D
2.下列多项式相乘,结果为x2-3x-4的是( )
A.(x-1)(x+4) B.(x-4)(x+1)
C.(x-1)(x-4) D.(x+1)(x-4)
D
随 堂 练 习
3.计算(a﹣2)(a+3)的结果是( )
A.a2﹣6 B.a2+a﹣6 C.a2+6 D.a2﹣a+6
4.如果(x-3)(x+4)=x2+px+q,那么p,q的值是( )
A.p=1,q=﹣12 B.p=﹣1,q=12
C.p=7,q=12 D.p=7,q=﹣12
B
A
5. 已知ax2+2bx+2(a≠0)与x-1的积不含x2项,也不含x项,求系数a、b的值.
解:(ax2+2bx+2)(x-1)
=ax3-ax2+2bx2-2bx+2x-2,
∵积不含x2的项,也不含x的项,
-a+2b=0
-2b+2=0
∴
解得
a=2
b=1
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
多项式与多项式相乘的法则:
(1)必须做到不重复,不漏乘;
(2)符号问题:确定积中每一项的符号;
(3)最后结果应化成最简形式.
多项式与多项式相乘应注意的几个问题:
课 堂 总 结
谢谢大家!
