人教版数学八年级上册 11.1.3 三角形的稳定性课件 (共14张PPT)
文档属性
| 名称 | 人教版数学八年级上册 11.1.3 三角形的稳定性课件 (共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-15 14:39:21 | ||
图片预览






文档简介
(共14张PPT)
11.1.3 三角形的稳定性
1.通过实践活动,进一步掌握三角形的稳定性.
2.学会从生活中发现数学问题,运用所学知识解决实际问题的能力.从而体验到数学与日常生活的密切联系.
观察上面这些物体,你发现了什么?
将三根木条用钉子钉成一个三角形木架.
将四根木条用钉子钉成一个四边形木架.
新知一 三角形的稳定性
动手做一做
(1)扭动这个三角形木架,你能发现什么
(2)扭动这个四边形木架,你能发现什么
三角形木架形状不会改变
四边形木架形状会改变
(3)在四边形木架上斜钉一根木条后扭动它,
四边形木架的形状还会不会发生变化?
斜钉一根木条后,四边形被分割成成两个三角形,由于三角形具有稳定性,所以现在四边形木架的形状不会发生改变.
从上面实验过程你能得出什么结论?
三角形具有稳定性,四边形具有不稳定性.
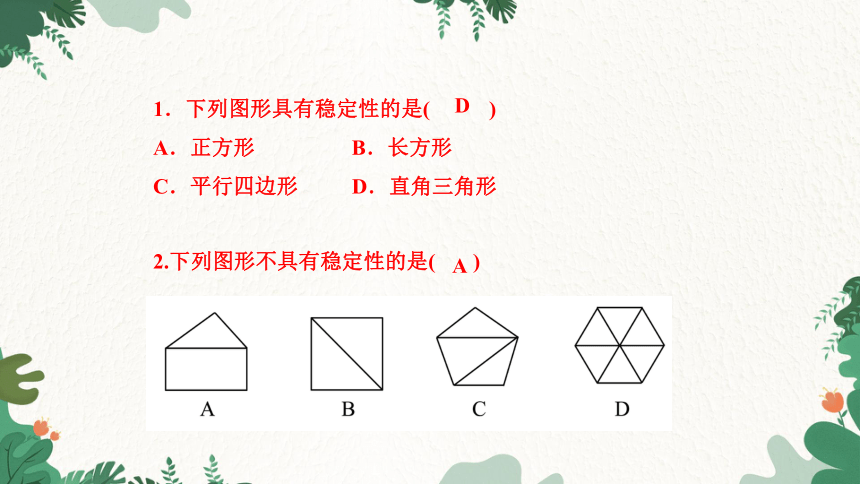
1.下列图形具有稳定性的是( )
A.正方形 B.长方形
C.平行四边形 D.直角三角形
D
2.下列图形不具有稳定性的是( )
A
只要三角形三条边的长度固定,这个三角形的形状和大小也就完全确定,三角形的这种性质叫做三角形的稳定性.
【思考】你能举出一些现实生活中应用三角形稳定性的例子吗
什么是三角形的稳定性
想一想:
四边形的不稳定性是我们常常需要克服的,那么四边形的不稳定性在生活中有没有应用价值呢?如果有,你能举出实例吗?
新知二 四边形不稳定性的应用
伸缩晾衣架
伸缩门
折叠遮阳棚
图 1
图 2
例1 (1)小明家的一段栅栏由于疏于维护,形状已经变成如图1所示,
为什么会变形?
(2)小明修复了栅栏,如图2所示.要保持栅栏形状不再变化,
他该怎么做呢?
答:(1)栅栏是四边形,四边形具有不稳定性
(2)如图2,斜钉一根木条
例2 右图是一个天线支架的示意图,上方横梁容易转动,
怎样做可以使它稳定
我们已经知道了:四边形具有不稳定性,要使四边形木架不变形,至少要钉上一根木条,把它分成两个三角形;
那么五边形、六边形、七边形具有稳定性吗?如果不,怎样才能使它们稳定?
方法总结:为了使多边形具有稳定性,一般需要用木条将多边形固定成由一个一个的三角形组成的形式.
1.在建筑工地我们常可看见如图所示,用木条EF固定
矩形门框ABCD的情形.这种做法的根据( ).
A.两点之间线段 B.两点确定一条直线
C.三角形的稳定性 D.矩形的四个角都是直角
C
2.下列图中具有稳定性有( )
A. 1个 B. 2个 C. 3个 D. 4个
C
三角形的稳定性
三角形的稳定性在生活中的应用;
四边形的不稳定性在生活中的应用;
四边形不稳定性的克服
谢谢大家!
11.1.3 三角形的稳定性
1.通过实践活动,进一步掌握三角形的稳定性.
2.学会从生活中发现数学问题,运用所学知识解决实际问题的能力.从而体验到数学与日常生活的密切联系.
观察上面这些物体,你发现了什么?
将三根木条用钉子钉成一个三角形木架.
将四根木条用钉子钉成一个四边形木架.
新知一 三角形的稳定性
动手做一做
(1)扭动这个三角形木架,你能发现什么
(2)扭动这个四边形木架,你能发现什么
三角形木架形状不会改变
四边形木架形状会改变
(3)在四边形木架上斜钉一根木条后扭动它,
四边形木架的形状还会不会发生变化?
斜钉一根木条后,四边形被分割成成两个三角形,由于三角形具有稳定性,所以现在四边形木架的形状不会发生改变.
从上面实验过程你能得出什么结论?
三角形具有稳定性,四边形具有不稳定性.
1.下列图形具有稳定性的是( )
A.正方形 B.长方形
C.平行四边形 D.直角三角形
D
2.下列图形不具有稳定性的是( )
A
只要三角形三条边的长度固定,这个三角形的形状和大小也就完全确定,三角形的这种性质叫做三角形的稳定性.
【思考】你能举出一些现实生活中应用三角形稳定性的例子吗
什么是三角形的稳定性
想一想:
四边形的不稳定性是我们常常需要克服的,那么四边形的不稳定性在生活中有没有应用价值呢?如果有,你能举出实例吗?
新知二 四边形不稳定性的应用
伸缩晾衣架
伸缩门
折叠遮阳棚
图 1
图 2
例1 (1)小明家的一段栅栏由于疏于维护,形状已经变成如图1所示,
为什么会变形?
(2)小明修复了栅栏,如图2所示.要保持栅栏形状不再变化,
他该怎么做呢?
答:(1)栅栏是四边形,四边形具有不稳定性
(2)如图2,斜钉一根木条
例2 右图是一个天线支架的示意图,上方横梁容易转动,
怎样做可以使它稳定
我们已经知道了:四边形具有不稳定性,要使四边形木架不变形,至少要钉上一根木条,把它分成两个三角形;
那么五边形、六边形、七边形具有稳定性吗?如果不,怎样才能使它们稳定?
方法总结:为了使多边形具有稳定性,一般需要用木条将多边形固定成由一个一个的三角形组成的形式.
1.在建筑工地我们常可看见如图所示,用木条EF固定
矩形门框ABCD的情形.这种做法的根据( ).
A.两点之间线段 B.两点确定一条直线
C.三角形的稳定性 D.矩形的四个角都是直角
C
2.下列图中具有稳定性有( )
A. 1个 B. 2个 C. 3个 D. 4个
C
三角形的稳定性
三角形的稳定性在生活中的应用;
四边形的不稳定性在生活中的应用;
四边形不稳定性的克服
谢谢大家!
