镶嵌(浙江省台州市)
图片预览







文档简介
课件39张PPT。1、请各组长将信封内的材料取出,
按类分好,放在桌面上。
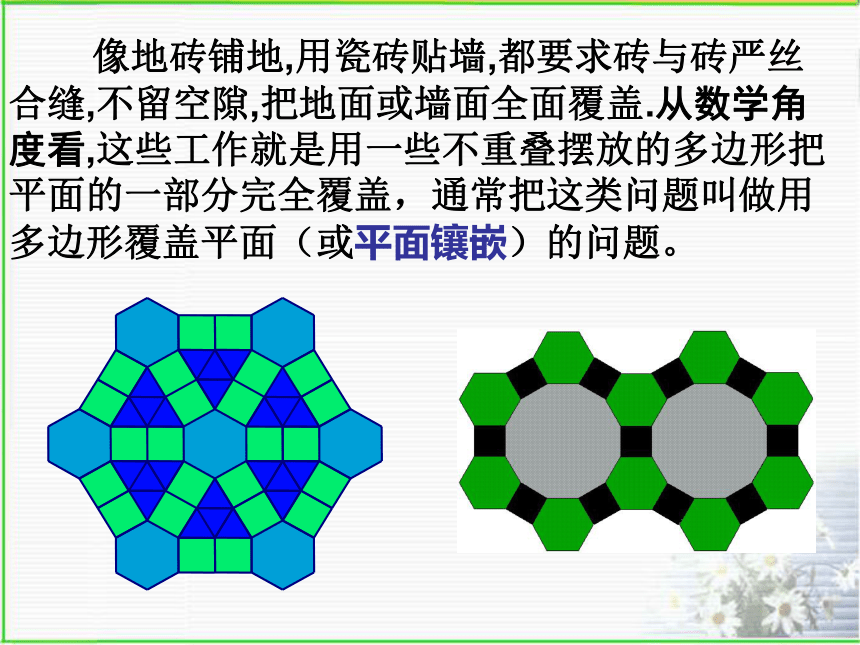
2、材料有点瑕疵,还望各位同学谅解!7.4课题学习:镶嵌 像地砖铺地,用瓷砖贴墙,都要求砖与砖严丝合缝,不留空隙,把地面或墙面全面覆盖.从数学角度看,这些工作就是用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做用多边形覆盖平面(或平面镶嵌)的问题。
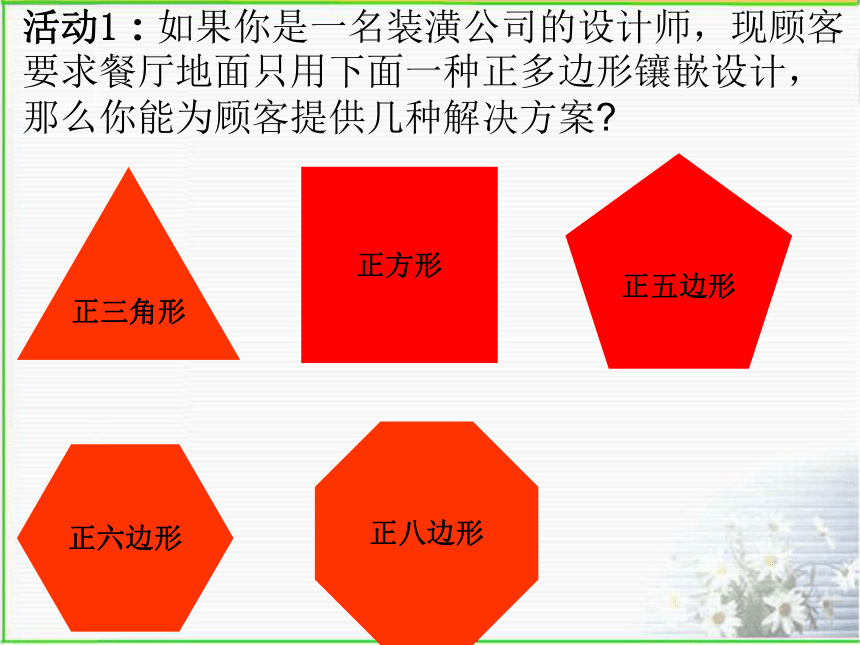
活动1:如果你是一名装潢公司的设计师,现顾客要求餐厅地面只用下面一种正多边形镶嵌设计,那么你能为顾客提供几种解决方案?正三角形正方形正五边形正六边形正八边形64334能镶嵌能镶嵌不能镶嵌
有空隙能镶嵌108°×3<360°不能镶嵌
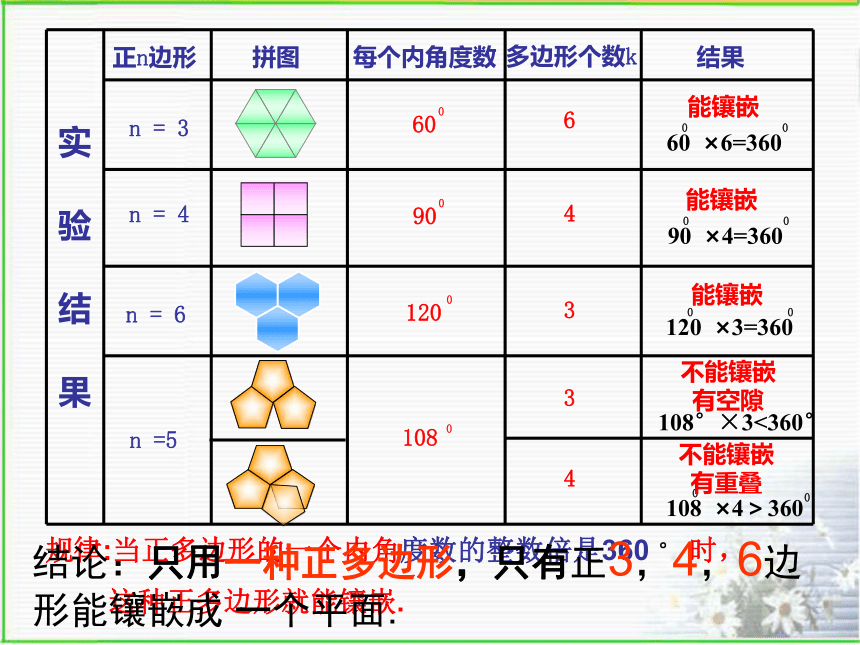
有重叠实 验 结 果正n边形拼图每个内角度数多边形个数k结果 n = 3 n = 4 n =5 n = 6规律:当正多边形的一个内角度数的整数倍是360 ° 时,
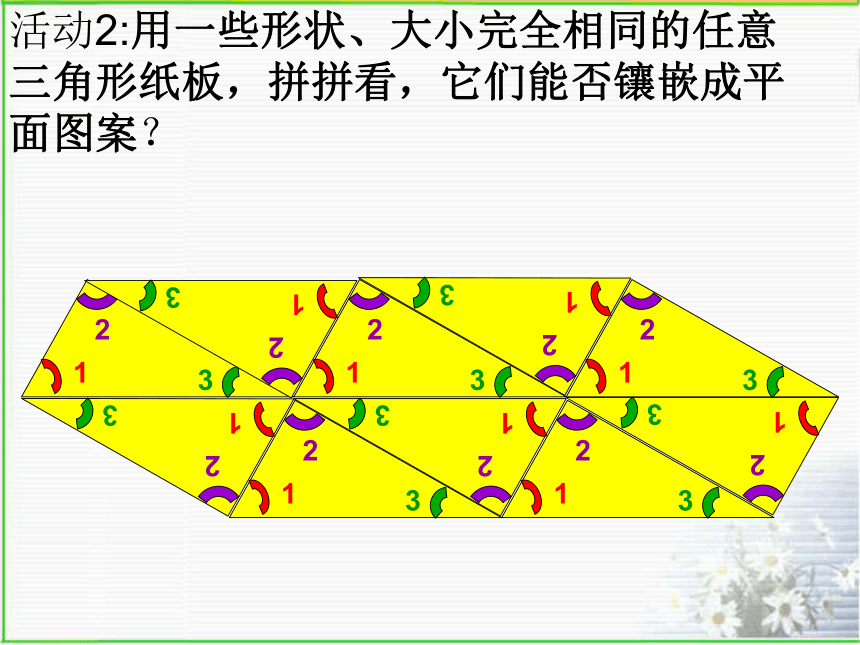
这种正多边形就能镶嵌.结论:只用一种正多边形,只有正3,4,6边形能镶嵌成 一个平面.活动2:用一些形状、大小完全相同的任意三角形纸板,拼拼看,它们能否镶嵌成平面图案?
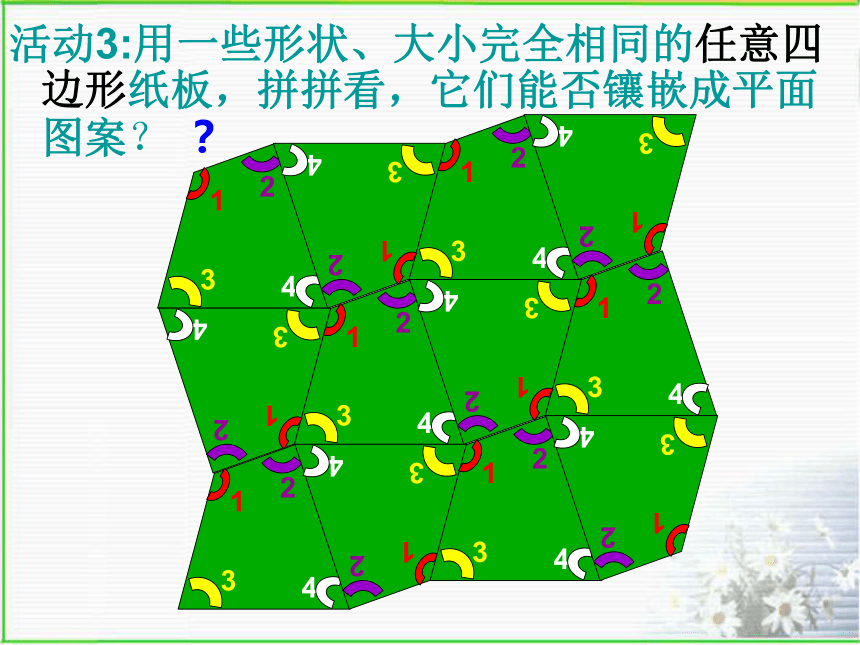
活动3:用一些形状、大小完全相同的任意四边形纸板,拼拼看,它们能否镶嵌成平面图案? ? 归纳:1、任意三角形一定可以镶嵌. 3、 正六边形可以镶嵌. 2、任意四边形一定可以镶嵌圣地亚哥人玛乔里·赖斯
于1977年12月发现. 如果你是一名装潢公司的设计师,现顾客要求客厅用正三角形、正方形中的两种正多边形镶嵌设计地面,那么你能为顾客提供设计方案?
正三角形与正方形
活动4:如果你是一名装潢公司的设计师,现顾客要求客厅用正三角形、正方形、正五边形、正六边形、正八边形中的两种正多边形镶嵌设计地面,那么你能为顾客提供几种设计方案?正三角形与正方形正六边形和正三角形正四边形与正八边形
结论平面镶嵌的必备条件: 图形拼合后,同一个顶点的
几个角的和等于360度.利用镶嵌可以得到一些绚丽多彩的图案我们要学会欣赏美,
更会用数学去创造美!镶嵌之父M.C.埃舍尔是荷兰的“图形艺术家”,
着迷于各种镶嵌。许多数学家认为在他的作
品中数学的原则和思想得到了非同寻常的形
象化。他的作品几乎无人能够企及,世人尊
称他为“镶嵌之父”。 。无论这个问题从属于数学领域还是从属于
艺术领域,它对于我仍然是一个未解的问题。
——M.C.埃舍尔 通过本节课的探究
我经历了……
我体会了……
我感受了……
我学会了……谢 谢!108o108o108o36o135o90o135o1.由正三角形与正方形2.由正三角形与正六边形3.由正方形与正八边形
按类分好,放在桌面上。
2、材料有点瑕疵,还望各位同学谅解!7.4课题学习:镶嵌 像地砖铺地,用瓷砖贴墙,都要求砖与砖严丝合缝,不留空隙,把地面或墙面全面覆盖.从数学角度看,这些工作就是用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做用多边形覆盖平面(或平面镶嵌)的问题。
活动1:如果你是一名装潢公司的设计师,现顾客要求餐厅地面只用下面一种正多边形镶嵌设计,那么你能为顾客提供几种解决方案?正三角形正方形正五边形正六边形正八边形64334能镶嵌能镶嵌不能镶嵌
有空隙能镶嵌108°×3<360°不能镶嵌
有重叠实 验 结 果正n边形拼图每个内角度数多边形个数k结果 n = 3 n = 4 n =5 n = 6规律:当正多边形的一个内角度数的整数倍是360 ° 时,
这种正多边形就能镶嵌.结论:只用一种正多边形,只有正3,4,6边形能镶嵌成 一个平面.活动2:用一些形状、大小完全相同的任意三角形纸板,拼拼看,它们能否镶嵌成平面图案?
活动3:用一些形状、大小完全相同的任意四边形纸板,拼拼看,它们能否镶嵌成平面图案? ? 归纳:1、任意三角形一定可以镶嵌. 3、 正六边形可以镶嵌. 2、任意四边形一定可以镶嵌圣地亚哥人玛乔里·赖斯
于1977年12月发现. 如果你是一名装潢公司的设计师,现顾客要求客厅用正三角形、正方形中的两种正多边形镶嵌设计地面,那么你能为顾客提供设计方案?
正三角形与正方形
活动4:如果你是一名装潢公司的设计师,现顾客要求客厅用正三角形、正方形、正五边形、正六边形、正八边形中的两种正多边形镶嵌设计地面,那么你能为顾客提供几种设计方案?正三角形与正方形正六边形和正三角形正四边形与正八边形
结论平面镶嵌的必备条件: 图形拼合后,同一个顶点的
几个角的和等于360度.利用镶嵌可以得到一些绚丽多彩的图案我们要学会欣赏美,
更会用数学去创造美!镶嵌之父M.C.埃舍尔是荷兰的“图形艺术家”,
着迷于各种镶嵌。许多数学家认为在他的作
品中数学的原则和思想得到了非同寻常的形
象化。他的作品几乎无人能够企及,世人尊
称他为“镶嵌之父”。 。无论这个问题从属于数学领域还是从属于
艺术领域,它对于我仍然是一个未解的问题。
——M.C.埃舍尔 通过本节课的探究
我经历了……
我体会了……
我感受了……
我学会了……谢 谢!108o108o108o36o135o90o135o1.由正三角形与正方形2.由正三角形与正六边形3.由正方形与正八边形
