2023-2024学年苏科版数学七年级上册 2.8 有理数的混合运算 同步练习(含解析)
文档属性
| 名称 | 2023-2024学年苏科版数学七年级上册 2.8 有理数的混合运算 同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 169.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-15 18:09:06 | ||
图片预览




文档简介
2.8有理数的混合运算
一.选择题(共8小题)
1.下列四个算式:①﹣2﹣3=﹣5;②2﹣|﹣3|=﹣1;③(﹣2)3=﹣6;④﹣2÷13=-6,其中正确的算式有( )
A.0个 B.1个 C.2个 D.3个
2.计算48÷(815+2435)之值为何( )
A.75 B.160 C.3158 D.902435
3.如果a、b互为相反数,c、d互为倒数,x的绝对值等于2,那么cdx2﹣a﹣b的值是( )
A.4 B.﹣4 C.4或﹣4 D.无法确定
4.在数学课上,老师让甲、乙、丙、丁,四位同学分别做了一道有理数运算题,你认为做对的同学是( )
甲:9﹣32÷8=0÷8=0
乙:24﹣(4×32)=24﹣4×6=0
丙:(36﹣12)÷32=36×23-12×23=16
丁:(﹣3)2÷13×3=9÷1=9
A.甲 B.乙 C.丙 D.丁
5.如图是一个数值运算的程序,若输出的y值为3,则输入的x值为( )
A.3.5 B.﹣3.5 C.7 D.﹣7
6.已知某快递公司的收费标准为:寄一件物品不超过5千克,收费13元;超过5千克的部分每千克加收2元.圆圆在该快递公司寄一件8千克的物品,需要付费( )
A.17元 B.19元 C.21元 D.23元
7.计算(﹣2)1999+(﹣2)2000的结果是( )
A.﹣21999 B.21999 C.﹣2 D.2
8.若“!”是一种运算符号,且1!=1,2!=2×1,3!=3×2×1,4!=4×3×2×1,…,则计算2008!2007!正确的是( )
A.2008 B.2007 C.20082007 D.2008×2007
二.填空题(共8小题)
9.(-12)3﹣1的值为 .
10.如图所示是计算机某计算程序,若开始输入x=3,则最后输出的结果是 .
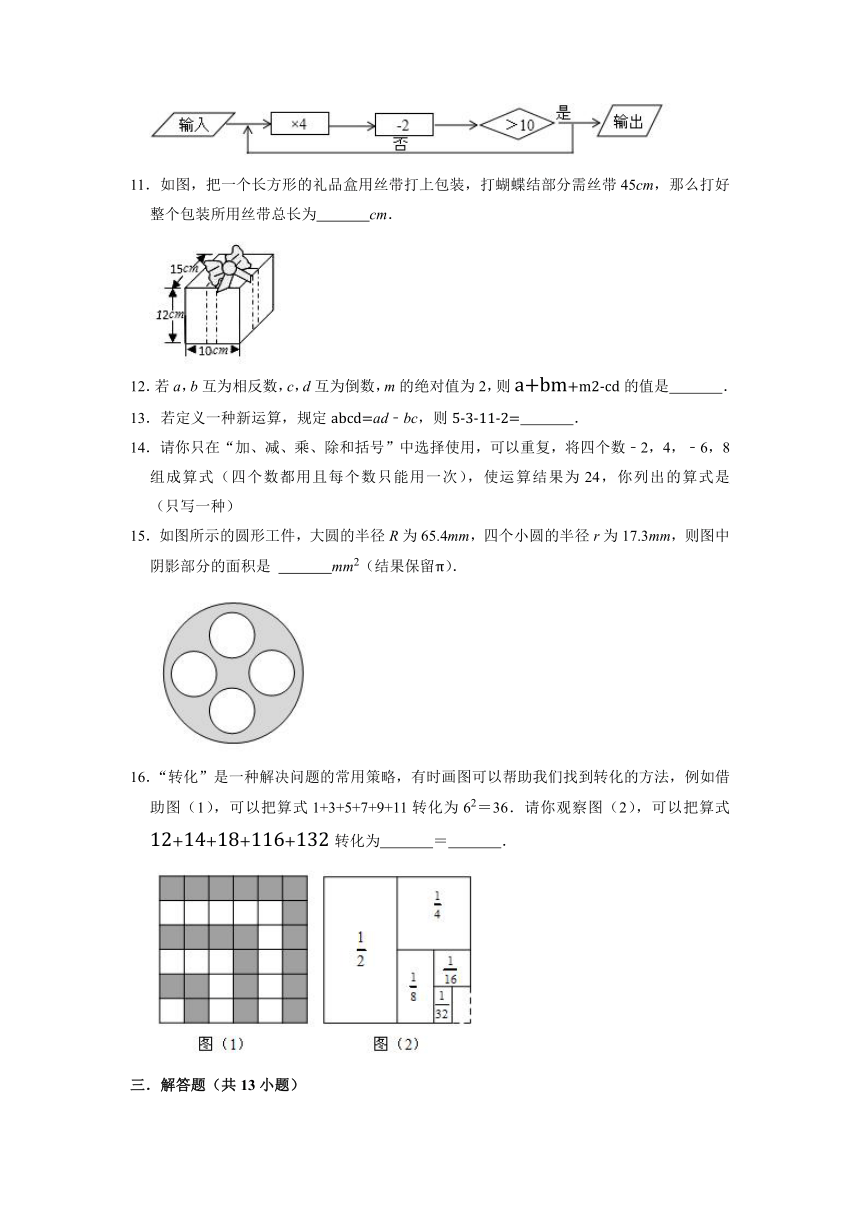
11.如图,把一个长方形的礼品盒用丝带打上包装,打蝴蝶结部分需丝带45cm,那么打好整个包装所用丝带总长为 cm.
12.若a,b互为相反数,c,d互为倒数,m的绝对值为2,则a+bm+m2-cd的值是 .
13.若定义一种新运算,规定abcd=ad﹣bc,则5-3-11-2= .
14.请你只在“加、减、乘、除和括号”中选择使用,可以重复,将四个数﹣2,4,﹣6,8组成算式(四个数都用且每个数只能用一次),使运算结果为24,你列出的算式是 (只写一种)
15.如图所示的圆形工件,大圆的半径R为65.4mm,四个小圆的半径r为17.3mm,则图中阴影部分的面积是 mm2(结果保留π).
16.“转化”是一种解决问题的常用策略,有时画图可以帮助我们找到转化的方法,例如借助图(1),可以把算式1+3+5+7+9+11转化为62=36.请你观察图(2),可以把算式12+14+18+116+132转化为 = .
三.解答题(共13小题)
17.计算
(1)27﹣18+(﹣7)﹣32;
(2)(-7)÷(-34)×(-43);
(3)(-34-56+78)×(-24);
(4)-14-16×[2-(-3)2].
18.已知:a,b互为相反数,c,d互为倒数,x的绝对值是2,求x2﹣(a+b+cd)x+(a+b)2011+(﹣cd)2012的值.
19.对于有理数a、b,定义一种新运算“⊙”,规定:a⊙b=|a+b|+|a﹣b|.
(1)计算2⊙(﹣4)的值;
(2)若a,b在数轴上的位置如图所示,化简a⊙b.
20.阅读下面的解题过程:
计算(﹣15)÷(13-12)×6
解:原式=(﹣15)÷(-16)×6(第一步)
=(﹣15)÷(﹣1)(第二步)
=﹣15(第三步)
回答:(1)上面解题过程中有两处错误,第一处是第 步,错误的原因是 ,第二处是第 步,错误的原因是 .
(2)把正确的解题过程写出来.
21.计算:(-130)÷(23-110+16-25)
解法1:原式=(-130)÷[(23+16)+(-110-25)]=(-130)÷(56-12)=-130×3=-110
解法2:原式的倒数为:(23-110+16-25)÷(-130)=(23-110+16-25)×(﹣30)=23×(﹣30)-110×(﹣30)+16×(﹣30)-25×(﹣30)=﹣20+3﹣5+12=﹣10
故原式=-110
请阅读上述材料,选择合适的方法计算:(-142)÷(16-314+23-27)
22.我国约有9.6×106平方千米的土地,平均1平方千米的土地一年从太阳得到的能相当于燃烧1.5×105吨煤所产生的能量
(1)一年内我国土地从太阳得到的能量相当于燃烧多少吨煤?(用科学记数法表示)
(2)若1吨煤大约可以发出8×103度电,那么(1)中的煤大约发出多少度电?(用科学记数法表示)
23.某粮库6天内粮食进、出库的吨数如下(“+”表示进库,“﹣”表示出库):
+26,﹣32,﹣15,+34,﹣38,﹣20
(1)经过这6天,仓库里的粮食是增加了还是减少了?
(2)经过这6天,仓库管理员结算时发现库里还存280吨粮,那么6天前仓库里存粮多少吨?
(3)如果进出的装卸费都是每吨5元,那么这6天要付多少装卸费?
24.已知某粮库已存有粮食100吨,本周内粮库进出粮食的记录如下(运进为正):
星期 一 二 三 四 五 六 日
进、出记录 +35 ﹣20 ﹣30 +25 ﹣24 +50 ﹣26
(1)通过计算,说明本周内哪天粮库剩余的粮食最多?
(2)若运进的粮食为购进的,购买价格为每吨2000元,运出的粮食为卖出的,卖出的价格为每吨2300元,则这一周的利润为多少?
(3)若每周平均进出的粮食大致相同,则再过几周粮库存的粮食可达到200吨?
25.小明爸爸给小明出了一道题,说明他本月炒股的盈亏情况(单位:元)
股票 每股净赚(元) 股票
招商银行 +23 500
浙江医药 ﹣(﹣2.8) 1000
晨光文具 ﹣1.5 1500
金龙汽车 ﹣145 2000
请你也来计算一下,小明爸爸本月投资炒股到底是赔了还是赚了?赔了或赚了多少元?
26.某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如下(规定向南为正,向北为负,单位:km):
第1批 第2批 第3批 第4批 第5批
5km 2km ﹣4km ﹣3km 10km
(1)接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
(3)若该出租车的计价标准为:行驶路程不超过3km收费10元,超过3km的部分按每千米加1.8元收费,在这过程中该驾驶员共收到车费多少元?
27.在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.
(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;
(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.
28.阅读下列材料:|x|=x,x>00,x=0-x,x<0,即当x<0时,x|x|=x-x=-1.用这个结论可以解决下面问题:
(1)已知a,b是有理数,当ab≠0时,求a|a|+b|b|的值;
(2)已知a,b,c是有理数,当abc≠0时,求a|a|+b|b|+c|c|的值;
(3)已知a,b,c是有理数,a+b+c=0,abc<0,求b+c|a|+a+c|b|+a+b|c|的值.
29.如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(结果保留π)
(1)把圆片沿数轴向左滚动1周,点A到达数轴上点C的位置,点C表示的数是 数(填“无理”或“有理”),这个数是 ;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是 ;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3.第几次滚动后,A点距离原点最近?第几次滚动后,A点距离原点最远?
2.8有理数的混合运算同步练习(基础版解析)
一.选择题(共8小题)
1.下列四个算式:①﹣2﹣3=﹣5;②2﹣|﹣3|=﹣1;③(﹣2)3=﹣6;④﹣2÷13=-6,其中正确的算式有( )
A.0个 B.1个 C.2个 D.3个
【解答】解:①﹣2﹣3=﹣5,正确;
②2﹣|﹣3|=2﹣3=﹣1,正确;
③(﹣2)3=﹣8,原来的计算错误;
④﹣2÷13=-6,正确.
故其中正确的算式有3个.
故选:D.
2.计算48÷(815+2435)之值为何( )
A.75 B.160 C.3158 D.902435
【解答】解:48÷(815+2435),
=48÷(8×715×7+24×335×3),
=48÷128105,
=48×105128,
=3158.
故选:C.
3.如果a、b互为相反数,c、d互为倒数,x的绝对值等于2,那么cdx2﹣a﹣b的值是( )
A.4 B.﹣4 C.4或﹣4 D.无法确定
【解答】解:∵a、b互为相反数,c、d互为倒数,x的绝对值等于2,
∴a+b=0,cd=1,|x|=2,
∴cdx2﹣a﹣b
=1×22﹣0
=4﹣0
=4.
故选:A.
4.在数学课上,老师让甲、乙、丙、丁,四位同学分别做了一道有理数运算题,你认为做对的同学是( )
甲:9﹣32÷8=0÷8=0
乙:24﹣(4×32)=24﹣4×6=0
丙:(36﹣12)÷32=36×23-12×23=16
丁:(﹣3)2÷13×3=9÷1=9
A.甲 B.乙 C.丙 D.丁
【解答】解:甲:9﹣32÷8=9﹣9÷8=778,原来没有做对;
乙:24﹣(4×32)=24﹣4×9=﹣12,原来没有做对;
丙:(36﹣12)÷32=36×23-12×23=16,做对了;
丁:(﹣3)2÷13×3=9÷13×3=81,原来没有做对.
故选:C.
5.如图是一个数值运算的程序,若输出的y值为3,则输入的x值为( )
A.3.5 B.﹣3.5 C.7 D.﹣7
【解答】解:由题意可得,
[(﹣x)﹣1]÷2=y,
当y=3时,
[(﹣x)﹣1]÷2=3,
解得,x=﹣7,
故选:D.
6.已知某快递公司的收费标准为:寄一件物品不超过5千克,收费13元;超过5千克的部分每千克加收2元.圆圆在该快递公司寄一件8千克的物品,需要付费( )
A.17元 B.19元 C.21元 D.23元
【解答】解:根据题意得:13+(8﹣5)×2=13+6=19(元).
则需要付费19元.
故选:B.
7.计算(﹣2)1999+(﹣2)2000的结果是( )
A.﹣21999 B.21999 C.﹣2 D.2
【解答】解:(﹣2)1999+(﹣2)2000
=2×21999﹣21999
=21999(2﹣1)
=21999.
故选:B.
8.若“!”是一种运算符号,且1!=1,2!=2×1,3!=3×2×1,4!=4×3×2×1,…,则计算2008!2007!正确的是( )
A.2008 B.2007 C.20082007 D.2008×2007
【解答】解:2008!2007!=2008×2007×2006× ×12007×2006× ×1=2008.
故选:A.
二.填空题(共8小题)
9.(-12)3﹣1的值为 -118 .
【解答】解:(-12)3﹣1
=-18-1
=﹣118.
故答案为:﹣118.
10.如图所示是计算机某计算程序,若开始输入x=3,则最后输出的结果是 38 .
【解答】解:根据题意可知,3×4﹣2=10=10,
所以再把10代入计算:10×4﹣2=38>10,
即38为最后结果.
故本题答案为:38.
11.如图,把一个长方形的礼品盒用丝带打上包装,打蝴蝶结部分需丝带45cm,那么打好整个包装所用丝带总长为 143 cm.
【解答】解:2×10+2×15+4×12+45=143cm.故填143.
12.若a,b互为相反数,c,d互为倒数,m的绝对值为2,则a+bm+m2-cd的值是 3 .
【解答】解:∵a,b互为相反数,c,d互为倒数,m的绝对值为2,
∴a+b=0,cd=1,|m|=2,
∴m2=4,
若m=2,则a+bm+m2-cd=02+4﹣1=3,
若m=﹣2,则a+bm+m2-cd=0-2+4﹣1=3,
∴a+bm+m2-cd=3.
故答案为:3.
13.若定义一种新运算,规定abcd=ad﹣bc,则5-3-11-2= ﹣43 .
【解答】解:∵abcd=ad﹣bc,
∴5-3-11-2
=5×(﹣2)﹣(﹣3)×(﹣11)
=﹣10﹣33
=﹣43.
故答案为:﹣43.
14.请你只在“加、减、乘、除和括号”中选择使用,可以重复,将四个数﹣2,4,﹣6,8组成算式(四个数都用且每个数只能用一次),使运算结果为24,你列出的算式是 8×(﹣6)÷[4÷(﹣2)]=24 (只写一种)
【解答】解:8×(﹣6)÷[4÷(﹣2)]=24
故答案为:8×(﹣6)÷[4÷(﹣2)]=24.(答案不唯一)
15.如图所示的圆形工件,大圆的半径R为65.4mm,四个小圆的半径r为17.3mm,则图中阴影部分的面积是 3080π mm2(结果保留π).
【解答】解:S阴影=S大圆﹣4S小圆
=πR2﹣4πr2=π(R2﹣4r2)
=π(R+2r)(R﹣2r)
=π(65.4+34.6)(65.4﹣34.6)
=3080π.
故答案为3080πmm2.
16.“转化”是一种解决问题的常用策略,有时画图可以帮助我们找到转化的方法,例如借助图(1),可以把算式1+3+5+7+9+11转化为62=36.请你观察图(2),可以把算式12+14+18+116+132转化为 1-132 = 3132 .
【解答】解:观察图(2),可以把算式12+14+18+116+132转化为 1-132=3132.
故答案为:1-132,3132.
三.解答题(共13小题)
17.计算
(1)27﹣18+(﹣7)﹣32;
(2)(-7)÷(-34)×(-43);
(3)(-34-56+78)×(-24);
(4)-14-16×[2-(-3)2].
【解答】解:(1)27﹣18+(﹣7)﹣32
=27﹣18﹣7﹣32
=27﹣57
=﹣30;
(2)(-7)÷(-34)×(-43)
=﹣7×43×43
=-1129;
(3)(-34-56+78)×(-24)
=-34×(﹣24)-56×(﹣24)+78×(﹣24)
=18+20﹣21
=17;
(4)-14-16×[2-(-3)2]
=﹣1-16×(2﹣9)
=﹣1-16×(﹣7)
=﹣1+76
=16.
18.已知:a,b互为相反数,c,d互为倒数,x的绝对值是2,求x2﹣(a+b+cd)x+(a+b)2011+(﹣cd)2012的值.
【解答】解:由已知可得,a+b=0,cd=1,x=±2;
当x=2时,
x2﹣(a+b+cd)x+(a+b)2011+(﹣cd)2012
=22﹣(0+1)×2+02011+(﹣1)2012
=4﹣2+0+1
=3
当x=﹣2时,
x2﹣(a+b+cd)x+(a+b)2011+(﹣cd)2012
=(﹣2)2﹣(0+1)×(﹣2)+02011+(﹣1)2012
=4+2+0+1
=7
19.对于有理数a、b,定义一种新运算“⊙”,规定:a⊙b=|a+b|+|a﹣b|.
(1)计算2⊙(﹣4)的值;
(2)若a,b在数轴上的位置如图所示,化简a⊙b.
【解答】解:(1)2⊙(﹣4)=|2﹣4|+|2+4|=2+6=8;
(2)由数轴知a<0<b,且|a|>|b|,
则a+b<0、a﹣b<0,
所以原式=﹣(a+b)﹣(a﹣b)
=﹣a﹣b﹣a+b
=﹣2a.
20.阅读下面的解题过程:
计算(﹣15)÷(13-12)×6
解:原式=(﹣15)÷(-16)×6(第一步)
=(﹣15)÷(﹣1)(第二步)
=﹣15(第三步)
回答:(1)上面解题过程中有两处错误,第一处是第 二 步,错误的原因是 运算顺序错误 ,第二处是第 三 步,错误的原因是 得数错误 .
(2)把正确的解题过程写出来.
【解答】解:(1)上面解题过程中有两处错误,第一处是第二步,错误的原因是运算顺序错误,第二处是第三步,错误的原因是得数错误.
(2)(﹣15)÷(13-12)×6
=(﹣15)÷(-16)×6
=(﹣15)×(﹣6)×6
=90×6
=540.
故答案为:二、运算顺序错误;三、得数错误.
21.计算:(-130)÷(23-110+16-25)
解法1:原式=(-130)÷[(23+16)+(-110-25)]=(-130)÷(56-12)=-130×3=-110
解法2:原式的倒数为:(23-110+16-25)÷(-130)=(23-110+16-25)×(﹣30)=23×(﹣30)-110×(﹣30)+16×(﹣30)-25×(﹣30)=﹣20+3﹣5+12=﹣10
故原式=-110
请阅读上述材料,选择合适的方法计算:(-142)÷(16-314+23-27)
【解答】解:原式的倒数为:(16-314+23-27)÷(-142)=(16-314+23-27)×(﹣42)=﹣7+9﹣28+12=﹣35+21=﹣14,
则原式=-114.
22.我国约有9.6×106平方千米的土地,平均1平方千米的土地一年从太阳得到的能相当于燃烧1.5×105吨煤所产生的能量
(1)一年内我国土地从太阳得到的能量相当于燃烧多少吨煤?(用科学记数法表示)
(2)若1吨煤大约可以发出8×103度电,那么(1)中的煤大约发出多少度电?(用科学记数法表示)
【解答】解:(1)(9.6×106)×(1.5×105)
=(9.6×1.5)×(106×105)
=1.44×1012(吨).
答:一年内我国土地从太阳得到的能量相当于燃烧1.44×1012吨煤.
(2)(1.44×1012)×(8×103)
=(1.44×8)×(1012×103)
=1.152×1016(度).
答:(1)中的煤大约发出1.152×1016度电.
23.某粮库6天内粮食进、出库的吨数如下(“+”表示进库,“﹣”表示出库):
+26,﹣32,﹣15,+34,﹣38,﹣20
(1)经过这6天,仓库里的粮食是增加了还是减少了?
(2)经过这6天,仓库管理员结算时发现库里还存280吨粮,那么6天前仓库里存粮多少吨?
(3)如果进出的装卸费都是每吨5元,那么这6天要付多少装卸费?
【解答】解:(1)26+(﹣32)+(﹣15)+34+(﹣38)+(﹣20)=﹣45(吨),
答:库里的粮食是减少了45吨;
(2)280+45=325(吨),
答:6天前库里有粮325吨;
(3)(26+|﹣32|+|﹣15|+34+|﹣38|+|﹣20|)×5=165×5=825(元),
答:这6天要付825元装卸费.
24.已知某粮库已存有粮食100吨,本周内粮库进出粮食的记录如下(运进为正):
星期 一 二 三 四 五 六 日
进、出记录 +35 ﹣20 ﹣30 +25 ﹣24 +50 ﹣26
(1)通过计算,说明本周内哪天粮库剩余的粮食最多?
(2)若运进的粮食为购进的,购买价格为每吨2000元,运出的粮食为卖出的,卖出的价格为每吨2300元,则这一周的利润为多少?
(3)若每周平均进出的粮食大致相同,则再过几周粮库存的粮食可达到200吨?
【解答】解:(1)星期一100+35=135吨;
星期二135﹣20=115吨;
星期三115﹣30=85吨;
星期四85+25=110吨;
星期五110﹣24=86吨;
星期六86+50=136吨;
星期日136﹣26=110吨.
故星期六最多,是136吨;
(2)2300×(20+30+24+26)﹣2000×(35+25+50)
=2300×100﹣2000×110
=230000﹣220000
=10000元;
(3)(200﹣100)÷(35+25+50﹣20﹣30﹣24﹣26)﹣1
=100÷10﹣1
=10﹣1
=9周.
故再过9周粮库存粮食达到200吨.
25.小明爸爸给小明出了一道题,说明他本月炒股的盈亏情况(单位:元)
股票 每股净赚(元) 股票
招商银行 +23 500
浙江医药 ﹣(﹣2.8) 1000
晨光文具 ﹣1.5 1500
金龙汽车 ﹣145 2000
请你也来计算一下,小明爸爸本月投资炒股到底是赔了还是赚了?赔了或赚了多少元?
【解答】解:500×23+2.8×1000﹣1.5×1500﹣1.8×2000
=4000+2800﹣2250﹣3600
=950(元)
答:赚了,赚了950元.
26.某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如下(规定向南为正,向北为负,单位:km):
第1批 第2批 第3批 第4批 第5批
5km 2km ﹣4km ﹣3km 10km
(1)接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
(3)若该出租车的计价标准为:行驶路程不超过3km收费10元,超过3km的部分按每千米加1.8元收费,在这过程中该驾驶员共收到车费多少元?
【解答】解:(1)5+2+(﹣4)+(﹣3)+10=10(km)
答:接送完第五批客人后,该驾驶员在公司的南边10千米处.
(2)(5+2+|﹣4|+|﹣3|+10)×0.2=24×0.2=4.8(升)
答:在这个过程中共耗油4.8升.
(3)[10+(5﹣3)×1.8]+10+[10+(4﹣3)×1.8]+10+[10+(10﹣3)×1.8]=68(元)
答:在这个过程中该驾驶员共收到车费68元.
27.在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.
(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;
(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.
【解答】解:(1)2+3+4=9,
9﹣6﹣4=﹣1,
9﹣6﹣2=1,
9﹣2﹣7=0,
9﹣4﹣0=5,
如图所示:
(2)﹣3+1﹣4=﹣6,
﹣6+1﹣(﹣3)=﹣2,
﹣2+1+4=3,
如图所示:
x=3﹣4﹣(﹣6)=5,
y=3﹣1﹣(﹣6)=8,
x+y=5+8=13.
28.阅读下列材料:|x|=x,x>00,x=0-x,x<0,即当x<0时,x|x|=x-x=-1.用这个结论可以解决下面问题:
(1)已知a,b是有理数,当ab≠0时,求a|a|+b|b|的值;
(2)已知a,b,c是有理数,当abc≠0时,求a|a|+b|b|+c|c|的值;
(3)已知a,b,c是有理数,a+b+c=0,abc<0,求b+c|a|+a+c|b|+a+b|c|的值.
【解答】解:(1)已知a,b是有理数,当ab≠0时,
①a<0,b<0,a|a|+b|b|=-1﹣1=﹣2;
②a>0,b>0,a|a|+b|b|=1+1=2;
③a,b异号,a|a|+b|b|=0.
故a|a|+b|b|的值为±2或0.
(2)已知a,b,c是有理数,当abc≠0时,
①a<0,b<0,c<0,a|a|+b|b|+c|c|=-1﹣1﹣1=﹣3;
②a>0,b>0,c>0,a|a|+b|b|+c|c|=1+1+1=3;
③a,b,c两负一正,a|a|+b|b|+c|c|=-1﹣1+1=﹣1;
④a,b,c两正一负,a|a|+b|b|+c|c|=-1+1+1=1.
故a|a|+b|b|+c|c|的值为±1,或±3.
(3)已知a,b,c是有理数,a+b+c=0,abc<0.
所以b+c=﹣a,a+c=﹣b,a+b=﹣c,a,b,c两正一负,
所以b+c|a|+a+c|b|+a+b|c|
=-a|a|+-b|b|+-c|c|
=﹣[a|a|+b|b|+c|c|]
=﹣1.
29.如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(结果保留π)
(1)把圆片沿数轴向左滚动1周,点A到达数轴上点C的位置,点C表示的数是 无理 数(填“无理”或“有理”),这个数是 ﹣2π ;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是 4π或﹣4π ;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3.第几次滚动后,A点距离原点最近?第几次滚动后,A点距离原点最远?
【解答】解:(1)把圆片沿数轴向左滚动1周,点A到达数轴上点C的位置,点C表示的数是无理数,这个数是﹣2π;
故答案为:无理,﹣2π;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是4π或﹣4π;
故答案为:4π或﹣4π;
(3)∵圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3,
∴第4次滚动后,A点距离原点最近;第3次滚动后,A点距离原点最远.
一.选择题(共8小题)
1.下列四个算式:①﹣2﹣3=﹣5;②2﹣|﹣3|=﹣1;③(﹣2)3=﹣6;④﹣2÷13=-6,其中正确的算式有( )
A.0个 B.1个 C.2个 D.3个
2.计算48÷(815+2435)之值为何( )
A.75 B.160 C.3158 D.902435
3.如果a、b互为相反数,c、d互为倒数,x的绝对值等于2,那么cdx2﹣a﹣b的值是( )
A.4 B.﹣4 C.4或﹣4 D.无法确定
4.在数学课上,老师让甲、乙、丙、丁,四位同学分别做了一道有理数运算题,你认为做对的同学是( )
甲:9﹣32÷8=0÷8=0
乙:24﹣(4×32)=24﹣4×6=0
丙:(36﹣12)÷32=36×23-12×23=16
丁:(﹣3)2÷13×3=9÷1=9
A.甲 B.乙 C.丙 D.丁
5.如图是一个数值运算的程序,若输出的y值为3,则输入的x值为( )
A.3.5 B.﹣3.5 C.7 D.﹣7
6.已知某快递公司的收费标准为:寄一件物品不超过5千克,收费13元;超过5千克的部分每千克加收2元.圆圆在该快递公司寄一件8千克的物品,需要付费( )
A.17元 B.19元 C.21元 D.23元
7.计算(﹣2)1999+(﹣2)2000的结果是( )
A.﹣21999 B.21999 C.﹣2 D.2
8.若“!”是一种运算符号,且1!=1,2!=2×1,3!=3×2×1,4!=4×3×2×1,…,则计算2008!2007!正确的是( )
A.2008 B.2007 C.20082007 D.2008×2007
二.填空题(共8小题)
9.(-12)3﹣1的值为 .
10.如图所示是计算机某计算程序,若开始输入x=3,则最后输出的结果是 .
11.如图,把一个长方形的礼品盒用丝带打上包装,打蝴蝶结部分需丝带45cm,那么打好整个包装所用丝带总长为 cm.
12.若a,b互为相反数,c,d互为倒数,m的绝对值为2,则a+bm+m2-cd的值是 .
13.若定义一种新运算,规定abcd=ad﹣bc,则5-3-11-2= .
14.请你只在“加、减、乘、除和括号”中选择使用,可以重复,将四个数﹣2,4,﹣6,8组成算式(四个数都用且每个数只能用一次),使运算结果为24,你列出的算式是 (只写一种)
15.如图所示的圆形工件,大圆的半径R为65.4mm,四个小圆的半径r为17.3mm,则图中阴影部分的面积是 mm2(结果保留π).
16.“转化”是一种解决问题的常用策略,有时画图可以帮助我们找到转化的方法,例如借助图(1),可以把算式1+3+5+7+9+11转化为62=36.请你观察图(2),可以把算式12+14+18+116+132转化为 = .
三.解答题(共13小题)
17.计算
(1)27﹣18+(﹣7)﹣32;
(2)(-7)÷(-34)×(-43);
(3)(-34-56+78)×(-24);
(4)-14-16×[2-(-3)2].
18.已知:a,b互为相反数,c,d互为倒数,x的绝对值是2,求x2﹣(a+b+cd)x+(a+b)2011+(﹣cd)2012的值.
19.对于有理数a、b,定义一种新运算“⊙”,规定:a⊙b=|a+b|+|a﹣b|.
(1)计算2⊙(﹣4)的值;
(2)若a,b在数轴上的位置如图所示,化简a⊙b.
20.阅读下面的解题过程:
计算(﹣15)÷(13-12)×6
解:原式=(﹣15)÷(-16)×6(第一步)
=(﹣15)÷(﹣1)(第二步)
=﹣15(第三步)
回答:(1)上面解题过程中有两处错误,第一处是第 步,错误的原因是 ,第二处是第 步,错误的原因是 .
(2)把正确的解题过程写出来.
21.计算:(-130)÷(23-110+16-25)
解法1:原式=(-130)÷[(23+16)+(-110-25)]=(-130)÷(56-12)=-130×3=-110
解法2:原式的倒数为:(23-110+16-25)÷(-130)=(23-110+16-25)×(﹣30)=23×(﹣30)-110×(﹣30)+16×(﹣30)-25×(﹣30)=﹣20+3﹣5+12=﹣10
故原式=-110
请阅读上述材料,选择合适的方法计算:(-142)÷(16-314+23-27)
22.我国约有9.6×106平方千米的土地,平均1平方千米的土地一年从太阳得到的能相当于燃烧1.5×105吨煤所产生的能量
(1)一年内我国土地从太阳得到的能量相当于燃烧多少吨煤?(用科学记数法表示)
(2)若1吨煤大约可以发出8×103度电,那么(1)中的煤大约发出多少度电?(用科学记数法表示)
23.某粮库6天内粮食进、出库的吨数如下(“+”表示进库,“﹣”表示出库):
+26,﹣32,﹣15,+34,﹣38,﹣20
(1)经过这6天,仓库里的粮食是增加了还是减少了?
(2)经过这6天,仓库管理员结算时发现库里还存280吨粮,那么6天前仓库里存粮多少吨?
(3)如果进出的装卸费都是每吨5元,那么这6天要付多少装卸费?
24.已知某粮库已存有粮食100吨,本周内粮库进出粮食的记录如下(运进为正):
星期 一 二 三 四 五 六 日
进、出记录 +35 ﹣20 ﹣30 +25 ﹣24 +50 ﹣26
(1)通过计算,说明本周内哪天粮库剩余的粮食最多?
(2)若运进的粮食为购进的,购买价格为每吨2000元,运出的粮食为卖出的,卖出的价格为每吨2300元,则这一周的利润为多少?
(3)若每周平均进出的粮食大致相同,则再过几周粮库存的粮食可达到200吨?
25.小明爸爸给小明出了一道题,说明他本月炒股的盈亏情况(单位:元)
股票 每股净赚(元) 股票
招商银行 +23 500
浙江医药 ﹣(﹣2.8) 1000
晨光文具 ﹣1.5 1500
金龙汽车 ﹣145 2000
请你也来计算一下,小明爸爸本月投资炒股到底是赔了还是赚了?赔了或赚了多少元?
26.某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如下(规定向南为正,向北为负,单位:km):
第1批 第2批 第3批 第4批 第5批
5km 2km ﹣4km ﹣3km 10km
(1)接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
(3)若该出租车的计价标准为:行驶路程不超过3km收费10元,超过3km的部分按每千米加1.8元收费,在这过程中该驾驶员共收到车费多少元?
27.在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.
(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;
(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.
28.阅读下列材料:|x|=x,x>00,x=0-x,x<0,即当x<0时,x|x|=x-x=-1.用这个结论可以解决下面问题:
(1)已知a,b是有理数,当ab≠0时,求a|a|+b|b|的值;
(2)已知a,b,c是有理数,当abc≠0时,求a|a|+b|b|+c|c|的值;
(3)已知a,b,c是有理数,a+b+c=0,abc<0,求b+c|a|+a+c|b|+a+b|c|的值.
29.如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(结果保留π)
(1)把圆片沿数轴向左滚动1周,点A到达数轴上点C的位置,点C表示的数是 数(填“无理”或“有理”),这个数是 ;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是 ;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3.第几次滚动后,A点距离原点最近?第几次滚动后,A点距离原点最远?
2.8有理数的混合运算同步练习(基础版解析)
一.选择题(共8小题)
1.下列四个算式:①﹣2﹣3=﹣5;②2﹣|﹣3|=﹣1;③(﹣2)3=﹣6;④﹣2÷13=-6,其中正确的算式有( )
A.0个 B.1个 C.2个 D.3个
【解答】解:①﹣2﹣3=﹣5,正确;
②2﹣|﹣3|=2﹣3=﹣1,正确;
③(﹣2)3=﹣8,原来的计算错误;
④﹣2÷13=-6,正确.
故其中正确的算式有3个.
故选:D.
2.计算48÷(815+2435)之值为何( )
A.75 B.160 C.3158 D.902435
【解答】解:48÷(815+2435),
=48÷(8×715×7+24×335×3),
=48÷128105,
=48×105128,
=3158.
故选:C.
3.如果a、b互为相反数,c、d互为倒数,x的绝对值等于2,那么cdx2﹣a﹣b的值是( )
A.4 B.﹣4 C.4或﹣4 D.无法确定
【解答】解:∵a、b互为相反数,c、d互为倒数,x的绝对值等于2,
∴a+b=0,cd=1,|x|=2,
∴cdx2﹣a﹣b
=1×22﹣0
=4﹣0
=4.
故选:A.
4.在数学课上,老师让甲、乙、丙、丁,四位同学分别做了一道有理数运算题,你认为做对的同学是( )
甲:9﹣32÷8=0÷8=0
乙:24﹣(4×32)=24﹣4×6=0
丙:(36﹣12)÷32=36×23-12×23=16
丁:(﹣3)2÷13×3=9÷1=9
A.甲 B.乙 C.丙 D.丁
【解答】解:甲:9﹣32÷8=9﹣9÷8=778,原来没有做对;
乙:24﹣(4×32)=24﹣4×9=﹣12,原来没有做对;
丙:(36﹣12)÷32=36×23-12×23=16,做对了;
丁:(﹣3)2÷13×3=9÷13×3=81,原来没有做对.
故选:C.
5.如图是一个数值运算的程序,若输出的y值为3,则输入的x值为( )
A.3.5 B.﹣3.5 C.7 D.﹣7
【解答】解:由题意可得,
[(﹣x)﹣1]÷2=y,
当y=3时,
[(﹣x)﹣1]÷2=3,
解得,x=﹣7,
故选:D.
6.已知某快递公司的收费标准为:寄一件物品不超过5千克,收费13元;超过5千克的部分每千克加收2元.圆圆在该快递公司寄一件8千克的物品,需要付费( )
A.17元 B.19元 C.21元 D.23元
【解答】解:根据题意得:13+(8﹣5)×2=13+6=19(元).
则需要付费19元.
故选:B.
7.计算(﹣2)1999+(﹣2)2000的结果是( )
A.﹣21999 B.21999 C.﹣2 D.2
【解答】解:(﹣2)1999+(﹣2)2000
=2×21999﹣21999
=21999(2﹣1)
=21999.
故选:B.
8.若“!”是一种运算符号,且1!=1,2!=2×1,3!=3×2×1,4!=4×3×2×1,…,则计算2008!2007!正确的是( )
A.2008 B.2007 C.20082007 D.2008×2007
【解答】解:2008!2007!=2008×2007×2006× ×12007×2006× ×1=2008.
故选:A.
二.填空题(共8小题)
9.(-12)3﹣1的值为 -118 .
【解答】解:(-12)3﹣1
=-18-1
=﹣118.
故答案为:﹣118.
10.如图所示是计算机某计算程序,若开始输入x=3,则最后输出的结果是 38 .
【解答】解:根据题意可知,3×4﹣2=10=10,
所以再把10代入计算:10×4﹣2=38>10,
即38为最后结果.
故本题答案为:38.
11.如图,把一个长方形的礼品盒用丝带打上包装,打蝴蝶结部分需丝带45cm,那么打好整个包装所用丝带总长为 143 cm.
【解答】解:2×10+2×15+4×12+45=143cm.故填143.
12.若a,b互为相反数,c,d互为倒数,m的绝对值为2,则a+bm+m2-cd的值是 3 .
【解答】解:∵a,b互为相反数,c,d互为倒数,m的绝对值为2,
∴a+b=0,cd=1,|m|=2,
∴m2=4,
若m=2,则a+bm+m2-cd=02+4﹣1=3,
若m=﹣2,则a+bm+m2-cd=0-2+4﹣1=3,
∴a+bm+m2-cd=3.
故答案为:3.
13.若定义一种新运算,规定abcd=ad﹣bc,则5-3-11-2= ﹣43 .
【解答】解:∵abcd=ad﹣bc,
∴5-3-11-2
=5×(﹣2)﹣(﹣3)×(﹣11)
=﹣10﹣33
=﹣43.
故答案为:﹣43.
14.请你只在“加、减、乘、除和括号”中选择使用,可以重复,将四个数﹣2,4,﹣6,8组成算式(四个数都用且每个数只能用一次),使运算结果为24,你列出的算式是 8×(﹣6)÷[4÷(﹣2)]=24 (只写一种)
【解答】解:8×(﹣6)÷[4÷(﹣2)]=24
故答案为:8×(﹣6)÷[4÷(﹣2)]=24.(答案不唯一)
15.如图所示的圆形工件,大圆的半径R为65.4mm,四个小圆的半径r为17.3mm,则图中阴影部分的面积是 3080π mm2(结果保留π).
【解答】解:S阴影=S大圆﹣4S小圆
=πR2﹣4πr2=π(R2﹣4r2)
=π(R+2r)(R﹣2r)
=π(65.4+34.6)(65.4﹣34.6)
=3080π.
故答案为3080πmm2.
16.“转化”是一种解决问题的常用策略,有时画图可以帮助我们找到转化的方法,例如借助图(1),可以把算式1+3+5+7+9+11转化为62=36.请你观察图(2),可以把算式12+14+18+116+132转化为 1-132 = 3132 .
【解答】解:观察图(2),可以把算式12+14+18+116+132转化为 1-132=3132.
故答案为:1-132,3132.
三.解答题(共13小题)
17.计算
(1)27﹣18+(﹣7)﹣32;
(2)(-7)÷(-34)×(-43);
(3)(-34-56+78)×(-24);
(4)-14-16×[2-(-3)2].
【解答】解:(1)27﹣18+(﹣7)﹣32
=27﹣18﹣7﹣32
=27﹣57
=﹣30;
(2)(-7)÷(-34)×(-43)
=﹣7×43×43
=-1129;
(3)(-34-56+78)×(-24)
=-34×(﹣24)-56×(﹣24)+78×(﹣24)
=18+20﹣21
=17;
(4)-14-16×[2-(-3)2]
=﹣1-16×(2﹣9)
=﹣1-16×(﹣7)
=﹣1+76
=16.
18.已知:a,b互为相反数,c,d互为倒数,x的绝对值是2,求x2﹣(a+b+cd)x+(a+b)2011+(﹣cd)2012的值.
【解答】解:由已知可得,a+b=0,cd=1,x=±2;
当x=2时,
x2﹣(a+b+cd)x+(a+b)2011+(﹣cd)2012
=22﹣(0+1)×2+02011+(﹣1)2012
=4﹣2+0+1
=3
当x=﹣2时,
x2﹣(a+b+cd)x+(a+b)2011+(﹣cd)2012
=(﹣2)2﹣(0+1)×(﹣2)+02011+(﹣1)2012
=4+2+0+1
=7
19.对于有理数a、b,定义一种新运算“⊙”,规定:a⊙b=|a+b|+|a﹣b|.
(1)计算2⊙(﹣4)的值;
(2)若a,b在数轴上的位置如图所示,化简a⊙b.
【解答】解:(1)2⊙(﹣4)=|2﹣4|+|2+4|=2+6=8;
(2)由数轴知a<0<b,且|a|>|b|,
则a+b<0、a﹣b<0,
所以原式=﹣(a+b)﹣(a﹣b)
=﹣a﹣b﹣a+b
=﹣2a.
20.阅读下面的解题过程:
计算(﹣15)÷(13-12)×6
解:原式=(﹣15)÷(-16)×6(第一步)
=(﹣15)÷(﹣1)(第二步)
=﹣15(第三步)
回答:(1)上面解题过程中有两处错误,第一处是第 二 步,错误的原因是 运算顺序错误 ,第二处是第 三 步,错误的原因是 得数错误 .
(2)把正确的解题过程写出来.
【解答】解:(1)上面解题过程中有两处错误,第一处是第二步,错误的原因是运算顺序错误,第二处是第三步,错误的原因是得数错误.
(2)(﹣15)÷(13-12)×6
=(﹣15)÷(-16)×6
=(﹣15)×(﹣6)×6
=90×6
=540.
故答案为:二、运算顺序错误;三、得数错误.
21.计算:(-130)÷(23-110+16-25)
解法1:原式=(-130)÷[(23+16)+(-110-25)]=(-130)÷(56-12)=-130×3=-110
解法2:原式的倒数为:(23-110+16-25)÷(-130)=(23-110+16-25)×(﹣30)=23×(﹣30)-110×(﹣30)+16×(﹣30)-25×(﹣30)=﹣20+3﹣5+12=﹣10
故原式=-110
请阅读上述材料,选择合适的方法计算:(-142)÷(16-314+23-27)
【解答】解:原式的倒数为:(16-314+23-27)÷(-142)=(16-314+23-27)×(﹣42)=﹣7+9﹣28+12=﹣35+21=﹣14,
则原式=-114.
22.我国约有9.6×106平方千米的土地,平均1平方千米的土地一年从太阳得到的能相当于燃烧1.5×105吨煤所产生的能量
(1)一年内我国土地从太阳得到的能量相当于燃烧多少吨煤?(用科学记数法表示)
(2)若1吨煤大约可以发出8×103度电,那么(1)中的煤大约发出多少度电?(用科学记数法表示)
【解答】解:(1)(9.6×106)×(1.5×105)
=(9.6×1.5)×(106×105)
=1.44×1012(吨).
答:一年内我国土地从太阳得到的能量相当于燃烧1.44×1012吨煤.
(2)(1.44×1012)×(8×103)
=(1.44×8)×(1012×103)
=1.152×1016(度).
答:(1)中的煤大约发出1.152×1016度电.
23.某粮库6天内粮食进、出库的吨数如下(“+”表示进库,“﹣”表示出库):
+26,﹣32,﹣15,+34,﹣38,﹣20
(1)经过这6天,仓库里的粮食是增加了还是减少了?
(2)经过这6天,仓库管理员结算时发现库里还存280吨粮,那么6天前仓库里存粮多少吨?
(3)如果进出的装卸费都是每吨5元,那么这6天要付多少装卸费?
【解答】解:(1)26+(﹣32)+(﹣15)+34+(﹣38)+(﹣20)=﹣45(吨),
答:库里的粮食是减少了45吨;
(2)280+45=325(吨),
答:6天前库里有粮325吨;
(3)(26+|﹣32|+|﹣15|+34+|﹣38|+|﹣20|)×5=165×5=825(元),
答:这6天要付825元装卸费.
24.已知某粮库已存有粮食100吨,本周内粮库进出粮食的记录如下(运进为正):
星期 一 二 三 四 五 六 日
进、出记录 +35 ﹣20 ﹣30 +25 ﹣24 +50 ﹣26
(1)通过计算,说明本周内哪天粮库剩余的粮食最多?
(2)若运进的粮食为购进的,购买价格为每吨2000元,运出的粮食为卖出的,卖出的价格为每吨2300元,则这一周的利润为多少?
(3)若每周平均进出的粮食大致相同,则再过几周粮库存的粮食可达到200吨?
【解答】解:(1)星期一100+35=135吨;
星期二135﹣20=115吨;
星期三115﹣30=85吨;
星期四85+25=110吨;
星期五110﹣24=86吨;
星期六86+50=136吨;
星期日136﹣26=110吨.
故星期六最多,是136吨;
(2)2300×(20+30+24+26)﹣2000×(35+25+50)
=2300×100﹣2000×110
=230000﹣220000
=10000元;
(3)(200﹣100)÷(35+25+50﹣20﹣30﹣24﹣26)﹣1
=100÷10﹣1
=10﹣1
=9周.
故再过9周粮库存粮食达到200吨.
25.小明爸爸给小明出了一道题,说明他本月炒股的盈亏情况(单位:元)
股票 每股净赚(元) 股票
招商银行 +23 500
浙江医药 ﹣(﹣2.8) 1000
晨光文具 ﹣1.5 1500
金龙汽车 ﹣145 2000
请你也来计算一下,小明爸爸本月投资炒股到底是赔了还是赚了?赔了或赚了多少元?
【解答】解:500×23+2.8×1000﹣1.5×1500﹣1.8×2000
=4000+2800﹣2250﹣3600
=950(元)
答:赚了,赚了950元.
26.某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如下(规定向南为正,向北为负,单位:km):
第1批 第2批 第3批 第4批 第5批
5km 2km ﹣4km ﹣3km 10km
(1)接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
(3)若该出租车的计价标准为:行驶路程不超过3km收费10元,超过3km的部分按每千米加1.8元收费,在这过程中该驾驶员共收到车费多少元?
【解答】解:(1)5+2+(﹣4)+(﹣3)+10=10(km)
答:接送完第五批客人后,该驾驶员在公司的南边10千米处.
(2)(5+2+|﹣4|+|﹣3|+10)×0.2=24×0.2=4.8(升)
答:在这个过程中共耗油4.8升.
(3)[10+(5﹣3)×1.8]+10+[10+(4﹣3)×1.8]+10+[10+(10﹣3)×1.8]=68(元)
答:在这个过程中该驾驶员共收到车费68元.
27.在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.
(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;
(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.
【解答】解:(1)2+3+4=9,
9﹣6﹣4=﹣1,
9﹣6﹣2=1,
9﹣2﹣7=0,
9﹣4﹣0=5,
如图所示:
(2)﹣3+1﹣4=﹣6,
﹣6+1﹣(﹣3)=﹣2,
﹣2+1+4=3,
如图所示:
x=3﹣4﹣(﹣6)=5,
y=3﹣1﹣(﹣6)=8,
x+y=5+8=13.
28.阅读下列材料:|x|=x,x>00,x=0-x,x<0,即当x<0时,x|x|=x-x=-1.用这个结论可以解决下面问题:
(1)已知a,b是有理数,当ab≠0时,求a|a|+b|b|的值;
(2)已知a,b,c是有理数,当abc≠0时,求a|a|+b|b|+c|c|的值;
(3)已知a,b,c是有理数,a+b+c=0,abc<0,求b+c|a|+a+c|b|+a+b|c|的值.
【解答】解:(1)已知a,b是有理数,当ab≠0时,
①a<0,b<0,a|a|+b|b|=-1﹣1=﹣2;
②a>0,b>0,a|a|+b|b|=1+1=2;
③a,b异号,a|a|+b|b|=0.
故a|a|+b|b|的值为±2或0.
(2)已知a,b,c是有理数,当abc≠0时,
①a<0,b<0,c<0,a|a|+b|b|+c|c|=-1﹣1﹣1=﹣3;
②a>0,b>0,c>0,a|a|+b|b|+c|c|=1+1+1=3;
③a,b,c两负一正,a|a|+b|b|+c|c|=-1﹣1+1=﹣1;
④a,b,c两正一负,a|a|+b|b|+c|c|=-1+1+1=1.
故a|a|+b|b|+c|c|的值为±1,或±3.
(3)已知a,b,c是有理数,a+b+c=0,abc<0.
所以b+c=﹣a,a+c=﹣b,a+b=﹣c,a,b,c两正一负,
所以b+c|a|+a+c|b|+a+b|c|
=-a|a|+-b|b|+-c|c|
=﹣[a|a|+b|b|+c|c|]
=﹣1.
29.如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(结果保留π)
(1)把圆片沿数轴向左滚动1周,点A到达数轴上点C的位置,点C表示的数是 无理 数(填“无理”或“有理”),这个数是 ﹣2π ;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是 4π或﹣4π ;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3.第几次滚动后,A点距离原点最近?第几次滚动后,A点距离原点最远?
【解答】解:(1)把圆片沿数轴向左滚动1周,点A到达数轴上点C的位置,点C表示的数是无理数,这个数是﹣2π;
故答案为:无理,﹣2π;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是4π或﹣4π;
故答案为:4π或﹣4π;
(3)∵圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3,
∴第4次滚动后,A点距离原点最近;第3次滚动后,A点距离原点最远.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
