一元一次不等式和一元一次不等式组全章测试(一)
文档属性
| 名称 | 一元一次不等式和一元一次不等式组全章测试(一) |
|
|
| 格式 | rar | ||
| 文件大小 | 56.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-14 00:00:00 | ||
图片预览
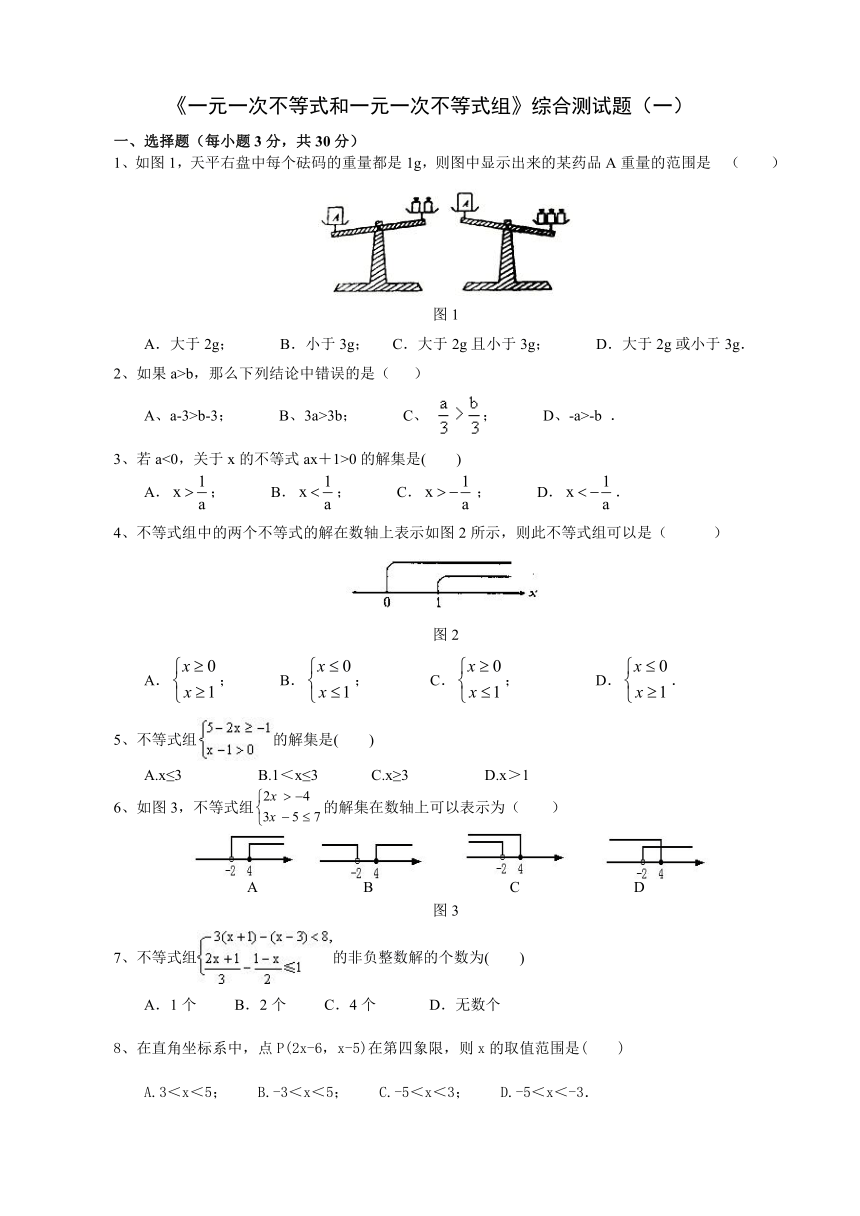


文档简介
《一元一次不等式和一元一次不等式组》综合测试题(一)
一、选择题(每小题3分,共30分)
1、如图1,天平右盘中每个砝码的重量都是1g,则图中显示出来的某药品A重量的范围是 ( )
图1
A.大于2g; B.小于3g; C.大于2g且小于3g; D.大于2g或小于3g.
2、如果a>b,那么下列结论中错误的是( )
A、a-3>b-3; B、3a>3b; C、 ; D、-a>-b .
3、若a<0,关于x的不等式ax+1>0的解集是( )
A.; B.; C. ; D..
4、不等式组中的两个不等式的解在数轴上表示如图2所示,则此不等式组可以是( )
图2
A.; B.; C.; D..
5、不等式组的解集是( )
A.x≤3 B.1<x≤3 C.x≥3 D.x>1
6、如图3,不等式组的解集在数轴上可以表示为( )
A B C D
图3
7、不等式组的非负整数解的个数为( )
A.1个 B.2个 C.4个 D.无数个
8、在直角坐标系中,点P(2x-6,x-5)在第四象限,则x的取值范围是( )
A.3<x<5; B.-3<x<5; C.-5<x<3; D.-5<x<-3.
9、已知关于x的不等式组无解,则a的取值范围是( )
A.a ≤-1 B.a≥2 C. -1<a<2 D. a<-1,或a>2
10、在一次“人与自然”知识竞赛中,竞赛试题共有25道题,每道题都给出了4个答案,其中只有一个答案是对的,要求学生把正确答案选出来,每道题选对得4分,不选或错选扣2分,如果小刚在本次竞赛中,得分不低于60分,那么他至少选对( )
A.18道 B.19道 C.20道 D.21道
二、填空题(每小题3分,共30分)
11、写出不等式的一个整数解:_______.
12、图4表示的不等式组的解集为________.
图4
13、不等式组的解集是________.
14、现有长度分别为2、3的两根木棒,再取一根木棒,钉成一个三角形,则第三根木棒的长度a的取值范围为_______.
15、不等式组的整数解是________.
16、不等式组 的整数解之和为________.
17、在平面直角坐标系内,已知点(1-2a,a-2)在第三象限,且a为整数,则a的值为________.
18、已知关于x的不等式组 的整数解共5个,则a的取值范围是________.
19、小华家距离学校2.4千米.某一天小华从家中去上学恰好行走到一半的路程时,发现离到校时间只有12分钟了.如果小华能按时赶到学校,那么他行走剩下的一半路程的平均速度至少要达到__________千米/分.
20、乘某城市的一种出租汽车起价是10元(即行驶路程在5km以内都需付10元车费),达到或超过5km后,每增加1km加价1.2元(不足1km部分按1km计).现在某人乘这种出租汽车从甲地到乙地,支付车费17.2元,从甲地到乙地的路大约是为xkm,则x的取值范围是____________.
三、解答题(每小题7分,共35分)
21、解不等式.
22、已知:2x-3≤5(x-3)和,则比较x、y的大小.
23、解不等式组,把解集在数轴上表示,并求它的非负整数解.
24、商场出售的A型冰箱每台售价2190元,每日耗电量为1度,而B型节能冰箱每台售价虽比A型冰箱高出10%,但每日耗电量却为0.55度.现将A型冰箱打折出售(打一折后的售价为原价的 ),问商场至少打几折,消费者购买才合算(按使用期为10年,每年365天,每度电0.40元计算)?
25、某夏令营的活动时间为15天,营员的宿舍安装了空调.如果某间宿舍每天比原计划多开2个小时的空调,那么开空调的总时间超过150小时;如果每天比原计划少开2个小时的空调,那么开空调的总时间不足120小时,问原计划每天开空调时间为多少小时?
四、探索题(第26、27小题,每小题8分,第28小题9分,共25分)
26、比较下面两列算式结果的大小(在横线上选“>”“<”“=”)
(1),
,
,
…
通过观察归纳,得。
(2)写出能反映这种规律的一般结论:_________.
(3)用所学知识说明所得结论的正确性.
27、m为何整数时,关于x、y的方程组 的解是非负数?
28、某水果批发市场香蕉的价格如下表:
购买香蕉数(千克) 不超过20千克 20千克以上但不超过40千克 40千克以上
每千克价格 6元 5元 4元
张强两次共购买香蕉50千克(第二次多于第一次),共付款264元.由此,你能知道张强第一次、第二次分别购买香蕉多少千克吗 如果能,请求出结果;如果不能,请添加一个合理的条件,然后求出结果.
参考答案
一、C D D A B,D A A B B.
二、11、提示:小于5的整数都可以; 12、-4≤<-1; 13、<x<4; 14、115、-1,0; 16、3; 17、1; 18、- 4三、21、小数化为分数,得
去分母,得
4(2x-1)-6(3x-5)-2(x+1)+3×5>0
去括号,得
8x-4-18x+30-2x-2+15>0
合并,得
-12x+39>0
移项,得
-12x>-39
系数化为1,得
22、分别求出两个不等式的解集.
由2x-3≤5(x-3),得
x≥4
由,得
y<-9
故x>y.
23、由不等式2x+1<3x+3,得
x>-2
由不等式,得
x≤5
所以原不等式组的解集是
-2将所得不等式组的解集在数轴上表示如下图:
可见,它的非负整数解为0,1,2,3,4,5这六个数.
24、设商场将A型冰箱打x折出售,消费者购买才合算,依题意,有
2190× +365×10×1×0.4≤2190×(1+10%)+365×10×0.55×0.4
即
219x+1460≤2409+803
解这个不等式,得
x≤8
答:商场应将A型冰箱至少打八折出售,消费者购买才合算.
25、设原计划某间宿舍每天开空调时间为x小时,依题意,得
解得
8<x<10
答:原计划某间宿舍每天开空调时间为8至10小时.
四、26、(1)>,>,=,>;
(2);
(2)由,得.
27、解方程组 ,得
因为方程组 的解是非负数,所以 ,
即
解不等式组
所以,此不等式组解集为
≤m≤
又因为m为整数,
所以,m=3或m=4.
28、根据现有条件,能求出张强第一次、第二次分别购买香蕉多少千克.
设张强第一次购买香蕉x千克,第二次购买香蕉y千克.由题意,得0①当0②当040时,由题意,得
(不合题意,舍去).
③当20此时张强用去的款项为5x+5y=5(x+y)=5×50=250<264(不合题意,舍去).
综合①②③可知,张强第一次购买香蕉14千克,第二次购买香蕉36千克.
2(x+2)≤3x+3
一、选择题(每小题3分,共30分)
1、如图1,天平右盘中每个砝码的重量都是1g,则图中显示出来的某药品A重量的范围是 ( )
图1
A.大于2g; B.小于3g; C.大于2g且小于3g; D.大于2g或小于3g.
2、如果a>b,那么下列结论中错误的是( )
A、a-3>b-3; B、3a>3b; C、 ; D、-a>-b .
3、若a<0,关于x的不等式ax+1>0的解集是( )
A.; B.; C. ; D..
4、不等式组中的两个不等式的解在数轴上表示如图2所示,则此不等式组可以是( )
图2
A.; B.; C.; D..
5、不等式组的解集是( )
A.x≤3 B.1<x≤3 C.x≥3 D.x>1
6、如图3,不等式组的解集在数轴上可以表示为( )
A B C D
图3
7、不等式组的非负整数解的个数为( )
A.1个 B.2个 C.4个 D.无数个
8、在直角坐标系中,点P(2x-6,x-5)在第四象限,则x的取值范围是( )
A.3<x<5; B.-3<x<5; C.-5<x<3; D.-5<x<-3.
9、已知关于x的不等式组无解,则a的取值范围是( )
A.a ≤-1 B.a≥2 C. -1<a<2 D. a<-1,或a>2
10、在一次“人与自然”知识竞赛中,竞赛试题共有25道题,每道题都给出了4个答案,其中只有一个答案是对的,要求学生把正确答案选出来,每道题选对得4分,不选或错选扣2分,如果小刚在本次竞赛中,得分不低于60分,那么他至少选对( )
A.18道 B.19道 C.20道 D.21道
二、填空题(每小题3分,共30分)
11、写出不等式的一个整数解:_______.
12、图4表示的不等式组的解集为________.
图4
13、不等式组的解集是________.
14、现有长度分别为2、3的两根木棒,再取一根木棒,钉成一个三角形,则第三根木棒的长度a的取值范围为_______.
15、不等式组的整数解是________.
16、不等式组 的整数解之和为________.
17、在平面直角坐标系内,已知点(1-2a,a-2)在第三象限,且a为整数,则a的值为________.
18、已知关于x的不等式组 的整数解共5个,则a的取值范围是________.
19、小华家距离学校2.4千米.某一天小华从家中去上学恰好行走到一半的路程时,发现离到校时间只有12分钟了.如果小华能按时赶到学校,那么他行走剩下的一半路程的平均速度至少要达到__________千米/分.
20、乘某城市的一种出租汽车起价是10元(即行驶路程在5km以内都需付10元车费),达到或超过5km后,每增加1km加价1.2元(不足1km部分按1km计).现在某人乘这种出租汽车从甲地到乙地,支付车费17.2元,从甲地到乙地的路大约是为xkm,则x的取值范围是____________.
三、解答题(每小题7分,共35分)
21、解不等式.
22、已知:2x-3≤5(x-3)和,则比较x、y的大小.
23、解不等式组,把解集在数轴上表示,并求它的非负整数解.
24、商场出售的A型冰箱每台售价2190元,每日耗电量为1度,而B型节能冰箱每台售价虽比A型冰箱高出10%,但每日耗电量却为0.55度.现将A型冰箱打折出售(打一折后的售价为原价的 ),问商场至少打几折,消费者购买才合算(按使用期为10年,每年365天,每度电0.40元计算)?
25、某夏令营的活动时间为15天,营员的宿舍安装了空调.如果某间宿舍每天比原计划多开2个小时的空调,那么开空调的总时间超过150小时;如果每天比原计划少开2个小时的空调,那么开空调的总时间不足120小时,问原计划每天开空调时间为多少小时?
四、探索题(第26、27小题,每小题8分,第28小题9分,共25分)
26、比较下面两列算式结果的大小(在横线上选“>”“<”“=”)
(1),
,
,
…
通过观察归纳,得。
(2)写出能反映这种规律的一般结论:_________.
(3)用所学知识说明所得结论的正确性.
27、m为何整数时,关于x、y的方程组 的解是非负数?
28、某水果批发市场香蕉的价格如下表:
购买香蕉数(千克) 不超过20千克 20千克以上但不超过40千克 40千克以上
每千克价格 6元 5元 4元
张强两次共购买香蕉50千克(第二次多于第一次),共付款264元.由此,你能知道张强第一次、第二次分别购买香蕉多少千克吗 如果能,请求出结果;如果不能,请添加一个合理的条件,然后求出结果.
参考答案
一、C D D A B,D A A B B.
二、11、提示:小于5的整数都可以; 12、-4≤<-1; 13、<x<4; 14、1
去分母,得
4(2x-1)-6(3x-5)-2(x+1)+3×5>0
去括号,得
8x-4-18x+30-2x-2+15>0
合并,得
-12x+39>0
移项,得
-12x>-39
系数化为1,得
22、分别求出两个不等式的解集.
由2x-3≤5(x-3),得
x≥4
由,得
y<-9
故x>y.
23、由不等式2x+1<3x+3,得
x>-2
由不等式,得
x≤5
所以原不等式组的解集是
-2
可见,它的非负整数解为0,1,2,3,4,5这六个数.
24、设商场将A型冰箱打x折出售,消费者购买才合算,依题意,有
2190× +365×10×1×0.4≤2190×(1+10%)+365×10×0.55×0.4
即
219x+1460≤2409+803
解这个不等式,得
x≤8
答:商场应将A型冰箱至少打八折出售,消费者购买才合算.
25、设原计划某间宿舍每天开空调时间为x小时,依题意,得
解得
8<x<10
答:原计划某间宿舍每天开空调时间为8至10小时.
四、26、(1)>,>,=,>;
(2);
(2)由,得.
27、解方程组 ,得
因为方程组 的解是非负数,所以 ,
即
解不等式组
所以,此不等式组解集为
≤m≤
又因为m为整数,
所以,m=3或m=4.
28、根据现有条件,能求出张强第一次、第二次分别购买香蕉多少千克.
设张强第一次购买香蕉x千克,第二次购买香蕉y千克.由题意,得0
(不合题意,舍去).
③当20
综合①②③可知,张强第一次购买香蕉14千克,第二次购买香蕉36千克.
2(x+2)≤3x+3
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
