2023-2024学年人教版七年级数学上册4.1.1立体图形与平面图形同步练习(含简单答案)
文档属性
| 名称 | 2023-2024学年人教版七年级数学上册4.1.1立体图形与平面图形同步练习(含简单答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 645.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-15 18:12:12 | ||
图片预览


文档简介
4.1.1立体图形与平面图形 同步练习
一、单选题
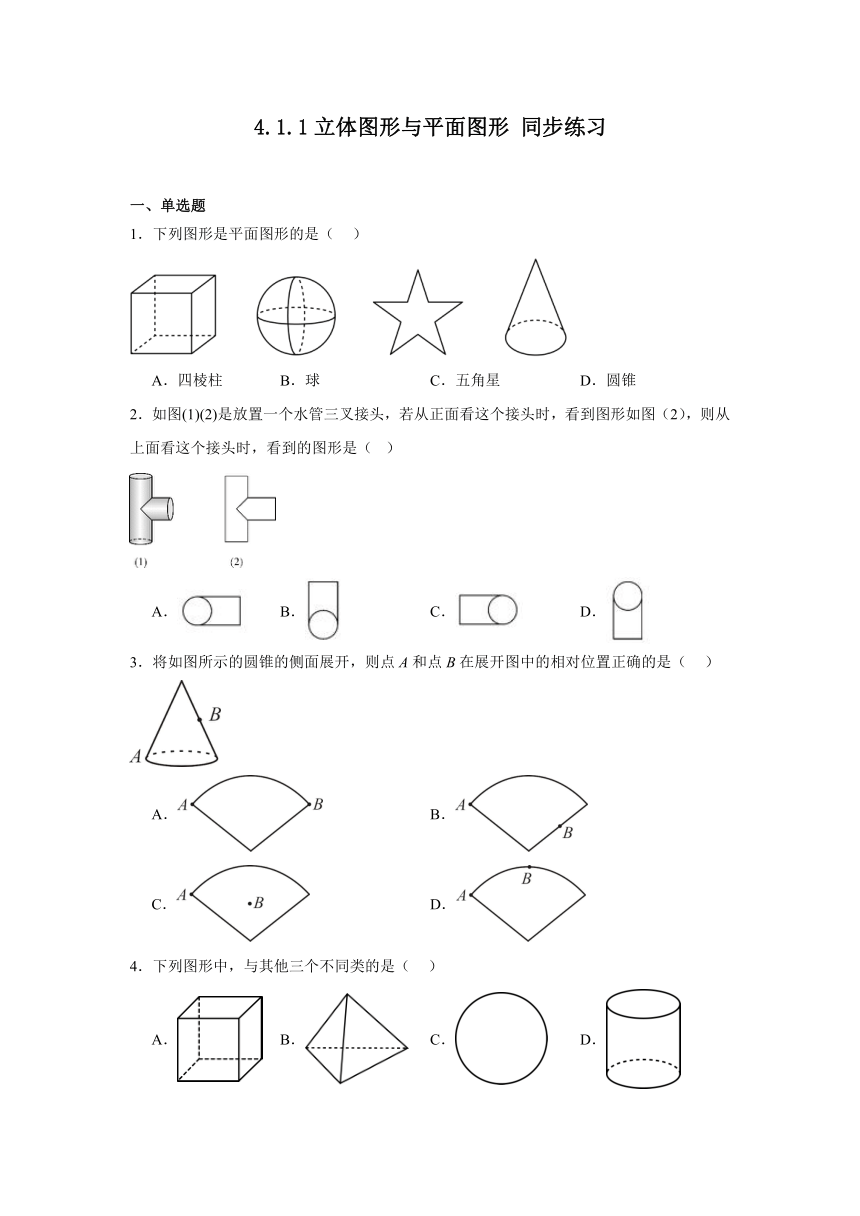
1.下列图形是平面图形的是( )
A.四棱柱 B.球 C.五角星 D.圆锥
2.如图(1)(2)是放置一个水管三叉接头,若从正面看这个接头时,看到图形如图(2),则从上面看这个接头时,看到的图形是( )
A. B. C. D.
3.将如图所示的圆锥的侧面展开,则点A和点B在展开图中的相对位置正确的是( )
A. B.
C. D.
4.下列图形中,与其他三个不同类的是( )
A. B. C. D.
5.将如图折成一个正方体,点与( )会重合.
A.点 B.点 C.点 D.点
6.如图所示为几何体的平面展开图,则从左到右,其对应的几何体名称分别为( )
A.圆锥,正方体,三棱锥,圆柱 B.正方体,圆锥,四棱锥,圆柱
C.正方体,圆锥,四棱柱,圆柱 D.正方体,圆锥,圆柱,三棱柱
7.小林同学在一个正方体盒子的每个面上都写有一个字,分别是:我、喜、欢、数、学、课,其平面展开图如图所示,那么在该正方体盒子中,和“我”相对的面所写的字是( )
A.欢 B.学 C.数 D.课
8.如图,若已知七巧板拼图中的平行四边形的面积为则图中,最大正方形面积为( )
A. B. C. D.
二、填空题
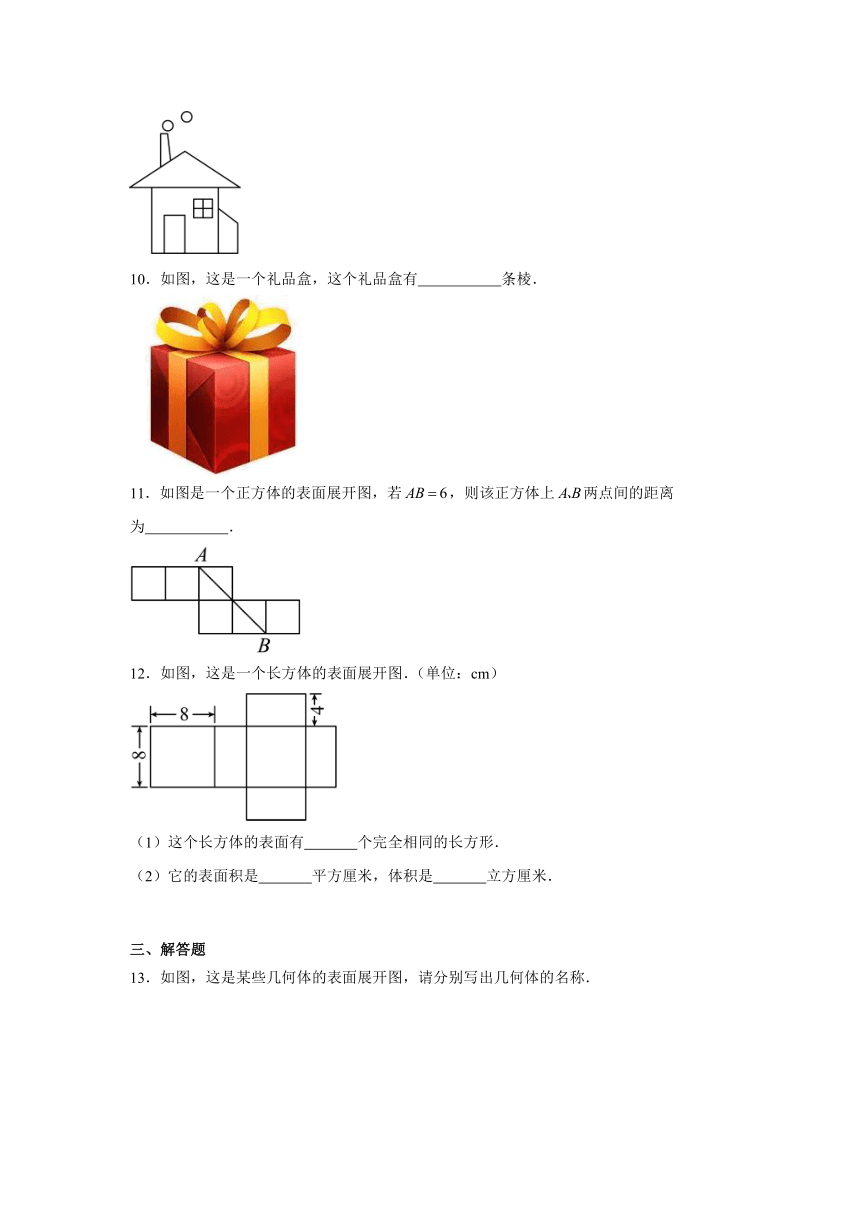
9.如图所示是一座房子的图片,其中的图形有 .
10.如图,这是一个礼品盒,这个礼品盒有 条棱.
11.如图是一个正方体的表面展开图,若,则该正方体上两点间的距离为 .
12.如图,这是一个长方体的表面展开图.(单位:cm)
(1)这个长方体的表面有 个完全相同的长方形.
(2)它的表面积是 平方厘米,体积是 立方厘米.
三、解答题
13.如图,这是某些几何体的表面展开图,请分别写出几何体的名称.
14.如图是由个相同的小正方体搭成的几何体,画出该几何体的主视图、左视图和俯视图.
15.如图,请写出下列立体图形是由哪些几何体组合而成的.
16.如图,某同学在制作正方体模型时,在方格纸上画出几个小正方形图中阴影部分,但由于疏忽少画了一个,请你用两种不同的方法,在下面两个方格纸上分别用阴影补上,使之可以折叠成正方体.
17.如图所示,圆柱的高4cm,底面半径3cm,请求出该圆柱的表面积和体积.
18.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型得
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4 4 6
长方体 8 6 12
正八面体 6 8 12
正十二面体 20 12 30
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系是__________________.
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是__________.
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表三角形的个数为x个,八边形的个数为y个,求x+y的值.
参考答案
1.C
2.A
3.C
4.C
5.D
6.D
7.B
8.C
9.三角形、四边形、长方形、正方形、梯形、圆
10.12
11.3
12.4 256 256
13.图1为五棱锥,图2为五棱柱
14.
15.解:图1是由底面完全重合的圆维和圆柱组合而成的;图2是由底面完全重合的两个圆锥组合而成的;图3是由完全相同的四个正方体组合而成的
16.
17.圆柱体积:36πcm3;圆柱表面积:42πcm2
18.(1);(2);(3)
一、单选题
1.下列图形是平面图形的是( )
A.四棱柱 B.球 C.五角星 D.圆锥
2.如图(1)(2)是放置一个水管三叉接头,若从正面看这个接头时,看到图形如图(2),则从上面看这个接头时,看到的图形是( )
A. B. C. D.
3.将如图所示的圆锥的侧面展开,则点A和点B在展开图中的相对位置正确的是( )
A. B.
C. D.
4.下列图形中,与其他三个不同类的是( )
A. B. C. D.
5.将如图折成一个正方体,点与( )会重合.
A.点 B.点 C.点 D.点
6.如图所示为几何体的平面展开图,则从左到右,其对应的几何体名称分别为( )
A.圆锥,正方体,三棱锥,圆柱 B.正方体,圆锥,四棱锥,圆柱
C.正方体,圆锥,四棱柱,圆柱 D.正方体,圆锥,圆柱,三棱柱
7.小林同学在一个正方体盒子的每个面上都写有一个字,分别是:我、喜、欢、数、学、课,其平面展开图如图所示,那么在该正方体盒子中,和“我”相对的面所写的字是( )
A.欢 B.学 C.数 D.课
8.如图,若已知七巧板拼图中的平行四边形的面积为则图中,最大正方形面积为( )
A. B. C. D.
二、填空题
9.如图所示是一座房子的图片,其中的图形有 .
10.如图,这是一个礼品盒,这个礼品盒有 条棱.
11.如图是一个正方体的表面展开图,若,则该正方体上两点间的距离为 .
12.如图,这是一个长方体的表面展开图.(单位:cm)
(1)这个长方体的表面有 个完全相同的长方形.
(2)它的表面积是 平方厘米,体积是 立方厘米.
三、解答题
13.如图,这是某些几何体的表面展开图,请分别写出几何体的名称.
14.如图是由个相同的小正方体搭成的几何体,画出该几何体的主视图、左视图和俯视图.
15.如图,请写出下列立体图形是由哪些几何体组合而成的.
16.如图,某同学在制作正方体模型时,在方格纸上画出几个小正方形图中阴影部分,但由于疏忽少画了一个,请你用两种不同的方法,在下面两个方格纸上分别用阴影补上,使之可以折叠成正方体.
17.如图所示,圆柱的高4cm,底面半径3cm,请求出该圆柱的表面积和体积.
18.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型得
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4 4 6
长方体 8 6 12
正八面体 6 8 12
正十二面体 20 12 30
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系是__________________.
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是__________.
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表三角形的个数为x个,八边形的个数为y个,求x+y的值.
参考答案
1.C
2.A
3.C
4.C
5.D
6.D
7.B
8.C
9.三角形、四边形、长方形、正方形、梯形、圆
10.12
11.3
12.4 256 256
13.图1为五棱锥,图2为五棱柱
14.
15.解:图1是由底面完全重合的圆维和圆柱组合而成的;图2是由底面完全重合的两个圆锥组合而成的;图3是由完全相同的四个正方体组合而成的
16.
17.圆柱体积:36πcm3;圆柱表面积:42πcm2
18.(1);(2);(3)
