2023学年鲁教版数学五四制八年级上册同步教学 5.2.2平行四边形的判定 课件(共15张PPT)
文档属性
| 名称 | 2023学年鲁教版数学五四制八年级上册同步教学 5.2.2平行四边形的判定 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 468.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-15 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
5.2.2平行四边形的判定
教学目标
知识技能目标
1.运用类比的方法,通过学生的合作探究,得出平行四边形的判定方法.
2.理解一组对边平行且相等的四边形是平行四边形这一判定定理,并学会简单运用.
过程与方法目标
1.经历平行四边行判别条件的探索过程,在探究活动中发展学生的合情推理意识.
2.在运用平行四边形的判定方法解决问题的过程中,进一步培养和发展学生的逻辑思维能力和推理论证的几何表达能力.
教学重点:平行四边形判定方法的综合运用.
教学难点:平行四边形的性质和判定的综合运用.
定理1:两组对边分别相等的四边形是平行四边形
说一说:我们已经学过平行四边形的哪些判定方法
定义: 两组对边分别平行的四边形是平行四边形
两组对角分别相等的四边形是平行四边形.
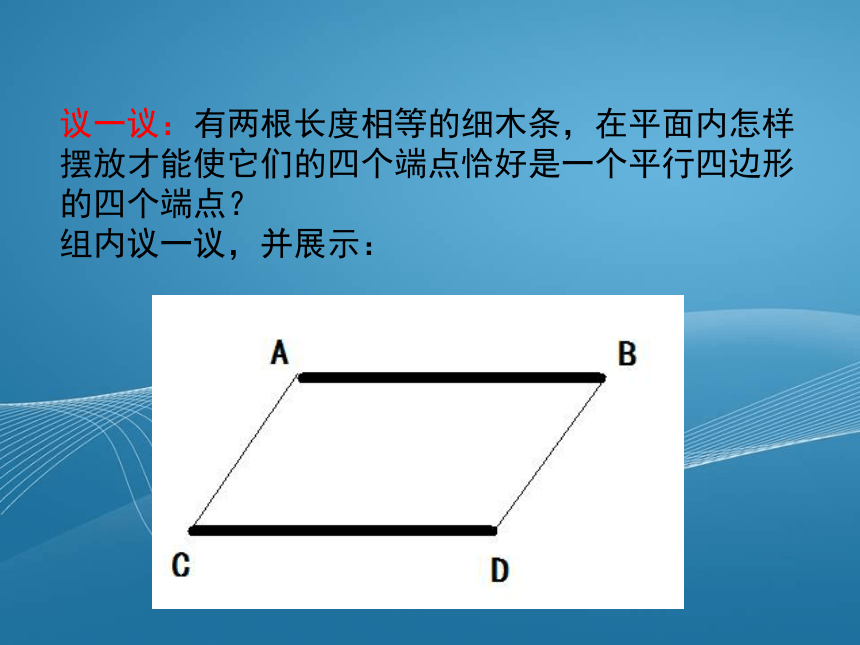
议一议:有两根长度相等的细木条,在平面内怎样摆放才能使它们的四个端点恰好是一个平行四边形的四个端点?
组内议一议,并展示:
引例:已知:如图,在四边形ABCD中,AB∥CD,AB=CD.
求证:四边形ABCD是平行四边形.
【分析】要证明四边形ABCD是平行四
边形.可转化证明两组对边分别相
等,从而作辅助线,用全等三角形来证明
相应的边相等.
证明:连接AC. ∵ AB∥CD,
∴ ∠1=∠2.∵AB=CD,AC=CA,
∴△ABC≌△CDA(SAS).
∴BC=DA.∴四边形ABCD是平行四边形.
B
D
C
A
1
2
【定理】一组对边平行且相等的四边形是平行四边形.
例、已知:如图,在 □ ABCD中,点M、N分别在AD和BC上,点E、F在BD上,且DM=BN,DF=BE
求证:四边形MENF是平行四边形
A
B
C
D
E
F
M
N
证明:∵四边形ABCD是平行四边形,
∴AD∥ BC(平行四边形的定义)
∴∠MDF=∠NBE.
∵DM=BN,DF=BE,
∴△MDF≌△NBE.
∴MF=NE,∠MFD=∠NEB.
∴∠MFE=∠NEF.
∴MF∥ NE.
∴四边形MENF是平行四边形(一组对
边平行且相等的四边形是平行四边形)。
A
B
C
D
E
F
M
N
变式1:已知:如图,在 ABCD中,E,F是对角线BD上的两点,且BE=DF.M,N分别是AD和BC边上的中点. 求证:四边形ENFM是平行四边形。
A
B
C
D
E
F
M
N
变式2:已知:如图,E,F是 ABCD的对角线BD上的两点,且∠BAE=∠DCF 求证:四边形AECF是平行四边形。
A
B
C
D
E
F
O
变式3:已知:如图,在 ABCD中,∠BAD和∠BCD的平分线AE、CF分别与对角线BD相交于点E,F。 求证:四边形AECF是平行四边形。
A
B
C
D
E
F
已知:如图,在□ABCD中,BF=DE.
求证:四边形AFCE是平行四边形.
分析:由已知的平行四边形和
BF=DE可知,CE=AF,则转化为利用
一组对边平行且相等来证明.
证明:∵四边形ABCD是平行四边形,
∴DC∥AB,DC=AB.
∵ DE=BF,∴CE=AF,
∴四边形AFCE是平行四边形.
A
B
C
D
E
F
做一做:如图,以方格纸的格点为顶点用直尺画出三个平行四边形,并说明你画图的方法和其中的道理。
说能出你这节课的收获和体验让大家与你分享吗?
定义: 两组对边分别平行的四边形是 平行四边形.
定理1:两组对边分别相等的四边形是平行四边形.
定理2: 一组对边平行且相等的四边形 平行四边形 .
现在我们已经学过平行四边形的判定方法:
5.2.2平行四边形的判定
教学目标
知识技能目标
1.运用类比的方法,通过学生的合作探究,得出平行四边形的判定方法.
2.理解一组对边平行且相等的四边形是平行四边形这一判定定理,并学会简单运用.
过程与方法目标
1.经历平行四边行判别条件的探索过程,在探究活动中发展学生的合情推理意识.
2.在运用平行四边形的判定方法解决问题的过程中,进一步培养和发展学生的逻辑思维能力和推理论证的几何表达能力.
教学重点:平行四边形判定方法的综合运用.
教学难点:平行四边形的性质和判定的综合运用.
定理1:两组对边分别相等的四边形是平行四边形
说一说:我们已经学过平行四边形的哪些判定方法
定义: 两组对边分别平行的四边形是平行四边形
两组对角分别相等的四边形是平行四边形.
议一议:有两根长度相等的细木条,在平面内怎样摆放才能使它们的四个端点恰好是一个平行四边形的四个端点?
组内议一议,并展示:
引例:已知:如图,在四边形ABCD中,AB∥CD,AB=CD.
求证:四边形ABCD是平行四边形.
【分析】要证明四边形ABCD是平行四
边形.可转化证明两组对边分别相
等,从而作辅助线,用全等三角形来证明
相应的边相等.
证明:连接AC. ∵ AB∥CD,
∴ ∠1=∠2.∵AB=CD,AC=CA,
∴△ABC≌△CDA(SAS).
∴BC=DA.∴四边形ABCD是平行四边形.
B
D
C
A
1
2
【定理】一组对边平行且相等的四边形是平行四边形.
例、已知:如图,在 □ ABCD中,点M、N分别在AD和BC上,点E、F在BD上,且DM=BN,DF=BE
求证:四边形MENF是平行四边形
A
B
C
D
E
F
M
N
证明:∵四边形ABCD是平行四边形,
∴AD∥ BC(平行四边形的定义)
∴∠MDF=∠NBE.
∵DM=BN,DF=BE,
∴△MDF≌△NBE.
∴MF=NE,∠MFD=∠NEB.
∴∠MFE=∠NEF.
∴MF∥ NE.
∴四边形MENF是平行四边形(一组对
边平行且相等的四边形是平行四边形)。
A
B
C
D
E
F
M
N
变式1:已知:如图,在 ABCD中,E,F是对角线BD上的两点,且BE=DF.M,N分别是AD和BC边上的中点. 求证:四边形ENFM是平行四边形。
A
B
C
D
E
F
M
N
变式2:已知:如图,E,F是 ABCD的对角线BD上的两点,且∠BAE=∠DCF 求证:四边形AECF是平行四边形。
A
B
C
D
E
F
O
变式3:已知:如图,在 ABCD中,∠BAD和∠BCD的平分线AE、CF分别与对角线BD相交于点E,F。 求证:四边形AECF是平行四边形。
A
B
C
D
E
F
已知:如图,在□ABCD中,BF=DE.
求证:四边形AFCE是平行四边形.
分析:由已知的平行四边形和
BF=DE可知,CE=AF,则转化为利用
一组对边平行且相等来证明.
证明:∵四边形ABCD是平行四边形,
∴DC∥AB,DC=AB.
∵ DE=BF,∴CE=AF,
∴四边形AFCE是平行四边形.
A
B
C
D
E
F
做一做:如图,以方格纸的格点为顶点用直尺画出三个平行四边形,并说明你画图的方法和其中的道理。
说能出你这节课的收获和体验让大家与你分享吗?
定义: 两组对边分别平行的四边形是 平行四边形.
定理1:两组对边分别相等的四边形是平行四边形.
定理2: 一组对边平行且相等的四边形 平行四边形 .
现在我们已经学过平行四边形的判定方法:
