2023-2024学年人教版数学八年级上册单元闯关双测卷第十一章 三角形(测基础)(含解析)
文档属性
| 名称 | 2023-2024学年人教版数学八年级上册单元闯关双测卷第十一章 三角形(测基础)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 528.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-15 00:00:00 | ||
图片预览




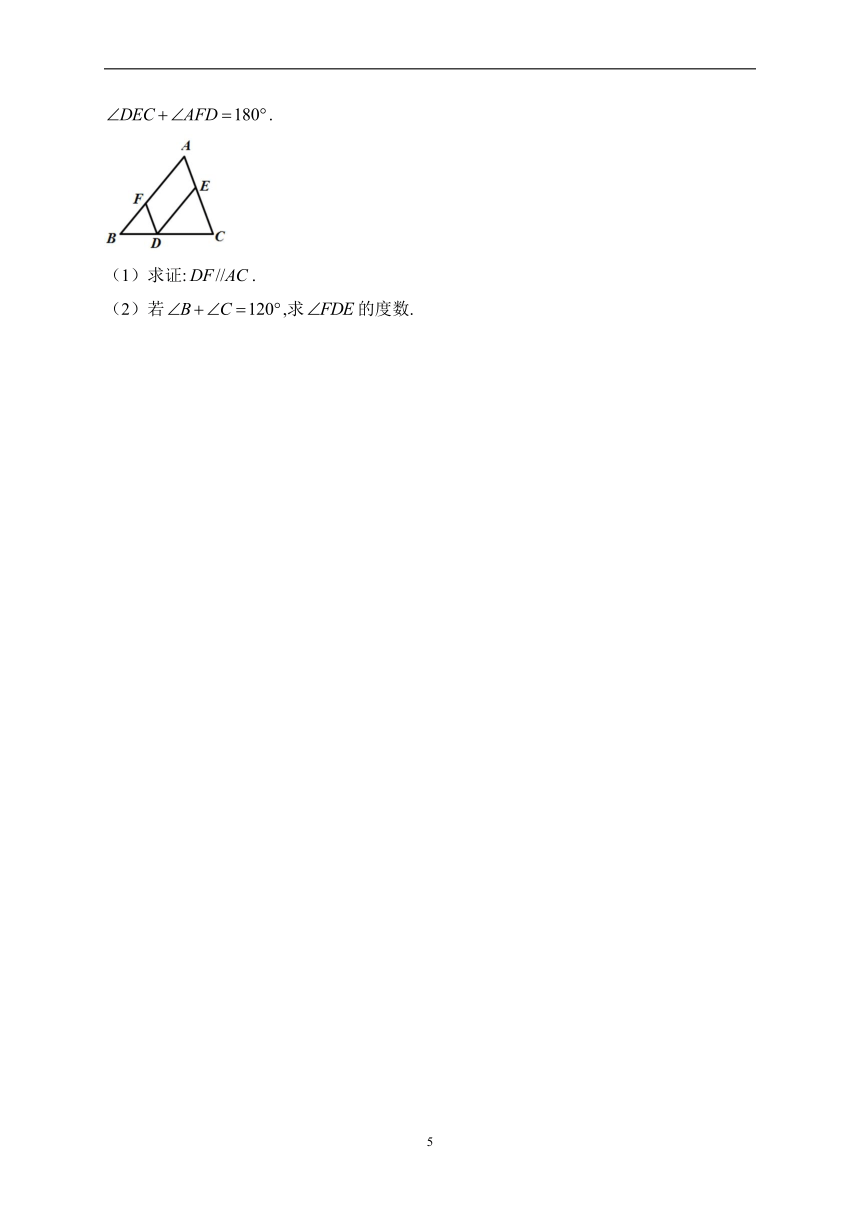
文档简介
第十一章 三角形(测基础)——2023-2024学年人教版数学八年级上册单元闯关双测卷
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.如图所示,图中可以用一个字母表示的角有( )
A.1个 B.2个 C.3个 D.4个
2.为估计池塘两岸A、B间的距离,如图,小明在池塘一侧选取了一点O,测得,,那么AB的距离不可能是( )
A.5m B.15m C.20m D.30m
3.三角形的下列四种线段中一定能将三角形分成面积相等的两部分的是( )
A.角平分线 B.中位线 C.高 D.中线
4.利用直角三角板,作的高,下列作法正确的是( )
A. B. C. D.
5.如图,已知,,则( )
A. B. C. D.
6.如图,在中,AE是高,BD是角平分线,CF是中线,下列说法不正确的是( )
A. B.
C. D.
7.如图,在中,和的平分线相交于点D,若,则的度数为( )
A. B. C. D.
8.下列说法错误的是( )
A.直角三角形只有一条高线.
B.钝角三角形有两条高线在三角形的外部.
C.任意三角形都有三条高线、中线、角平分线.
D.锐角三角形的三条高线、三条中线、三条角平分线分别交于一点.
9.如图, 两条平行的直线a,b 分别过正六边形ABCDEF 的顶点A,E, 且直线b 与BC 交于点G,, 则 的度数为( )
A. B. C. D.
10.已知直线,将一块含30°角的直角三角板ABC(,)按如图方式放置,点A,B分别落在直线m,n上.若.则的度数为( )
A.30° B.40° C.60° D.70°
二、填空题(每小题4分,共20分)
11.图是李老师去某地旅游拍摄的“山谷中的铁架桥”,铁架桥框架做成了三角形的形状,该设计是利用三角形的____________.
12.已知三角形的两边长分别为1和4,第三边长为x,则第三边长的范围为________.
13.已知一个多边形的每一个外角等于,则它的内角和等于______.
14.如图所示,AD是的中线,E是AD的中点,连接CE,若,则__________.
15.如图,,,,则等于________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)已知一个多边形的内角和与外角和的比为2:1,求这个多边形的对角线条数.
17.(8分)已知(如图),按下列要求画图:
(1)画出的中线AD;
(2)画出的角平分线DM;
(3)画出的高线CN;
(4)若(,分别表示与的周长),且,则___________.
18.(10分)已知的三条边长分别为,.
(1)用含x,y的代数式表示的周长L.
(2)从以下三组数据中选择合适的一组, 计算的周长L的值. 第一组:,;
第二组:,;
第三组:,.
19.(10分)如图,在中,,,.
(1)求的度数;
(2)若,求的度数.
20.(12分)如图所示,求的度数.
21.(12分)如图,D是BC上一点,,交AC于点E,F是AB上一点,且.
(1)求证:.
(2)若,求的度数.
答案以及解析
1.答案:B
解析:能用一个字母表示的角有2个:,;故选B.
2.答案:D
解析:根据三角形三边关系得,
即,
所以AB的距离不能是30m.
故选:D.
3.答案:D
解析:A、三角形的角平分线把三角形分成两部分,这两部分的面积比分情况而定;(下图中两部分面积显然不等)
B、三角形的中位线把三角形分成两部分,这两部分的面积经计算得:三角形面积为梯形面积的;
C、三角形的高把三角形分成两部分,这两部分的面积比分情况而定;(下图中两部分面积显然不等)
D、三角形的中线AD把三角形分成两部分,的面积为,面积为;
因为AD为中线,所以D为BC中点,所以,
所以的面积等于的面积.
三角形的中线把三角形分成面积相等的两部分.
故选:D.
4.答案:D
解析:A,B,C均不高线.故选:D.
5.答案:D
解析:,
,
.故选D.
6.答案:A
解析:当CF是角平分线时,一定成立,但是CF是中线,所以A选项说法错误;因为BD是角平分线,所以,故B选项说法正确;因为AE是高,所以,故C选项说法正确;因为CF是中线,所以点F是AB边的中点,即,故D选项说法正确.
7.答案:B
解析:如图,,
.
,的平分线相交于点E,
,.
8.答案:A
解析:A、直角三角形有三条高线,选项说法错误,符合题意;
B、钝角三角形有两条高线在三角形的外部,选项说法正确,不符合题意;
C、任意三角形都有三条高线、中线、角平分线,选项说法正确,不符合题意;
D、锐角三角形的三条高线、三条中线、三条角平分线分别交于一点,选项说法正确,不符合题意;故选A.
9.答案:C
解析:连接BE, 易得, 又 直线, , 多边形 ABCDEF是正六边形, ,,
10.答案:B
解析:,,
,
,
,故选B.
11.答案:稳定性
解析:铁架桥框架做成三角形是因为三角形具有稳定性.
12.答案:
解析:由题意得,
解得,
故答案为:.
13.答案:
解析:多边形边数为:,
则这个多边形是六边形;
内角和是:.
故答案为:.
14.答案:1
解析:AD是的中线,,E是AD的中点,.
15.答案:20°
解析:,,
,
,,
,
.
故答案为:20°.
16.答案:设这个多边形的边数为n,
由题意,得,解得,
所以这个多边形的对角线条数为.
17.解析:(1)如图,AD为所作.
(2)如图,DM为所作.
(3)如图,CN为所作.
(4)为的中线,
.
,
,
.
,
.
18.解析:(1)
(2) 当 时, , 不合题意.
当 ,时, ,,,
故边长分别为1,3,5 的三条边不能构成三角形.
当 ,时,,.
若三条边长分别为3,6,5,
则这三条边满足三角形三边关系,
故
19.解析:(1),,,
,
,.
.
(2),,
,,
,
20.答案:如图,连接BE,则.
21.答案:解析:(1)证明:,
.
,
.
.
(2),.
,.
,
2
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.如图所示,图中可以用一个字母表示的角有( )
A.1个 B.2个 C.3个 D.4个
2.为估计池塘两岸A、B间的距离,如图,小明在池塘一侧选取了一点O,测得,,那么AB的距离不可能是( )
A.5m B.15m C.20m D.30m
3.三角形的下列四种线段中一定能将三角形分成面积相等的两部分的是( )
A.角平分线 B.中位线 C.高 D.中线
4.利用直角三角板,作的高,下列作法正确的是( )
A. B. C. D.
5.如图,已知,,则( )
A. B. C. D.
6.如图,在中,AE是高,BD是角平分线,CF是中线,下列说法不正确的是( )
A. B.
C. D.
7.如图,在中,和的平分线相交于点D,若,则的度数为( )
A. B. C. D.
8.下列说法错误的是( )
A.直角三角形只有一条高线.
B.钝角三角形有两条高线在三角形的外部.
C.任意三角形都有三条高线、中线、角平分线.
D.锐角三角形的三条高线、三条中线、三条角平分线分别交于一点.
9.如图, 两条平行的直线a,b 分别过正六边形ABCDEF 的顶点A,E, 且直线b 与BC 交于点G,, 则 的度数为( )
A. B. C. D.
10.已知直线,将一块含30°角的直角三角板ABC(,)按如图方式放置,点A,B分别落在直线m,n上.若.则的度数为( )
A.30° B.40° C.60° D.70°
二、填空题(每小题4分,共20分)
11.图是李老师去某地旅游拍摄的“山谷中的铁架桥”,铁架桥框架做成了三角形的形状,该设计是利用三角形的____________.
12.已知三角形的两边长分别为1和4,第三边长为x,则第三边长的范围为________.
13.已知一个多边形的每一个外角等于,则它的内角和等于______.
14.如图所示,AD是的中线,E是AD的中点,连接CE,若,则__________.
15.如图,,,,则等于________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)已知一个多边形的内角和与外角和的比为2:1,求这个多边形的对角线条数.
17.(8分)已知(如图),按下列要求画图:
(1)画出的中线AD;
(2)画出的角平分线DM;
(3)画出的高线CN;
(4)若(,分别表示与的周长),且,则___________.
18.(10分)已知的三条边长分别为,.
(1)用含x,y的代数式表示的周长L.
(2)从以下三组数据中选择合适的一组, 计算的周长L的值. 第一组:,;
第二组:,;
第三组:,.
19.(10分)如图,在中,,,.
(1)求的度数;
(2)若,求的度数.
20.(12分)如图所示,求的度数.
21.(12分)如图,D是BC上一点,,交AC于点E,F是AB上一点,且.
(1)求证:.
(2)若,求的度数.
答案以及解析
1.答案:B
解析:能用一个字母表示的角有2个:,;故选B.
2.答案:D
解析:根据三角形三边关系得,
即,
所以AB的距离不能是30m.
故选:D.
3.答案:D
解析:A、三角形的角平分线把三角形分成两部分,这两部分的面积比分情况而定;(下图中两部分面积显然不等)
B、三角形的中位线把三角形分成两部分,这两部分的面积经计算得:三角形面积为梯形面积的;
C、三角形的高把三角形分成两部分,这两部分的面积比分情况而定;(下图中两部分面积显然不等)
D、三角形的中线AD把三角形分成两部分,的面积为,面积为;
因为AD为中线,所以D为BC中点,所以,
所以的面积等于的面积.
三角形的中线把三角形分成面积相等的两部分.
故选:D.
4.答案:D
解析:A,B,C均不高线.故选:D.
5.答案:D
解析:,
,
.故选D.
6.答案:A
解析:当CF是角平分线时,一定成立,但是CF是中线,所以A选项说法错误;因为BD是角平分线,所以,故B选项说法正确;因为AE是高,所以,故C选项说法正确;因为CF是中线,所以点F是AB边的中点,即,故D选项说法正确.
7.答案:B
解析:如图,,
.
,的平分线相交于点E,
,.
8.答案:A
解析:A、直角三角形有三条高线,选项说法错误,符合题意;
B、钝角三角形有两条高线在三角形的外部,选项说法正确,不符合题意;
C、任意三角形都有三条高线、中线、角平分线,选项说法正确,不符合题意;
D、锐角三角形的三条高线、三条中线、三条角平分线分别交于一点,选项说法正确,不符合题意;故选A.
9.答案:C
解析:连接BE, 易得, 又 直线, , 多边形 ABCDEF是正六边形, ,,
10.答案:B
解析:,,
,
,
,故选B.
11.答案:稳定性
解析:铁架桥框架做成三角形是因为三角形具有稳定性.
12.答案:
解析:由题意得,
解得,
故答案为:.
13.答案:
解析:多边形边数为:,
则这个多边形是六边形;
内角和是:.
故答案为:.
14.答案:1
解析:AD是的中线,,E是AD的中点,.
15.答案:20°
解析:,,
,
,,
,
.
故答案为:20°.
16.答案:设这个多边形的边数为n,
由题意,得,解得,
所以这个多边形的对角线条数为.
17.解析:(1)如图,AD为所作.
(2)如图,DM为所作.
(3)如图,CN为所作.
(4)为的中线,
.
,
,
.
,
.
18.解析:(1)
(2) 当 时, , 不合题意.
当 ,时, ,,,
故边长分别为1,3,5 的三条边不能构成三角形.
当 ,时,,.
若三条边长分别为3,6,5,
则这三条边满足三角形三边关系,
故
19.解析:(1),,,
,
,.
.
(2),,
,,
,
20.答案:如图,连接BE,则.
21.答案:解析:(1)证明:,
.
,
.
.
(2),.
,.
,
2
