27.2.1相似三角形的判定(3)课件
文档属性
| 名称 | 27.2.1相似三角形的判定(3)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 820.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-29 10:33:36 | ||
图片预览

文档简介
课件16张PPT。第二十七章 相似27.2.1第二十七章
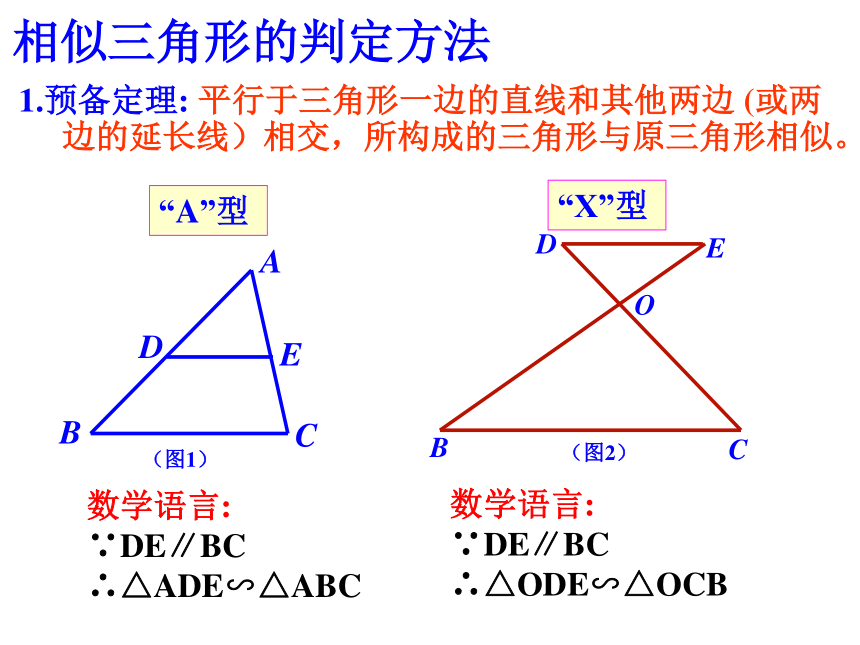
相似三角形的判定(3)相似三角形的判定方法1.预备定理: 平行于三角形一边的直线和其他两边 (或两边的延长线)相交,所构成的三角形与原三角形相似。“A”型 “X”型 数学语言:
∵DE∥BC
∴△ADE∽△ABC数学语言:
∵DE∥BC
∴△ODE∽△OCB2.相似三角形判定定理1:
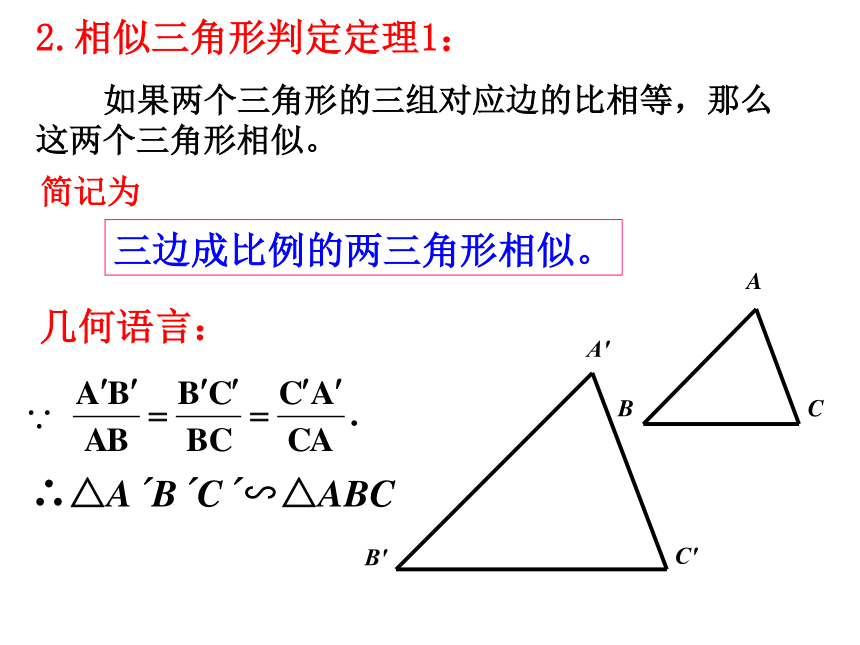
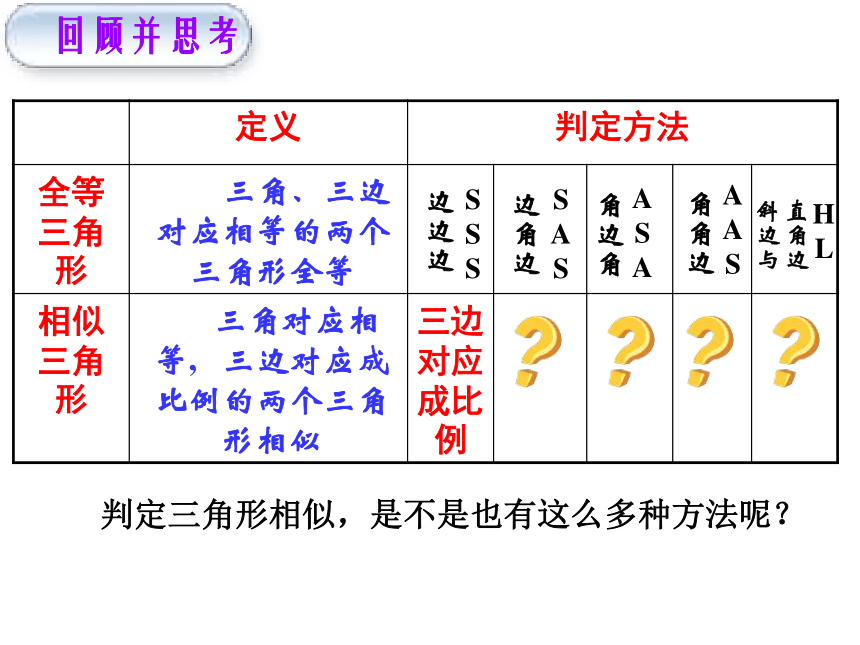
如果两个三角形的三组对应边的比相等,那么这两个三角形相似。几何语言:∴△A′B′C′∽△ABC∵Z.x.x. K 回顾并思考 三角、三边对应相等的两个三角形全等 三角对应相等, 三边对应成比例的两个三角形相似 角边角A
S
A角角边A
A
S边边边S
S
S边角边S
A
SH
L 判定三角形相似,是不是也有这么多种方法呢?直角边
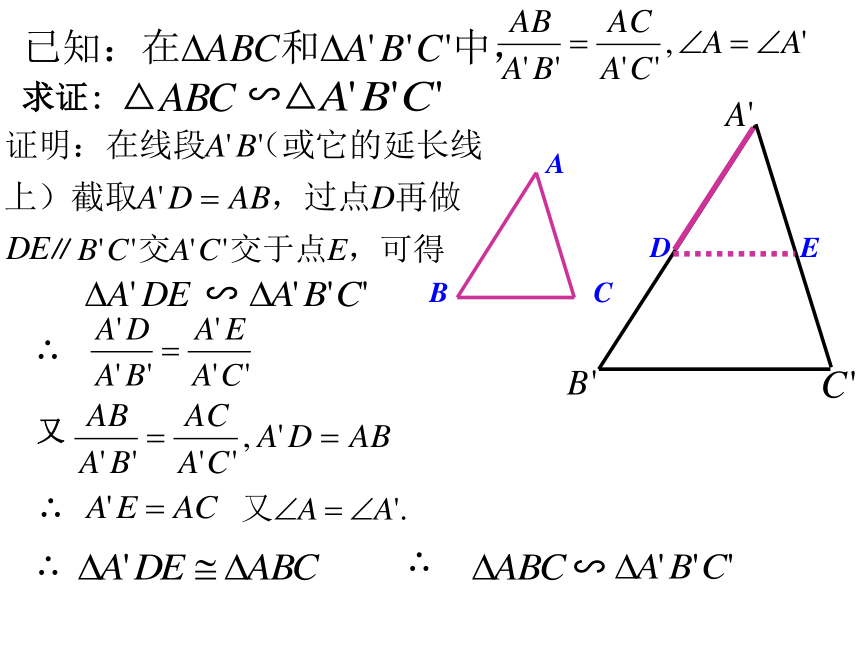
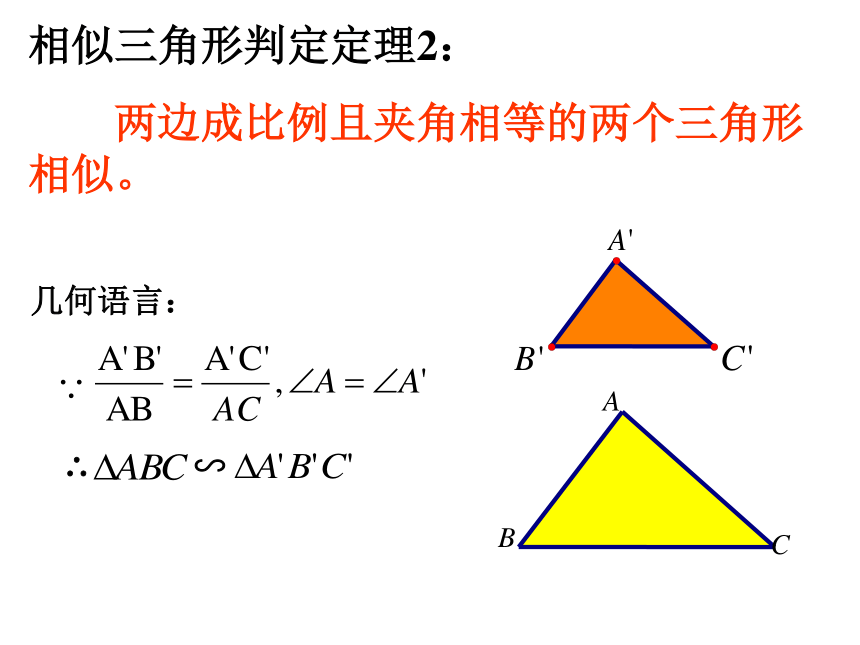
斜边与已知:求证: △∽△求证: △∽△DE∴又∴∴∥∽∽∴相似三角形判定定理2:
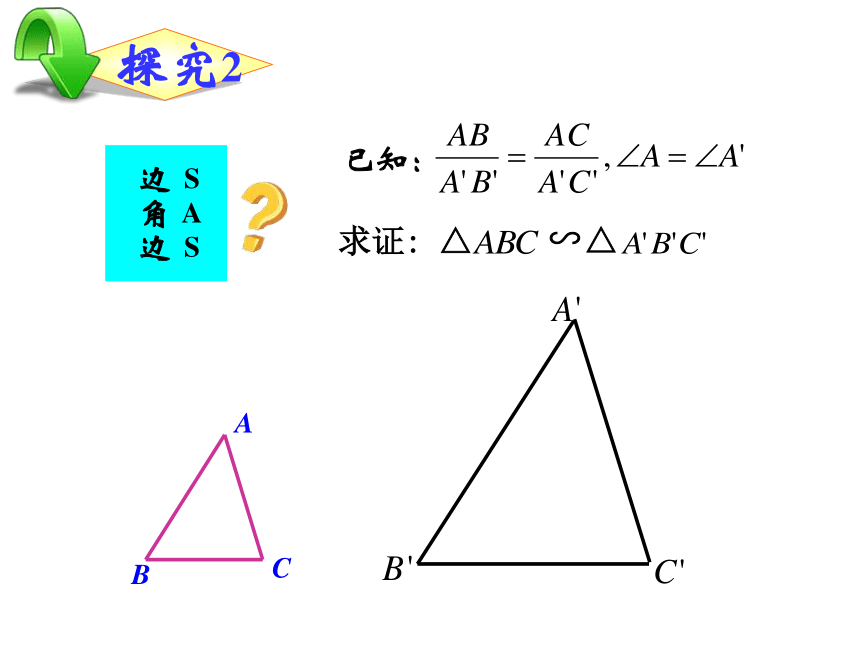
两边成比例且夹角相等的两个三角形相似。∵几何语言:思考?对于△ABC和△A’B’C’, 如果 ,
∠B=∠B’,这两个三角形一定相似吗?试着画画看.例1:根据下列条件,判断△ABC与△A’B’C’是否相似,并说明理由.
(1)∠A=600,AB=7cm,AC=14cm.
∠A’=600,A’B’=3cm,A’C’=6cm.
(2)AB=4 cm,BC=6cm,AC=8cm,
A’B’=12cm,B’C’=18cm,A’C’=21cm.△ABC与△A’B’C‘的三组对应边的比不等,它们不相似.∽要使两三角形相似,不改变的AC长,A’C’的长应改为多少? AB=7, AC=14, ∠A=60°
A’B’=6,A’C’=3, ∠A’= 60°例2:根据下列条件,判断△ABC和△A’B’C’
是否相似,并说明理由。变式3、已知:如图, △ABC∽△ADE 。
求证:△ABD∽△ACE。4、已知:如图,正方形ABCD中,E是AD的中点,F在边DC上,且3DF=FC。求证:BE⊥EF。5、已知如图,AB∥A'B',BC∥B'C' 求证:△ABC∽△A'B'C’中考透视6、如图正方形边长是2,BE=CE,MN=1。线段MN的两端在CD、AD上滑动,当DM为多长时,△ABE与以D、M、N为顶点的三角形相似。N7、已知在△ABC中,∠C=90o ,AC=8cm,BC=6cm,点P从点A出发,沿AC以3厘米/秒的速度向点C移动,点Q从点B出发,沿BA以4厘米/秒的速度向点A移动。
如果P、Q分别从A、B 同时出发,移动时间为t秒 (0
相似三角形的判定(3)相似三角形的判定方法1.预备定理: 平行于三角形一边的直线和其他两边 (或两边的延长线)相交,所构成的三角形与原三角形相似。“A”型 “X”型 数学语言:
∵DE∥BC
∴△ADE∽△ABC数学语言:
∵DE∥BC
∴△ODE∽△OCB2.相似三角形判定定理1:
如果两个三角形的三组对应边的比相等,那么这两个三角形相似。几何语言:∴△A′B′C′∽△ABC∵Z.x.x. K 回顾并思考 三角、三边对应相等的两个三角形全等 三角对应相等, 三边对应成比例的两个三角形相似 角边角A
S
A角角边A
A
S边边边S
S
S边角边S
A
SH
L 判定三角形相似,是不是也有这么多种方法呢?直角边
斜边与已知:求证: △∽△求证: △∽△DE∴又∴∴∥∽∽∴相似三角形判定定理2:
两边成比例且夹角相等的两个三角形相似。∵几何语言:思考?对于△ABC和△A’B’C’, 如果 ,
∠B=∠B’,这两个三角形一定相似吗?试着画画看.例1:根据下列条件,判断△ABC与△A’B’C’是否相似,并说明理由.
(1)∠A=600,AB=7cm,AC=14cm.
∠A’=600,A’B’=3cm,A’C’=6cm.
(2)AB=4 cm,BC=6cm,AC=8cm,
A’B’=12cm,B’C’=18cm,A’C’=21cm.△ABC与△A’B’C‘的三组对应边的比不等,它们不相似.∽要使两三角形相似,不改变的AC长,A’C’的长应改为多少? AB=7, AC=14, ∠A=60°
A’B’=6,A’C’=3, ∠A’= 60°例2:根据下列条件,判断△ABC和△A’B’C’
是否相似,并说明理由。变式3、已知:如图, △ABC∽△ADE 。
求证:△ABD∽△ACE。4、已知:如图,正方形ABCD中,E是AD的中点,F在边DC上,且3DF=FC。求证:BE⊥EF。5、已知如图,AB∥A'B',BC∥B'C' 求证:△ABC∽△A'B'C’中考透视6、如图正方形边长是2,BE=CE,MN=1。线段MN的两端在CD、AD上滑动,当DM为多长时,△ABE与以D、M、N为顶点的三角形相似。N7、已知在△ABC中,∠C=90o ,AC=8cm,BC=6cm,点P从点A出发,沿AC以3厘米/秒的速度向点C移动,点Q从点B出发,沿BA以4厘米/秒的速度向点A移动。
如果P、Q分别从A、B 同时出发,移动时间为t秒 (0
