27.2.1相似三角形的判定(4)课件
文档属性
| 名称 | 27.2.1相似三角形的判定(4)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 795.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-29 00:00:00 | ||
图片预览



文档简介
课件18张PPT。第二十七章 相似27.2.1第二十七章
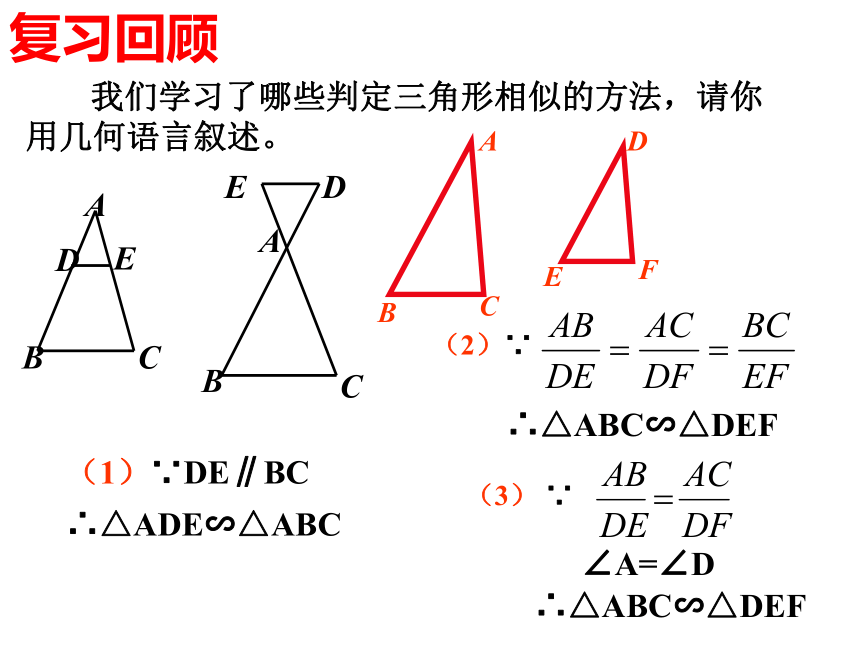
相似三角形的判定(4)(1)∵DE∥BC
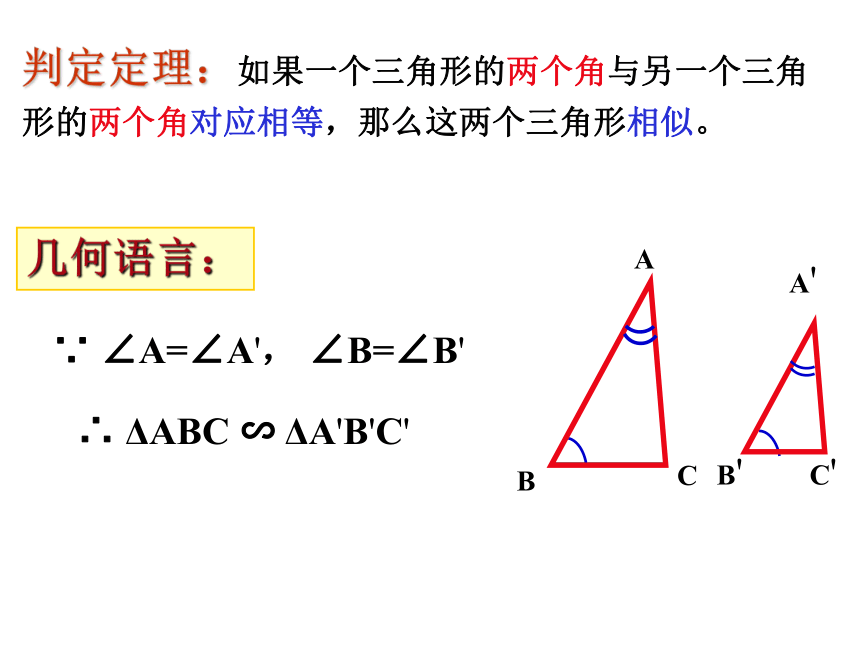
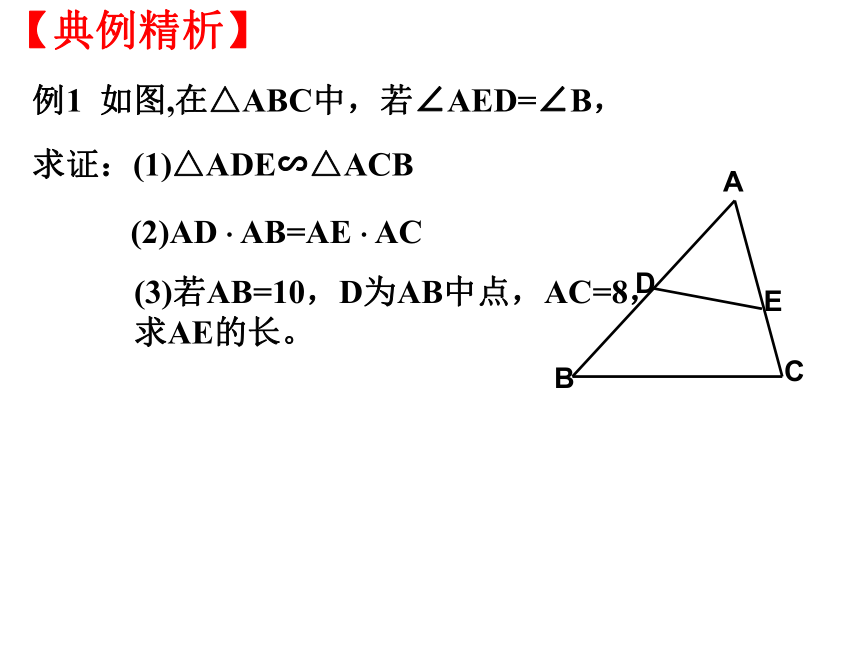
∴△ADE∽△ABC 我们学习了哪些判定三角形相似的方法,请你用几何语言叙述。复习回顾∴△ABC∽△DEF∠A=∠D∴△ABC∽△DEF观察: 观察两个含30°角的三角尺。 一般地,如果两个三角形有两组对应角相等,它们一定相似吗?发现:两个三角尺大小不同,但它们看起来是相似的。问题:已知:在△ABC 和△ 中, ∠A=∠A', ∠B'=∠B求证: ΔA'B'C'∽ΔABCDECC'∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'几何语言:判定定理:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。【典例精析】例1 如图,在△ABC中,若∠AED=∠B,
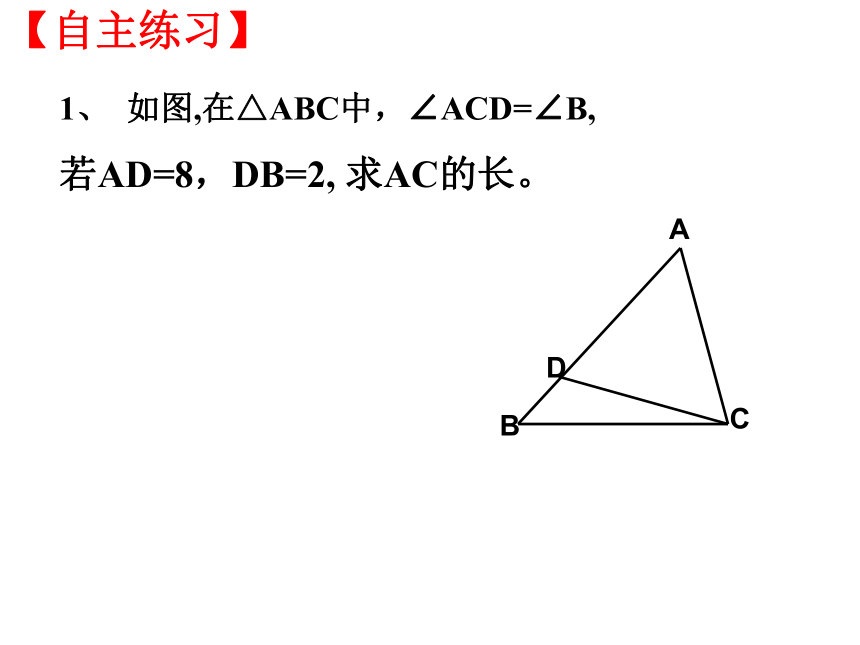
求证:(1)△ADE∽△ACB(2)AD . AB=AE . AC(3)若AB=10,D为AB中点,AC=8,求AE的长。【自主练习】1、 如图,在△ABC中,∠ACD=∠B,
若AD=8,DB=2, 求AC的长。
例2 如图,弦AB和CD相交于圆O内一点P。
求证:PA ? PB = PC?PD【典例精析】你能证明吗?【自主练习】PA ? PB = PC?PD例3 求证:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。已知:在RtΔABC中,CD是斜边AB上的高。证明: ∵ ∠A=∠A,∠ADC=∠ACB=900,∴ ΔACD∽ΔABC(两角对应相等,两 三角形相似)。同理 ΔCBD ∽ ΔABC 。∴ ΔABC∽ΔCBD∽ΔACD。求证:求证:(1)AC2=AD · AB;求证:(2)CD2=AD · DB引申【典例精析】BC2=BD · AB请记住以上结论18【自主练习】┓282、如图,点C是半圆的直径AB上的一点,CD⊥AB,垂足为D,若AC=2,AB=10,求CD的长总结反思 与大家分享一下本节课你的收获! 3、学会了利用相似证明等积式1、学习了两角相等证相似2、认识了三个相似基本图4、体会到等量代换在等积式证明中的作用例4. 如图,在正方形ABCD中,点E为DB上一点,AE的延长线交DC于F,交BC的延长线于G。
试说明AE2=EF . EG。【拓展提高】E提问1:有一个锐角相等的两个直角三角形是否相似?提问2:一个直角三角形的两条直角边和另一个直角三角形的两条直角边对应成比例,这两个直角三角形是否相似? 提问3:如果把提问2中的条件改为一条斜边和一条直角边对应成比例呢? 一个锐角对应相等的两个直角三角形相似.两条对应的直角边的比相等的两个直角三角形相似. 如果两个直角三角形的斜边的比和另一个对应的直角边的比相等,那么这两个直角三角形相似.【拓展提高】例2已知:如图,Rt △ABC中,CD是斜边上的高求证: △ABC∽ △CBD∽△ACD【拓展提高】 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。三角形相似的识别方法有那些?方法1:通过定义方法5:通过两角对应相等。方法6:斜边直角边对应成比例方法2:平行于三角形一边的直线。方法3:三边对应成比例。方法4:两边对应成比例且夹角。【方法小结】基础演练1、下列图形中两个三角形是否相似?(1)(2)(3)(4)Zx.xk 2、判断题:
⑴ 所有的直角三角形都相似 .( )
⑵ 所有的等边三角形都相似. ( )
⑶ 所有的等腰直角三角形都相似. ( )
⑷ 有一个角相等的两等腰三角形相似 . ( )
×√√×
相似三角形的判定(4)(1)∵DE∥BC
∴△ADE∽△ABC 我们学习了哪些判定三角形相似的方法,请你用几何语言叙述。复习回顾∴△ABC∽△DEF∠A=∠D∴△ABC∽△DEF观察: 观察两个含30°角的三角尺。 一般地,如果两个三角形有两组对应角相等,它们一定相似吗?发现:两个三角尺大小不同,但它们看起来是相似的。问题:已知:在△ABC 和△ 中, ∠A=∠A', ∠B'=∠B求证: ΔA'B'C'∽ΔABCDECC'∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'几何语言:判定定理:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。【典例精析】例1 如图,在△ABC中,若∠AED=∠B,
求证:(1)△ADE∽△ACB(2)AD . AB=AE . AC(3)若AB=10,D为AB中点,AC=8,求AE的长。【自主练习】1、 如图,在△ABC中,∠ACD=∠B,
若AD=8,DB=2, 求AC的长。
例2 如图,弦AB和CD相交于圆O内一点P。
求证:PA ? PB = PC?PD【典例精析】你能证明吗?【自主练习】PA ? PB = PC?PD例3 求证:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。已知:在RtΔABC中,CD是斜边AB上的高。证明: ∵ ∠A=∠A,∠ADC=∠ACB=900,∴ ΔACD∽ΔABC(两角对应相等,两 三角形相似)。同理 ΔCBD ∽ ΔABC 。∴ ΔABC∽ΔCBD∽ΔACD。求证:求证:(1)AC2=AD · AB;求证:(2)CD2=AD · DB引申【典例精析】BC2=BD · AB请记住以上结论18【自主练习】┓282、如图,点C是半圆的直径AB上的一点,CD⊥AB,垂足为D,若AC=2,AB=10,求CD的长总结反思 与大家分享一下本节课你的收获! 3、学会了利用相似证明等积式1、学习了两角相等证相似2、认识了三个相似基本图4、体会到等量代换在等积式证明中的作用例4. 如图,在正方形ABCD中,点E为DB上一点,AE的延长线交DC于F,交BC的延长线于G。
试说明AE2=EF . EG。【拓展提高】E提问1:有一个锐角相等的两个直角三角形是否相似?提问2:一个直角三角形的两条直角边和另一个直角三角形的两条直角边对应成比例,这两个直角三角形是否相似? 提问3:如果把提问2中的条件改为一条斜边和一条直角边对应成比例呢? 一个锐角对应相等的两个直角三角形相似.两条对应的直角边的比相等的两个直角三角形相似. 如果两个直角三角形的斜边的比和另一个对应的直角边的比相等,那么这两个直角三角形相似.【拓展提高】例2已知:如图,Rt △ABC中,CD是斜边上的高求证: △ABC∽ △CBD∽△ACD【拓展提高】 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。三角形相似的识别方法有那些?方法1:通过定义方法5:通过两角对应相等。方法6:斜边直角边对应成比例方法2:平行于三角形一边的直线。方法3:三边对应成比例。方法4:两边对应成比例且夹角。【方法小结】基础演练1、下列图形中两个三角形是否相似?(1)(2)(3)(4)Zx.xk 2、判断题:
⑴ 所有的直角三角形都相似 .( )
⑵ 所有的等边三角形都相似. ( )
⑶ 所有的等腰直角三角形都相似. ( )
⑷ 有一个角相等的两等腰三角形相似 . ( )
×√√×
