27.2.3相似三角形的应用举例课件
文档属性
| 名称 | 27.2.3相似三角形的应用举例课件 |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-29 10:47:40 | ||
图片预览





文档简介
课件22张PPT。第二十七章 相似27.2.3
相似三角形的应用举例读万卷书,行万里路1.定义: (对应角、对应边):三个角对应相等,三条边对应成比例的两个三角形相似。
2.预备定理(平行法):平行于三角形一边的直线与其他两边相交,所截得的三角形与原三角形相似。
3.判定定理一(边边边):三边成比例的两个三角形相似。
4.判定定理二(边角边):两边成比例且夹角相等的两个三角形相似。
5.判定定理三(角角):两角分别相等的两个三角形相似。
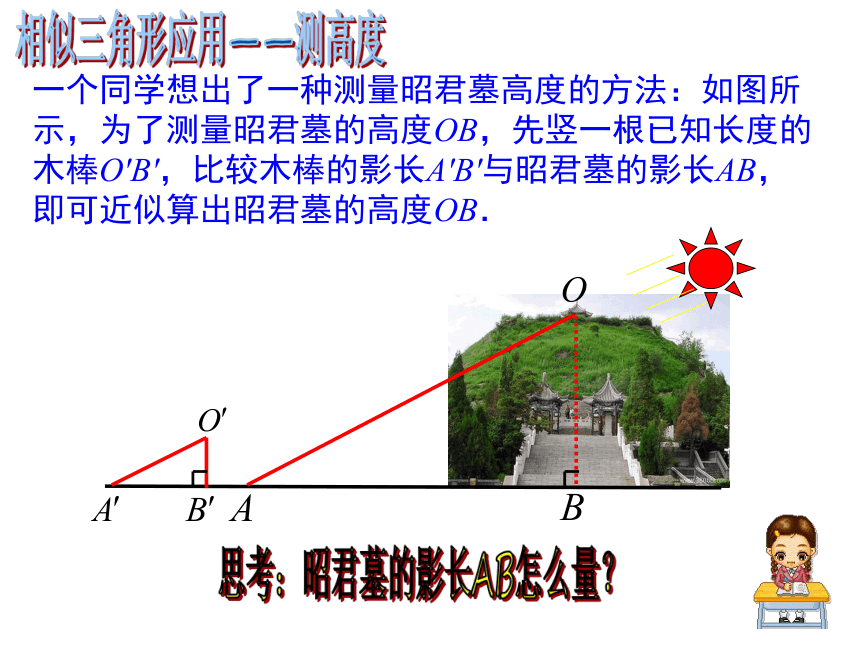
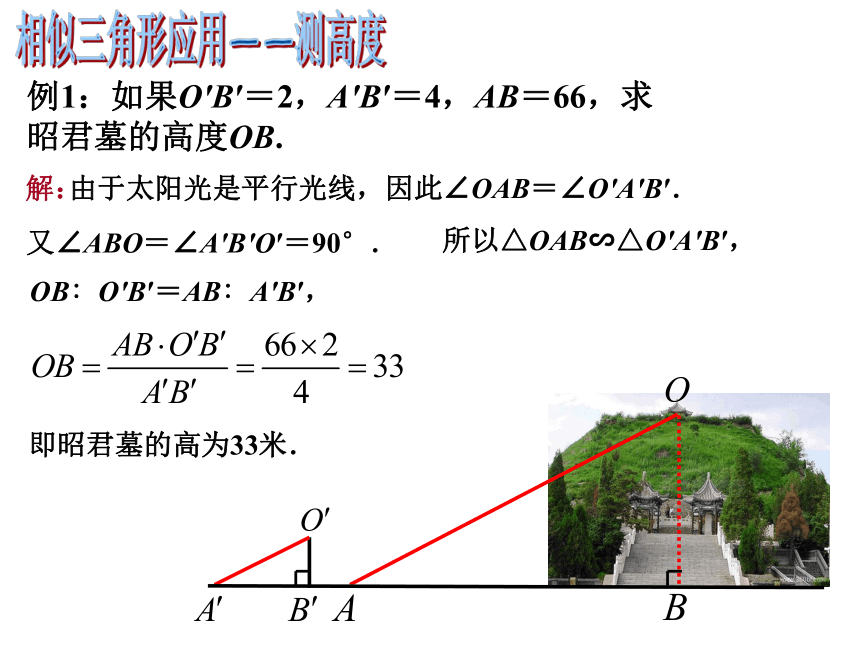
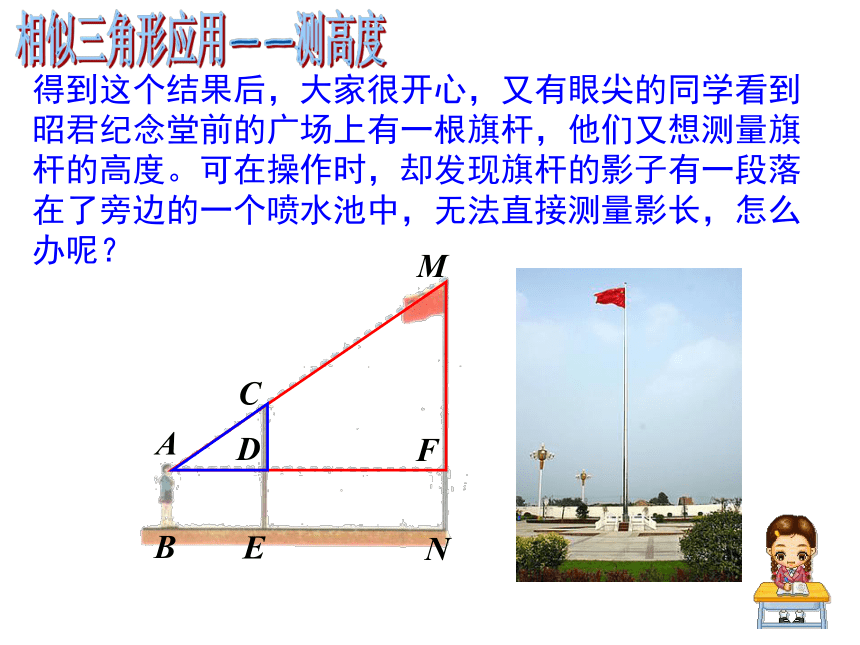
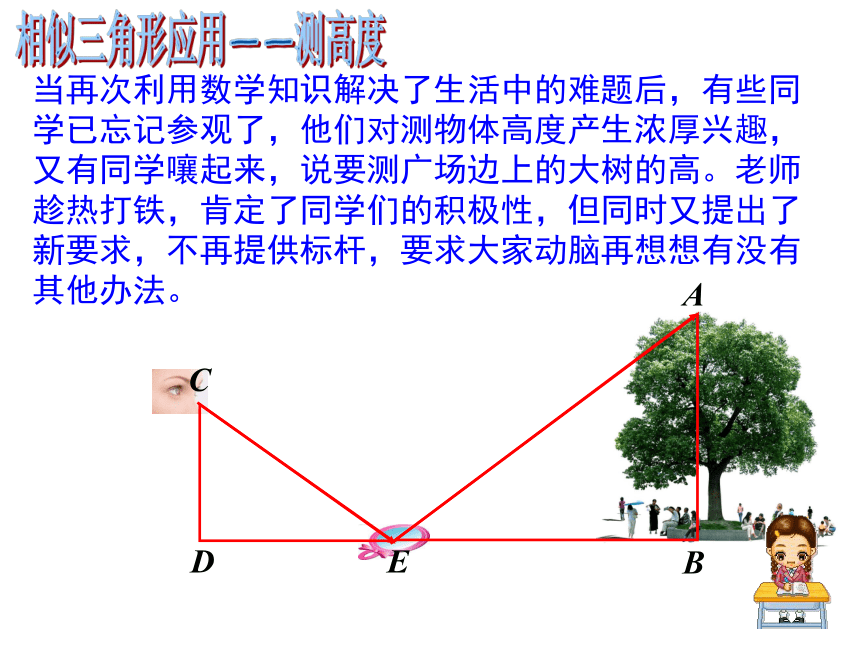
6.判定结论(HL):斜边与直角边成比例的两个直角三角形相似。一 、判断两三角形相似有哪些方法?二、相似三角形有什么性质?对应角相等,对应线段的比相等三、相似三角形可以解决哪些实际问题?相似三角形的应用昭君墓位于呼和浩特南郊9公里处的大黑河畔,是后人追慕和纪念王昭君的遗迹。坐落在呼市南郊的昭君墓,是塞外影响最大的一座昭君墓,整体占地面积近100亩,墓身呈台体状,墓顶建有一座凉亭,墓地东侧是历代名人为昭君墓题写的碑文,西侧是文物陈列室。 我们去旅行:内蒙昭君墓相似三角形应用——测高度在一个艳阳高照的上午,老师带领同学们来到昭君纪念陵,同学四处参观着。其间,有同学提出一个问题,这个昭君墓究竟有多高呢?这个问题引起了大家的兴趣。给你一条2米高的木杆,一把皮尺.你能利用所学知识来测出整个墓高吗?相似三角形应用——测高度我们去旅行:一个同学想出了一种测量昭君墓高度的方法:如图所示,为了测量昭君墓的高度OB,先竖一根已知长度的木棒O′B′,比较木棒的影长A′B′与昭君墓的影长AB,即可近似算出昭君墓的高度OB.相似三角形应用——测高度思考:昭君墓的影长AB怎么量?解: 由于太阳光是平行光线,因此∠OAB=∠O′A′B′. 又∠ABO=∠A′B′O′=90°.所以△OAB∽△O′A′B′,OB∶O′B′=AB∶A′B′,即昭君墓的高为33米.例1:如果O′B′=2,A′B′=4,AB=66,求昭君墓的高度OB.相似三角形应用——测高度相似三角形应用——测高度得到这个结果后,大家很开心,又有眼尖的同学看到昭君纪念堂前的广场上有一根旗杆,他们又想测量旗杆的高度。可在操作时,却发现旗杆的影子有一段落在了旁边的一个喷水池中,无法直接测量影长,怎么办呢?相似三角形应用——测高度当再次利用数学知识解决了生活中的难题后,有些同学已忘记参观了,他们对测物体高度产生浓厚兴趣,又有同学嚷起来,说要测广场边上的大树的高。老师趁热打铁,肯定了同学们的积极性,但同时又提出了新要求,不再提供标杆,要求大家动脑再想想有没有其他办法。归纳:相似应用——测高度利用相似三角形的性质解决实际测高问题的核心是构造相似三角形,在构造的三角形中被测物体必须是其中的一边。常用方法:(1)利用阳光下的影子(△ABC∽ △DEF) (2)利用标杆(△AEC∽ △AFM) (3)利用镜子的反射(△ABC∽ △DEC)
例2:如图,在距离昭君墓186公里的鄂尔多斯响沙湾是国家5A级旅游景区。景区内有一条水流湍急的小河,有同学想要知道其大概宽度。老师和大家行动起来,在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.?此时如果测得BD=12米,DC=6米,EC=5米,求两岸间的大致距离AB.ADCEB相似三角形应用——测宽度思考:在这个方案中,需要测量哪些数据呢?例2:如图,在距离昭君墓186公里的鄂尔多斯响沙湾是国家5A级旅游景区。景区内有一条水流湍急的小河,有同学想要知道其大概宽度。老师和大家行动起来,在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.?此时如果测得BD=12米,DC=6米,EC=5米,求两岸间的大致距离AB.解: 因为 ∠ADB=∠EDC, ∠ABC=∠ECD=90°, ? 所以 △ABD∽△ECD, 答: 两岸间的大致距离为10米. ?(方法一)相似三角形应用——测宽度(方法二) 我们在河对岸选定一目标点A,在河的一边选点D和 E,使DE⊥AD,然后选点B,作BC∥DE,与视线EA相交于点C。AD EBC此时如果测得DE=12米,BC=8米,BD=5米,求两岸间的大致距离AB.思考:该方案中,需要量出哪些线段的长,才能测算出河宽?相似三角形应用——测宽度归纳:相似应用——测宽度测量不能直接到达的两点间的距离,通常也是构造相似三角形,利用相似三角形的性质求解。常用方法:(1)“A型”图,可测量出DE、BC、BD的长度,然后根据相似三角形的性质,求出AB的长度。
(2)“X”型图,可测量出BD、DC、EC的长度,然后根据相似三角形的性质,求出AB的长度。 通过本堂课的学习和探索,你学会了什么?
1.在实际生活中, 我们面对不能直接测量物体的高度和宽度时. 可以把它们转化为数学问题,建立相似三角形模型,再利用对应边的比相等来达到求解的目的!
2.能掌握并应用一些简单的相似三角形模型. 归纳:相似三角形的应用测量高度测量宽度1、在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?解:设高楼的高度为x米,由题意答:楼高36米.体验:相似应用——测高度所以 △ABC∽△DEF, 2.为了测量一池塘的宽AB,在岸边找到了一点C,使AC⊥AB,在AC上找到一点D,在BC上找到一点E,使DE⊥AC,测出AD=20m,DC=30m,DE =40m,那么你能算出池塘的宽AB吗?体验:相似应用——测宽度体验:相似应用——测宽度3.如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边15米的点处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为 米.某同学相测量旗杆的高度,在某一时刻他测得1米长的竹竿竖直时影长为1.5米。在同一时刻测量旗杆的影长时,因靠近一幢楼房,影子不能全落在地面上,有一部分落在墙上,他测得落在面上的影长为21米,留在墙上的影高为2米,你能帮助他测出旗杆的高度吗?拓展:相似三角形的应用ABCD某同学相测量旗杆的高度,在某一时刻他测得1米长的竹竿竖直时影长为1.5米。在同一时刻测量旗杆的影长时,因靠近一幢楼房,影子不能全落在地面上,有一部分落在墙上,他测得落在面上的影长为21米,留在墙上的影高为2米,你能帮助他测出旗杆的高度吗?拓展:相似三角形的应用ABCDE某同学相测量旗杆的高度,在某一时刻他测得1米长的竹竿竖直时影长为1.5米。在同一时刻测量旗杆的影长时,因靠近一幢楼房,影子不能全落在地面上,有一部分落在墙上,他测得落在面上的影长为21米,留在墙上的影高为2米,你能帮助他测出旗杆的高度吗?拓展:相似三角形的应用E如图,数学兴趣小组的同学们想利用树影测量树高。课外活动时,他们在阳光下测得一根长为1m的竹杆的影子是0.9m,但当他们测量树高时,发现树的影子不全落在地面上,有一部分影子落在数学楼的台阶上,且影子的末端刚好落在最后一级台阶的上端C处,他们认为继续测量也可以求出树高。随后测得落在地面的影长为1.1m,台阶总的高度为1.0m,水平总宽度为1.6m.请算一下树高是多少。(假设两次测量时太阳线是平行的)拓展:相似三角形的应用如图:小明想测量一颗大树AB的高度,发现树的影子恰好落在土坡的坡面CD和地面CB上,测得CD=4m,BC=10m,CD与地面成30度角,且测得1米竹杆的影子长为2米,那么树的高度是多少?C拓展:相似三角形的应用
相似三角形的应用举例读万卷书,行万里路1.定义: (对应角、对应边):三个角对应相等,三条边对应成比例的两个三角形相似。
2.预备定理(平行法):平行于三角形一边的直线与其他两边相交,所截得的三角形与原三角形相似。
3.判定定理一(边边边):三边成比例的两个三角形相似。
4.判定定理二(边角边):两边成比例且夹角相等的两个三角形相似。
5.判定定理三(角角):两角分别相等的两个三角形相似。
6.判定结论(HL):斜边与直角边成比例的两个直角三角形相似。一 、判断两三角形相似有哪些方法?二、相似三角形有什么性质?对应角相等,对应线段的比相等三、相似三角形可以解决哪些实际问题?相似三角形的应用昭君墓位于呼和浩特南郊9公里处的大黑河畔,是后人追慕和纪念王昭君的遗迹。坐落在呼市南郊的昭君墓,是塞外影响最大的一座昭君墓,整体占地面积近100亩,墓身呈台体状,墓顶建有一座凉亭,墓地东侧是历代名人为昭君墓题写的碑文,西侧是文物陈列室。 我们去旅行:内蒙昭君墓相似三角形应用——测高度在一个艳阳高照的上午,老师带领同学们来到昭君纪念陵,同学四处参观着。其间,有同学提出一个问题,这个昭君墓究竟有多高呢?这个问题引起了大家的兴趣。给你一条2米高的木杆,一把皮尺.你能利用所学知识来测出整个墓高吗?相似三角形应用——测高度我们去旅行:一个同学想出了一种测量昭君墓高度的方法:如图所示,为了测量昭君墓的高度OB,先竖一根已知长度的木棒O′B′,比较木棒的影长A′B′与昭君墓的影长AB,即可近似算出昭君墓的高度OB.相似三角形应用——测高度思考:昭君墓的影长AB怎么量?解: 由于太阳光是平行光线,因此∠OAB=∠O′A′B′. 又∠ABO=∠A′B′O′=90°.所以△OAB∽△O′A′B′,OB∶O′B′=AB∶A′B′,即昭君墓的高为33米.例1:如果O′B′=2,A′B′=4,AB=66,求昭君墓的高度OB.相似三角形应用——测高度相似三角形应用——测高度得到这个结果后,大家很开心,又有眼尖的同学看到昭君纪念堂前的广场上有一根旗杆,他们又想测量旗杆的高度。可在操作时,却发现旗杆的影子有一段落在了旁边的一个喷水池中,无法直接测量影长,怎么办呢?相似三角形应用——测高度当再次利用数学知识解决了生活中的难题后,有些同学已忘记参观了,他们对测物体高度产生浓厚兴趣,又有同学嚷起来,说要测广场边上的大树的高。老师趁热打铁,肯定了同学们的积极性,但同时又提出了新要求,不再提供标杆,要求大家动脑再想想有没有其他办法。归纳:相似应用——测高度利用相似三角形的性质解决实际测高问题的核心是构造相似三角形,在构造的三角形中被测物体必须是其中的一边。常用方法:(1)利用阳光下的影子(△ABC∽ △DEF) (2)利用标杆(△AEC∽ △AFM) (3)利用镜子的反射(△ABC∽ △DEC)
例2:如图,在距离昭君墓186公里的鄂尔多斯响沙湾是国家5A级旅游景区。景区内有一条水流湍急的小河,有同学想要知道其大概宽度。老师和大家行动起来,在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.?此时如果测得BD=12米,DC=6米,EC=5米,求两岸间的大致距离AB.ADCEB相似三角形应用——测宽度思考:在这个方案中,需要测量哪些数据呢?例2:如图,在距离昭君墓186公里的鄂尔多斯响沙湾是国家5A级旅游景区。景区内有一条水流湍急的小河,有同学想要知道其大概宽度。老师和大家行动起来,在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.?此时如果测得BD=12米,DC=6米,EC=5米,求两岸间的大致距离AB.解: 因为 ∠ADB=∠EDC, ∠ABC=∠ECD=90°, ? 所以 △ABD∽△ECD, 答: 两岸间的大致距离为10米. ?(方法一)相似三角形应用——测宽度(方法二) 我们在河对岸选定一目标点A,在河的一边选点D和 E,使DE⊥AD,然后选点B,作BC∥DE,与视线EA相交于点C。AD EBC此时如果测得DE=12米,BC=8米,BD=5米,求两岸间的大致距离AB.思考:该方案中,需要量出哪些线段的长,才能测算出河宽?相似三角形应用——测宽度归纳:相似应用——测宽度测量不能直接到达的两点间的距离,通常也是构造相似三角形,利用相似三角形的性质求解。常用方法:(1)“A型”图,可测量出DE、BC、BD的长度,然后根据相似三角形的性质,求出AB的长度。
(2)“X”型图,可测量出BD、DC、EC的长度,然后根据相似三角形的性质,求出AB的长度。 通过本堂课的学习和探索,你学会了什么?
1.在实际生活中, 我们面对不能直接测量物体的高度和宽度时. 可以把它们转化为数学问题,建立相似三角形模型,再利用对应边的比相等来达到求解的目的!
2.能掌握并应用一些简单的相似三角形模型. 归纳:相似三角形的应用测量高度测量宽度1、在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?解:设高楼的高度为x米,由题意答:楼高36米.体验:相似应用——测高度所以 △ABC∽△DEF, 2.为了测量一池塘的宽AB,在岸边找到了一点C,使AC⊥AB,在AC上找到一点D,在BC上找到一点E,使DE⊥AC,测出AD=20m,DC=30m,DE =40m,那么你能算出池塘的宽AB吗?体验:相似应用——测宽度体验:相似应用——测宽度3.如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边15米的点处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为 米.某同学相测量旗杆的高度,在某一时刻他测得1米长的竹竿竖直时影长为1.5米。在同一时刻测量旗杆的影长时,因靠近一幢楼房,影子不能全落在地面上,有一部分落在墙上,他测得落在面上的影长为21米,留在墙上的影高为2米,你能帮助他测出旗杆的高度吗?拓展:相似三角形的应用ABCD某同学相测量旗杆的高度,在某一时刻他测得1米长的竹竿竖直时影长为1.5米。在同一时刻测量旗杆的影长时,因靠近一幢楼房,影子不能全落在地面上,有一部分落在墙上,他测得落在面上的影长为21米,留在墙上的影高为2米,你能帮助他测出旗杆的高度吗?拓展:相似三角形的应用ABCDE某同学相测量旗杆的高度,在某一时刻他测得1米长的竹竿竖直时影长为1.5米。在同一时刻测量旗杆的影长时,因靠近一幢楼房,影子不能全落在地面上,有一部分落在墙上,他测得落在面上的影长为21米,留在墙上的影高为2米,你能帮助他测出旗杆的高度吗?拓展:相似三角形的应用E如图,数学兴趣小组的同学们想利用树影测量树高。课外活动时,他们在阳光下测得一根长为1m的竹杆的影子是0.9m,但当他们测量树高时,发现树的影子不全落在地面上,有一部分影子落在数学楼的台阶上,且影子的末端刚好落在最后一级台阶的上端C处,他们认为继续测量也可以求出树高。随后测得落在地面的影长为1.1m,台阶总的高度为1.0m,水平总宽度为1.6m.请算一下树高是多少。(假设两次测量时太阳线是平行的)拓展:相似三角形的应用如图:小明想测量一颗大树AB的高度,发现树的影子恰好落在土坡的坡面CD和地面CB上,测得CD=4m,BC=10m,CD与地面成30度角,且测得1米竹杆的影子长为2米,那么树的高度是多少?C拓展:相似三角形的应用
