3.1回归分析初步应用(1)07.11.12(浙江省嘉兴市桐乡市)
文档属性
| 名称 | 3.1回归分析初步应用(1)07.11.12(浙江省嘉兴市桐乡市) |  | |
| 格式 | rar | ||
| 文件大小 | 103.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-14 14:11:00 | ||
图片预览






文档简介
课件30张PPT。第一章 统计案例1.1回归分析的基本思想及其初步应用(第二课时)a. 比《数学3》中“回归”增加的内容数学3——统计
画散点图
了解最小二乘法的思想
求回归直线方程
y=bx+a
用回归直线方程解决应用问题选修1-2——统计案例
引入线性回归模型
y=bx+a+e
了解模型中随机误差项e产生的原因
了解相关指数 R2 和模型拟合的效果之间的关系
了解残差图的作用
利用线性回归模型解决一类非线性回归问题
正确理解分析方法与结果什么是回归分析:“回归”一词是由英国生物学家F.Galton在研究人体身高的遗传问题时首先提出的。 根据遗传学的观点,子辈的身高受父辈影响,以X记父辈身高,Y记子辈身高。
虽然子辈身高一般受父辈影响,但同样身高的父亲,其子身高并不一致,因此,
X和Y之间存在一种相关关系。 一般而言,父辈身高者,其子辈身高也高,依此推论,祖祖辈辈遗传下来,身
高必然向两极分化,而事实上并非如此,显然有一种力量将身高拉向中心,即子辈
的身高有向中心回归的特点。“回归”一词即源于此。 虽然这种向中心回归的现象只是特定领域里的结论,并不具有普遍性,但从它
所描述的关于X为自变量,Y为不确定的因变量这种变量间的关系看,和我们现在的
回归含义是相同的。 不过,现代回归分析虽然沿用了“回归”一词,但内容已有很大变化,它是一种应用
于许多领域的广泛的分析研究方法,在经济理论研究和实证研究中也发挥着重要作用。回归分析的内容与步骤:
统计检验通过后,最后是利用回归模型,根据自变量去估计、预测因变量。 回归分析通过一个变量或一些变量的变化解释另一变量的变化。 其主要内容和步骤是,
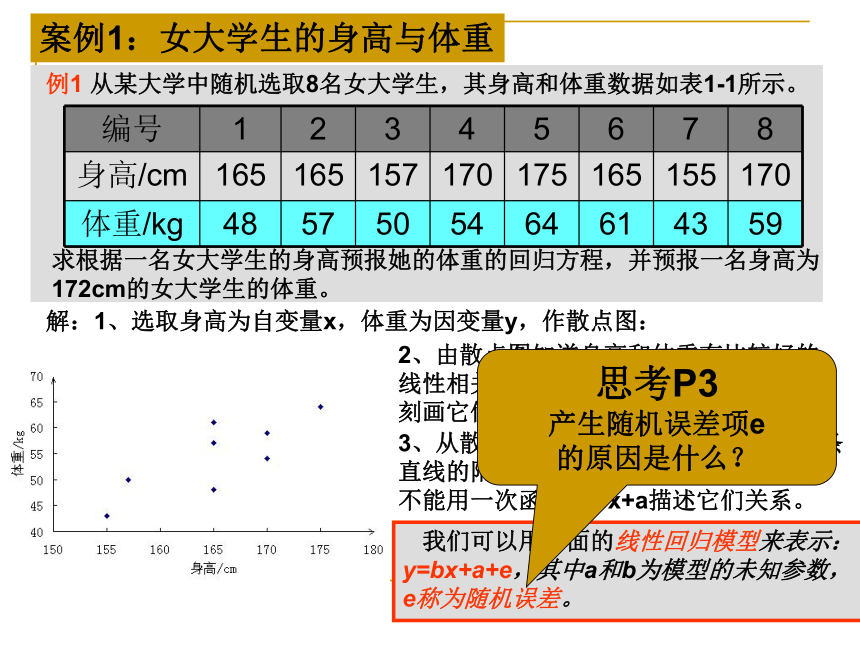
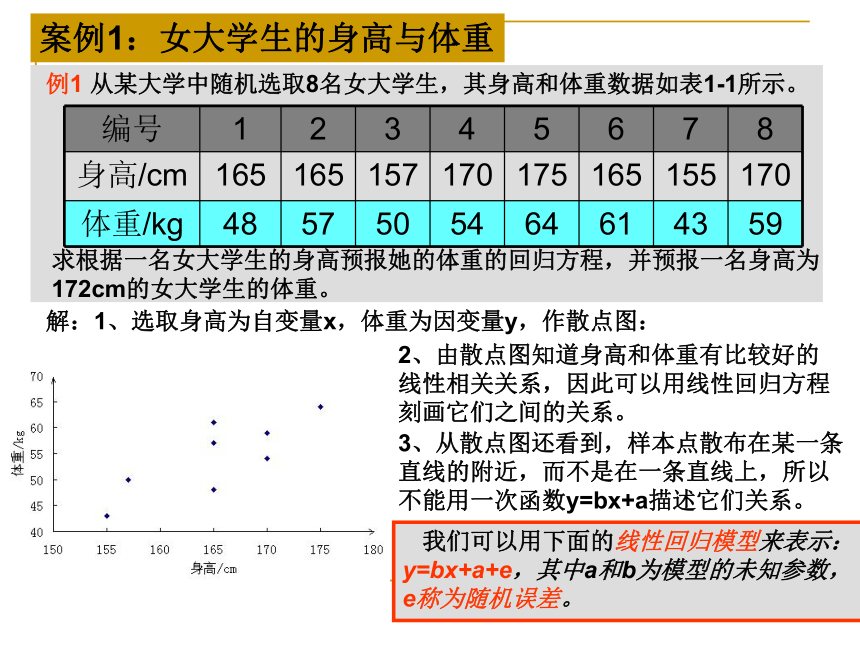
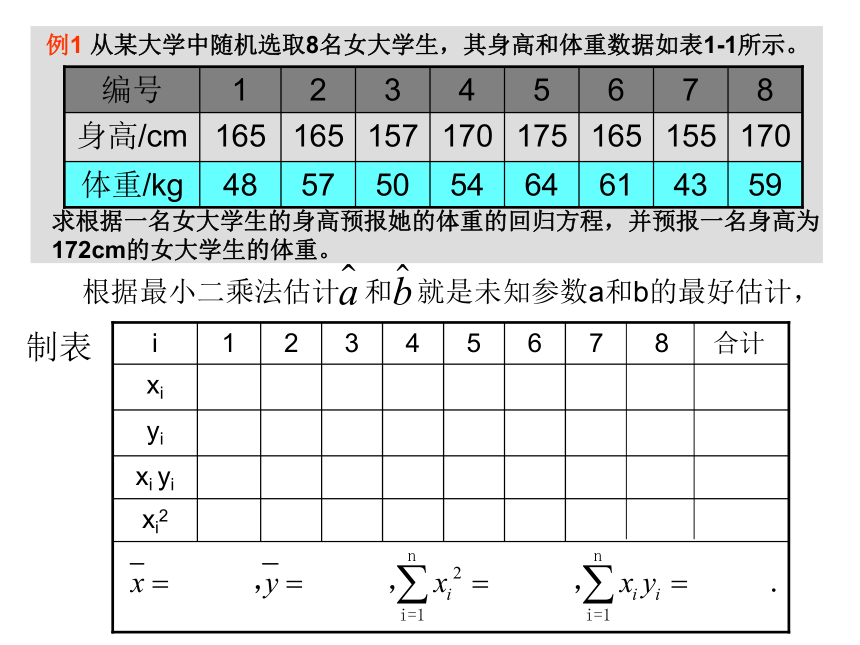
首先根据理论和对问题的分析判断,将变量分为自变量和因变量;其次,设法找出合适的数学方程式(即回归模型)描述变量间的关系;由于涉及到的变量具有不确定性,接着还要对回归模型进行统计检验;例1 从某大学中随机选取8名女大学生,其身高和体重数据如表1-1所示。求根据一名女大学生的身高预报她的体重的回归方程,并预报一名身高为
172cm的女大学生的体重。案例1:女大学生的身高与体重解:1、选取身高为自变量x,体重为因变量y,作散点图:2、由散点图知道身高和体重有比较好的
线性相关关系,因此可以用线性回归方程
刻画它们之间的关系。3、从散点图还看到,样本点散布在某一条
直线的附近,而不是在一条直线上,所以
不能用一次函数y=bx+a描述它们关系。 我们可以用下面的线性回归模型来表示:
y=bx+a+e,其中a和b为模型的未知参数,
e称为随机误差。思考P3
产生随机误差项e
的原因是什么?思考P3
产生随机误差项e的原因是什么?随机误差e的来源(可以推广到一般):
1、其它因素的影响:影响身高 y 的因素不只是体重 x,可能 还包括遗传基因、饮食习惯、生长环境等因素;
2、用线性回归模型近似真实模型所引起的误差;
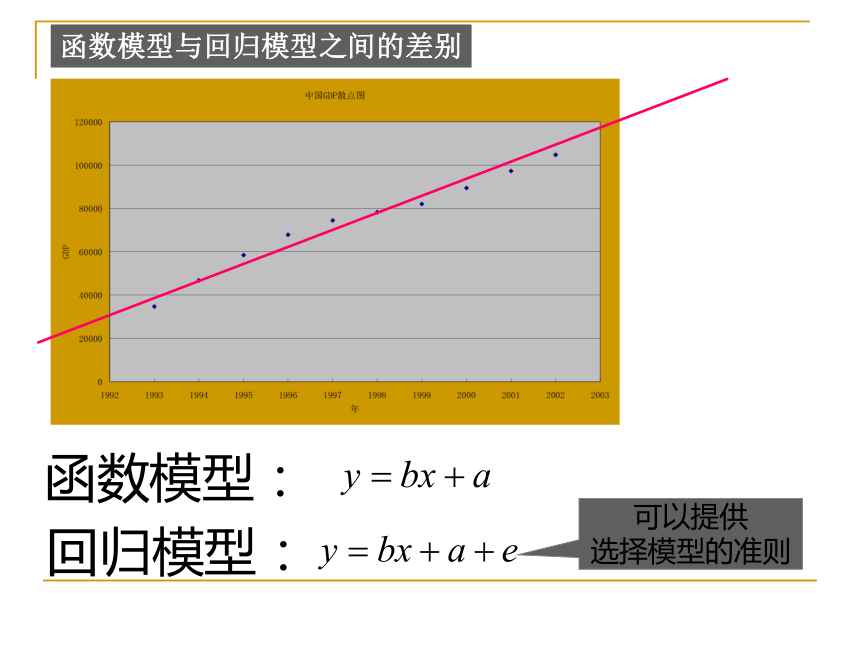
3、身高 y 的观测误差。函数模型与回归模型之间的差别函数模型:回归模型:可以提供
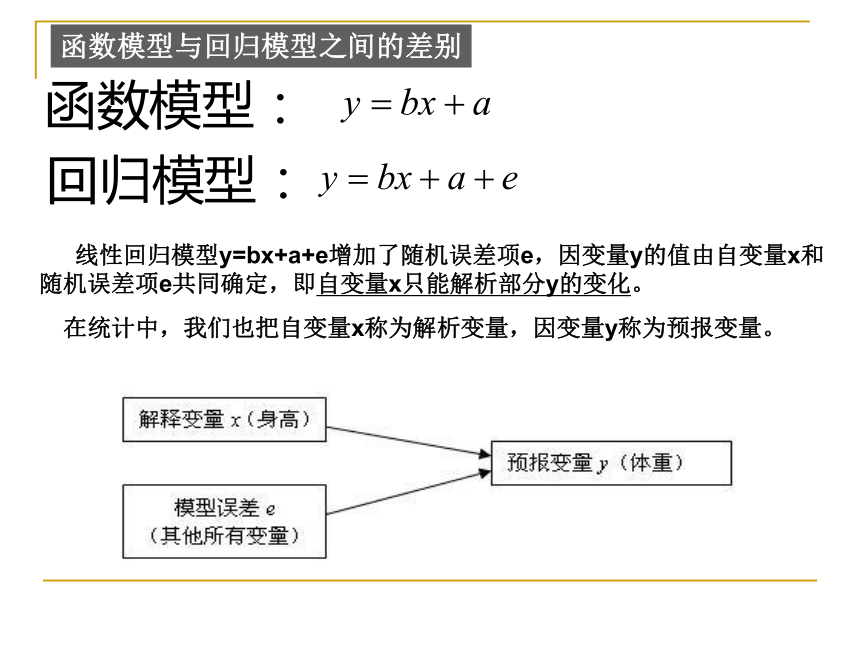
选择模型的准则函数模型与回归模型之间的差别函数模型:回归模型: 线性回归模型y=bx+a+e增加了随机误差项e,因变量y的值由自变量x和
随机误差项e共同确定,即自变量x只能解析部分y的变化。 在统计中,我们也把自变量x称为解析变量,因变量y称为预报变量。例1 从某大学中随机选取8名女大学生,其身高和体重数据如表1-1所示。求根据一名女大学生的身高预报她的体重的回归方程,并预报一名身高为
172cm的女大学生的体重。案例1:女大学生的身高与体重解:1、选取身高为自变量x,体重为因变量y,作散点图:2、由散点图知道身高和体重有比较好的
线性相关关系,因此可以用线性回归方程
刻画它们之间的关系。3、从散点图还看到,样本点散布在某一条
直线的附近,而不是在一条直线上,所以
不能用一次函数y=bx+a描述它们关系。 我们可以用下面的线性回归模型来表示:
y=bx+a+e,其中a和b为模型的未知参数,
e称为随机误差。根据最小二乘法估计 和 就是未知参数a和b的最好估计,根据最小二乘法估计 和 就是未知参数a和b的最好估计,于是有b=所以回归方程是所以,对于身高为172cm的女大学生,由回归方程可以预报其体重为
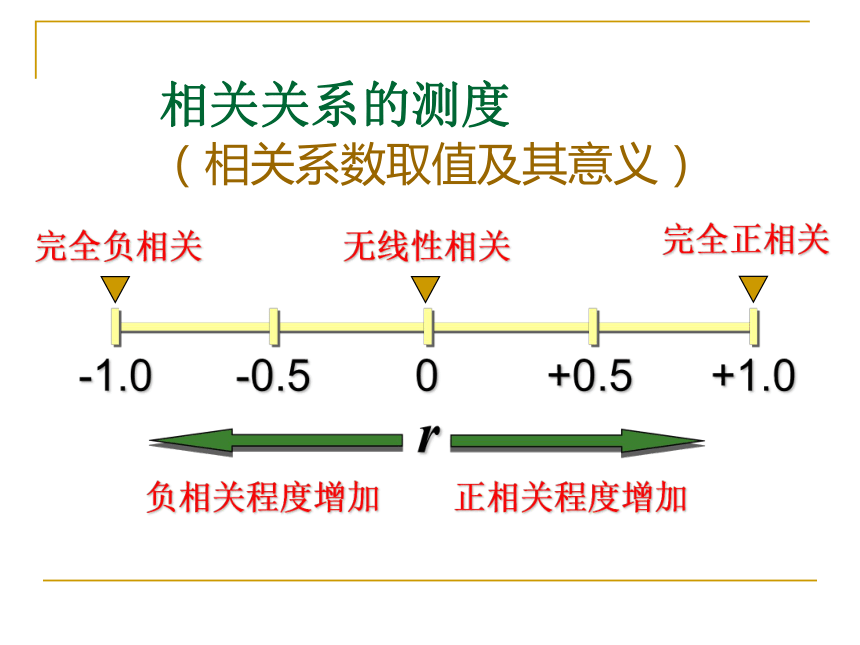
相关关系的测度 (相关系数取值及其意义)r对回归模型进行统计检验思考P6:
如何刻画预报变量(体重)的变化?这个变化在多大程度上
与解析变量(身高)有关?在多大程度上与随机误差有关? 假设身高和随机误差的不同不会对体重产生任何影响,那么所有人的体重将相
同。在体重不受任何变量影响的假设下,设8名女大学生的体重都是她们的平均值,
即8个人的体重都为54.5kg。在散点图中,所有的点应该落在同一条
水平直线上,但是观测到的数据并非如
此。这就意味着预报变量(体重)的值
受解析变量(身高)或随机误差的影响。 例如,编号为6的女大学生的体重并没有落在水平直线上,她的体重为61kg。解析
变量(身高)和随机误差共同把这名学生的体重从54.5kg“推”到了61kg,相差6.5kg,
所以6.5kg是解析变量和随机误差的组合效应。 编号为3的女大学生的体重并也没有落在水平直线上,她的体重为50kg。解析
变量(身高)和随机误差共同把这名学生的体重从54.5kg“推”到了50kg,相差-4.5kg,
这时解析变量和随机误差的组合效应为-4.5kg。用这种方法可以对所有预报变量计算组合效应。在例1中,总偏差平方和为354。 那么,在这个总的效应(总偏差平方和)中,有多少来自于解析变量(身高)?
有多少来自于随机误差? 假设随机误差对体重没有影响,也就是说,体重仅受身高的影响,那么散点图
中所有的点将完全落在回归直线上。但是,在图中,数据点并没有完全落在回归
直线上。这些点散布在回归直线附近,所以一定是随机误差把这些点从回归直线上
“推”开了。在例1中,残差平方和约为128.361。例如,编号为6的女大学生,计算随机误差的效应(残差)为: 由于解析变量和随机误差的总效应(总偏差平方和)为354,而随机误差的效应为
128.361,所以解析变量的效应为解析变量和随机误差的总效应(总偏差平方和)
=解析变量的效应(回归平方和)+随机误差的效应(残差平方和)离差平方和的分解 (三个平方和的意义)总偏差平方和(SST)
反映因变量的 n 个观察值与其均值的总离差
回归平方和(SSR)
反映自变量 x 的变化对因变量 y 取值变化的影响,或者说,是由于 x 与 y 之间的线性关系引起的 y 的取值变化,也称为可解释的平方和
残差平方和(SSE)
反映除 x 以外的其他因素对 y 取值的影响,也称为不可解释的平方和或剩余平方和样本决定系数 (判定系数 r2 )回归平方和占总离差平方和的比例
反映回归直线的拟合程度
取值范围在 [ 0 , 1 ] 之间
r2 ?1,说明回归方程拟合的越好;r2?0,说明回归方程拟合的越差
判定系数等于相关系数的平方,即r2=(r)2显然,R2的值越大,说明残差平方和越小,也就是说模型拟合效果越好。在线性回归模型中,R2表示解析变量对预报变量变化的贡献率。 R2越接近1,表示回归的效果越好(因为R2越接近1,表示解析变量和预报变量的
线性相关性越强)。 如果某组数据可能采取几种不同回归方程进行回归分析,则可以通过比较R2的值
来做出选择,即选取R2较大的模型作为这组数据的模型。总的来说:
相关指数R2是度量模型拟合效果的一种指标。
在线性模型中,它代表自变量刻画预报变量的能力。 从表3-1中可以看出,解析变量对总效应约贡献了64%,即R2 0.64,可以叙述为
“身高解析了64%的体重变化”,而随机误差贡献了剩余的36%。
所以,身高对体重的效应比随机误差的效应大得多。表1-4列出了女大学生身高和体重的原始数据以及相应的残差数据。 在研究两个变量间的关系时,首先要根据散点图来粗略判断它们是否线性相关,
是否可以用回归模型来拟合数据。残差分析与残差图的定义: 然后,我们可以通过残差 来判断模型拟合的效果,判断原始
数据中是否存在可疑数据,这方面的分析工作称为残差分析。 我们可以利用图形来分析残差特性,作图时纵坐标为残差,横坐标可以选为样本
编号,或身高数据,或体重估计值等,这样作出的图形称为残差图。残差图的制作及作用。
坐标纵轴为残差变量,横轴可以有不同的选择;
若模型选择的正确,残差图中的点应该分布在以横轴为心的带形区域;
对于远离横轴的点,要特别注意。身高与体重残差图 几点说明:
第一个样本点和第6个样本点的残差比较大,需要确认在采集过程中是否有人为的错误。如果数据采集有错误,就予以纠正,然后再重新利用线性回归模型拟合数据;如果数据采集没有错误,则需要寻找其他的原因。
另外,残差点比较均匀地落在水平的带状区域中,说明选用的模型计较合适,这样的带状区域的宽度越窄,说明模型拟合精度越高,回归方程的预报精度越高。小结——这些问题也使用于其他问题。涉及到统计的一些思想:
模型适用的总体;
模型的时间性;
样本的取值范围对模型的影响;
模型预报结果的正确理解。一般地,建立回归模型的基本步骤为:(1)确定研究对象,明确哪个变量是解析变量,哪个变量是预报变量。(2)画出确定好的解析变量和预报变量的散点图,观察它们之间的关系
(如是否存在线性关系等)。(3)由经验确定回归方程的类型(如我们观察到数据呈线性关系,则选用线性
回归方程y=bx+a).(4)按一定规则估计回归方程中的参数(如最小二乘法)。(5)得出结果后分析残差图是否有异常(个别数据对应残差过大,或残差呈现
不随机的规律性,等等),过存在异常,则检查数据是否有误,或模型是
否合适等。什么是回归分析? (内容)从一组样本数据出发,确定变量之间的数学关系式
对这些关系式的可信程度进行各种统计检验,并从影响某一特定变量的诸多变量中找出哪些变量的影响显著,哪些不显著
利用所求的关系式,根据一个或几个变量的取值来预测或控制另一个特定变量的取值,并给出这种预测或控制的精确程度结束回归分析与相关分析的区别相关分析中,变量 x 变量 y 处于平等的地位;回归分析中,变量 y 称为因变量,处在被解释的地位,x 称为自变量,用于预测因变量的变化
相关分析中所涉及的变量 x 和 y 都是随机变量;回归分析中,因变量 y 是随机变量,自变量 x 可以是随机变量,也可以是非随机的确定变量
相关分析主要是描述两个变量之间线性关系的密切程度;回归分析不仅可以揭示变量 x 对变量 y 的影响大小,还可以由回归方程进行预测和控制
画散点图
了解最小二乘法的思想
求回归直线方程
y=bx+a
用回归直线方程解决应用问题选修1-2——统计案例
引入线性回归模型
y=bx+a+e
了解模型中随机误差项e产生的原因
了解相关指数 R2 和模型拟合的效果之间的关系
了解残差图的作用
利用线性回归模型解决一类非线性回归问题
正确理解分析方法与结果什么是回归分析:“回归”一词是由英国生物学家F.Galton在研究人体身高的遗传问题时首先提出的。 根据遗传学的观点,子辈的身高受父辈影响,以X记父辈身高,Y记子辈身高。
虽然子辈身高一般受父辈影响,但同样身高的父亲,其子身高并不一致,因此,
X和Y之间存在一种相关关系。 一般而言,父辈身高者,其子辈身高也高,依此推论,祖祖辈辈遗传下来,身
高必然向两极分化,而事实上并非如此,显然有一种力量将身高拉向中心,即子辈
的身高有向中心回归的特点。“回归”一词即源于此。 虽然这种向中心回归的现象只是特定领域里的结论,并不具有普遍性,但从它
所描述的关于X为自变量,Y为不确定的因变量这种变量间的关系看,和我们现在的
回归含义是相同的。 不过,现代回归分析虽然沿用了“回归”一词,但内容已有很大变化,它是一种应用
于许多领域的广泛的分析研究方法,在经济理论研究和实证研究中也发挥着重要作用。回归分析的内容与步骤:
统计检验通过后,最后是利用回归模型,根据自变量去估计、预测因变量。 回归分析通过一个变量或一些变量的变化解释另一变量的变化。 其主要内容和步骤是,
首先根据理论和对问题的分析判断,将变量分为自变量和因变量;其次,设法找出合适的数学方程式(即回归模型)描述变量间的关系;由于涉及到的变量具有不确定性,接着还要对回归模型进行统计检验;例1 从某大学中随机选取8名女大学生,其身高和体重数据如表1-1所示。求根据一名女大学生的身高预报她的体重的回归方程,并预报一名身高为
172cm的女大学生的体重。案例1:女大学生的身高与体重解:1、选取身高为自变量x,体重为因变量y,作散点图:2、由散点图知道身高和体重有比较好的
线性相关关系,因此可以用线性回归方程
刻画它们之间的关系。3、从散点图还看到,样本点散布在某一条
直线的附近,而不是在一条直线上,所以
不能用一次函数y=bx+a描述它们关系。 我们可以用下面的线性回归模型来表示:
y=bx+a+e,其中a和b为模型的未知参数,
e称为随机误差。思考P3
产生随机误差项e
的原因是什么?思考P3
产生随机误差项e的原因是什么?随机误差e的来源(可以推广到一般):
1、其它因素的影响:影响身高 y 的因素不只是体重 x,可能 还包括遗传基因、饮食习惯、生长环境等因素;
2、用线性回归模型近似真实模型所引起的误差;
3、身高 y 的观测误差。函数模型与回归模型之间的差别函数模型:回归模型:可以提供
选择模型的准则函数模型与回归模型之间的差别函数模型:回归模型: 线性回归模型y=bx+a+e增加了随机误差项e,因变量y的值由自变量x和
随机误差项e共同确定,即自变量x只能解析部分y的变化。 在统计中,我们也把自变量x称为解析变量,因变量y称为预报变量。例1 从某大学中随机选取8名女大学生,其身高和体重数据如表1-1所示。求根据一名女大学生的身高预报她的体重的回归方程,并预报一名身高为
172cm的女大学生的体重。案例1:女大学生的身高与体重解:1、选取身高为自变量x,体重为因变量y,作散点图:2、由散点图知道身高和体重有比较好的
线性相关关系,因此可以用线性回归方程
刻画它们之间的关系。3、从散点图还看到,样本点散布在某一条
直线的附近,而不是在一条直线上,所以
不能用一次函数y=bx+a描述它们关系。 我们可以用下面的线性回归模型来表示:
y=bx+a+e,其中a和b为模型的未知参数,
e称为随机误差。根据最小二乘法估计 和 就是未知参数a和b的最好估计,根据最小二乘法估计 和 就是未知参数a和b的最好估计,于是有b=所以回归方程是所以,对于身高为172cm的女大学生,由回归方程可以预报其体重为
相关关系的测度 (相关系数取值及其意义)r对回归模型进行统计检验思考P6:
如何刻画预报变量(体重)的变化?这个变化在多大程度上
与解析变量(身高)有关?在多大程度上与随机误差有关? 假设身高和随机误差的不同不会对体重产生任何影响,那么所有人的体重将相
同。在体重不受任何变量影响的假设下,设8名女大学生的体重都是她们的平均值,
即8个人的体重都为54.5kg。在散点图中,所有的点应该落在同一条
水平直线上,但是观测到的数据并非如
此。这就意味着预报变量(体重)的值
受解析变量(身高)或随机误差的影响。 例如,编号为6的女大学生的体重并没有落在水平直线上,她的体重为61kg。解析
变量(身高)和随机误差共同把这名学生的体重从54.5kg“推”到了61kg,相差6.5kg,
所以6.5kg是解析变量和随机误差的组合效应。 编号为3的女大学生的体重并也没有落在水平直线上,她的体重为50kg。解析
变量(身高)和随机误差共同把这名学生的体重从54.5kg“推”到了50kg,相差-4.5kg,
这时解析变量和随机误差的组合效应为-4.5kg。用这种方法可以对所有预报变量计算组合效应。在例1中,总偏差平方和为354。 那么,在这个总的效应(总偏差平方和)中,有多少来自于解析变量(身高)?
有多少来自于随机误差? 假设随机误差对体重没有影响,也就是说,体重仅受身高的影响,那么散点图
中所有的点将完全落在回归直线上。但是,在图中,数据点并没有完全落在回归
直线上。这些点散布在回归直线附近,所以一定是随机误差把这些点从回归直线上
“推”开了。在例1中,残差平方和约为128.361。例如,编号为6的女大学生,计算随机误差的效应(残差)为: 由于解析变量和随机误差的总效应(总偏差平方和)为354,而随机误差的效应为
128.361,所以解析变量的效应为解析变量和随机误差的总效应(总偏差平方和)
=解析变量的效应(回归平方和)+随机误差的效应(残差平方和)离差平方和的分解 (三个平方和的意义)总偏差平方和(SST)
反映因变量的 n 个观察值与其均值的总离差
回归平方和(SSR)
反映自变量 x 的变化对因变量 y 取值变化的影响,或者说,是由于 x 与 y 之间的线性关系引起的 y 的取值变化,也称为可解释的平方和
残差平方和(SSE)
反映除 x 以外的其他因素对 y 取值的影响,也称为不可解释的平方和或剩余平方和样本决定系数 (判定系数 r2 )回归平方和占总离差平方和的比例
反映回归直线的拟合程度
取值范围在 [ 0 , 1 ] 之间
r2 ?1,说明回归方程拟合的越好;r2?0,说明回归方程拟合的越差
判定系数等于相关系数的平方,即r2=(r)2显然,R2的值越大,说明残差平方和越小,也就是说模型拟合效果越好。在线性回归模型中,R2表示解析变量对预报变量变化的贡献率。 R2越接近1,表示回归的效果越好(因为R2越接近1,表示解析变量和预报变量的
线性相关性越强)。 如果某组数据可能采取几种不同回归方程进行回归分析,则可以通过比较R2的值
来做出选择,即选取R2较大的模型作为这组数据的模型。总的来说:
相关指数R2是度量模型拟合效果的一种指标。
在线性模型中,它代表自变量刻画预报变量的能力。 从表3-1中可以看出,解析变量对总效应约贡献了64%,即R2 0.64,可以叙述为
“身高解析了64%的体重变化”,而随机误差贡献了剩余的36%。
所以,身高对体重的效应比随机误差的效应大得多。表1-4列出了女大学生身高和体重的原始数据以及相应的残差数据。 在研究两个变量间的关系时,首先要根据散点图来粗略判断它们是否线性相关,
是否可以用回归模型来拟合数据。残差分析与残差图的定义: 然后,我们可以通过残差 来判断模型拟合的效果,判断原始
数据中是否存在可疑数据,这方面的分析工作称为残差分析。 我们可以利用图形来分析残差特性,作图时纵坐标为残差,横坐标可以选为样本
编号,或身高数据,或体重估计值等,这样作出的图形称为残差图。残差图的制作及作用。
坐标纵轴为残差变量,横轴可以有不同的选择;
若模型选择的正确,残差图中的点应该分布在以横轴为心的带形区域;
对于远离横轴的点,要特别注意。身高与体重残差图 几点说明:
第一个样本点和第6个样本点的残差比较大,需要确认在采集过程中是否有人为的错误。如果数据采集有错误,就予以纠正,然后再重新利用线性回归模型拟合数据;如果数据采集没有错误,则需要寻找其他的原因。
另外,残差点比较均匀地落在水平的带状区域中,说明选用的模型计较合适,这样的带状区域的宽度越窄,说明模型拟合精度越高,回归方程的预报精度越高。小结——这些问题也使用于其他问题。涉及到统计的一些思想:
模型适用的总体;
模型的时间性;
样本的取值范围对模型的影响;
模型预报结果的正确理解。一般地,建立回归模型的基本步骤为:(1)确定研究对象,明确哪个变量是解析变量,哪个变量是预报变量。(2)画出确定好的解析变量和预报变量的散点图,观察它们之间的关系
(如是否存在线性关系等)。(3)由经验确定回归方程的类型(如我们观察到数据呈线性关系,则选用线性
回归方程y=bx+a).(4)按一定规则估计回归方程中的参数(如最小二乘法)。(5)得出结果后分析残差图是否有异常(个别数据对应残差过大,或残差呈现
不随机的规律性,等等),过存在异常,则检查数据是否有误,或模型是
否合适等。什么是回归分析? (内容)从一组样本数据出发,确定变量之间的数学关系式
对这些关系式的可信程度进行各种统计检验,并从影响某一特定变量的诸多变量中找出哪些变量的影响显著,哪些不显著
利用所求的关系式,根据一个或几个变量的取值来预测或控制另一个特定变量的取值,并给出这种预测或控制的精确程度结束回归分析与相关分析的区别相关分析中,变量 x 变量 y 处于平等的地位;回归分析中,变量 y 称为因变量,处在被解释的地位,x 称为自变量,用于预测因变量的变化
相关分析中所涉及的变量 x 和 y 都是随机变量;回归分析中,因变量 y 是随机变量,自变量 x 可以是随机变量,也可以是非随机的确定变量
相关分析主要是描述两个变量之间线性关系的密切程度;回归分析不仅可以揭示变量 x 对变量 y 的影响大小,还可以由回归方程进行预测和控制
