沪科版数学七年级下册 专题(十六)利用平移的性质计算 讲义
文档属性
| 名称 | 沪科版数学七年级下册 专题(十六)利用平移的性质计算 讲义 | 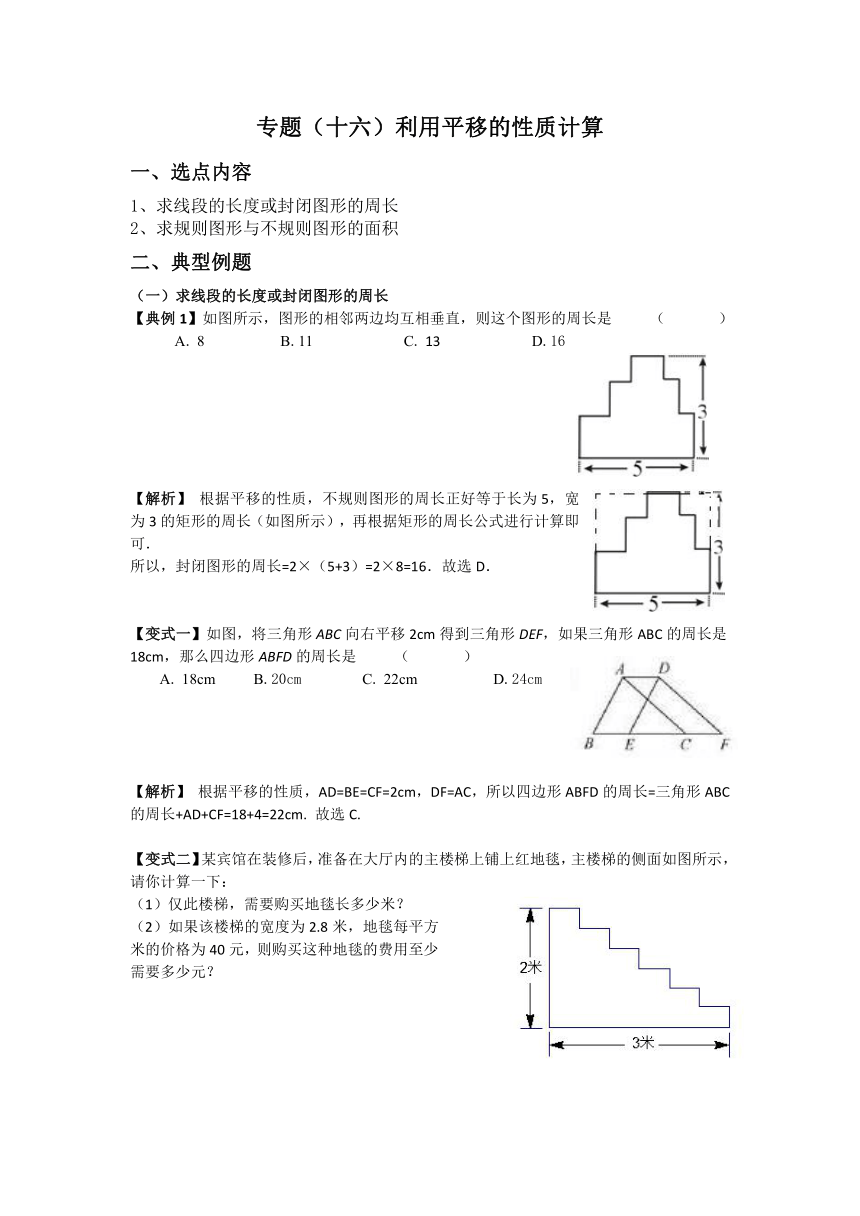 | |
| 格式 | docx | ||
| 文件大小 | 149.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 15:49:29 | ||
图片预览


文档简介
专题(十六)利用平移的性质计算
选点内容
1、求线段的长度或封闭图形的周长
2、求规则图形与不规则图形的面积
典型例题
求线段的长度或封闭图形的周长
【典例1】如图所示,图形的相邻两边均互相垂直,则这个图形的周长是 ( )
A. 8 B.11 C. 13 D.16
【解析】 根据平移的性质,不规则图形的周长正好等于长为5,宽为3的矩形的周长(如图所示),再根据矩形的周长公式进行计算即可.
所以,封闭图形的周长=2×(5+3)=2×8=16.故选D.
【变式一】如图,将三角形ABC向右平移2cm得到三角形DEF,如果三角形ABC的周长是18cm,那么四边形ABFD的周长是 ( )
A. 18cm B.20cm C. 22cm D.24cm
【解析】 根据平移的性质,AD=BE=CF=2cm,DF=AC,所以四边形ABFD的周长=三角形ABC的周长+AD+CF=18+4=22cm. 故选C.
【变式二】某宾馆在装修后,准备在大厅内的主楼梯上铺上红地毯,主楼梯的侧面如图所示,请你计算一下:
仅此楼梯,需要购买地毯长多少米?
如果该楼梯的宽度为2.8米,地毯每平方米的价格为40元,则购买这种地毯的费用至少需要多少元?
【解析】(1) 根据平移的性质,此楼梯水平方向的长度之和等于3米,竖直方向的长度之和等于2米,所以需要购买地毯的长度为5米.
(2)
答:购买这种地毯的费用至少需要560元.
【重难点剖析】 解决此类问题,重点在于利用平移变换的性质,难点在于通过平移,把不规则图形的周长转化为规则图形的周长,或者通过平移,达到化零为整的目的进行求解.
求规则图形与不规则图形的面积
【典例2】 如图,将直角三角形ABC沿BC方向平移得到三角形DEF的位置.若AB=8cm,BE=4cm,DG=3cm,则图中阴影部分的面积为_____cm.
【解析】虽然阴影部分是一个梯形,但因其上底CG、下底DF和高都不易求出,故直接用梯形的面积公式去求它的面积很困难;由于不知道CE的长,又无法通过S阴影部分=S三角形DEF-SSJX GEC来求解.由题意,知三角形DEF是三角形ABC沿BC方向平移得到的,所以阴影部分的面积等于梯形ABEG的面积,从而S阴影部分=(AB+GE)BE=[8+(8-3)]×4=26 cm2.
【变式一】如图所示是某小区一块空地,规划人员把它分割成①号区(空白部分)、②号区(阴影部分)、③号区(图下方的空白部分)三块,拟在①号区种花、②号区建一个露天活动场所、③号区植树,已知图中四边形ABCD与四边形EFGH是两个完全相同的直角梯形(一腰和底相交成直角的梯形叫做直角梯形,这里∠C和∠G都是直角),点A、E、B、F在一条直线上,求①号区种花部分的面积.
【解析】显然,因①号区是不规则的图形,不易直接求其面积,考虑到四边形ABCD与四边形EFGH是两个完全相同的直角梯形,故可将四边形EFGH看成是四边形ABCD沿AB方向平移得到的,所以①号区面积等于③号区面积,而③号区面积等于×(EM+AD)×MD=×(80-1+80)×2=159(m2),所以种花部分的面积为159(m2).
【重难点剖析】 此类题主要考查了平移的性质——平移后的图形与原图形大小、形状都不变,面积自然也不变.因此,在变式题中,①号区面积+②号区面积=②号区面积+③号区面积,所以①号区面积=③号区面积.这类题的特点往往是声东击西,所以解题的对策就是转移目标.
【典例3】现一块白色正方形手帕,它的边长是18cm,上面横、竖各有两道红条,如图所示,红条的宽是2cm,怎样利用平移的知识,求出白色部分的面积?
【解析】将黑条平移到边缘,则白色部分的边长为18-2×2=14,
白色部分的面积为14×14=196(cm2).
【变式一】如图,由两个大小相同的正方形拼成一个长方形,正方形的边长是5,图中的阴影部分是有半径为5的圆弧和正方形的边围成的,求阴影部分的面积.
【解析】 由图形可知,将右边正方形中的阴影部分向左平移5个单位,正好与左边正方形中空白部分重合,所以图中阴影部分的面积恰好等于一个正方形的面积,故阴影部分的面积=5×5=25(平方单位).
【变式二】如图,在长为50m,宽为22m的长方形地面上修筑宽度都为2m的道路,余下的部分种植花草,求种植花草部分的面积.
【解析】如图,将几条2米宽的 小路分别平移到大长方形的上边缘和左边缘,则种植花草部分汇集成一个长方形,显然,这个长方形的长为48米,宽为20 米,所以,种植花草部分的面积为48×20=960平方米。
【重难点剖析】 此类题主要考查了图形的平移及平移的性质,关键是如何将不规则图形化为规则图形,或者将分散的部分化成一个整体,具体的做法是,把一个图形的整体或部分沿某一直线方向移动,得到一个新的图形,要求新图形与原图形的面积大小完全相同.
选点内容
1、求线段的长度或封闭图形的周长
2、求规则图形与不规则图形的面积
典型例题
求线段的长度或封闭图形的周长
【典例1】如图所示,图形的相邻两边均互相垂直,则这个图形的周长是 ( )
A. 8 B.11 C. 13 D.16
【解析】 根据平移的性质,不规则图形的周长正好等于长为5,宽为3的矩形的周长(如图所示),再根据矩形的周长公式进行计算即可.
所以,封闭图形的周长=2×(5+3)=2×8=16.故选D.
【变式一】如图,将三角形ABC向右平移2cm得到三角形DEF,如果三角形ABC的周长是18cm,那么四边形ABFD的周长是 ( )
A. 18cm B.20cm C. 22cm D.24cm
【解析】 根据平移的性质,AD=BE=CF=2cm,DF=AC,所以四边形ABFD的周长=三角形ABC的周长+AD+CF=18+4=22cm. 故选C.
【变式二】某宾馆在装修后,准备在大厅内的主楼梯上铺上红地毯,主楼梯的侧面如图所示,请你计算一下:
仅此楼梯,需要购买地毯长多少米?
如果该楼梯的宽度为2.8米,地毯每平方米的价格为40元,则购买这种地毯的费用至少需要多少元?
【解析】(1) 根据平移的性质,此楼梯水平方向的长度之和等于3米,竖直方向的长度之和等于2米,所以需要购买地毯的长度为5米.
(2)
答:购买这种地毯的费用至少需要560元.
【重难点剖析】 解决此类问题,重点在于利用平移变换的性质,难点在于通过平移,把不规则图形的周长转化为规则图形的周长,或者通过平移,达到化零为整的目的进行求解.
求规则图形与不规则图形的面积
【典例2】 如图,将直角三角形ABC沿BC方向平移得到三角形DEF的位置.若AB=8cm,BE=4cm,DG=3cm,则图中阴影部分的面积为_____cm.
【解析】虽然阴影部分是一个梯形,但因其上底CG、下底DF和高都不易求出,故直接用梯形的面积公式去求它的面积很困难;由于不知道CE的长,又无法通过S阴影部分=S三角形DEF-SSJX GEC来求解.由题意,知三角形DEF是三角形ABC沿BC方向平移得到的,所以阴影部分的面积等于梯形ABEG的面积,从而S阴影部分=(AB+GE)BE=[8+(8-3)]×4=26 cm2.
【变式一】如图所示是某小区一块空地,规划人员把它分割成①号区(空白部分)、②号区(阴影部分)、③号区(图下方的空白部分)三块,拟在①号区种花、②号区建一个露天活动场所、③号区植树,已知图中四边形ABCD与四边形EFGH是两个完全相同的直角梯形(一腰和底相交成直角的梯形叫做直角梯形,这里∠C和∠G都是直角),点A、E、B、F在一条直线上,求①号区种花部分的面积.
【解析】显然,因①号区是不规则的图形,不易直接求其面积,考虑到四边形ABCD与四边形EFGH是两个完全相同的直角梯形,故可将四边形EFGH看成是四边形ABCD沿AB方向平移得到的,所以①号区面积等于③号区面积,而③号区面积等于×(EM+AD)×MD=×(80-1+80)×2=159(m2),所以种花部分的面积为159(m2).
【重难点剖析】 此类题主要考查了平移的性质——平移后的图形与原图形大小、形状都不变,面积自然也不变.因此,在变式题中,①号区面积+②号区面积=②号区面积+③号区面积,所以①号区面积=③号区面积.这类题的特点往往是声东击西,所以解题的对策就是转移目标.
【典例3】现一块白色正方形手帕,它的边长是18cm,上面横、竖各有两道红条,如图所示,红条的宽是2cm,怎样利用平移的知识,求出白色部分的面积?
【解析】将黑条平移到边缘,则白色部分的边长为18-2×2=14,
白色部分的面积为14×14=196(cm2).
【变式一】如图,由两个大小相同的正方形拼成一个长方形,正方形的边长是5,图中的阴影部分是有半径为5的圆弧和正方形的边围成的,求阴影部分的面积.
【解析】 由图形可知,将右边正方形中的阴影部分向左平移5个单位,正好与左边正方形中空白部分重合,所以图中阴影部分的面积恰好等于一个正方形的面积,故阴影部分的面积=5×5=25(平方单位).
【变式二】如图,在长为50m,宽为22m的长方形地面上修筑宽度都为2m的道路,余下的部分种植花草,求种植花草部分的面积.
【解析】如图,将几条2米宽的 小路分别平移到大长方形的上边缘和左边缘,则种植花草部分汇集成一个长方形,显然,这个长方形的长为48米,宽为20 米,所以,种植花草部分的面积为48×20=960平方米。
【重难点剖析】 此类题主要考查了图形的平移及平移的性质,关键是如何将不规则图形化为规则图形,或者将分散的部分化成一个整体,具体的做法是,把一个图形的整体或部分沿某一直线方向移动,得到一个新的图形,要求新图形与原图形的面积大小完全相同.
