人教版数学八年级下册 20.3体质健康测试中的数据分析 同步训练 (含解析)
文档属性
| 名称 | 人教版数学八年级下册 20.3体质健康测试中的数据分析 同步训练 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 194.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 15:52:55 | ||
图片预览



文档简介
20.3体质健康测试中的数据分析
一、单选题
1.甲、乙、丙、丁四名射击运动员参加射击预选赛,他们射击成绩的平均环数 及方差 如下表所示,若要选出一个成绩较好且状态稳定的运动员去参赛,那么应选运动员( )
甲 乙 丙 丁
8 9 9 8
1 1.1 1.2 1.3
A.甲 B.乙 C.丙 D.丁
2.某单位采购了5箱苹果,得到每箱质量各不相同的五个数据.登记入帐时将最小的数据又少写了1,则计算结果不受影响的是( )
A.中位数 B.平均数 C.方差 D.标准差
3.某数学兴趣小组为了了解本班学生一周课外阅读的时间,随机调查5名学生,并将所得数据整理如表:
学生 1 2 3 4 5
一周课外阅读时间(小时) 7 5 4 □ 8
表中有一个数字被污染后而模糊不清,但曾计算得该组数据的平均数为6,则这组数据的方差和中位数分别为( )
A.2,6 B.1.5,4 C.2,4 D.6,6
4.如表是某次射击比赛中10名选手的射击成绩(环):
射击成绩(环) 6 7 8 9 10
人数(人) 1 2 4 2 1
关于这10名选手的射击环数,下列说法错误的是( )
A.众数是8 B.中位数是5 C.平均数是8 D.方差是1.2
5.在一次演讲比赛中,七位评委为某位选手打出的分数如下:95,94,96,99,93,97,90(单位:分).若去掉一个最高分和一个最低分.则去掉前与去掉后没有改变的一个统计量是( )
A.平均分 B.方差 C.极差 D.中位数
6.某校为了解学生的课外阅读情况,随机抽取了一个班级的学生,对他们一周的读书时间进行了统计,统计数据如表所示:
读书时间(小时) 7 8 9 10 11
学生人数 6 10 9 8 7
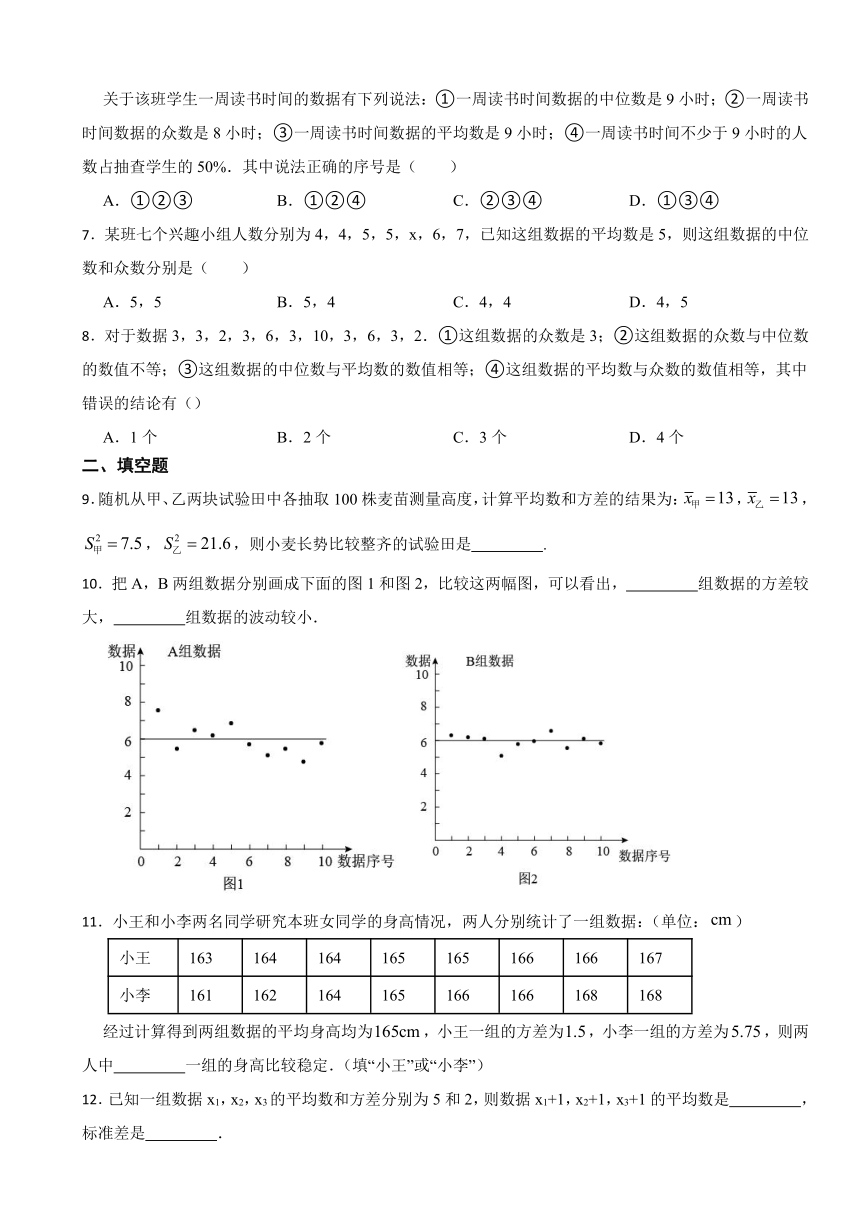
关于该班学生一周读书时间的数据有下列说法:①一周读书时间数据的中位数是9小时;②一周读书时间数据的众数是8小时;③一周读书时间数据的平均数是9小时;④一周读书时间不少于9小时的人数占抽查学生的50%.其中说法正确的序号是( )
A.①②③ B.①②④ C.②③④ D.①③④
7.某班七个兴趣小组人数分别为4,4,5,5,x,6,7,已知这组数据的平均数是5,则这组数据的中位数和众数分别是( )
A.5,5 B.5,4 C.4,4 D.4,5
8.对于数据3,3,2,3,6,3,10,3,6,3,2.①这组数据的众数是3;②这组数据的众数与中位数的数值不等;③这组数据的中位数与平均数的数值相等;④这组数据的平均数与众数的数值相等,其中错误的结论有()
A.1个 B.2个 C.3个 D.4个
二、填空题
9.随机从甲、乙两块试验田中各抽取100株麦苗测量高度,计算平均数和方差的结果为:,,,,则小麦长势比较整齐的试验田是 .
10.把A,B两组数据分别画成下面的图1和图2,比较这两幅图,可以看出, 组数据的方差较大, 组数据的波动较小.
11.小王和小李两名同学研究本班女同学的身高情况,两人分别统计了一组数据:(单位:)
小王 163 164 164 165 165 166 166 167
小李 161 162 164 165 166 166 168 168
经过计算得到两组数据的平均身高均为,小王一组的方差为,小李一组的方差为,则两人中 一组的身高比较稳定.(填“小王”或“小李”)
12.已知一组数据x1,x2,x3的平均数和方差分别为5和2,则数据x1+1,x2+1,x3+1的平均数是 ,标准差是 .
三、解答题
13.随着移动计算技术和无线网络的快速发展,移动学习方式越来越引起人们的关注,某校计划将这种学习方式应用到教育学中,从全校1500名学生中随机抽取了部分学生,对其家庭中拥有的移动设备的情况进行调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(2)求本次调查获取的样本数据的众数、中位数和平均数;
(3)根据样本数据,估计该校1500名学生家庭中拥有3台移动设备的学生人数.
14.某社区为了增强居民节约用水的意识,随机调查了部分家庭一年的月均用水量(单位:t).根据调查结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(Ⅰ)本次接受调查的家庭个数为 ,图①中m的值为 ;
(Ⅱ)求统计的这组月均用水量数据的平均数、众数和中位数.
15.为了解我县A,B两个乡镇板材企业第一季度的收入情况,从这两个乡镇的板材企业中,各随机抽取了25家板材企业,获得了它们第一季度收入(单位:百万元)的数据,并对数据进行整理、描述和分析.下面给出了部分信息.
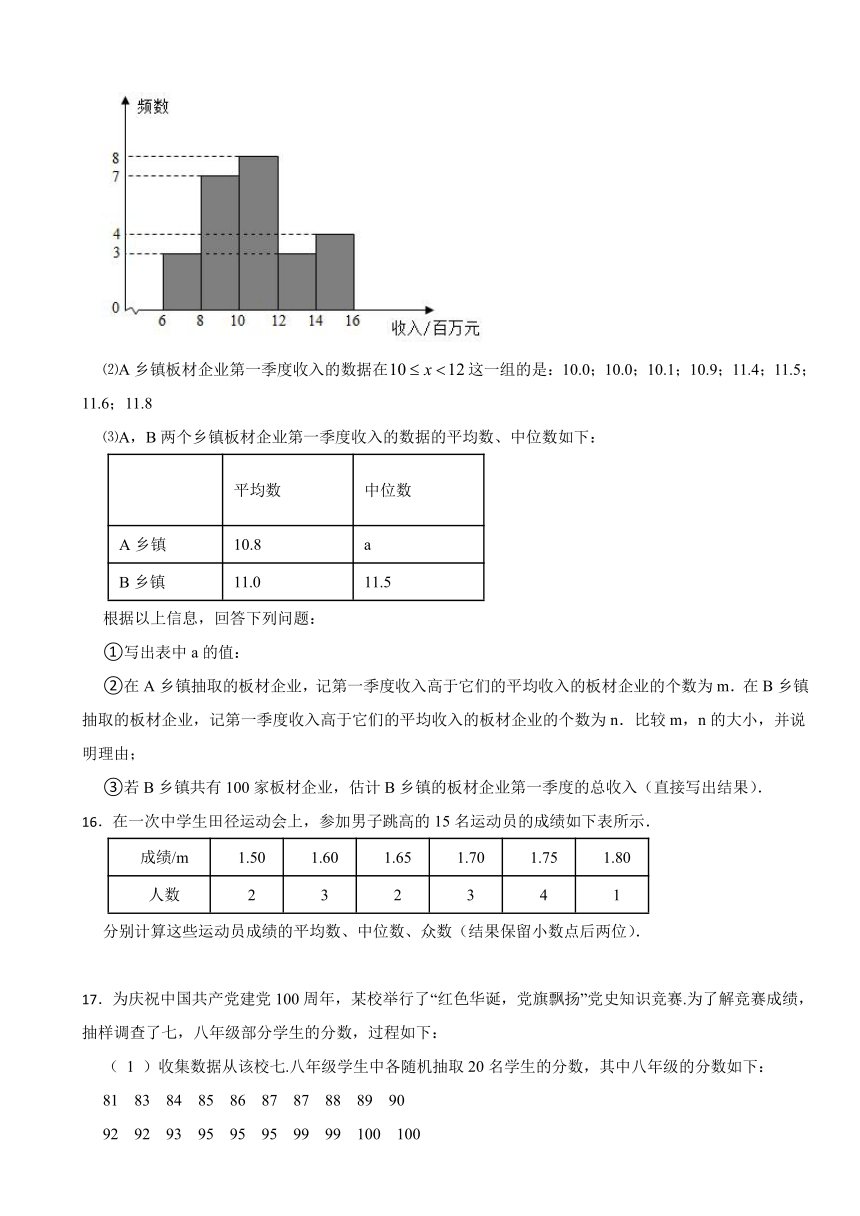
⑴A乡镇板材企业第一季度收入的数据的频数分布直方图如下图(数据分成5组:):
⑵A乡镇板材企业第一季度收入的数据在这一组的是:10.0;10.0;10.1;10.9;11.4;11.5;11.6;11.8
⑶A,B两个乡镇板材企业第一季度收入的数据的平均数、中位数如下:
平均数 中位数
A乡镇 10.8 a
B乡镇 11.0 11.5
根据以上信息,回答下列问题:
①写出表中a的值:
②在A乡镇抽取的板材企业,记第一季度收入高于它们的平均收入的板材企业的个数为m.在B乡镇抽取的板材企业,记第一季度收入高于它们的平均收入的板材企业的个数为n.比较m,n的大小,并说明理由;
③若B乡镇共有100家板材企业,估计B乡镇的板材企业第一季度的总收入(直接写出结果).
16.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示.
成绩/m 1.50 1.60 1.65 1.70 1.75 1.80
人数 2 3 2 3 4 1
分别计算这些运动员成绩的平均数、中位数、众数(结果保留小数点后两位).
17.为庆祝中国共产党建党100周年,某校举行了“红色华诞,党旗飘扬”党史知识竞赛.为了解竞赛成绩,抽样调查了七,八年级部分学生的分数,过程如下:
( 1 )收集数据从该校七.八年级学生中各随机抽取20名学生的分数,其中八年级的分数如下:
81 83 84 85 86 87 87 88 89 90
92 92 93 95 95 95 99 99 100 100
( 2 )整理、描述数据按如下分段整理描述样本数据:
分数 人数 年级
七年级 4 6 2 8
八年级 3 4 7
( 3 )分析数据两组样本数据的平均数、中位数、众数、方差如下表所示:
年级 平均数 中位数 众数 方差
七年级 91 89 97 40.9
八年级 91 33.2
根据以上提供的信息,解答下列问题:
①填空: , , ;
②样本数据中,七年级甲同学和八年级乙同学的分数都为90分, 同学的分数在本年级抽取的分数中从高到低排序更靠前(填“甲”或“乙”):
③从样本数据分析来看,分数较整齐的是 年级(填“七”或“八”);
④如果七年级共有400人参赛,则该年级约有 人的分数不低于95分.
18.某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡,根据它们的质量(单位: ),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
(Ⅰ)图①中 的值为_▲__;
(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ) 根据样本数据,估计这2500只鸡中,质量为 的约有多少只?
答案解析部分
1.【答案】B
【解析】【解答】解:由题意可知,甲、乙、丙、丁中,乙、丙的平均数最大,为9
∵1<1.1<1.2<1.3
∴乙的方差比丙的方差小
∴选择乙更为合适
故答案为:B.
【分析】平均数越大,成绩越好,方差越小成绩波动越小,据此即可得出答案.
2.【答案】A
【解析】【解答】解:登记入帐时将最小的数据又少写了1,计算结果不受影响的是中位数,
故答案为:A.
【分析】由于中位数不受极端值的影响,根据中位数的定义解答即可.
3.【答案】A
【解析】【解答】解:∵这组数据的平均数为6,
∴模糊不清的数是:6×5﹣7﹣5﹣4﹣8=6,
将数据重新排列为4、5、6、7、8,
所以这组数据的中位数为6,
则这组数据的方差为
=2;
故答案为:A.
【分析】先由平均数的公式计算出模糊不清的值,再根据中位数和方差的公式计算即可.
4.【答案】B
【解析】【解答】解:这组数据中8出现次数最多,即众数为8;
其中位数是第5、6个数据的平均数,故其中位数为;
平均数为,
方差为,
故答案为:B.
【分析】根据众数、中位数、平均数及方差的定义进行计算可得结论。
5.【答案】D
【解析】【解答】去掉前平均数:
去掉后平均数:
去掉前方差:
去掉后方差:
去掉前极差:
去掉后极差:
去掉前的中位数是: 90,93,94,95,96,97,99 是95
去掉后的中位数:93,94,95,96,97也是95,
所以中位数没变
故答案为:D.
【分析】根据平均分,方差,极差和中位数的定义计算求解即可。
6.【答案】A
【解析】【解答】解:由表格可得,该班有学生为:6+10+9+8+7=40人
第20、21位读书时间分别为9、9
∴该班学生一周读书时间的中位数和众数分别是:9、8,
一周读书时间数据的平均数为 =9小时
一周读书时间不少于9小时的人数占比为
故①②③符合题意;
故答案为:A.
【分析】根据表格中的数据可知该班有学生40人,从而求出 中位数 、 众数 、和平均数,再求出读书时间不少于9小时的人数的占比,得意解决。
7.【答案】B
【解析】【解答】解:∵,
∴x=4,
∴将数据由小到大重新排列为4,4,4,5,5,6,7,
∴这组数据的中位数为5,众数为4,
故答案为:B.
【分析】先利用平均数求出x的值,再利用中位数和众数的定义及计算方法求解即可。
8.【答案】C
【解析】【解答】解:数据3出现了6次,次数最多,所以众数是3,故①符合题意;
这组数据按照从小到大的顺序排列为2,2,3,3,3,3,3,3,6,6,10,处于中间位置的是3,所以中位数是3,故②不符合题意;
平均数为,故③、④不符合题意;
所以错误的结论有②、③、④,
故答案为:C.
【分析】根据众数,中位数,平均数的定义对每个结论一一判断即可。
9.【答案】甲
【解析】【解答】解:∵,,,,
∴,,
∵甲块试验田的方差小,
∴甲试验田小麦长势比较整齐.
故答案为:甲.
【分析】方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分别比较集中,各数偏离平均数越小,即波动越小,数据越稳定.
10.【答案】A;B
【解析】【解答】解:比较这两幅图,可以看出,A组数据的方差较大,B组数据的波动较小.
故答案为:A;B.
【分析】根据方差的性质:方差越大,数据波动越大。
11.【答案】小王
【解析】【解答】1.55.75,小王组方差相对小,说明相对稳定,故填:小王。
【分析】方差越小,数据波动性越小,数据越稳定。
12.【答案】6;
【解析】【解答】解:由题意得,,
∴x1+x2+x3=5×3=15,
∵[(x1﹣5)2+(x2﹣5)2+(x3﹣5)2]=2,
∴(x1+1+x2+1+x3+1)÷3(x1+x2+x3)+1=5+1=6,
∴S2[(x1+1﹣6)2+(x2+1﹣6)2+(x3+1﹣6)2],
[(x1﹣5)2+(x2﹣5)2+(x3﹣5)2],
=2,
∴S,
因此可得,数据x1+1,x2+1,x3+1的平均数是5+1=6,标准差为,
故答案为:6,.
【分析】利用平均数和标准差的定义及计算方法求解即可。
13.【答案】解:(Ⅰ)50|32;(Ⅱ)∵这组样本数据中,4出现了16次,出现次数最多, ∴这组数据的众数为4; ∵将这组数据从小到大排列,其中处于中间的两个数均为3,有 =3, ∴这组数据的中位数是3; 由条形统计图可得 =3.2, ∴这组数据的平均数是3.2. (Ⅲ)1500×28%=420(人). 答:估计该校学生家庭中;拥有3台移动设备的学生人数约为420人。
(1)50;32
(2)∵这组样本数据中,4出现了16次,出现次数最多,
∴这组数据的众数为4;
∵将这组数据从小到大排列,其中处于中间的两个数均为3,有 =3,
∴这组数据的中位数是3;
由条形统计图可得 =3.2,
∴这组数据的平均数是3.2.
(3)解:1500×28%=420(人).
答:估计该校学生家庭中;拥有3台移动设备的学生人数约为420人。
【解析】【解答】解:(1)本次接受随机抽样调查的学生人数为: =50(人),
∵ ×100=32%,
∴图①中m的值为32.
故答案为50、32;
【分析】(1)根据家庭中拥有1台移动设备的人数及所占的百分比可求出总人数,将拥有4台移动设备的人数除以总人数即可得m的值;
(2)根据众数、中位数、加权平均数的定义计算即可;
(3)将样本中拥有3台移动设备的学生人数所占的比例乘以1500即可。
14.【答案】解:(Ⅰ)50,20;
(Ⅱ)平均数:吨,
∵用水量6吨的家庭个数为16,最多,
∴众数=6吨,
∵一共50个数据,最中间的数据为第25和第26个数据,
∴中位数=(6+6)÷2=6吨.
答: 这组月均用水量数据的平均数为5.9吨,众数为6吨,中位数为6吨.
【解析】【解答】解:(Ⅰ)本次调查的家庭个数=8+12+16+10+4=50个,
m%=10÷50×100%=20%.
故答案为:50,20;
【分析】(Ⅰ)由条形图可知各个用水量的家庭个数,把所有家庭个数相加可求得本次调查的家庭个数,再用用水量为6.5吨的家庭个数除以总家庭个数,即可求出m的值;
(Ⅱ)利用加权平均数的计算公式,将数据代入公式计算即可求的组月均用水量数据的平均数,由条形统计图可知用水量6吨的家庭个数是16为最多,可求得众数,再由50个数据,最中间的数据为第25和第26个数据,将这两个数据求和再除以2,即可求出中位数.
15.【答案】解:①∵3+7<13,3+7+8=18>13,
∴中位数在这一组,
将A乡镇抽取的25家板材企业4月份的营业额在这一组的数据从小到大排列,得到10.0,10.0,10.1,10.9,11.4,11.5,11.6,11.8,
则中位数是第13个数,为10.1,即a = 10.1;
②由题意得m =5+3+4= 12(家),
∵B乡镇抽取的25家板材企业4月份的营业额的平均数是11.0,中位数是11.5,
∴所抽取的25家板材企业4月份营业额在11.5及以上的占一半,
则n的值至少为13,
∴m③B乡镇的板材企业第一季度的总收入约为:11.0 ×100 = 1100(百万元),
答:B乡镇200家板材企业4月份的总收入约为1100百万元.
【解析】【分析】①根据中位数的意义,求出A乡镇抽样25家板材企业第一季的营业额从小到大排列,得出处在第13位的数据即可;
②根据m、n所表示的意义,结合两个乡镇抽取的板材企业4月份的营业额的具体数据,得出将答案;
③根据B乡镇板材企业第一季度营业额的平均数以及企业的数量进行计算即可。
16.【答案】解:平均数为:
由成绩表知,正中间的数是1.70,故中位数为1.70
由于成绩为1.70米的学生人数最多,故众数这1.75
所以这些运动员成绩的平均数、中位数、众数分别为1.67,1.70,1.75.
【解析】【分析】利用平均数、中位数和众数的定义及计算方法求解即可。
17.【答案】6;91;95;甲;八;160
【解析】【解答】解:①、整理八年级20名学生的分数,分数在85≤x<90中的有:85、86、87、87、88、89,故a=6;
将20名学生成绩从低到高排列,第10名和第11名的成绩为90、92,
中位数为 ;
20名学生成绩中出现次数最多的为95,故众数为95.
②、七年级学生分数的中位数为89,七年级甲同学的成绩在中位数之前,名次靠前;
八年级的学生分数的中位数为91,八年级乙同学的成绩在中位数以后,名次靠后,
故甲同学的分数在本年级抽取的分数中从高到低排序更靠前;
③、八年级学生分数的方差小于七年级学生分数的方差,故八年级的分数较整齐;
④、抽取的七年级20名同学中分数不低于95分的人有8人,所占比为 ,故400名七年级学生分数不低于95分的学生约有: 人.
【分析】①整理八年级20名学生的分数,分数在85≤x<90中的人数,可得到a的值;利用中位数和众数的计算方法可求出b,c的值.
②利用表中七八年级的中位数进行分析,可得答案.
③比较方差的大小,可得答案.
④先求出抽取的七年级20名同学中分数不低于95分的人有8人,可求出其所占的比例,再列式计算可求出结果.
18.【答案】解:(Ⅰ)28;
(Ⅱ)观察条形统计图,
∵ ,
∴这组数据的平均数是1.52.
∵在这组数据中,1.8出现了16次,出现的次数最多,
∴这组数据的众数为1.8.
∵将这组数据按从小到大的顺序排列,其中处于中间的两个数都是1.5,有 ,
∴这组数据的中位数为1.5.
(Ⅲ)∵在所抽取的样本中,质量为 的数量占 .
∴由样本数据,估计这2500只鸡中,质量为 的数量约占 .
有 .
∴这2500只鸡中,质量为 的约有200只.
【解析】【解答】(1)m%=1-22%-10%-8%-32%=28%,故m=28;
故答案为:28;
【分析】(1)用整体1减去所有已知的百分比即可求出m的值;
(2)这组数据中出现次数最多的数据,就是这组数据的众数; 将这组数据按从小到大的顺序排列,其中处于中间的两个数的平均数就是这组数据的中位数;平均数利用加权平均数的定义计算即可;
(3)用总数乘以样本中2.0kg的鸡所占的比例即可得解.
一、单选题
1.甲、乙、丙、丁四名射击运动员参加射击预选赛,他们射击成绩的平均环数 及方差 如下表所示,若要选出一个成绩较好且状态稳定的运动员去参赛,那么应选运动员( )
甲 乙 丙 丁
8 9 9 8
1 1.1 1.2 1.3
A.甲 B.乙 C.丙 D.丁
2.某单位采购了5箱苹果,得到每箱质量各不相同的五个数据.登记入帐时将最小的数据又少写了1,则计算结果不受影响的是( )
A.中位数 B.平均数 C.方差 D.标准差
3.某数学兴趣小组为了了解本班学生一周课外阅读的时间,随机调查5名学生,并将所得数据整理如表:
学生 1 2 3 4 5
一周课外阅读时间(小时) 7 5 4 □ 8
表中有一个数字被污染后而模糊不清,但曾计算得该组数据的平均数为6,则这组数据的方差和中位数分别为( )
A.2,6 B.1.5,4 C.2,4 D.6,6
4.如表是某次射击比赛中10名选手的射击成绩(环):
射击成绩(环) 6 7 8 9 10
人数(人) 1 2 4 2 1
关于这10名选手的射击环数,下列说法错误的是( )
A.众数是8 B.中位数是5 C.平均数是8 D.方差是1.2
5.在一次演讲比赛中,七位评委为某位选手打出的分数如下:95,94,96,99,93,97,90(单位:分).若去掉一个最高分和一个最低分.则去掉前与去掉后没有改变的一个统计量是( )
A.平均分 B.方差 C.极差 D.中位数
6.某校为了解学生的课外阅读情况,随机抽取了一个班级的学生,对他们一周的读书时间进行了统计,统计数据如表所示:
读书时间(小时) 7 8 9 10 11
学生人数 6 10 9 8 7
关于该班学生一周读书时间的数据有下列说法:①一周读书时间数据的中位数是9小时;②一周读书时间数据的众数是8小时;③一周读书时间数据的平均数是9小时;④一周读书时间不少于9小时的人数占抽查学生的50%.其中说法正确的序号是( )
A.①②③ B.①②④ C.②③④ D.①③④
7.某班七个兴趣小组人数分别为4,4,5,5,x,6,7,已知这组数据的平均数是5,则这组数据的中位数和众数分别是( )
A.5,5 B.5,4 C.4,4 D.4,5
8.对于数据3,3,2,3,6,3,10,3,6,3,2.①这组数据的众数是3;②这组数据的众数与中位数的数值不等;③这组数据的中位数与平均数的数值相等;④这组数据的平均数与众数的数值相等,其中错误的结论有()
A.1个 B.2个 C.3个 D.4个
二、填空题
9.随机从甲、乙两块试验田中各抽取100株麦苗测量高度,计算平均数和方差的结果为:,,,,则小麦长势比较整齐的试验田是 .
10.把A,B两组数据分别画成下面的图1和图2,比较这两幅图,可以看出, 组数据的方差较大, 组数据的波动较小.
11.小王和小李两名同学研究本班女同学的身高情况,两人分别统计了一组数据:(单位:)
小王 163 164 164 165 165 166 166 167
小李 161 162 164 165 166 166 168 168
经过计算得到两组数据的平均身高均为,小王一组的方差为,小李一组的方差为,则两人中 一组的身高比较稳定.(填“小王”或“小李”)
12.已知一组数据x1,x2,x3的平均数和方差分别为5和2,则数据x1+1,x2+1,x3+1的平均数是 ,标准差是 .
三、解答题
13.随着移动计算技术和无线网络的快速发展,移动学习方式越来越引起人们的关注,某校计划将这种学习方式应用到教育学中,从全校1500名学生中随机抽取了部分学生,对其家庭中拥有的移动设备的情况进行调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(2)求本次调查获取的样本数据的众数、中位数和平均数;
(3)根据样本数据,估计该校1500名学生家庭中拥有3台移动设备的学生人数.
14.某社区为了增强居民节约用水的意识,随机调查了部分家庭一年的月均用水量(单位:t).根据调查结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(Ⅰ)本次接受调查的家庭个数为 ,图①中m的值为 ;
(Ⅱ)求统计的这组月均用水量数据的平均数、众数和中位数.
15.为了解我县A,B两个乡镇板材企业第一季度的收入情况,从这两个乡镇的板材企业中,各随机抽取了25家板材企业,获得了它们第一季度收入(单位:百万元)的数据,并对数据进行整理、描述和分析.下面给出了部分信息.
⑴A乡镇板材企业第一季度收入的数据的频数分布直方图如下图(数据分成5组:):
⑵A乡镇板材企业第一季度收入的数据在这一组的是:10.0;10.0;10.1;10.9;11.4;11.5;11.6;11.8
⑶A,B两个乡镇板材企业第一季度收入的数据的平均数、中位数如下:
平均数 中位数
A乡镇 10.8 a
B乡镇 11.0 11.5
根据以上信息,回答下列问题:
①写出表中a的值:
②在A乡镇抽取的板材企业,记第一季度收入高于它们的平均收入的板材企业的个数为m.在B乡镇抽取的板材企业,记第一季度收入高于它们的平均收入的板材企业的个数为n.比较m,n的大小,并说明理由;
③若B乡镇共有100家板材企业,估计B乡镇的板材企业第一季度的总收入(直接写出结果).
16.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示.
成绩/m 1.50 1.60 1.65 1.70 1.75 1.80
人数 2 3 2 3 4 1
分别计算这些运动员成绩的平均数、中位数、众数(结果保留小数点后两位).
17.为庆祝中国共产党建党100周年,某校举行了“红色华诞,党旗飘扬”党史知识竞赛.为了解竞赛成绩,抽样调查了七,八年级部分学生的分数,过程如下:
( 1 )收集数据从该校七.八年级学生中各随机抽取20名学生的分数,其中八年级的分数如下:
81 83 84 85 86 87 87 88 89 90
92 92 93 95 95 95 99 99 100 100
( 2 )整理、描述数据按如下分段整理描述样本数据:
分数 人数 年级
七年级 4 6 2 8
八年级 3 4 7
( 3 )分析数据两组样本数据的平均数、中位数、众数、方差如下表所示:
年级 平均数 中位数 众数 方差
七年级 91 89 97 40.9
八年级 91 33.2
根据以上提供的信息,解答下列问题:
①填空: , , ;
②样本数据中,七年级甲同学和八年级乙同学的分数都为90分, 同学的分数在本年级抽取的分数中从高到低排序更靠前(填“甲”或“乙”):
③从样本数据分析来看,分数较整齐的是 年级(填“七”或“八”);
④如果七年级共有400人参赛,则该年级约有 人的分数不低于95分.
18.某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡,根据它们的质量(单位: ),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
(Ⅰ)图①中 的值为_▲__;
(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ) 根据样本数据,估计这2500只鸡中,质量为 的约有多少只?
答案解析部分
1.【答案】B
【解析】【解答】解:由题意可知,甲、乙、丙、丁中,乙、丙的平均数最大,为9
∵1<1.1<1.2<1.3
∴乙的方差比丙的方差小
∴选择乙更为合适
故答案为:B.
【分析】平均数越大,成绩越好,方差越小成绩波动越小,据此即可得出答案.
2.【答案】A
【解析】【解答】解:登记入帐时将最小的数据又少写了1,计算结果不受影响的是中位数,
故答案为:A.
【分析】由于中位数不受极端值的影响,根据中位数的定义解答即可.
3.【答案】A
【解析】【解答】解:∵这组数据的平均数为6,
∴模糊不清的数是:6×5﹣7﹣5﹣4﹣8=6,
将数据重新排列为4、5、6、7、8,
所以这组数据的中位数为6,
则这组数据的方差为
=2;
故答案为:A.
【分析】先由平均数的公式计算出模糊不清的值,再根据中位数和方差的公式计算即可.
4.【答案】B
【解析】【解答】解:这组数据中8出现次数最多,即众数为8;
其中位数是第5、6个数据的平均数,故其中位数为;
平均数为,
方差为,
故答案为:B.
【分析】根据众数、中位数、平均数及方差的定义进行计算可得结论。
5.【答案】D
【解析】【解答】去掉前平均数:
去掉后平均数:
去掉前方差:
去掉后方差:
去掉前极差:
去掉后极差:
去掉前的中位数是: 90,93,94,95,96,97,99 是95
去掉后的中位数:93,94,95,96,97也是95,
所以中位数没变
故答案为:D.
【分析】根据平均分,方差,极差和中位数的定义计算求解即可。
6.【答案】A
【解析】【解答】解:由表格可得,该班有学生为:6+10+9+8+7=40人
第20、21位读书时间分别为9、9
∴该班学生一周读书时间的中位数和众数分别是:9、8,
一周读书时间数据的平均数为 =9小时
一周读书时间不少于9小时的人数占比为
故①②③符合题意;
故答案为:A.
【分析】根据表格中的数据可知该班有学生40人,从而求出 中位数 、 众数 、和平均数,再求出读书时间不少于9小时的人数的占比,得意解决。
7.【答案】B
【解析】【解答】解:∵,
∴x=4,
∴将数据由小到大重新排列为4,4,4,5,5,6,7,
∴这组数据的中位数为5,众数为4,
故答案为:B.
【分析】先利用平均数求出x的值,再利用中位数和众数的定义及计算方法求解即可。
8.【答案】C
【解析】【解答】解:数据3出现了6次,次数最多,所以众数是3,故①符合题意;
这组数据按照从小到大的顺序排列为2,2,3,3,3,3,3,3,6,6,10,处于中间位置的是3,所以中位数是3,故②不符合题意;
平均数为,故③、④不符合题意;
所以错误的结论有②、③、④,
故答案为:C.
【分析】根据众数,中位数,平均数的定义对每个结论一一判断即可。
9.【答案】甲
【解析】【解答】解:∵,,,,
∴,,
∵甲块试验田的方差小,
∴甲试验田小麦长势比较整齐.
故答案为:甲.
【分析】方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分别比较集中,各数偏离平均数越小,即波动越小,数据越稳定.
10.【答案】A;B
【解析】【解答】解:比较这两幅图,可以看出,A组数据的方差较大,B组数据的波动较小.
故答案为:A;B.
【分析】根据方差的性质:方差越大,数据波动越大。
11.【答案】小王
【解析】【解答】1.55.75,小王组方差相对小,说明相对稳定,故填:小王。
【分析】方差越小,数据波动性越小,数据越稳定。
12.【答案】6;
【解析】【解答】解:由题意得,,
∴x1+x2+x3=5×3=15,
∵[(x1﹣5)2+(x2﹣5)2+(x3﹣5)2]=2,
∴(x1+1+x2+1+x3+1)÷3(x1+x2+x3)+1=5+1=6,
∴S2[(x1+1﹣6)2+(x2+1﹣6)2+(x3+1﹣6)2],
[(x1﹣5)2+(x2﹣5)2+(x3﹣5)2],
=2,
∴S,
因此可得,数据x1+1,x2+1,x3+1的平均数是5+1=6,标准差为,
故答案为:6,.
【分析】利用平均数和标准差的定义及计算方法求解即可。
13.【答案】解:(Ⅰ)50|32;(Ⅱ)∵这组样本数据中,4出现了16次,出现次数最多, ∴这组数据的众数为4; ∵将这组数据从小到大排列,其中处于中间的两个数均为3,有 =3, ∴这组数据的中位数是3; 由条形统计图可得 =3.2, ∴这组数据的平均数是3.2. (Ⅲ)1500×28%=420(人). 答:估计该校学生家庭中;拥有3台移动设备的学生人数约为420人。
(1)50;32
(2)∵这组样本数据中,4出现了16次,出现次数最多,
∴这组数据的众数为4;
∵将这组数据从小到大排列,其中处于中间的两个数均为3,有 =3,
∴这组数据的中位数是3;
由条形统计图可得 =3.2,
∴这组数据的平均数是3.2.
(3)解:1500×28%=420(人).
答:估计该校学生家庭中;拥有3台移动设备的学生人数约为420人。
【解析】【解答】解:(1)本次接受随机抽样调查的学生人数为: =50(人),
∵ ×100=32%,
∴图①中m的值为32.
故答案为50、32;
【分析】(1)根据家庭中拥有1台移动设备的人数及所占的百分比可求出总人数,将拥有4台移动设备的人数除以总人数即可得m的值;
(2)根据众数、中位数、加权平均数的定义计算即可;
(3)将样本中拥有3台移动设备的学生人数所占的比例乘以1500即可。
14.【答案】解:(Ⅰ)50,20;
(Ⅱ)平均数:吨,
∵用水量6吨的家庭个数为16,最多,
∴众数=6吨,
∵一共50个数据,最中间的数据为第25和第26个数据,
∴中位数=(6+6)÷2=6吨.
答: 这组月均用水量数据的平均数为5.9吨,众数为6吨,中位数为6吨.
【解析】【解答】解:(Ⅰ)本次调查的家庭个数=8+12+16+10+4=50个,
m%=10÷50×100%=20%.
故答案为:50,20;
【分析】(Ⅰ)由条形图可知各个用水量的家庭个数,把所有家庭个数相加可求得本次调查的家庭个数,再用用水量为6.5吨的家庭个数除以总家庭个数,即可求出m的值;
(Ⅱ)利用加权平均数的计算公式,将数据代入公式计算即可求的组月均用水量数据的平均数,由条形统计图可知用水量6吨的家庭个数是16为最多,可求得众数,再由50个数据,最中间的数据为第25和第26个数据,将这两个数据求和再除以2,即可求出中位数.
15.【答案】解:①∵3+7<13,3+7+8=18>13,
∴中位数在这一组,
将A乡镇抽取的25家板材企业4月份的营业额在这一组的数据从小到大排列,得到10.0,10.0,10.1,10.9,11.4,11.5,11.6,11.8,
则中位数是第13个数,为10.1,即a = 10.1;
②由题意得m =5+3+4= 12(家),
∵B乡镇抽取的25家板材企业4月份的营业额的平均数是11.0,中位数是11.5,
∴所抽取的25家板材企业4月份营业额在11.5及以上的占一半,
则n的值至少为13,
∴m
答:B乡镇200家板材企业4月份的总收入约为1100百万元.
【解析】【分析】①根据中位数的意义,求出A乡镇抽样25家板材企业第一季的营业额从小到大排列,得出处在第13位的数据即可;
②根据m、n所表示的意义,结合两个乡镇抽取的板材企业4月份的营业额的具体数据,得出将答案;
③根据B乡镇板材企业第一季度营业额的平均数以及企业的数量进行计算即可。
16.【答案】解:平均数为:
由成绩表知,正中间的数是1.70,故中位数为1.70
由于成绩为1.70米的学生人数最多,故众数这1.75
所以这些运动员成绩的平均数、中位数、众数分别为1.67,1.70,1.75.
【解析】【分析】利用平均数、中位数和众数的定义及计算方法求解即可。
17.【答案】6;91;95;甲;八;160
【解析】【解答】解:①、整理八年级20名学生的分数,分数在85≤x<90中的有:85、86、87、87、88、89,故a=6;
将20名学生成绩从低到高排列,第10名和第11名的成绩为90、92,
中位数为 ;
20名学生成绩中出现次数最多的为95,故众数为95.
②、七年级学生分数的中位数为89,七年级甲同学的成绩在中位数之前,名次靠前;
八年级的学生分数的中位数为91,八年级乙同学的成绩在中位数以后,名次靠后,
故甲同学的分数在本年级抽取的分数中从高到低排序更靠前;
③、八年级学生分数的方差小于七年级学生分数的方差,故八年级的分数较整齐;
④、抽取的七年级20名同学中分数不低于95分的人有8人,所占比为 ,故400名七年级学生分数不低于95分的学生约有: 人.
【分析】①整理八年级20名学生的分数,分数在85≤x<90中的人数,可得到a的值;利用中位数和众数的计算方法可求出b,c的值.
②利用表中七八年级的中位数进行分析,可得答案.
③比较方差的大小,可得答案.
④先求出抽取的七年级20名同学中分数不低于95分的人有8人,可求出其所占的比例,再列式计算可求出结果.
18.【答案】解:(Ⅰ)28;
(Ⅱ)观察条形统计图,
∵ ,
∴这组数据的平均数是1.52.
∵在这组数据中,1.8出现了16次,出现的次数最多,
∴这组数据的众数为1.8.
∵将这组数据按从小到大的顺序排列,其中处于中间的两个数都是1.5,有 ,
∴这组数据的中位数为1.5.
(Ⅲ)∵在所抽取的样本中,质量为 的数量占 .
∴由样本数据,估计这2500只鸡中,质量为 的数量约占 .
有 .
∴这2500只鸡中,质量为 的约有200只.
【解析】【解答】(1)m%=1-22%-10%-8%-32%=28%,故m=28;
故答案为:28;
【分析】(1)用整体1减去所有已知的百分比即可求出m的值;
(2)这组数据中出现次数最多的数据,就是这组数据的众数; 将这组数据按从小到大的顺序排列,其中处于中间的两个数的平均数就是这组数据的中位数;平均数利用加权平均数的定义计算即可;
(3)用总数乘以样本中2.0kg的鸡所占的比例即可得解.
