数学人教A版(2019)选择性必修第一册1.1.2空间向量的数量积运算(共31张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.1.2空间向量的数量积运算(共31张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-15 08:14:48 | ||
图片预览






文档简介
(共31张PPT)
1.1
空间向量及其运算
第一章
1.1.2 空间向量的数量积运算
教学目标
1.理解空间两个向量夹角的定义.(直观想象)
2.掌握空间向量数量积的定义、性质、运算律,会求空间向量的数量积.(数学运算)
3.能够运用空间向量的数量积解决夹角与距离问题.(数学运算)
复习回顾
问题 (1)空间中共线向量的定理是什么?
(2)共面向量基本定理于是什么?
(3)四点共面的充要条件是什么?
向量共面的充要条件:如果两个向量不共线,则向量与向量共面的充要条件是存在唯一的有序实数对(x,y)使.
新课导入
导
平面向量及其线性运算
空间向量及线性运算
推广
平面向量数量积运算
空间向量数量积运算
推广
类比与转化
思
探究:类比平面向量的数量积运算,将平面向量数量积推广到空间数量积的运算
问题 回忆平面向量的知识,我们当时是如何研究它的数量积运算?
定义夹角
数量积定义
运算律
运用
思
问题 什么是平面向量的夹角?你能类比平面向量的夹角得出空间向量的夹角定义?
B
A
向量是可以平移的
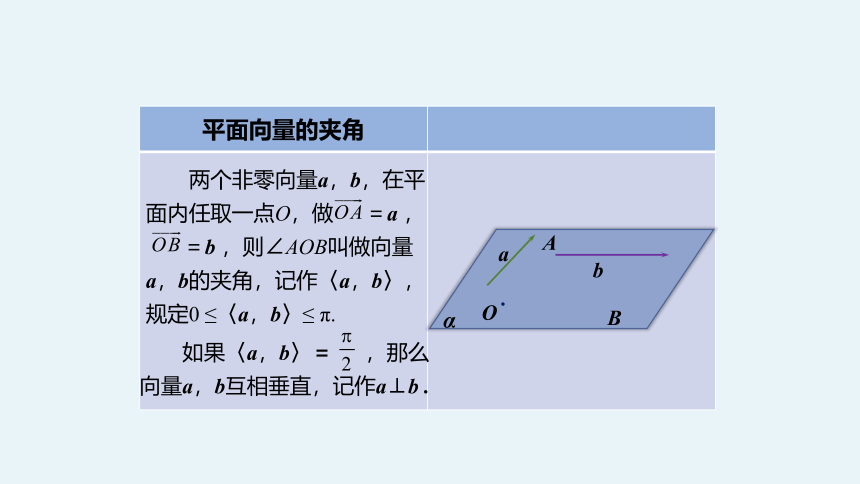
平面向量的夹角
两个非零向量a,b,在平面内任取一点O,做 =a ,
=b ,则∠AOB叫做向量
a,b的夹角,记作〈a,b〉,规定0 ≤〈a,b〉≤ π.
如果〈a,b〉= ,那么向量a,b互相垂直,记作a⊥b .
b
a
.
O
α
A
B
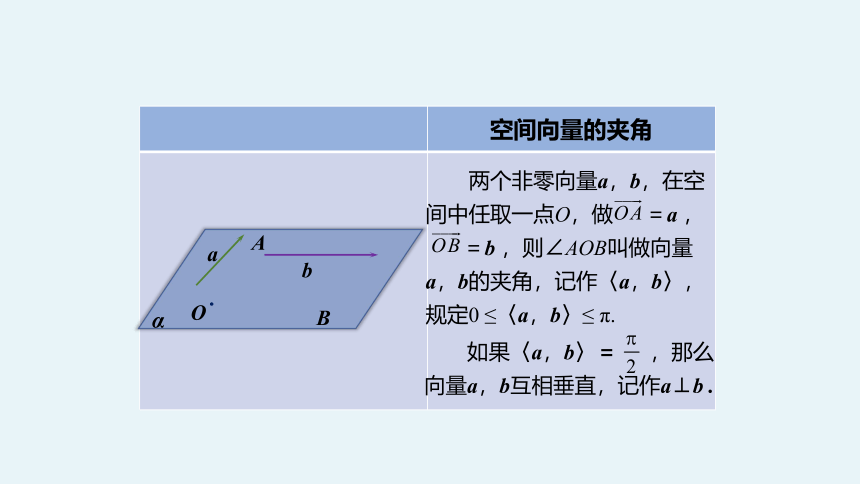
空间向量的夹角
两个非零向量a,b,在空间中任取一点O,做 =a ,
=b ,则∠AOB叫做向量
a,b的夹角,记作〈a,b〉,规定0 ≤〈a,b〉≤ π.
如果〈a,b〉= ,那么向量a,b互相垂直,记作a⊥b .
b
a
.
O
α
A
B
两个非零平面向量的数量积是一个实数,等于这两个向量的模和它们夹角余弦值的乘积,即:
a · b=|a||b|cos〈a,b〉.
特别地,零向量与任意向量的数量积为0.
思考 平面向量的数量积是什么?你能类比平面向量,给出空间向量数量积的运算吗?
空间两个向量的数量积性质
注:
性质②是证明两向量垂直的依据;
性质③是求向量的长度(模)的依据.
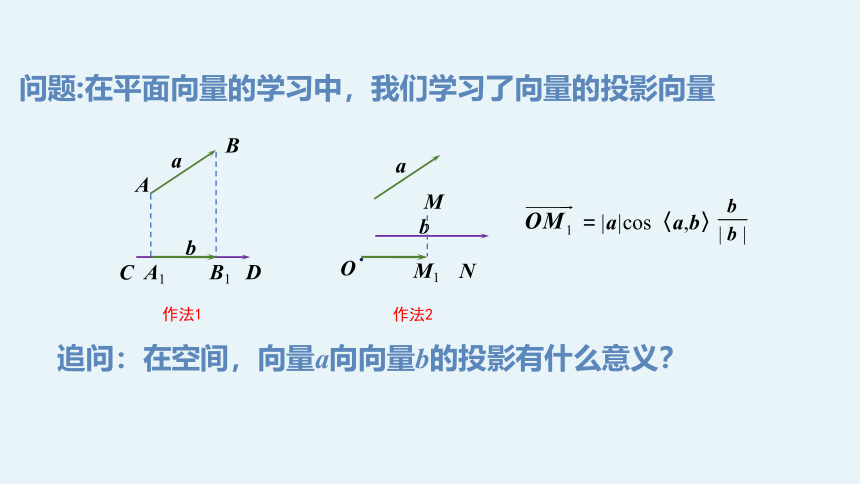
问题:在平面向量的学习中,我们学习了向量的投影向量
b
a
A
B
A1
D
C
B1
b
a
.
O
N
M
M1
=|a|cos〈a,b〉
作法1
作法2
追问:在空间,向量a向向量b的投影有什么意义?
A
B
(1)
(2)
(3)
问:类比平面向量数量积的运算律,空间向量数量积满足哪些运算律?
数乘向量与向量数量积的结合律 (λa)·b=λ(a·b), λ∈R
交换律 a·b=b·a
分配律 a·(b+c)=a·b+a·c
平面向量数量积的运算律:
空间向量?
同样满足上述运算律!
A
O
B
C
分配律a·(b+c)=a·b+a·c的证明
a
b
c
C’
A
B
C
O
题型三 用数量积求角度
总结
跟踪训练
探究
利用数量积求距离或长度
例 如图所示,在平行四边形ABCD中,AB=AC=1,∠ACD=90°,沿着它的对角线AC将△ACD折起,使AB与CD成60°角,求此时B,D间的距离.
【练习1】如图所示,在棱长为1的正四面体ABCD中,E,F分别是AB,AD的中点,求
【解】
(1)能否利用空间向量的数量积证明空间中两条直线垂直?
(2)能否利用空间向量的数量积求出空间中异面直线所成角?
(3)能否利用空间向量的数量积解决更多的立体几何中的问题?
课堂小练
B
A
B
回顾本节课的学习过程,你学到了什么?
1 数量积运算解决立体几何问题
(1) 求空间中两点间的距离或线段长度:求对应的向量的模
(2) 求空间中两条异面直线所成的角:求对应的两个向量的夹角
(3) 证明线线垂直问题:对应的两向量的数量积为零
2 类比平面向量的研究方法
类比
猜想
证明或转化
推广
感谢观看
1.1
空间向量及其运算
第一章
1.1.2 空间向量的数量积运算
教学目标
1.理解空间两个向量夹角的定义.(直观想象)
2.掌握空间向量数量积的定义、性质、运算律,会求空间向量的数量积.(数学运算)
3.能够运用空间向量的数量积解决夹角与距离问题.(数学运算)
复习回顾
问题 (1)空间中共线向量的定理是什么?
(2)共面向量基本定理于是什么?
(3)四点共面的充要条件是什么?
向量共面的充要条件:如果两个向量不共线,则向量与向量共面的充要条件是存在唯一的有序实数对(x,y)使.
新课导入
导
平面向量及其线性运算
空间向量及线性运算
推广
平面向量数量积运算
空间向量数量积运算
推广
类比与转化
思
探究:类比平面向量的数量积运算,将平面向量数量积推广到空间数量积的运算
问题 回忆平面向量的知识,我们当时是如何研究它的数量积运算?
定义夹角
数量积定义
运算律
运用
思
问题 什么是平面向量的夹角?你能类比平面向量的夹角得出空间向量的夹角定义?
B
A
向量是可以平移的
平面向量的夹角
两个非零向量a,b,在平面内任取一点O,做 =a ,
=b ,则∠AOB叫做向量
a,b的夹角,记作〈a,b〉,规定0 ≤〈a,b〉≤ π.
如果〈a,b〉= ,那么向量a,b互相垂直,记作a⊥b .
b
a
.
O
α
A
B
空间向量的夹角
两个非零向量a,b,在空间中任取一点O,做 =a ,
=b ,则∠AOB叫做向量
a,b的夹角,记作〈a,b〉,规定0 ≤〈a,b〉≤ π.
如果〈a,b〉= ,那么向量a,b互相垂直,记作a⊥b .
b
a
.
O
α
A
B
两个非零平面向量的数量积是一个实数,等于这两个向量的模和它们夹角余弦值的乘积,即:
a · b=|a||b|cos〈a,b〉.
特别地,零向量与任意向量的数量积为0.
思考 平面向量的数量积是什么?你能类比平面向量,给出空间向量数量积的运算吗?
空间两个向量的数量积性质
注:
性质②是证明两向量垂直的依据;
性质③是求向量的长度(模)的依据.
问题:在平面向量的学习中,我们学习了向量的投影向量
b
a
A
B
A1
D
C
B1
b
a
.
O
N
M
M1
=|a|cos〈a,b〉
作法1
作法2
追问:在空间,向量a向向量b的投影有什么意义?
A
B
(1)
(2)
(3)
问:类比平面向量数量积的运算律,空间向量数量积满足哪些运算律?
数乘向量与向量数量积的结合律 (λa)·b=λ(a·b), λ∈R
交换律 a·b=b·a
分配律 a·(b+c)=a·b+a·c
平面向量数量积的运算律:
空间向量?
同样满足上述运算律!
A
O
B
C
分配律a·(b+c)=a·b+a·c的证明
a
b
c
C’
A
B
C
O
题型三 用数量积求角度
总结
跟踪训练
探究
利用数量积求距离或长度
例 如图所示,在平行四边形ABCD中,AB=AC=1,∠ACD=90°,沿着它的对角线AC将△ACD折起,使AB与CD成60°角,求此时B,D间的距离.
【练习1】如图所示,在棱长为1的正四面体ABCD中,E,F分别是AB,AD的中点,求
【解】
(1)能否利用空间向量的数量积证明空间中两条直线垂直?
(2)能否利用空间向量的数量积求出空间中异面直线所成角?
(3)能否利用空间向量的数量积解决更多的立体几何中的问题?
课堂小练
B
A
B
回顾本节课的学习过程,你学到了什么?
1 数量积运算解决立体几何问题
(1) 求空间中两点间的距离或线段长度:求对应的向量的模
(2) 求空间中两条异面直线所成的角:求对应的两个向量的夹角
(3) 证明线线垂直问题:对应的两向量的数量积为零
2 类比平面向量的研究方法
类比
猜想
证明或转化
推广
感谢观看
