2022-2023学年鲁教版数学五四制九年级上册 3.3 二次函数y=ax2的图象与性质 (1)课件 (共23张PPT)
文档属性
| 名称 | 2022-2023学年鲁教版数学五四制九年级上册 3.3 二次函数y=ax2的图象与性质 (1)课件 (共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 639.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 14:06:40 | ||
图片预览








文档简介
(共23张PPT)
第三章 二次函数
3.3 二次函数y=ax2的图象与性质 第一课时
学 习 目 标
1.知道二次函数的图象是一条抛物线。
2、会用描点法画二次函数y=ax2的图象,并能比较y=-x2与y=x2的异同,理解a对二次函数图象的影响;理解二次函数y=ax2(a≠0)的性质。
c是常数,a≠0)
1.一般地,形如
2.我们学习过哪些函数?
y=ax +bx+c(a、b、
的函数叫做x的二次函数。
复习回顾
y=ax +bx+c(a≠0)
二次函数
y=kx+b (k≠0)
y=kx (k≠0)
一次函数
变量之间的关系
函数
反比例函数
正比例函数
y= (k≠0)
3.一次函数的图象是 。
4.反比例函数的图象是 。
双曲线
5.二次函数的图象是什么形状呢?
一条直线
(3)连线
(1)列表
用描点法画函数图象的主要步骤是:
(2)描点
6.通常怎样画一个函数的图象?
答:通常用描点法画一个函数的图象。
(1)观察y=x2的表达式,选择适当的x值,并计算相应的y值,完成下表:
画二次函数y=x2的图象
x … …
y … …
9
4
9
0
1
4
1
-3
-2
-1
0
1
2
3
新知讲解
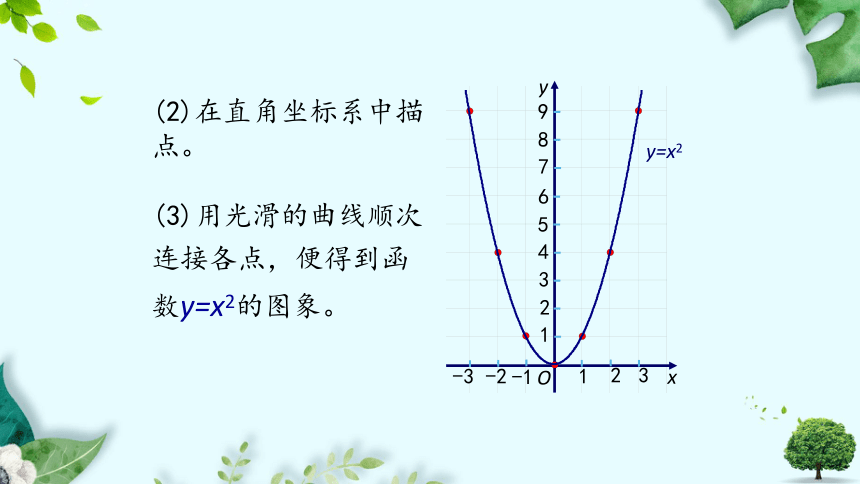
(2)在直角坐标系中描点。
(3)用光滑的曲线顺次连接各点,便得到函数y=x2的图象。
x
y
-1
-2
-3
O
1
2
3
3
2
1
6
5
4
9
8
7
y=x2
x
y
-1
-2
-3
O
1
2
3
3
2
1
6
5
4
9
8
7
y=x2
(1)你能描述图象的形状吗?
议一议
x
y
-1
-2
-3
O
1
2
3
3
2
1
6
5
4
9
8
7
y=x2
(1)你能描述图象的形状吗?
议一议
二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线y=x2。
x
y
-1
-2
-3
O
1
2
3
3
2
1
6
5
4
9
8
7
y=x2
(2)图象与x轴有交点 吗?如果有,交点坐标是什么?
有,(0,0)
x
y
-1
-2
-3
O
1
2
3
3
2
1
6
5
4
9
8
7
y=x2
(3)当x<0时,随着x值的增大, y的值如何变化?当x>0时呢?
当x<0 时,y随着x的增大而减小。
当x>0 时,y随着x的增大而增大。
(4)当x取什么值时,y的值最小?最小值是什么?你是如何知道的?
当x=0时,函数y的值最小,最小值是0。
可以观察图象,也可以分析表达式。
x
y
-1
-2
-3
O
1
2
3
3
2
1
6
5
4
9
8
7
y=x2
是,对称轴是y 轴。
(-2,4)和(2,4);
(-3,9)和(3,9)等等。
(-1,1)和(1,1);
(5)图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点。
对称点有很多,如:
x
y
-1
-2
-3
O
1
2
3
3
2
1
6
5
4
9
8
7
y=x2
二次函数y=x2的图象的顶点是原点,它是图象的最低点。
x
y
-1
-2
-3
O
1
2
3
3
2
1
6
5
4
9
8
7
y=x2
(6)图象与对称轴有交点吗?
抛物线与对称轴的交点叫做抛物线的顶点。
二次函数y=x2的图象是一条抛物线,它的特点是:
x
y
-1
-2
-3
O
1
2
3
3
2
1
6
5
4
9
8
7
y=x2
1.开口向上;
2.对称轴是y轴;
3.顶点是原点,它是图象的最低点。
作出二次函数y = -x2 的图象。
(1) 列表:
x … -3 -2 -1 0 1 2 3 …
y … …
-9
-4
-1
-1
-4
-9
0
(2)在直角坐标系中描点。
(3)用光滑的曲线顺次连接各点,便得到函数 y=-x2 的图象。
y
x
-1
-2
-3
O
1
2
3
-6
-7
-8
-3
-4
-5
-9
-1
-2
y=- x2
(1)二次函数 y=-x2 的图象是一条抛物线。
(2)图象与 x 轴交于原点(0,0)。
y
x
-1
-2
-3
O
1
2
3
-6
-7
-8
-3
-4
-5
-9
-1
-2
y=- x2
(3)当x <0时,y 随 x 的增大而增大;当x >0时,y 随 x 的增大而减小。
(4)当 x=0时,y最大值 = 0
(5)图象关于 y 轴对称。
y
x
-1
-2
-3
O
1
2
3
-6
-7
-8
-3
-4
-5
-9
-1
-2
y=- x2
(6)图象的顶点是原点,它是图象的最高点。
谢谢观赏
第三章 二次函数
3.3 二次函数y=ax2的图象与性质 第一课时
学 习 目 标
1.知道二次函数的图象是一条抛物线。
2、会用描点法画二次函数y=ax2的图象,并能比较y=-x2与y=x2的异同,理解a对二次函数图象的影响;理解二次函数y=ax2(a≠0)的性质。
c是常数,a≠0)
1.一般地,形如
2.我们学习过哪些函数?
y=ax +bx+c(a、b、
的函数叫做x的二次函数。
复习回顾
y=ax +bx+c(a≠0)
二次函数
y=kx+b (k≠0)
y=kx (k≠0)
一次函数
变量之间的关系
函数
反比例函数
正比例函数
y= (k≠0)
3.一次函数的图象是 。
4.反比例函数的图象是 。
双曲线
5.二次函数的图象是什么形状呢?
一条直线
(3)连线
(1)列表
用描点法画函数图象的主要步骤是:
(2)描点
6.通常怎样画一个函数的图象?
答:通常用描点法画一个函数的图象。
(1)观察y=x2的表达式,选择适当的x值,并计算相应的y值,完成下表:
画二次函数y=x2的图象
x … …
y … …
9
4
9
0
1
4
1
-3
-2
-1
0
1
2
3
新知讲解
(2)在直角坐标系中描点。
(3)用光滑的曲线顺次连接各点,便得到函数y=x2的图象。
x
y
-1
-2
-3
O
1
2
3
3
2
1
6
5
4
9
8
7
y=x2
x
y
-1
-2
-3
O
1
2
3
3
2
1
6
5
4
9
8
7
y=x2
(1)你能描述图象的形状吗?
议一议
x
y
-1
-2
-3
O
1
2
3
3
2
1
6
5
4
9
8
7
y=x2
(1)你能描述图象的形状吗?
议一议
二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线y=x2。
x
y
-1
-2
-3
O
1
2
3
3
2
1
6
5
4
9
8
7
y=x2
(2)图象与x轴有交点 吗?如果有,交点坐标是什么?
有,(0,0)
x
y
-1
-2
-3
O
1
2
3
3
2
1
6
5
4
9
8
7
y=x2
(3)当x<0时,随着x值的增大, y的值如何变化?当x>0时呢?
当x<0 时,y随着x的增大而减小。
当x>0 时,y随着x的增大而增大。
(4)当x取什么值时,y的值最小?最小值是什么?你是如何知道的?
当x=0时,函数y的值最小,最小值是0。
可以观察图象,也可以分析表达式。
x
y
-1
-2
-3
O
1
2
3
3
2
1
6
5
4
9
8
7
y=x2
是,对称轴是y 轴。
(-2,4)和(2,4);
(-3,9)和(3,9)等等。
(-1,1)和(1,1);
(5)图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点。
对称点有很多,如:
x
y
-1
-2
-3
O
1
2
3
3
2
1
6
5
4
9
8
7
y=x2
二次函数y=x2的图象的顶点是原点,它是图象的最低点。
x
y
-1
-2
-3
O
1
2
3
3
2
1
6
5
4
9
8
7
y=x2
(6)图象与对称轴有交点吗?
抛物线与对称轴的交点叫做抛物线的顶点。
二次函数y=x2的图象是一条抛物线,它的特点是:
x
y
-1
-2
-3
O
1
2
3
3
2
1
6
5
4
9
8
7
y=x2
1.开口向上;
2.对称轴是y轴;
3.顶点是原点,它是图象的最低点。
作出二次函数y = -x2 的图象。
(1) 列表:
x … -3 -2 -1 0 1 2 3 …
y … …
-9
-4
-1
-1
-4
-9
0
(2)在直角坐标系中描点。
(3)用光滑的曲线顺次连接各点,便得到函数 y=-x2 的图象。
y
x
-1
-2
-3
O
1
2
3
-6
-7
-8
-3
-4
-5
-9
-1
-2
y=- x2
(1)二次函数 y=-x2 的图象是一条抛物线。
(2)图象与 x 轴交于原点(0,0)。
y
x
-1
-2
-3
O
1
2
3
-6
-7
-8
-3
-4
-5
-9
-1
-2
y=- x2
(3)当x <0时,y 随 x 的增大而增大;当x >0时,y 随 x 的增大而减小。
(4)当 x=0时,y最大值 = 0
(5)图象关于 y 轴对称。
y
x
-1
-2
-3
O
1
2
3
-6
-7
-8
-3
-4
-5
-9
-1
-2
y=- x2
(6)图象的顶点是原点,它是图象的最高点。
谢谢观赏
