2023年内蒙古自治区呼伦贝尔、兴安盟中考数学试题(含答案)
文档属性
| 名称 | 2023年内蒙古自治区呼伦贝尔、兴安盟中考数学试题(含答案) |

|
|
| 格式 | |||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 00:00:00 | ||
图片预览



文档简介
姓名 准考证号
2023 年呼伦贝尔市、兴安盟初中毕业生学业考试
数 学
温馨提示:
1. 本试卷共 6 页,满分 120 分。考试时间 120 分钟。
2. 答卷前务必将自己的姓名、准考证号、座位号填写在答题卡上;选择题答案选出后,请
用 2B 铅笔把答题卡上对应题目的答案标号(ABCD)涂黑,如需改动,请先用橡皮擦拭干净,
再改涂其他答案;非选择题,请用 0.5 毫米的黑色字迹签字笔直接答在答题卡上。在试卷上作
答无效。
3. 请将姓名与准考证号填写在本试卷相应位置上。
4. 考试结束,将试卷、答题卡和草稿纸一并交回。
一、选择题(下列各题的四个选项中只有一个正确. 共 12 小题,每小题 3 分,共 36 分)
1. 5 的倒数是
A 1. B 1. C.5 D. 5
5 5
2.由大小相同的正方体搭成的几何体如图所示,其左视图是
A B C D
3.下列运算正确的是
A. 3 2 3 2 6 B. 3 a2 a6
C 1 1 2 1 b 1. D.
2a a 3a 3ab 3a b 2
4.将一副直角三角板按如图所示的方式摆放,点 C 在 FD 的延长线上,且 AB∥FC,则∠CBD
的度数为
A.10° B.15°
C.20° D.25°
呼伦贝尔市、兴安盟初中毕业生学业考试数学试卷 第 1 页(共 6 页)
{#{QQABAQAUogAgAhBAAQgCQQ3QCkAQkBGAAIoGwEAEMAIBABFABAA=}#}
5.不等式 x 1< 5 的正整数解的个数有
A.3 个 B.4 个 C.5 个 D.6 个
6.下列命题正确的是
A.“经过有交通信号灯的路口,遇到红灯”是必然事件
B.3.14 精确到十分位
C.点( 2 , 3)关于 x轴的对称点坐标是( 2 ,3)
D 2 2.甲、乙两人参加环保知识竞赛,他们的平均成绩相同,方差分别是 S甲=2.25,S乙 =1.81,
则甲成绩比乙的稳定
7.某校举行篮球赛,每场比赛都要分出胜负,每队胜一场得 2 分,负一场得 1 分. 某队在 12
场比赛中得 20 分. 设该队胜 x场,负 y场,则根据题意,列出关于 x、y的二元一次方程组
正确的是
x y 20 x y 12A. B.
x 2y 12 x 2y 20
x y 20 x y 12C. D.
2x y 12
2x y 20
8.若实数 m,n是一元二次方程 x2 2 x 3 =0 的两个根,且 m<n,则点(m,n)所在象限为
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.如图,在菱形 ABCD 中,AB=4,∠A=120°,顺次连接菱形 ABCD 各边中点 E、F、G、H,
则四边形 EFGH 的周长为
A. 4 2 3 B.6 2 3
C. 4 4 3 D.6 4 3
10 k.如图,直线 y ax (b a 0)与双曲线 y (k 0)交于点 A( 2 , 4)和点 B(m , 2),
x
则不等式 0 ax b k 的解集是
x
A. 2B. 2 C.x< 2 或 0D. 2 4
呼伦贝尔市、兴安盟初中毕业生学业考试数学试卷 第 2 页(共 6 页)
{#{QQABAQAUogAgAhBAAQgCQQ3QCkAQkBGAAIoGwEAEMAIBABFABAA=}#}
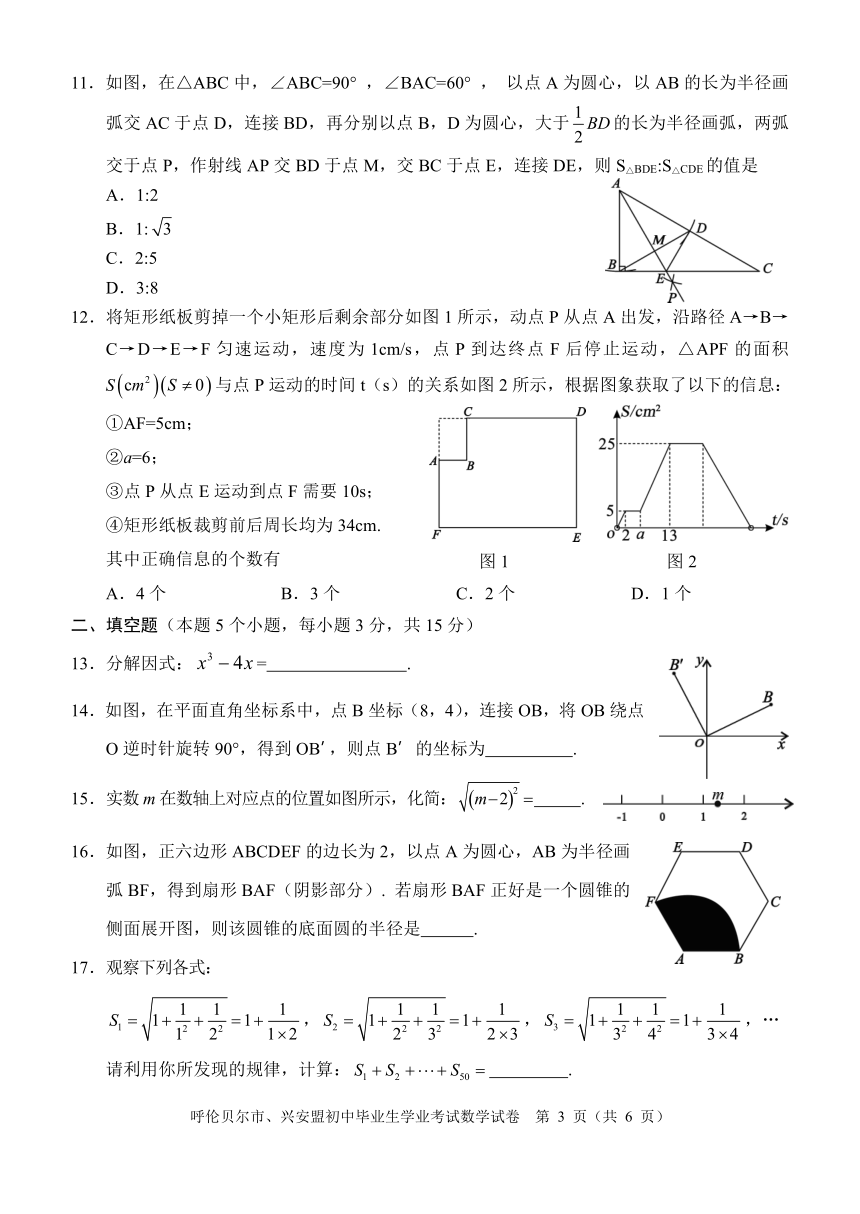
11.如图,在△ABC 中,∠ABC=90° ,∠BAC=60° , 以点 A 为圆心,以 AB 的长为半径画
弧交 AC 于点 D 1,连接 BD,再分别以点 B,D 为圆心,大于 BD的长为半径画弧,两弧
2
交于点 P,作射线 AP 交 BD 于点 M,交 BC 于点 E,连接 DE,则 S△BDE:S△CDE的值是
A.1:2
B.1: 3
C.2:5
D.3:8
12.将矩形纸板剪掉一个小矩形后剩余部分如图 1 所示,动点 P 从点 A 出发,沿路径 A→B→
C→D→E→F 匀速运动,速度为 1cm/s,点 P 到达终点 F 后停止运动,△APF 的面积
S cm2 S 0 与点 P 运动的时间 t(s)的关系如图 2 所示,根据图象获取了以下的信息:
①AF=5cm;
②a=6;
③点 P 从点 E 运动到点 F 需要 10s;
④矩形纸板裁剪前后周长均为 34cm.
其中正确信息的个数有 图 1 图 2
A.4 个 B.3 个 C.2 个 D.1 个
二、填空题(本题 5 个小题,每小题 3 分,共 15 分)
13.分解因式: x3 4x = .
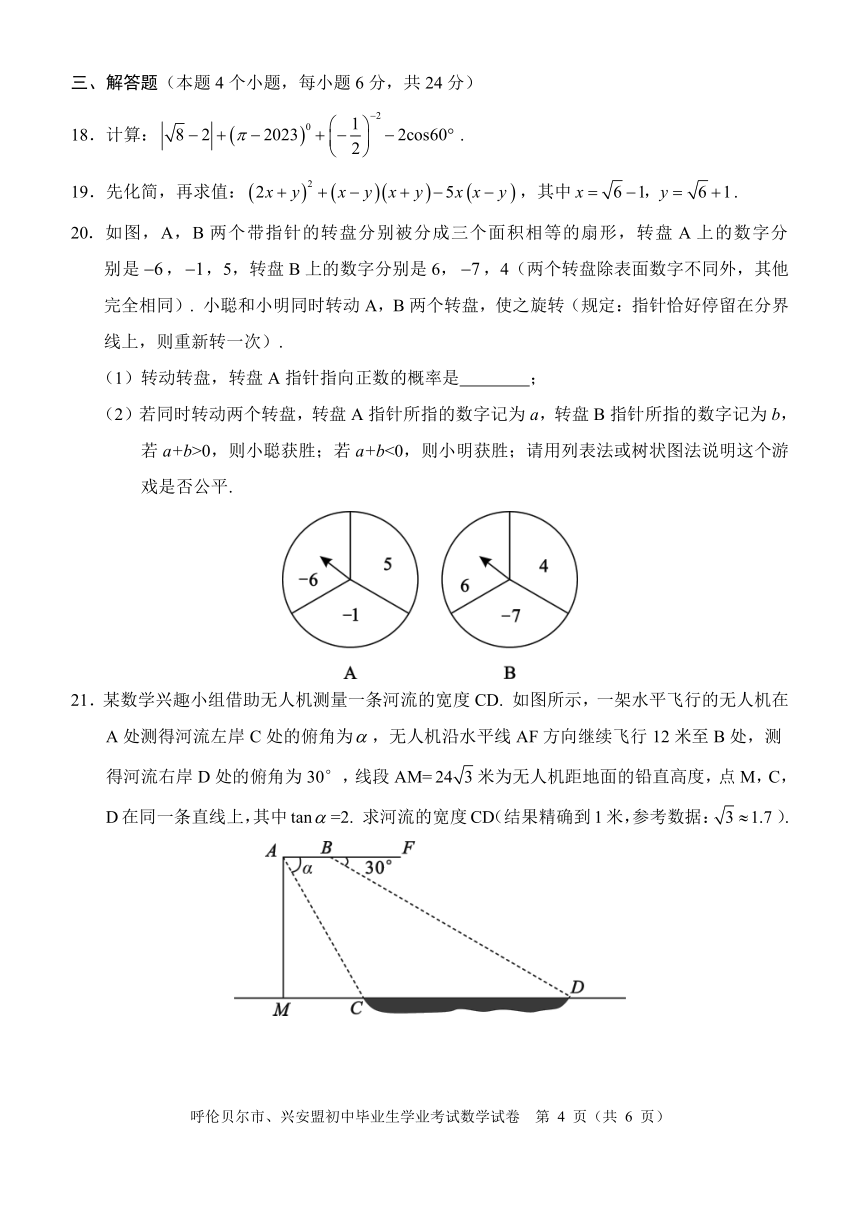
14.如图,在平面直角坐标系中,点 B 坐标(8,4),连接 OB,将 OB 绕点
O 逆时针旋转 90°,得到 OB’,则点 B’的坐标为 .
15.实数m 2在数轴上对应点的位置如图所示,化简: m 2 .
16.如图,正六边形 ABCDEF 的边长为 2,以点 A 为圆心,AB 为半径画
弧 BF,得到扇形 BAF(阴影部分). 若扇形 BAF 正好是一个圆锥的
侧面展开图,则该圆锥的底面圆的半径是 .
17.观察下列各式:
S 1 1 1 1 1 S 1 1 1 1 1 1 1 11 2 2 , 2 2 2 , S 1 1 ,…1 2 1 2 2 3 2 3 3 32 42 3 4
请利用你所发现的规律,计算: S1 S2 S50 .
呼伦贝尔市、兴安盟初中毕业生学业考试数学试卷 第 3 页(共 6 页)
{#{QQABAQAUogAgAhBAAQgCQQ3QCkAQkBGAAIoGwEAEMAIBABFABAA=}#}
三、解答题(本题 4 个小题,每小题 6 分,共 24 分)
2
18.计算: 8 2 2023 0 1 2cos60 .
2
19 2.先化简,再求值: 2x y x y x y 5x x y ,其中 x 6 1,y 6 1 .
20.如图,A,B 两个带指针的转盘分别被分成三个面积相等的扇形,转盘 A 上的数字分
别是 6, 1,5,转盘 B 上的数字分别是 6, 7,4(两个转盘除表面数字不同外,其他
完全相同). 小聪和小明同时转动 A,B 两个转盘,使之旋转(规定:指针恰好停留在分界
线上,则重新转一次).
(1)转动转盘,转盘 A 指针指向正数的概率是 ;
(2)若同时转动两个转盘,转盘 A 指针所指的数字记为 a,转盘 B 指针所指的数字记为 b,
若 a+b>0,则小聪获胜;若 a+b<0,则小明获胜;请用列表法或树状图法说明这个游
戏是否公平.
21.某数学兴趣小组借助无人机测量一条河流的宽度 CD. 如图所示,一架水平飞行的无人机在
A 处测得河流左岸 C 处的俯角为 ,无人机沿水平线 AF 方向继续飞行 12 米至 B 处,测
得河流右岸 D 处的俯角为 30°,线段 AM= 24 3 米为无人机距地面的铅直高度,点 M,C,
D在同一条直线上,其中 tan =2. 求河流的宽度CD(结果精确到 1米,参考数据: 3 1.7 ).
呼伦贝尔市、兴安盟初中毕业生学业考试数学试卷 第 4 页(共 6 页)
{#{QQABAQAUogAgAhBAAQgCQQ3QCkAQkBGAAIoGwEAEMAIBABFABAA=}#}
四、(本题 7 分)
22.为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学
生成绩进行统计,按成绩分为如下 5 组(满分 100 分),A 组:75≤x<80,B 组:80≤x<85,
C 组:85≤x<90,D 组:90≤x<95,E 组:95≤x≤100,并绘制了如下不完整的统计图表.
请结合统计图表,解答如下问题:
(1)本次调查的样本容量为 ,学生成绩统计表中 m= ;
(2)所抽取学生成绩的中位数落在 组;
(3)求出扇形统计图中“E”所在扇形的圆心角度数;
(4)若成绩在 90 分及以上为优秀,学校共有 2000 名学生,估计该校成绩优秀的学生有多少名?
学生成绩统计表 学生成绩统计图
组别 成绩 x 频数
A 75≤x<80 20
B 80≤x<85 m
C 85≤x<90 144
D 90≤x<95 45
E 95≤x≤100 n
五、(本题 7 分)
23.如图,AB 是⊙O 的直径,E 为⊙O 上的一点,点C 是 AE的中点,连接 BC,过点 C 的直线
垂直于 BE 的延长线于点 D,交 BA 的延长线于点 P.
(1)求证:PC 为⊙O 的切线;
(2)若 PC= 2 2 BO,PB=10,求 BE 的长.
六、(本题 9 分)
24.端午节吃粽子是中华民族的传统习俗. 市场上豆沙粽礼盒的进价比肉粽礼盒的进价每盒便
宜 10 元,某商家用 2500 元购进的肉粽和用 2000 元购进的豆沙粽盒数相同.
(1)求每盒肉粽和每盒豆沙粽的进价;
(2)商家计划只购买豆沙粽礼盒销售,经调查了解到有 A,B 两个厂家可供选择,两个厂
家针对价格相同的豆沙粽礼盒给出了不同的优惠方案:
A 厂家:一律打 8 折出售.
B 厂家:若一次性购买礼盒数量超过 25 盒,超过的部分打 7 折.
该商家计划购买豆沙粽礼盒 x盒,设去 A 厂家购买应付 y1 元,
去 B 厂家购买应付 y 元,其函数图象如图所示:
2
①分别求出 y1 , y2 与 x之间的函数关系;
②若该商家只在一个厂家购买,怎样买划算?
呼伦贝尔市、兴安盟初中毕业生学业考试数学试卷 第 5 页(共 6 页)
{#{QQABAQAUogAgAhBAAQgCQQ3QCkAQkBGAAIoGwEAEMAIBABFABAA=}#}
七、(本题 9 分)
25.已知正方形 ABCD,E 是对角线 AC 上一点.
(1)如图 1,连接 BE,DE. 求证:△ABE≌△ADE;
(2)如图 2,F 是 DE 延长线上一点,DF 交 AB 于点 G,BF⊥BE.
判断△FBG 的形状并说明理由;
3 AE( )在第(2)题的条件下,BE=BF=2. 求 的值.
AB
图 1 图 2
八、(本题 13 分)
26.如图,在平面直角坐标系中,抛物线 y = x2 bx c与 x轴的交点分别为 A 和 B
(1,0)(点A在点 B的左侧),与 y轴交于点C(0,3),点 P 是直线AC 上方抛物线上一动点.
(1)求抛物线的解析式;
(2)如图 1,过点 P 做 x轴平行线交 AC 于点 E,过点 P 做 y 轴平行线交 x 轴于点 D,
求 PE+PD 的最大值及点 P 的坐标;
(3)如图 2,设点 M 为抛物线对称轴上一动点,当点 P,点 M 运动时,在坐标轴上确定点N,
使四边形 PMCN 为矩形,求出所有符合条件的点 N 的坐标.
图 1 图 2 备用图
呼伦贝尔市、兴安盟初中毕业生学业考试数学试卷 第 6 页(共 6 页)
{#{QQABAQAUogAgAhBAAQgCQQ3QCkAQkBGAAIoGwEAEMAIBABFABAA=}#}
2023年呼伦贝尔市、兴安盟初中毕业生学业考试
数学答案及评分标准
一、选择题(每小题 3分,共 36分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A B D B A C D B C B A C
二、填空题(每小题 3分,共 15分)
x(x 2)(x 2) - 2 m 2 50 5013 . 14.( 4, 8) 15. 16. 17.
3 51
三、解答题(每小题 6分,共 24分)
18.解:原式 8 2 1 1 4 2 …………(4分)
2
2 2 2 1 4 1
2 2 2 …………(6分)
19.解:原式=4x2+4xy+y2+x2-y2-5x2+5xy
=9xy …………(4分)
当x 6 1, y 6 1时
原式 (9 6 1)( 6 1) 9(6 1) 45 …………(6分)
1
20.(1) …………(1分)
3
(2)解:列表得:
b a -6 -1 5
6 (-6,6) (-1,6) (5,6)
-7 (-6,-7) (-1,-7) (5,-7)
4 (-6,4) (-1,4) (5,4) …………(3分)
一共有 9种等可能的结果
其中 a+b>0的有 4种(-1,6)、(-1,4)(5,6)(5,4);
其中 a+b<0的有 4种(-6,-7)、(-6,4)(-1,-7)(5,-7)
4 4
∴P(小聪获胜) = ;P(小明获胜) =
9 9
P(小聪获胜) = P(小明获胜)
∴ 这个游戏公平 …………(6分)
21.解:过点 B作 BE⊥MD于点 E. 则四边形 AMEB是矩形.
呼伦贝尔市、兴安盟初中毕业生学业考试数学答案 第 1 页 (共 7页)
∴BE=AM= 24 3,ME=AB=12
∵AF∥MD
∴∠ACM=
在 Rt△AMC中,∠AMC=90°
∴tan = =2 ∴
∴MC=12 3 …………(3分)
在 Rt△BDE中,∠BED=90° ,∠DBE=90°-30°=60°
∴tan∠DBE= ∴tan60°= = 3 ∴DE= 24 3 × 3 =72
∴CD=DE-CE=DE-(MC-ME)=72-(12 3-12)=84-12 3 ≈84-12×1.7=84-20.4≈64米
答:河流的宽度 CD约为 64米. …………(6分)
四、(本题满分 7分)
22.(1)400 , 176 …………(2分)
(2)C …………(3分)
(3)解:∵n=400-(20+176+144+45)=15
∴扇形统计图中“E”所在扇形的圆心角度数为 15 100% 360 °=13.5°
400
答:扇形统计图中“E”所在扇形的圆心角度数为 13.5°. …………(5分)
(4)解: 45 15×100%=15%
400
15%×2000=300
答:估计该校成绩优秀的学生约有 300名. …………(7分)
五、(本题满分 7分)
23.证明:(1)连接 OC
∵BD⊥CD
∴∠D=90°
∵点 C是 AE的中点
∴AC=CE,
∴∠ABC=∠CBD
∵OB=OC
∴∠OBC=∠OCB
∴∠OCB=∠CBD.
∴OC∥BD
∴∠PCO=∠D =90°
∴OC⊥PD
∵OC是半径
∴PC是⊙O的切线 …………(3分)
(2)证法一:连接 AE交 OC于M
∵PC= 2 2 BO, BO=CO
呼伦贝尔市、兴安盟初中毕业生学业考试数学答案 第 2 页 (共 7页)
∴PC= 2 2 CO
∵PB=10
∴PO=PB-OB=10-OC M
∴在 Rt△PCO中 PC2+OC2=PO2
( 2 2 CO)2+OC2=(10-OC) 2
5
OC= 或 OC=-5(不符合题意,舍去)
2
∵点 C是 AE的中点, OC是半径
∴OC 垂直平分 AE
∵OA=OB
∴OM 是△AEB的中位线
∴BE=2OM …………(5分)
∵AB 是直径
∴∠AEB =∠D =90°, ∴AE∥PD
5
OM OA 1
∴ 2 5 OC OP 10 3
2
1 1 5 5
∴OM= OC =
3 3 2 6
5 5
∴BE= 2 …………(7分)
6 3
证法二:过点 O作 OH⊥BD于点 H,
∴∠DHO =90°,BE=2BH
∵PC= 2 2 BO, BO=CO
∴PC= 2 2 CO
∵PB=10
∴PO=PB-OB=10-OC
∴在 Rt△PCO中 PC2+OC2=PO2 H
( 2 2 CO)2+OC2=(10-OC) 2
5
OC= 或 OC=-5(不符合题意,舍去)
2
∵∠PDB=∠DHO=∠OCD =90°
∴四边形 COHD是矩形
5
∴DH=CO= …………(5分)
2
∵OC∥BD
∴△PCO∽△PDB
PO CO 15 5
∴ ∴
PB BD 2 210 BD
呼伦贝尔市、兴安盟初中毕业生学业考试数学答案 第 3 页 (共 7页)
10
∴BD=
3
10 5 5
∴BH= - =
3 2 6
5 5
∴BE=2 BH=2× = …………(7分)
6 3
六、(本题 9分)
24.解:(1)设每盒豆沙粽的进价为 a元,则每盒肉粽的进价为(a+10)元
2000 2500
a a 10
方程两边乘 a(a 10),得 2000(a 10) 2500a
解得 a=40
检验:当 a=40时,a(a+10)≠0
∴a=40 是原方程的解…
a+10=50
答:每盒肉粽和每盒豆沙粽的进价分别为 50元和 40元. …………(4分)
(2) ①y1=40×80%x=32x(x≥0且 x为整数)
当 0≤x≤25且 x为整数时,y2=40x
当 x>25且 x为整数时,y2=1000+(40x-1000)×70%=28x+300
40x(0 x 25且x为整数)
∴y2= …………(7分)
32x 300(x 25且x为整数)
②当 x>25且 x为整数,
y1= y2 时 32x =28x+300
x=75
由图象可知:购买粽子礼盒少于 75盒,去 A厂家购买划算;
购买粽子礼盒等于 75盒,去 A厂家或 B厂家购买一样划算;
购买粽子礼盒多于 75盒,去 B厂家购买划算. …………(9分)
七、(本题满分 9分)
25. 解:(1)∵四边形 ABCD是正方形,AC是对角线
∴AB=AD,∠BAE=∠DAE=45°
在△ABE和△ADE中
AB AD
BAE DAE
AE AE
∴△ABE≌△ADE (SAS) …………(2分)
(2)△FBG 是等腰三角形,理由如下:
∵△ABE≌△ADE
∴∠ABE=∠ADE
呼伦贝尔市、兴安盟初中毕业生学业考试数学答案 第 4 页 (共 7页)
∵四边形 ABCD是正方形
∴∠DAG=90°
∴∠ADE+∠AGD=90°
∵∠AGD=∠FGB
∴∠ADE+∠FGB=90°
∵FB⊥BE
∴∠EBF=90°
∴∠ABE+∠FBG=90°
∴∠FGB=∠FBG
∴BF=FG
∴△FBG是等腰三角形. …………(5分)
(3)∵BE=BF=2 BF=FG
∴BE= BF=FG=2
又∵FB⊥BE
∴△FBE是等腰直角三角形.
∴∠BEF=∠BAE=45°, BF2+BE2=EF2
∴EF2=22+22=8
∴EF=2 2 ∴GE=2 2 —2
∵∠BEF=∠BAE=45°,∠ABE=∠EBG
∴△ABE∽△EBG
AE EG
∴
AB BE
AE EF FG 2 2 2
∴ 2 1 …………(9分)
AB BE 2
八、(本题满分 13分)
26 1 y x2.解:( )∵抛物线 bx c与 x轴交于点 B(1,0),与 y轴交于点 C(0,3)
1 b c 0
c 3
b 2
解得
c 3
抛物线的解析式为: y x2 2x 3 …………(3分)
2
(2)当 y=0时,0= x 2x 3
解得 x1=-3, x2=1
∴A(-3,0)
设直线 AC的解析式为:y=kx+n(k≠0)
3k n 0 k 1
把 A(-3,0),C(0,3)代入得: 解得
n 3 n 3
呼伦贝尔市、兴安盟初中毕业生学业考试数学答案 第 5 页 (共 7页)
∴直线 AC的解析式为 y=x+3 …………(4分)
设 P(m, m2 2m 3)
∵PE∥x轴
2
∴点 E的纵坐标为 m 2m 3
又∵点 E在直线 AC上
∴ m2 2m 3=x+3 x= m2 2m
∴E( m2 2m , m2 2m 3)
∴PE= m2 2m m = m2 3m
∵PD∥y轴
∴PD= m2 2m 3
∴PD+PE= m2 2m 3 +( m2 3m )= 2m2 5m 3 5 49 = (2 m )2 …………(6分)
4 8
∵-2<0,-3<m<0
5 49
∴当 m= 时,PD+PE有最大值,最大值为
4 8
5 5 2 5 63
当 m= 时, y ( ) 2 ( ) 3
4 4 4 16
5 63
∴点 P的坐标为( , )
4 16
49 5 63
答:PD+PE的最大值为 ,点 P的坐标为( , )
8 4 16 …………(8分)
(3)情况一:当点 N在 y轴上时,P为抛物线的顶点
当x 1时,y ( 1)2 2 ( 1) 3 4
顶点坐标(-1,4)
∵四边形 PMCN为矩形 ∴N与 P纵坐标相同
∴N(0,4)
…………(9分)
当点 N在 x轴负半轴上时,四边形 PMCN 为矩形
过 M 作 y 轴的垂线,垂足为 G, 过 P作 x轴的垂线,垂足为 H,
设 N(t,0),则 ON=-t
∴∠MCN=∠CNP=90°,CM=NP
∴∠MCG+∠OCN=90°
∵∠ONC+∠OCN=90°
∴∠MCG=∠ONC
又∵∠CGM=∠CON=90°
呼伦贝尔市、兴安盟初中毕业生学业考试数学答案 第 6 页 (共 7页)
CG MG
∴△CMG∽△NCO ∴
ON OC
2
∵抛物线对称轴为 x 12 , 点 M在对称轴上,C(0,3) ( 1)
∴MG=1,OC=3
CG 1
∴ ,即CG
1
t
t 3 3
∵∠MCG+∠CMG=90°, ∠ONC+∠PNH=90°
∴∠CMG=∠PNH
1
∴△CMG≌△PNH ∴NH=MG=1, HP=CG= t
3
∴OH=ON+NH=-t+1
1
∴点 P 的坐标为(t-1, t)
3
∵点 P 在抛物线上
1
t (t 1)2 2(t 1) 3
3
t =1 145 , t =1 145 1 145解得 1 2 (舍去) ∴ N( , 0)
6 6 6
1 145
综上所述:符合条件的 N点坐标为:N(0,4) 或 N( , 0)
6 …………(13分)
P N
M G
M
P
H N
呼伦贝尔市、兴安盟初中毕业生学业考试数学答案 第 7 页 (共 7页)
2023 年呼伦贝尔市、兴安盟初中毕业生学业考试
数 学
温馨提示:
1. 本试卷共 6 页,满分 120 分。考试时间 120 分钟。
2. 答卷前务必将自己的姓名、准考证号、座位号填写在答题卡上;选择题答案选出后,请
用 2B 铅笔把答题卡上对应题目的答案标号(ABCD)涂黑,如需改动,请先用橡皮擦拭干净,
再改涂其他答案;非选择题,请用 0.5 毫米的黑色字迹签字笔直接答在答题卡上。在试卷上作
答无效。
3. 请将姓名与准考证号填写在本试卷相应位置上。
4. 考试结束,将试卷、答题卡和草稿纸一并交回。
一、选择题(下列各题的四个选项中只有一个正确. 共 12 小题,每小题 3 分,共 36 分)
1. 5 的倒数是
A 1. B 1. C.5 D. 5
5 5
2.由大小相同的正方体搭成的几何体如图所示,其左视图是
A B C D
3.下列运算正确的是
A. 3 2 3 2 6 B. 3 a2 a6
C 1 1 2 1 b 1. D.
2a a 3a 3ab 3a b 2
4.将一副直角三角板按如图所示的方式摆放,点 C 在 FD 的延长线上,且 AB∥FC,则∠CBD
的度数为
A.10° B.15°
C.20° D.25°
呼伦贝尔市、兴安盟初中毕业生学业考试数学试卷 第 1 页(共 6 页)
{#{QQABAQAUogAgAhBAAQgCQQ3QCkAQkBGAAIoGwEAEMAIBABFABAA=}#}
5.不等式 x 1< 5 的正整数解的个数有
A.3 个 B.4 个 C.5 个 D.6 个
6.下列命题正确的是
A.“经过有交通信号灯的路口,遇到红灯”是必然事件
B.3.14 精确到十分位
C.点( 2 , 3)关于 x轴的对称点坐标是( 2 ,3)
D 2 2.甲、乙两人参加环保知识竞赛,他们的平均成绩相同,方差分别是 S甲=2.25,S乙 =1.81,
则甲成绩比乙的稳定
7.某校举行篮球赛,每场比赛都要分出胜负,每队胜一场得 2 分,负一场得 1 分. 某队在 12
场比赛中得 20 分. 设该队胜 x场,负 y场,则根据题意,列出关于 x、y的二元一次方程组
正确的是
x y 20 x y 12A. B.
x 2y 12 x 2y 20
x y 20 x y 12C. D.
2x y 12
2x y 20
8.若实数 m,n是一元二次方程 x2 2 x 3 =0 的两个根,且 m<n,则点(m,n)所在象限为
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.如图,在菱形 ABCD 中,AB=4,∠A=120°,顺次连接菱形 ABCD 各边中点 E、F、G、H,
则四边形 EFGH 的周长为
A. 4 2 3 B.6 2 3
C. 4 4 3 D.6 4 3
10 k.如图,直线 y ax (b a 0)与双曲线 y (k 0)交于点 A( 2 , 4)和点 B(m , 2),
x
则不等式 0 ax b k 的解集是
x
A. 2
呼伦贝尔市、兴安盟初中毕业生学业考试数学试卷 第 2 页(共 6 页)
{#{QQABAQAUogAgAhBAAQgCQQ3QCkAQkBGAAIoGwEAEMAIBABFABAA=}#}
11.如图,在△ABC 中,∠ABC=90° ,∠BAC=60° , 以点 A 为圆心,以 AB 的长为半径画
弧交 AC 于点 D 1,连接 BD,再分别以点 B,D 为圆心,大于 BD的长为半径画弧,两弧
2
交于点 P,作射线 AP 交 BD 于点 M,交 BC 于点 E,连接 DE,则 S△BDE:S△CDE的值是
A.1:2
B.1: 3
C.2:5
D.3:8
12.将矩形纸板剪掉一个小矩形后剩余部分如图 1 所示,动点 P 从点 A 出发,沿路径 A→B→
C→D→E→F 匀速运动,速度为 1cm/s,点 P 到达终点 F 后停止运动,△APF 的面积
S cm2 S 0 与点 P 运动的时间 t(s)的关系如图 2 所示,根据图象获取了以下的信息:
①AF=5cm;
②a=6;
③点 P 从点 E 运动到点 F 需要 10s;
④矩形纸板裁剪前后周长均为 34cm.
其中正确信息的个数有 图 1 图 2
A.4 个 B.3 个 C.2 个 D.1 个
二、填空题(本题 5 个小题,每小题 3 分,共 15 分)
13.分解因式: x3 4x = .
14.如图,在平面直角坐标系中,点 B 坐标(8,4),连接 OB,将 OB 绕点
O 逆时针旋转 90°,得到 OB’,则点 B’的坐标为 .
15.实数m 2在数轴上对应点的位置如图所示,化简: m 2 .
16.如图,正六边形 ABCDEF 的边长为 2,以点 A 为圆心,AB 为半径画
弧 BF,得到扇形 BAF(阴影部分). 若扇形 BAF 正好是一个圆锥的
侧面展开图,则该圆锥的底面圆的半径是 .
17.观察下列各式:
S 1 1 1 1 1 S 1 1 1 1 1 1 1 11 2 2 , 2 2 2 , S 1 1 ,…1 2 1 2 2 3 2 3 3 32 42 3 4
请利用你所发现的规律,计算: S1 S2 S50 .
呼伦贝尔市、兴安盟初中毕业生学业考试数学试卷 第 3 页(共 6 页)
{#{QQABAQAUogAgAhBAAQgCQQ3QCkAQkBGAAIoGwEAEMAIBABFABAA=}#}
三、解答题(本题 4 个小题,每小题 6 分,共 24 分)
2
18.计算: 8 2 2023 0 1 2cos60 .
2
19 2.先化简,再求值: 2x y x y x y 5x x y ,其中 x 6 1,y 6 1 .
20.如图,A,B 两个带指针的转盘分别被分成三个面积相等的扇形,转盘 A 上的数字分
别是 6, 1,5,转盘 B 上的数字分别是 6, 7,4(两个转盘除表面数字不同外,其他
完全相同). 小聪和小明同时转动 A,B 两个转盘,使之旋转(规定:指针恰好停留在分界
线上,则重新转一次).
(1)转动转盘,转盘 A 指针指向正数的概率是 ;
(2)若同时转动两个转盘,转盘 A 指针所指的数字记为 a,转盘 B 指针所指的数字记为 b,
若 a+b>0,则小聪获胜;若 a+b<0,则小明获胜;请用列表法或树状图法说明这个游
戏是否公平.
21.某数学兴趣小组借助无人机测量一条河流的宽度 CD. 如图所示,一架水平飞行的无人机在
A 处测得河流左岸 C 处的俯角为 ,无人机沿水平线 AF 方向继续飞行 12 米至 B 处,测
得河流右岸 D 处的俯角为 30°,线段 AM= 24 3 米为无人机距地面的铅直高度,点 M,C,
D在同一条直线上,其中 tan =2. 求河流的宽度CD(结果精确到 1米,参考数据: 3 1.7 ).
呼伦贝尔市、兴安盟初中毕业生学业考试数学试卷 第 4 页(共 6 页)
{#{QQABAQAUogAgAhBAAQgCQQ3QCkAQkBGAAIoGwEAEMAIBABFABAA=}#}
四、(本题 7 分)
22.为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学
生成绩进行统计,按成绩分为如下 5 组(满分 100 分),A 组:75≤x<80,B 组:80≤x<85,
C 组:85≤x<90,D 组:90≤x<95,E 组:95≤x≤100,并绘制了如下不完整的统计图表.
请结合统计图表,解答如下问题:
(1)本次调查的样本容量为 ,学生成绩统计表中 m= ;
(2)所抽取学生成绩的中位数落在 组;
(3)求出扇形统计图中“E”所在扇形的圆心角度数;
(4)若成绩在 90 分及以上为优秀,学校共有 2000 名学生,估计该校成绩优秀的学生有多少名?
学生成绩统计表 学生成绩统计图
组别 成绩 x 频数
A 75≤x<80 20
B 80≤x<85 m
C 85≤x<90 144
D 90≤x<95 45
E 95≤x≤100 n
五、(本题 7 分)
23.如图,AB 是⊙O 的直径,E 为⊙O 上的一点,点C 是 AE的中点,连接 BC,过点 C 的直线
垂直于 BE 的延长线于点 D,交 BA 的延长线于点 P.
(1)求证:PC 为⊙O 的切线;
(2)若 PC= 2 2 BO,PB=10,求 BE 的长.
六、(本题 9 分)
24.端午节吃粽子是中华民族的传统习俗. 市场上豆沙粽礼盒的进价比肉粽礼盒的进价每盒便
宜 10 元,某商家用 2500 元购进的肉粽和用 2000 元购进的豆沙粽盒数相同.
(1)求每盒肉粽和每盒豆沙粽的进价;
(2)商家计划只购买豆沙粽礼盒销售,经调查了解到有 A,B 两个厂家可供选择,两个厂
家针对价格相同的豆沙粽礼盒给出了不同的优惠方案:
A 厂家:一律打 8 折出售.
B 厂家:若一次性购买礼盒数量超过 25 盒,超过的部分打 7 折.
该商家计划购买豆沙粽礼盒 x盒,设去 A 厂家购买应付 y1 元,
去 B 厂家购买应付 y 元,其函数图象如图所示:
2
①分别求出 y1 , y2 与 x之间的函数关系;
②若该商家只在一个厂家购买,怎样买划算?
呼伦贝尔市、兴安盟初中毕业生学业考试数学试卷 第 5 页(共 6 页)
{#{QQABAQAUogAgAhBAAQgCQQ3QCkAQkBGAAIoGwEAEMAIBABFABAA=}#}
七、(本题 9 分)
25.已知正方形 ABCD,E 是对角线 AC 上一点.
(1)如图 1,连接 BE,DE. 求证:△ABE≌△ADE;
(2)如图 2,F 是 DE 延长线上一点,DF 交 AB 于点 G,BF⊥BE.
判断△FBG 的形状并说明理由;
3 AE( )在第(2)题的条件下,BE=BF=2. 求 的值.
AB
图 1 图 2
八、(本题 13 分)
26.如图,在平面直角坐标系中,抛物线 y = x2 bx c与 x轴的交点分别为 A 和 B
(1,0)(点A在点 B的左侧),与 y轴交于点C(0,3),点 P 是直线AC 上方抛物线上一动点.
(1)求抛物线的解析式;
(2)如图 1,过点 P 做 x轴平行线交 AC 于点 E,过点 P 做 y 轴平行线交 x 轴于点 D,
求 PE+PD 的最大值及点 P 的坐标;
(3)如图 2,设点 M 为抛物线对称轴上一动点,当点 P,点 M 运动时,在坐标轴上确定点N,
使四边形 PMCN 为矩形,求出所有符合条件的点 N 的坐标.
图 1 图 2 备用图
呼伦贝尔市、兴安盟初中毕业生学业考试数学试卷 第 6 页(共 6 页)
{#{QQABAQAUogAgAhBAAQgCQQ3QCkAQkBGAAIoGwEAEMAIBABFABAA=}#}
2023年呼伦贝尔市、兴安盟初中毕业生学业考试
数学答案及评分标准
一、选择题(每小题 3分,共 36分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A B D B A C D B C B A C
二、填空题(每小题 3分,共 15分)
x(x 2)(x 2) - 2 m 2 50 5013 . 14.( 4, 8) 15. 16. 17.
3 51
三、解答题(每小题 6分,共 24分)
18.解:原式 8 2 1 1 4 2 …………(4分)
2
2 2 2 1 4 1
2 2 2 …………(6分)
19.解:原式=4x2+4xy+y2+x2-y2-5x2+5xy
=9xy …………(4分)
当x 6 1, y 6 1时
原式 (9 6 1)( 6 1) 9(6 1) 45 …………(6分)
1
20.(1) …………(1分)
3
(2)解:列表得:
b a -6 -1 5
6 (-6,6) (-1,6) (5,6)
-7 (-6,-7) (-1,-7) (5,-7)
4 (-6,4) (-1,4) (5,4) …………(3分)
一共有 9种等可能的结果
其中 a+b>0的有 4种(-1,6)、(-1,4)(5,6)(5,4);
其中 a+b<0的有 4种(-6,-7)、(-6,4)(-1,-7)(5,-7)
4 4
∴P(小聪获胜) = ;P(小明获胜) =
9 9
P(小聪获胜) = P(小明获胜)
∴ 这个游戏公平 …………(6分)
21.解:过点 B作 BE⊥MD于点 E. 则四边形 AMEB是矩形.
呼伦贝尔市、兴安盟初中毕业生学业考试数学答案 第 1 页 (共 7页)
∴BE=AM= 24 3,ME=AB=12
∵AF∥MD
∴∠ACM=
在 Rt△AMC中,∠AMC=90°
∴tan = =2 ∴
∴MC=12 3 …………(3分)
在 Rt△BDE中,∠BED=90° ,∠DBE=90°-30°=60°
∴tan∠DBE= ∴tan60°= = 3 ∴DE= 24 3 × 3 =72
∴CD=DE-CE=DE-(MC-ME)=72-(12 3-12)=84-12 3 ≈84-12×1.7=84-20.4≈64米
答:河流的宽度 CD约为 64米. …………(6分)
四、(本题满分 7分)
22.(1)400 , 176 …………(2分)
(2)C …………(3分)
(3)解:∵n=400-(20+176+144+45)=15
∴扇形统计图中“E”所在扇形的圆心角度数为 15 100% 360 °=13.5°
400
答:扇形统计图中“E”所在扇形的圆心角度数为 13.5°. …………(5分)
(4)解: 45 15×100%=15%
400
15%×2000=300
答:估计该校成绩优秀的学生约有 300名. …………(7分)
五、(本题满分 7分)
23.证明:(1)连接 OC
∵BD⊥CD
∴∠D=90°
∵点 C是 AE的中点
∴AC=CE,
∴∠ABC=∠CBD
∵OB=OC
∴∠OBC=∠OCB
∴∠OCB=∠CBD.
∴OC∥BD
∴∠PCO=∠D =90°
∴OC⊥PD
∵OC是半径
∴PC是⊙O的切线 …………(3分)
(2)证法一:连接 AE交 OC于M
∵PC= 2 2 BO, BO=CO
呼伦贝尔市、兴安盟初中毕业生学业考试数学答案 第 2 页 (共 7页)
∴PC= 2 2 CO
∵PB=10
∴PO=PB-OB=10-OC M
∴在 Rt△PCO中 PC2+OC2=PO2
( 2 2 CO)2+OC2=(10-OC) 2
5
OC= 或 OC=-5(不符合题意,舍去)
2
∵点 C是 AE的中点, OC是半径
∴OC 垂直平分 AE
∵OA=OB
∴OM 是△AEB的中位线
∴BE=2OM …………(5分)
∵AB 是直径
∴∠AEB =∠D =90°, ∴AE∥PD
5
OM OA 1
∴ 2 5 OC OP 10 3
2
1 1 5 5
∴OM= OC =
3 3 2 6
5 5
∴BE= 2 …………(7分)
6 3
证法二:过点 O作 OH⊥BD于点 H,
∴∠DHO =90°,BE=2BH
∵PC= 2 2 BO, BO=CO
∴PC= 2 2 CO
∵PB=10
∴PO=PB-OB=10-OC
∴在 Rt△PCO中 PC2+OC2=PO2 H
( 2 2 CO)2+OC2=(10-OC) 2
5
OC= 或 OC=-5(不符合题意,舍去)
2
∵∠PDB=∠DHO=∠OCD =90°
∴四边形 COHD是矩形
5
∴DH=CO= …………(5分)
2
∵OC∥BD
∴△PCO∽△PDB
PO CO 15 5
∴ ∴
PB BD 2 210 BD
呼伦贝尔市、兴安盟初中毕业生学业考试数学答案 第 3 页 (共 7页)
10
∴BD=
3
10 5 5
∴BH= - =
3 2 6
5 5
∴BE=2 BH=2× = …………(7分)
6 3
六、(本题 9分)
24.解:(1)设每盒豆沙粽的进价为 a元,则每盒肉粽的进价为(a+10)元
2000 2500
a a 10
方程两边乘 a(a 10),得 2000(a 10) 2500a
解得 a=40
检验:当 a=40时,a(a+10)≠0
∴a=40 是原方程的解…
a+10=50
答:每盒肉粽和每盒豆沙粽的进价分别为 50元和 40元. …………(4分)
(2) ①y1=40×80%x=32x(x≥0且 x为整数)
当 0≤x≤25且 x为整数时,y2=40x
当 x>25且 x为整数时,y2=1000+(40x-1000)×70%=28x+300
40x(0 x 25且x为整数)
∴y2= …………(7分)
32x 300(x 25且x为整数)
②当 x>25且 x为整数,
y1= y2 时 32x =28x+300
x=75
由图象可知:购买粽子礼盒少于 75盒,去 A厂家购买划算;
购买粽子礼盒等于 75盒,去 A厂家或 B厂家购买一样划算;
购买粽子礼盒多于 75盒,去 B厂家购买划算. …………(9分)
七、(本题满分 9分)
25. 解:(1)∵四边形 ABCD是正方形,AC是对角线
∴AB=AD,∠BAE=∠DAE=45°
在△ABE和△ADE中
AB AD
BAE DAE
AE AE
∴△ABE≌△ADE (SAS) …………(2分)
(2)△FBG 是等腰三角形,理由如下:
∵△ABE≌△ADE
∴∠ABE=∠ADE
呼伦贝尔市、兴安盟初中毕业生学业考试数学答案 第 4 页 (共 7页)
∵四边形 ABCD是正方形
∴∠DAG=90°
∴∠ADE+∠AGD=90°
∵∠AGD=∠FGB
∴∠ADE+∠FGB=90°
∵FB⊥BE
∴∠EBF=90°
∴∠ABE+∠FBG=90°
∴∠FGB=∠FBG
∴BF=FG
∴△FBG是等腰三角形. …………(5分)
(3)∵BE=BF=2 BF=FG
∴BE= BF=FG=2
又∵FB⊥BE
∴△FBE是等腰直角三角形.
∴∠BEF=∠BAE=45°, BF2+BE2=EF2
∴EF2=22+22=8
∴EF=2 2 ∴GE=2 2 —2
∵∠BEF=∠BAE=45°,∠ABE=∠EBG
∴△ABE∽△EBG
AE EG
∴
AB BE
AE EF FG 2 2 2
∴ 2 1 …………(9分)
AB BE 2
八、(本题满分 13分)
26 1 y x2.解:( )∵抛物线 bx c与 x轴交于点 B(1,0),与 y轴交于点 C(0,3)
1 b c 0
c 3
b 2
解得
c 3
抛物线的解析式为: y x2 2x 3 …………(3分)
2
(2)当 y=0时,0= x 2x 3
解得 x1=-3, x2=1
∴A(-3,0)
设直线 AC的解析式为:y=kx+n(k≠0)
3k n 0 k 1
把 A(-3,0),C(0,3)代入得: 解得
n 3 n 3
呼伦贝尔市、兴安盟初中毕业生学业考试数学答案 第 5 页 (共 7页)
∴直线 AC的解析式为 y=x+3 …………(4分)
设 P(m, m2 2m 3)
∵PE∥x轴
2
∴点 E的纵坐标为 m 2m 3
又∵点 E在直线 AC上
∴ m2 2m 3=x+3 x= m2 2m
∴E( m2 2m , m2 2m 3)
∴PE= m2 2m m = m2 3m
∵PD∥y轴
∴PD= m2 2m 3
∴PD+PE= m2 2m 3 +( m2 3m )= 2m2 5m 3 5 49 = (2 m )2 …………(6分)
4 8
∵-2<0,-3<m<0
5 49
∴当 m= 时,PD+PE有最大值,最大值为
4 8
5 5 2 5 63
当 m= 时, y ( ) 2 ( ) 3
4 4 4 16
5 63
∴点 P的坐标为( , )
4 16
49 5 63
答:PD+PE的最大值为 ,点 P的坐标为( , )
8 4 16 …………(8分)
(3)情况一:当点 N在 y轴上时,P为抛物线的顶点
当x 1时,y ( 1)2 2 ( 1) 3 4
顶点坐标(-1,4)
∵四边形 PMCN为矩形 ∴N与 P纵坐标相同
∴N(0,4)
…………(9分)
当点 N在 x轴负半轴上时,四边形 PMCN 为矩形
过 M 作 y 轴的垂线,垂足为 G, 过 P作 x轴的垂线,垂足为 H,
设 N(t,0),则 ON=-t
∴∠MCN=∠CNP=90°,CM=NP
∴∠MCG+∠OCN=90°
∵∠ONC+∠OCN=90°
∴∠MCG=∠ONC
又∵∠CGM=∠CON=90°
呼伦贝尔市、兴安盟初中毕业生学业考试数学答案 第 6 页 (共 7页)
CG MG
∴△CMG∽△NCO ∴
ON OC
2
∵抛物线对称轴为 x 12 , 点 M在对称轴上,C(0,3) ( 1)
∴MG=1,OC=3
CG 1
∴ ,即CG
1
t
t 3 3
∵∠MCG+∠CMG=90°, ∠ONC+∠PNH=90°
∴∠CMG=∠PNH
1
∴△CMG≌△PNH ∴NH=MG=1, HP=CG= t
3
∴OH=ON+NH=-t+1
1
∴点 P 的坐标为(t-1, t)
3
∵点 P 在抛物线上
1
t (t 1)2 2(t 1) 3
3
t =1 145 , t =1 145 1 145解得 1 2 (舍去) ∴ N( , 0)
6 6 6
1 145
综上所述:符合条件的 N点坐标为:N(0,4) 或 N( , 0)
6 …………(13分)
P N
M G
M
P
H N
呼伦贝尔市、兴安盟初中毕业生学业考试数学答案 第 7 页 (共 7页)
同课章节目录
