青岛版2014-2015学年第一学期第二次质量检测九年级数学试题
文档属性
| 名称 | 青岛版2014-2015学年第一学期第二次质量检测九年级数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 186.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-29 15:51:16 | ||
图片预览



文档简介
2014-2015学年第一学期第二次质量检测九年级数学试题
一.选择题(共15小题)
1.如果两个相似多边形面积的比为1:5,则它们的相似比为( )
A.1:25 B. 1:5 C. 1:2.5 D. 1:
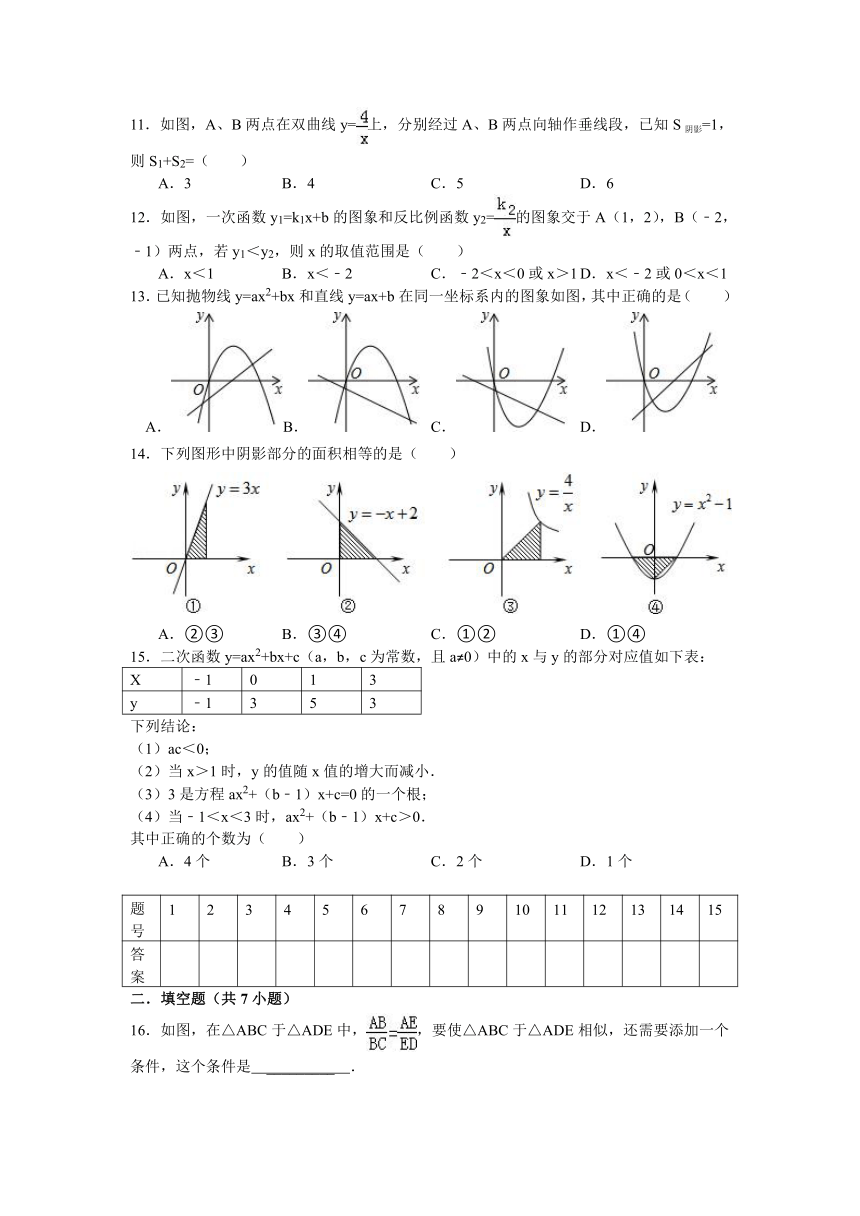
2.如图,在第一象限内,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的,那么点B′的坐标是( )
A.(3,2) B. (12,8) C. (2,3) D. (8,12)
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(2) (3) (4) (5)
3.如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
A. B. C. D.
4.如图,在⊙O中,OD⊥BC,∠BOD=60°,则∠CAD的度数等于( )
A.15° B. 20° C. 25° D. 30°
5.如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠B=25°,则∠C的大小等于( )
A.20° B. 25° C. 40° D. 50°
6.在圆心角为120°的扇形AOB中,半径OA=6cm,则扇形OAB的面积是( )
A.6πcm2 B. 8πcm2 C. 12πcm2 D. 24πcm2
7.如图,正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( )
A.πa B. 2πa C. D. 3a
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(7) (11) (12)
8.正六边形的边长等于2,则这个正六边形的面积等于( )
A.4 B. 6 C. 7 D. 8
9.用配方法解一元二次方程x2+4x﹣5=0,此方程可变形为( )
A.(x+2)2=9 B. (x﹣2)2=9 C. (x+2)2=1 D. (x﹣2)2=1
10.若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )
A.k> B. k≥ C. k>且k≠1 D. k≥且k≠1
11.如图,A、B两点在双曲线y=上,分别经过A、B两点向轴作垂线段,已知S阴影=1,则S1+S2=( )
A.3 B. 4 C. 5 D. 6
12.如图,一次函数y1=k1x+b的图象和反比例函数y2=的图象交于A(1,2),B(﹣2,﹣1)两点,若y1<y2,则x的取值范围是( )
A.x<1 B. x<﹣2 C. ﹣2<x<0或x>1 D. x<﹣2或0<x<1
13.已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图,其中正确的是( )
A. ( http: / / www.21cnjy.com )B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
14.下列图形中阴影部分的面积相等的是( )
( http: / / www.21cnjy.com )
A.②③ B. ③④ C. ①② D. ①④
15.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
X ﹣1 0 1 3
y ﹣1 3 5 3
下列结论:
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小.
(3)3是方程ax2+(b﹣1)x+c=0的一个根;
(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为( )
A.4个 B. 3个 C. 2个 D. 1个
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
答案
二.填空题(共7小题)
16.如图,在△ABC于△ADE中,,要使△ABC于△ADE相似,还需要添加一个条件,这个条件是 _________ .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(16) (17) (18) (20)
17.如图,方格纸中的每个小方格都是边长 ( http: / / www.21cnjy.com )为1个单位长度的正方形,每个小正方形的顶点叫格点.△ABC的顶点都在方格的格点上,则cosA= _________ .
18.如图,在⊙O中,半径OA垂直弦于点D.若∠ACB=33°,则∠OBC的大小为 _________ 度.
19.若关于x的方程x2+(k﹣2)x+k2=0的两根互为倒数,则k= _________ .
20.一件商品的原价是100元,经过两次提 ( http: / / www.21cnjy.com )价后的价格为121元,如果每次提价的百分率都是x.根据题意,可列出方程为: _________ .
21.如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数的图象经过点C,则k的值为_______ .
22.将抛物线y=(x﹣3)2+1先向上平移2个单位,再向左平移1个单位后,得到的抛物线解析式为 _________ .
三.解答题(共7小题)
23.如图,点D在等边△ABC的BC边上,△ADE为等边三角形,DE与AC交于点F.
(1)证明:△ABD∽△DCF;
(2)除了△ABD∽△DCF外,请写出图中其他所有的相似三角形.
( http: / / www.21cnjy.com )
24.如图,AB、CD为两个建筑物,建筑物 ( http: / / www.21cnjy.com )AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
( http: / / www.21cnjy.com )
25.如图,AB是⊙O的直径,点F,C是⊙O上两点,且==,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2,求⊙O的半径.
( http: / / www.21cnjy.com )
26.天山旅行社为吸引游客组团去具有喀斯特地貌特征的黄果树风景区旅游,推出了如下收费标准(如图所示):
( http: / / www.21cnjy.com )
某单位组织员工去具有喀斯特 ( http: / / www.21cnjy.com )地貌特征的黄果树风景区旅游,共支付给旅行社旅游费用27000元,请问该单位这次共有多少名员工去具有喀斯特地貌特征的黄果树风景区旅游?
27.为了预防流感,学校对教室进行“药 ( http: / / www.21cnjy.com )熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(min)成正比,燃烧后,y与x成反比(如图),现测得药物10min燃烧完,此时,教室内每立方米空气含药量为16mg.已知每立方米空气中含药量低于4mg时对人体无害,那么从消毒开始经多长时间后学生才能进教室?
( http: / / www.21cnjy.com )
28.某经销商销售一种产品,这种产 ( http: / / www.21cnjy.com )品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得150元的销售利润,销售价应定为多少?
( http: / / www.21cnjy.com )
29.二次函数y=ax2+bx+c的图象经过点(﹣1,4),且与直线y=﹣x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).
(1)求二次函数的表达式;
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)在(2)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标.
( http: / / www.21cnjy.com )
参考答案
一.选择题(共15小题)
1. D.2. A.3. D.4.D.5.C.6. C.7. A.8. B.9. A.10. C.
11. D.12. D.13. D.14. A.15. B.
二.填空题(共7小题)
16. ∠B=∠E .17. .18. 24 19. ﹣1 .
20. 100(1+x)2=121 .21. ﹣6 .
22. y═(x﹣2)2+3 .
三.解答题(共7小题)
23.(1)证明:∵△ABC,△ADE为等边三角形,∴∠B=∠C=∠3=60°,
∴∠1+∠2=∠DFC+∠2,∴∠1=∠DFC,∴△ABD∽△DCF;
(2)解:∵∠C=∠E,∠AFE=∠DFC,∴△AEF∽△DCF,∴△ABD∽△AEF,
故除了△ABD∽△DCF外,图中相似三角形还有:△AEF∽△DCF,△ABD∽△AEF,△ABC∽△ADE,△ADF∽△ACD.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(23) (24) (25)
24. 解:(1)根据题意得:BD∥AE,∴∠ADB=∠EAD=45°,
∵∠ABD=90°,∴∠BAD=∠ADB=45°,∴BD=AB=60,
∴两建筑物底部之间水平距离BD的长度为60米;
(2)延长AE、DC交于点F,根据题意得四边形ABDF为正方形,∴AF=BD=DF=60,
在Rt△AFC中,∠FAC=30°,∴CF=AF tan∠FAC=60×=20,
又∵FD=60,∴CD=60﹣20,
∴建筑物CD的高度为(60﹣20)米.
25.(1)证明:连结OC,如图,∵=,∴∠FAC=∠BAC,
∵OA=OC,∴∠OAC=∠OCA,∴∠FAC=∠OCA,∴OC∥AF,
∵CD⊥AF,∴OC⊥CD,∴CD是⊙O的切线;
(2)解:连结BC,如图,∵AB为直径,∴∠ACB=90°,
∵==,∴∠BOC=×180°=60°,∴∠BAC=30°,∴∠DAC=30°,
在Rt△ADC中,CD=2,∴AC=2CD=4,在Rt△ACB中,BC=AC=×4=4,
∴AB=2BC=8,
∴⊙O的半径为4.
26.解:设该单位去具有喀斯特地貌特征的黄果树旅游人数为x人,则人均费用为1000﹣20(x﹣25)元
由题意得 x[1000﹣20(x﹣25)]=27000
整理得x2﹣75x+1350=0,
解得x1=45,x2=30.
当x=45时,人均旅游费用为1000﹣20(x﹣25)=600<700,不符合题意,应舍去.
当x=30时,人均旅游费用为1000﹣20(x﹣25)=900>700,符合题意.
答:该单位这次共有30名员工去具有喀斯特地貌特征的黄果树风景区旅游.
27.解:设燃烧后的函数解析式为y=,∵图象经过点(10,16),∴k=160,
∴y=.由,得x=40∴从消毒开始要经过40分钟后学生才能进教室.
28.解:(1)设y与x之间的函数关系式y=kx+b,把(10,40),(18,24)代入得
,解得,
∴y与x之间的函数关系式y=﹣2x+60(10≤x≤18);
(2)W=(x﹣10)(﹣2x+60)=﹣2x2+80x﹣600,
对称轴x=20,在对称轴的左侧y随着x的增大而增大,
∵10≤x≤18,
∴当x=18时,W最大,最大为192.
即当销售价为18元时,每天的销售利润最大,最大利润是192元.
(3)由150=﹣2x2+80x﹣600,
解得x1=15,x2=25(不合题意,舍去)
答:该经销商想要每天获得150元的销售利润,销售价应定为15元.
29.解:(1)由直线y=﹣x+1可知A(0,1),B(﹣3,),又点(﹣1,4)经过二次函数,
根据题意得: ( http: / / www.21cnjy.com ),解得:,
则二次函数的解析式是:y=﹣﹣x+1;
(2)设N(x,﹣x2﹣x+1),
则M(x,﹣x+1),P(x,0).
∴MN=PN﹣PM=﹣x2﹣x+1﹣(﹣x+1)=﹣x2﹣x=﹣(x+)2+,
则当x=﹣时,MN的最大值为;
(3)连接MN、BN、BM与NC互相垂直平分,
即四边形BCMN是菱形,
由于BC∥MN,
即MN=BC,且BC=MC,
即﹣x2﹣x=,
且(﹣x+1)2+(x+3)2=,
解得:x=﹣1或x=﹣2(不合题意舍去),
故当N(﹣1,4)时,BM和NC互相垂直平分.
( http: / / www.21cnjy.com )
一.选择题(共15小题)
1.如果两个相似多边形面积的比为1:5,则它们的相似比为( )
A.1:25 B. 1:5 C. 1:2.5 D. 1:
2.如图,在第一象限内,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的,那么点B′的坐标是( )
A.(3,2) B. (12,8) C. (2,3) D. (8,12)
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(2) (3) (4) (5)
3.如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
A. B. C. D.
4.如图,在⊙O中,OD⊥BC,∠BOD=60°,则∠CAD的度数等于( )
A.15° B. 20° C. 25° D. 30°
5.如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠B=25°,则∠C的大小等于( )
A.20° B. 25° C. 40° D. 50°
6.在圆心角为120°的扇形AOB中,半径OA=6cm,则扇形OAB的面积是( )
A.6πcm2 B. 8πcm2 C. 12πcm2 D. 24πcm2
7.如图,正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( )
A.πa B. 2πa C. D. 3a
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(7) (11) (12)
8.正六边形的边长等于2,则这个正六边形的面积等于( )
A.4 B. 6 C. 7 D. 8
9.用配方法解一元二次方程x2+4x﹣5=0,此方程可变形为( )
A.(x+2)2=9 B. (x﹣2)2=9 C. (x+2)2=1 D. (x﹣2)2=1
10.若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )
A.k> B. k≥ C. k>且k≠1 D. k≥且k≠1
11.如图,A、B两点在双曲线y=上,分别经过A、B两点向轴作垂线段,已知S阴影=1,则S1+S2=( )
A.3 B. 4 C. 5 D. 6
12.如图,一次函数y1=k1x+b的图象和反比例函数y2=的图象交于A(1,2),B(﹣2,﹣1)两点,若y1<y2,则x的取值范围是( )
A.x<1 B. x<﹣2 C. ﹣2<x<0或x>1 D. x<﹣2或0<x<1
13.已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图,其中正确的是( )
A. ( http: / / www.21cnjy.com )B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
14.下列图形中阴影部分的面积相等的是( )
( http: / / www.21cnjy.com )
A.②③ B. ③④ C. ①② D. ①④
15.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
X ﹣1 0 1 3
y ﹣1 3 5 3
下列结论:
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小.
(3)3是方程ax2+(b﹣1)x+c=0的一个根;
(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为( )
A.4个 B. 3个 C. 2个 D. 1个
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
答案
二.填空题(共7小题)
16.如图,在△ABC于△ADE中,,要使△ABC于△ADE相似,还需要添加一个条件,这个条件是 _________ .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(16) (17) (18) (20)
17.如图,方格纸中的每个小方格都是边长 ( http: / / www.21cnjy.com )为1个单位长度的正方形,每个小正方形的顶点叫格点.△ABC的顶点都在方格的格点上,则cosA= _________ .
18.如图,在⊙O中,半径OA垂直弦于点D.若∠ACB=33°,则∠OBC的大小为 _________ 度.
19.若关于x的方程x2+(k﹣2)x+k2=0的两根互为倒数,则k= _________ .
20.一件商品的原价是100元,经过两次提 ( http: / / www.21cnjy.com )价后的价格为121元,如果每次提价的百分率都是x.根据题意,可列出方程为: _________ .
21.如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数的图象经过点C,则k的值为_______ .
22.将抛物线y=(x﹣3)2+1先向上平移2个单位,再向左平移1个单位后,得到的抛物线解析式为 _________ .
三.解答题(共7小题)
23.如图,点D在等边△ABC的BC边上,△ADE为等边三角形,DE与AC交于点F.
(1)证明:△ABD∽△DCF;
(2)除了△ABD∽△DCF外,请写出图中其他所有的相似三角形.
( http: / / www.21cnjy.com )
24.如图,AB、CD为两个建筑物,建筑物 ( http: / / www.21cnjy.com )AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
( http: / / www.21cnjy.com )
25.如图,AB是⊙O的直径,点F,C是⊙O上两点,且==,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2,求⊙O的半径.
( http: / / www.21cnjy.com )
26.天山旅行社为吸引游客组团去具有喀斯特地貌特征的黄果树风景区旅游,推出了如下收费标准(如图所示):
( http: / / www.21cnjy.com )
某单位组织员工去具有喀斯特 ( http: / / www.21cnjy.com )地貌特征的黄果树风景区旅游,共支付给旅行社旅游费用27000元,请问该单位这次共有多少名员工去具有喀斯特地貌特征的黄果树风景区旅游?
27.为了预防流感,学校对教室进行“药 ( http: / / www.21cnjy.com )熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(min)成正比,燃烧后,y与x成反比(如图),现测得药物10min燃烧完,此时,教室内每立方米空气含药量为16mg.已知每立方米空气中含药量低于4mg时对人体无害,那么从消毒开始经多长时间后学生才能进教室?
( http: / / www.21cnjy.com )
28.某经销商销售一种产品,这种产 ( http: / / www.21cnjy.com )品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得150元的销售利润,销售价应定为多少?
( http: / / www.21cnjy.com )
29.二次函数y=ax2+bx+c的图象经过点(﹣1,4),且与直线y=﹣x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).
(1)求二次函数的表达式;
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)在(2)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标.
( http: / / www.21cnjy.com )
参考答案
一.选择题(共15小题)
1. D.2. A.3. D.4.D.5.C.6. C.7. A.8. B.9. A.10. C.
11. D.12. D.13. D.14. A.15. B.
二.填空题(共7小题)
16. ∠B=∠E .17. .18. 24 19. ﹣1 .
20. 100(1+x)2=121 .21. ﹣6 .
22. y═(x﹣2)2+3 .
三.解答题(共7小题)
23.(1)证明:∵△ABC,△ADE为等边三角形,∴∠B=∠C=∠3=60°,
∴∠1+∠2=∠DFC+∠2,∴∠1=∠DFC,∴△ABD∽△DCF;
(2)解:∵∠C=∠E,∠AFE=∠DFC,∴△AEF∽△DCF,∴△ABD∽△AEF,
故除了△ABD∽△DCF外,图中相似三角形还有:△AEF∽△DCF,△ABD∽△AEF,△ABC∽△ADE,△ADF∽△ACD.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(23) (24) (25)
24. 解:(1)根据题意得:BD∥AE,∴∠ADB=∠EAD=45°,
∵∠ABD=90°,∴∠BAD=∠ADB=45°,∴BD=AB=60,
∴两建筑物底部之间水平距离BD的长度为60米;
(2)延长AE、DC交于点F,根据题意得四边形ABDF为正方形,∴AF=BD=DF=60,
在Rt△AFC中,∠FAC=30°,∴CF=AF tan∠FAC=60×=20,
又∵FD=60,∴CD=60﹣20,
∴建筑物CD的高度为(60﹣20)米.
25.(1)证明:连结OC,如图,∵=,∴∠FAC=∠BAC,
∵OA=OC,∴∠OAC=∠OCA,∴∠FAC=∠OCA,∴OC∥AF,
∵CD⊥AF,∴OC⊥CD,∴CD是⊙O的切线;
(2)解:连结BC,如图,∵AB为直径,∴∠ACB=90°,
∵==,∴∠BOC=×180°=60°,∴∠BAC=30°,∴∠DAC=30°,
在Rt△ADC中,CD=2,∴AC=2CD=4,在Rt△ACB中,BC=AC=×4=4,
∴AB=2BC=8,
∴⊙O的半径为4.
26.解:设该单位去具有喀斯特地貌特征的黄果树旅游人数为x人,则人均费用为1000﹣20(x﹣25)元
由题意得 x[1000﹣20(x﹣25)]=27000
整理得x2﹣75x+1350=0,
解得x1=45,x2=30.
当x=45时,人均旅游费用为1000﹣20(x﹣25)=600<700,不符合题意,应舍去.
当x=30时,人均旅游费用为1000﹣20(x﹣25)=900>700,符合题意.
答:该单位这次共有30名员工去具有喀斯特地貌特征的黄果树风景区旅游.
27.解:设燃烧后的函数解析式为y=,∵图象经过点(10,16),∴k=160,
∴y=.由,得x=40∴从消毒开始要经过40分钟后学生才能进教室.
28.解:(1)设y与x之间的函数关系式y=kx+b,把(10,40),(18,24)代入得
,解得,
∴y与x之间的函数关系式y=﹣2x+60(10≤x≤18);
(2)W=(x﹣10)(﹣2x+60)=﹣2x2+80x﹣600,
对称轴x=20,在对称轴的左侧y随着x的增大而增大,
∵10≤x≤18,
∴当x=18时,W最大,最大为192.
即当销售价为18元时,每天的销售利润最大,最大利润是192元.
(3)由150=﹣2x2+80x﹣600,
解得x1=15,x2=25(不合题意,舍去)
答:该经销商想要每天获得150元的销售利润,销售价应定为15元.
29.解:(1)由直线y=﹣x+1可知A(0,1),B(﹣3,),又点(﹣1,4)经过二次函数,
根据题意得: ( http: / / www.21cnjy.com ),解得:,
则二次函数的解析式是:y=﹣﹣x+1;
(2)设N(x,﹣x2﹣x+1),
则M(x,﹣x+1),P(x,0).
∴MN=PN﹣PM=﹣x2﹣x+1﹣(﹣x+1)=﹣x2﹣x=﹣(x+)2+,
则当x=﹣时,MN的最大值为;
(3)连接MN、BN、BM与NC互相垂直平分,
即四边形BCMN是菱形,
由于BC∥MN,
即MN=BC,且BC=MC,
即﹣x2﹣x=,
且(﹣x+1)2+(x+3)2=,
解得:x=﹣1或x=﹣2(不合题意舍去),
故当N(﹣1,4)时,BM和NC互相垂直平分.
( http: / / www.21cnjy.com )
同课章节目录
