北师大版数学八年级上册 5.7用二元一次方程组确定一次函数表达式 教学设计
文档属性
| 名称 | 北师大版数学八年级上册 5.7用二元一次方程组确定一次函数表达式 教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 182.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 14:56:03 | ||
图片预览



文档简介
第5章 二元一次方程
7.用二元一次方程组确定一次函数表达式
1、教学目标
知识与技能
1.了解二元一次方程与一次函数的关系;
2.了解待定系数法以及待定系数法的一般步骤;
3.会用二元一次方程组确定一次函数的表达式。
过程与方法
让学生体会一次函数与二元一次方程组的联系,感受“数形结合”的作用。
情感、态度与价值观
通过学生小组讨论,培养学生思考、团结合作的精神。
2、教学重难点
重点:利用二元一次方程组确定一次函数的表达式。
难点:应用二元一次方程组和函数的联系解决实际问题。
三、温故知新
1.确定正比例函数的表达式需要几个条件?
确定一次函数的表达式需要几个条件?
2.点A在正比例函数的图象上,这个正比例函数的表达式为_________。
3.已知一次函数经点和,求一次函数的解析式为__________。
四、学习过程
(一)探究活动
已知一次函数经过点和,求一次函数的解析式为_________。
解:设一次函数解析式为,
将 和分别代入得:,
解得:
所以一次函数的解析式为 。
总结:确定一次函数表达式的步骤是什么呢?
1.设:设一次函数表达式为 ;
2.代:将点的坐标代入中,列出关于k和b的方程或方程组;
3.解:解方程或方程组,求出k和b;
4.写:将所求得的k和b值代回表达式中,从而写出表达式。
这种求函数解析式的方法叫做待定系数法。
(二)例题解析
某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费y(元)是行李质量 x(kg)的一次函数.现知李明带了60 kg的行李,交了行李费5元;张华带了90 kg的行李,交了行李费10元。
(1)写出y与x之间的函数表达式;
(2)旅客最多可免费携带多少千克的行李?
解:(1)设一次函数解析式为 ,
由题意得:,解得:
所以y 与 x 之间的关系式为 。
(2)当y=0时,,解得:
答:旅客最多可免费携带30千克的行李。
(三)学以致用
在弹性限度内,弹簧的长度y(cm)是所挂物体质量 x(kg)的一次函数。当所挂物体的质量为1kg时,弹簧长15厘米;当所挂物体的质量为3 kg时,弹簧长16 cm。写出 y 与 x 之间的关系式,并求出所挂物体的质量为4 kg时弹簧的长度。
解:(1)设一次函数解析式为 ,
由题意得:,解得:
所以y 与 x 之间的关系式为 。
(2)当x=4时,y=0.5×4+14.5=16.5(cm)
答:所挂物体的质量为4 kg时弹簧的长度为16.5cm。
(四)拓展延伸
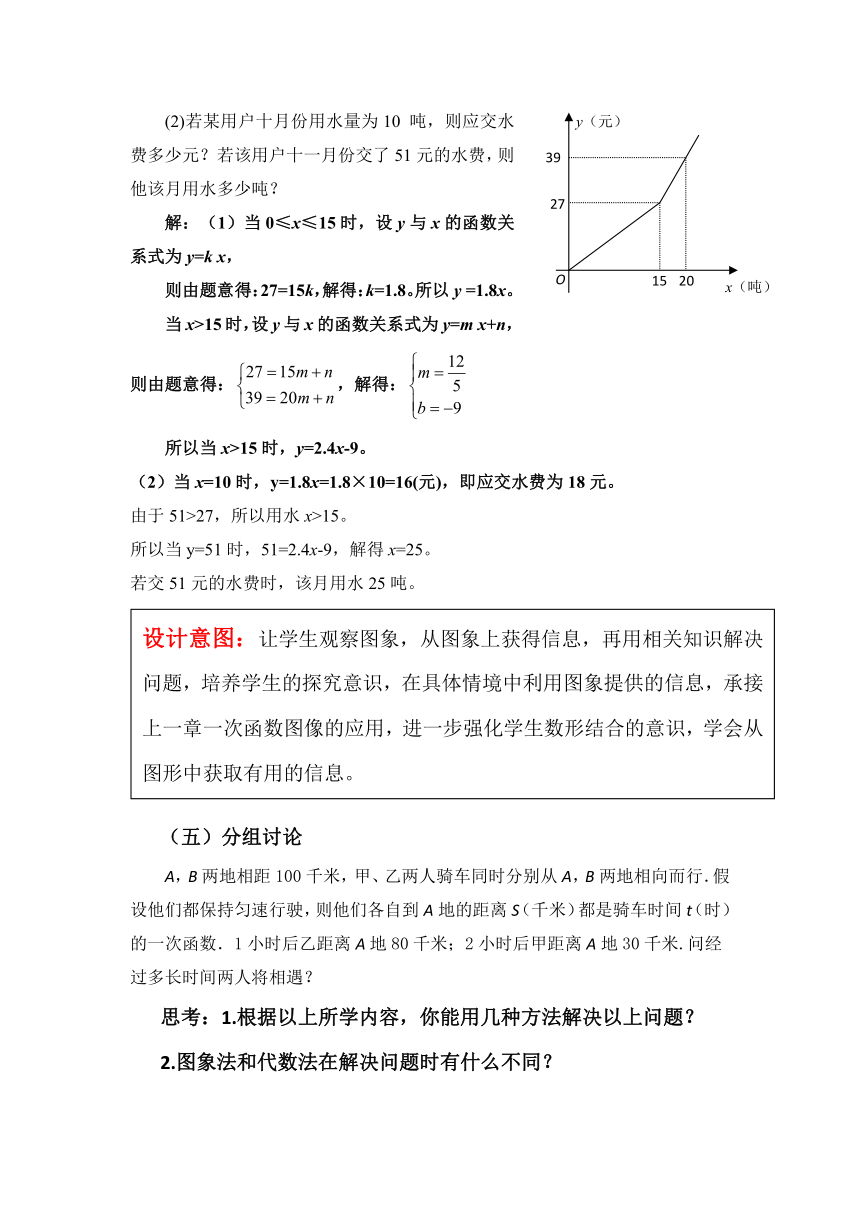
某市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若某户居民应交水费 y(元)与用水量x(吨)的函数关系如图所示。
(1)分别写出当0≤x≤15和x>15时,y与x的函数关系式;
(2)若某用户十月份用水量为10 吨,则应交水费多少元?若该用户十一月份交了51元的水费,则他该月用水多少吨?
解:(1)当0≤x≤15时,设y与x的函数关系式为y=k x,
则由题意得:27=15k,解得:k=1.8。所以y =1.8x。
当x>15时,设y与x的函数关系式为y=m x+n,则由题意得:,解得:
所以当x>15时,y=2.4x-9。
(2)当x=10时,y=1.8x=1.8×10=16(元),即应交水费为18元。
由于51>27,所以用水x>15。
所以当y=51时,51=2.4x-9,解得x=25。
若交51元的水费时,该月用水25吨。
(五)分组讨论
A,B两地相距100千米,甲、乙两人骑车同时分别从A,B两地相向而行.假设他们都保持匀速行驶,则他们各自到A地的距离S(千米)都是骑车时间t(时)的一次函数.1小时后乙距离A地80千米;2小时后甲距离A地30千米.问经过多长时间两人将相遇?
思考:1.根据以上所学内容,你能用几种方法解决以上问题?
2.图象法和代数法在解决问题时有什么不同?
五、课堂小结
1.函数与方程之间的关系;
2.掌握利用二元一次方程组求一次函数表达式的步骤:待定系数法
设 代 解 写
六.课后练习
1. 一次函数y=k x+b的图象与x轴、y轴的交点坐标分别是(2,0)和(0,-1),则这个函数的表达式子为 ( )
A. B.
C. D.
解:设,
将(2,0)和(0,-1)代入得:
解得:
所以函数的表达式为。
2. 已知函数y=2x+b的图象经过点(a,7)和(-2,a),则这个函数的表达式为 ( )
A. B.
C. D.
解:由于y=2x+b,
所以将(a,7)和(-2,a)分别代入得:
解得:。
所以y=2x+5。
3. 求出图中的两条直线 l1和l2的函数表达式。
解:设l1:y1=k1x+b1
把(0,1)和(1,3)分别代入得:
解得:.
所以l1:y1=2x+1.
设l1:y2=k2x+b2
把(4,0)和(0,4)分别代入得:
解得:
所以l2:y2=-x+4。
4.某饮料厂生产一种饮料,经测算,用一吨水生产的饮料利润(元)是一吨水的价格(元)的一次函数,根据下表提供的数据,求与的函数关系式;当水价为每吨10元时,一吨水生产出的饮料的利润是多少?
一吨水的价格/元 4 6
用一吨水生产的饮料所获利润/元 200 198
解:(1)设一次函数解析式为 ,
由题意得:
解得:。
所以y 与 x 之间的关系式为。
(2)当x=10时,y=-10+204=194(元)
所以一吨水生产出的饮料的利润是194元。
5.小明在暑期社会实践活动中,以每千克0.8元的价格从批发市场购进若干千克西瓜到市场上去销售,在销售了40千克西瓜之后,余下的以每千克降价0.4元全部售完。销售金额与售出西瓜的千克数之间的关系如图所示。
请你根据图象提供的信息完成以下问题:的函数关系如图所示。
(1)求降价前销售金额 y(元)与售出西瓜x(千克)之间的函数关系式;
(2)小明从批发市场共购进多少千克西瓜?
(3)小明这次卖瓜赚了多少钱?
解:(1)设函数关系式为,由题意得:,解得:。所以降价前销售金额 y(元)与售出西瓜x(千克)之间的函数关系式。
(2)(kg);(kg)。
所以小明从批发市场共购进70千克西瓜
(3)
所以小明这次卖瓜赚了20元。
七.教学反思
根据我对教材的理解,上课后的感受,进行教学反思。
1.在学习一次函数与一元一次方程、一元一次不等式之间的关系后进行一次函数与二元一次方程组关系的学习,学生对于解二元一次方程组比较有信心。
2.学生对函数与方程、不等式之间的关系有一定的认识,能通过函数图象理解它们之间的关系,但是课堂上利用函数图像理解一次函数与方程组之间的关系这一内容时间稍微少了一些。
3.班级学生喜欢解计算题,但是对应用题有一种惧怕心理,因此本节课重点是从简单的题出发,让学生了解什么是待定系数法,然后进一步层层递进,设置实际情境问题。
4.本节内容对学困生而言比较困难,这也是这节课的失败之处。此外,在教学的过程中,应对学困生进行及时的辅导。同时也需要注重学生的解题过程,引导学生发现解决问题的渠道。
1.设
4.写
3.解
2.代
设计意图:让学生分析题意,思考如何解决,通过简单的题目,让学生交流讨论总结如何确定一次函数的表达式。
设计意图:通过实际问题情境,注重引导学生分析问题,从实际情境中寻找确定函数表达式的条件,进一步加强函数与方程的联系,用待定系数法确定一次函数的表达式,突破本课重点,培养学生的逻辑思维能力。
设计意图:通过练习进行强化,目的在于加强学生“利用二元一次方程组确定一次函数解析式”。
x(吨)
y(元)
15
20
39
27
O
设计意图:让学生观察图象,从图象上获得信息,再用相关知识解决问题,培养学生的探究意识,在具体情境中利用图象提供的信息,承接上一章一次函数图像的应用,进一步强化学生数形结合的意识,学会从图形中获取有用的信息。
设计意图:通过实际问题情境,让学生在多种方法解决问题,思考和比较体会图象法和代数法各自的特点,理解知识之间的广泛联系。
设计意图:让学生归纳和总结本节所学的内容,进行总结和自我反思。
o
y
x
1
2
3
4
1
2
3
4
方法提示:求一次函数的表达式一般用待定系数法,这需要两个条件,如直线上的两个点的左边、两对函数值等,这就需要学生认真分析所给的条件,找出相应条件。让学生在学习中进一步体会二元一次方程组与一次函数之间的关系。
7.用二元一次方程组确定一次函数表达式
1、教学目标
知识与技能
1.了解二元一次方程与一次函数的关系;
2.了解待定系数法以及待定系数法的一般步骤;
3.会用二元一次方程组确定一次函数的表达式。
过程与方法
让学生体会一次函数与二元一次方程组的联系,感受“数形结合”的作用。
情感、态度与价值观
通过学生小组讨论,培养学生思考、团结合作的精神。
2、教学重难点
重点:利用二元一次方程组确定一次函数的表达式。
难点:应用二元一次方程组和函数的联系解决实际问题。
三、温故知新
1.确定正比例函数的表达式需要几个条件?
确定一次函数的表达式需要几个条件?
2.点A在正比例函数的图象上,这个正比例函数的表达式为_________。
3.已知一次函数经点和,求一次函数的解析式为__________。
四、学习过程
(一)探究活动
已知一次函数经过点和,求一次函数的解析式为_________。
解:设一次函数解析式为,
将 和分别代入得:,
解得:
所以一次函数的解析式为 。
总结:确定一次函数表达式的步骤是什么呢?
1.设:设一次函数表达式为 ;
2.代:将点的坐标代入中,列出关于k和b的方程或方程组;
3.解:解方程或方程组,求出k和b;
4.写:将所求得的k和b值代回表达式中,从而写出表达式。
这种求函数解析式的方法叫做待定系数法。
(二)例题解析
某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费y(元)是行李质量 x(kg)的一次函数.现知李明带了60 kg的行李,交了行李费5元;张华带了90 kg的行李,交了行李费10元。
(1)写出y与x之间的函数表达式;
(2)旅客最多可免费携带多少千克的行李?
解:(1)设一次函数解析式为 ,
由题意得:,解得:
所以y 与 x 之间的关系式为 。
(2)当y=0时,,解得:
答:旅客最多可免费携带30千克的行李。
(三)学以致用
在弹性限度内,弹簧的长度y(cm)是所挂物体质量 x(kg)的一次函数。当所挂物体的质量为1kg时,弹簧长15厘米;当所挂物体的质量为3 kg时,弹簧长16 cm。写出 y 与 x 之间的关系式,并求出所挂物体的质量为4 kg时弹簧的长度。
解:(1)设一次函数解析式为 ,
由题意得:,解得:
所以y 与 x 之间的关系式为 。
(2)当x=4时,y=0.5×4+14.5=16.5(cm)
答:所挂物体的质量为4 kg时弹簧的长度为16.5cm。
(四)拓展延伸
某市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若某户居民应交水费 y(元)与用水量x(吨)的函数关系如图所示。
(1)分别写出当0≤x≤15和x>15时,y与x的函数关系式;
(2)若某用户十月份用水量为10 吨,则应交水费多少元?若该用户十一月份交了51元的水费,则他该月用水多少吨?
解:(1)当0≤x≤15时,设y与x的函数关系式为y=k x,
则由题意得:27=15k,解得:k=1.8。所以y =1.8x。
当x>15时,设y与x的函数关系式为y=m x+n,则由题意得:,解得:
所以当x>15时,y=2.4x-9。
(2)当x=10时,y=1.8x=1.8×10=16(元),即应交水费为18元。
由于51>27,所以用水x>15。
所以当y=51时,51=2.4x-9,解得x=25。
若交51元的水费时,该月用水25吨。
(五)分组讨论
A,B两地相距100千米,甲、乙两人骑车同时分别从A,B两地相向而行.假设他们都保持匀速行驶,则他们各自到A地的距离S(千米)都是骑车时间t(时)的一次函数.1小时后乙距离A地80千米;2小时后甲距离A地30千米.问经过多长时间两人将相遇?
思考:1.根据以上所学内容,你能用几种方法解决以上问题?
2.图象法和代数法在解决问题时有什么不同?
五、课堂小结
1.函数与方程之间的关系;
2.掌握利用二元一次方程组求一次函数表达式的步骤:待定系数法
设 代 解 写
六.课后练习
1. 一次函数y=k x+b的图象与x轴、y轴的交点坐标分别是(2,0)和(0,-1),则这个函数的表达式子为 ( )
A. B.
C. D.
解:设,
将(2,0)和(0,-1)代入得:
解得:
所以函数的表达式为。
2. 已知函数y=2x+b的图象经过点(a,7)和(-2,a),则这个函数的表达式为 ( )
A. B.
C. D.
解:由于y=2x+b,
所以将(a,7)和(-2,a)分别代入得:
解得:。
所以y=2x+5。
3. 求出图中的两条直线 l1和l2的函数表达式。
解:设l1:y1=k1x+b1
把(0,1)和(1,3)分别代入得:
解得:.
所以l1:y1=2x+1.
设l1:y2=k2x+b2
把(4,0)和(0,4)分别代入得:
解得:
所以l2:y2=-x+4。
4.某饮料厂生产一种饮料,经测算,用一吨水生产的饮料利润(元)是一吨水的价格(元)的一次函数,根据下表提供的数据,求与的函数关系式;当水价为每吨10元时,一吨水生产出的饮料的利润是多少?
一吨水的价格/元 4 6
用一吨水生产的饮料所获利润/元 200 198
解:(1)设一次函数解析式为 ,
由题意得:
解得:。
所以y 与 x 之间的关系式为。
(2)当x=10时,y=-10+204=194(元)
所以一吨水生产出的饮料的利润是194元。
5.小明在暑期社会实践活动中,以每千克0.8元的价格从批发市场购进若干千克西瓜到市场上去销售,在销售了40千克西瓜之后,余下的以每千克降价0.4元全部售完。销售金额与售出西瓜的千克数之间的关系如图所示。
请你根据图象提供的信息完成以下问题:的函数关系如图所示。
(1)求降价前销售金额 y(元)与售出西瓜x(千克)之间的函数关系式;
(2)小明从批发市场共购进多少千克西瓜?
(3)小明这次卖瓜赚了多少钱?
解:(1)设函数关系式为,由题意得:,解得:。所以降价前销售金额 y(元)与售出西瓜x(千克)之间的函数关系式。
(2)(kg);(kg)。
所以小明从批发市场共购进70千克西瓜
(3)
所以小明这次卖瓜赚了20元。
七.教学反思
根据我对教材的理解,上课后的感受,进行教学反思。
1.在学习一次函数与一元一次方程、一元一次不等式之间的关系后进行一次函数与二元一次方程组关系的学习,学生对于解二元一次方程组比较有信心。
2.学生对函数与方程、不等式之间的关系有一定的认识,能通过函数图象理解它们之间的关系,但是课堂上利用函数图像理解一次函数与方程组之间的关系这一内容时间稍微少了一些。
3.班级学生喜欢解计算题,但是对应用题有一种惧怕心理,因此本节课重点是从简单的题出发,让学生了解什么是待定系数法,然后进一步层层递进,设置实际情境问题。
4.本节内容对学困生而言比较困难,这也是这节课的失败之处。此外,在教学的过程中,应对学困生进行及时的辅导。同时也需要注重学生的解题过程,引导学生发现解决问题的渠道。
1.设
4.写
3.解
2.代
设计意图:让学生分析题意,思考如何解决,通过简单的题目,让学生交流讨论总结如何确定一次函数的表达式。
设计意图:通过实际问题情境,注重引导学生分析问题,从实际情境中寻找确定函数表达式的条件,进一步加强函数与方程的联系,用待定系数法确定一次函数的表达式,突破本课重点,培养学生的逻辑思维能力。
设计意图:通过练习进行强化,目的在于加强学生“利用二元一次方程组确定一次函数解析式”。
x(吨)
y(元)
15
20
39
27
O
设计意图:让学生观察图象,从图象上获得信息,再用相关知识解决问题,培养学生的探究意识,在具体情境中利用图象提供的信息,承接上一章一次函数图像的应用,进一步强化学生数形结合的意识,学会从图形中获取有用的信息。
设计意图:通过实际问题情境,让学生在多种方法解决问题,思考和比较体会图象法和代数法各自的特点,理解知识之间的广泛联系。
设计意图:让学生归纳和总结本节所学的内容,进行总结和自我反思。
o
y
x
1
2
3
4
1
2
3
4
方法提示:求一次函数的表达式一般用待定系数法,这需要两个条件,如直线上的两个点的左边、两对函数值等,这就需要学生认真分析所给的条件,找出相应条件。让学生在学习中进一步体会二元一次方程组与一次函数之间的关系。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
