探索轴对称的性质

课件44张PPT。
探索轴对称的性质


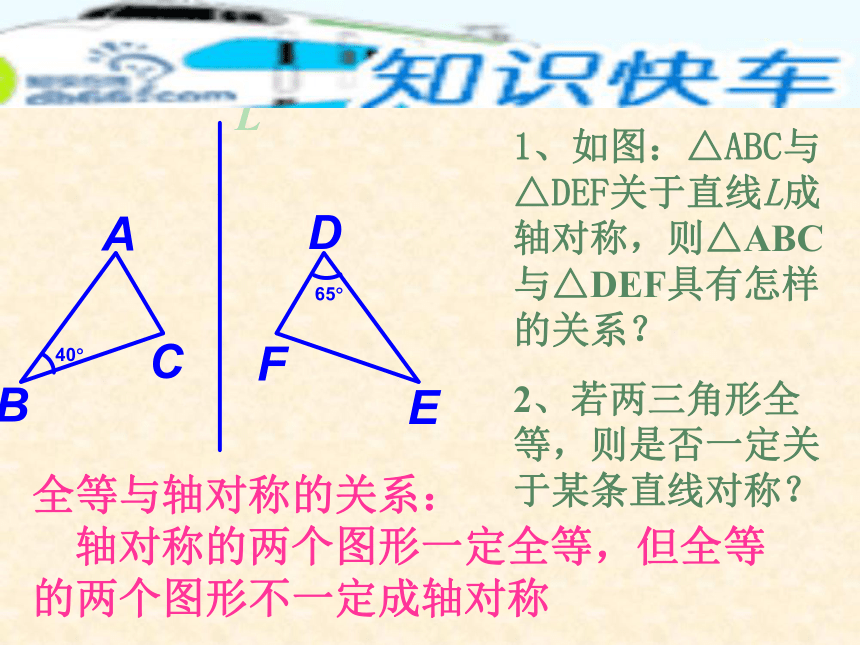
如果一个图形沿某条直线对折后，直线两旁的部分能够完全重合，那么这个图形叫做轴对称图形。轴对称图形：对于两个图形，把一个图形沿着某一条直线对折，如果它能够与另一个图形完全重合，那么就说这两个图形成轴对称。这条直线就是对称轴 轴对称：1、如图：△ABC与△DEF关于直线L成轴对称，则△ABC与△DEF具有怎样的关系？
2、若两三角形全等，则是否一定关于某条直线对称？L全等与轴对称的关系：
轴对称的两个图形一定全等，但全等的两个图形不一定成轴对称对应点：沿某条直线折叠后，能够重合的一对点叫对应点
对应边：沿某条直线折叠后，能够重合的一对边叫对应边
对应角：沿某条直线折叠后，能够重合的一对角叫对应角L“对称是一种思想，通过它，人们毕生追求，并创造次序、美丽和完善……”让我们走进轴对称的世界！去感受对称的奇妙和美丽吧！探索轴对称的性质车标设计交通标志实物图案练一练:1、在下列图形中，找出轴对称图形，并找出它的两组对应点。2.在下面的图形中找到轴对称图形,并找出它的两组对应线段.如图：将一张长方形形的纸对折，然后用笔尖扎出“14”这个数字，将纸打开后铺平：
打开
1、上图中，两个“14”有什么关系?
关于直线m成轴对称
m对应线段：相等 2、线段 AB与A′B′,CD与C′D′ 有什么关系？m打开 ∠1与∠2有什么关系？ ∠3与∠4呢？
对应角：相等打开m如果连接C、C′，F、F′那么所构造的线段与直线m有什么关系？对应点所连接的线段被对称轴垂直平分 打开m轴对称的性质1.对应点的连线被对称轴垂直平分2.对应线段相等，对应角相等 做一做：右图是一个轴对称图形：（1）你能找出它的对称轴吗?（2）连接点A与点A1的线段与对称轴有什么关系？连接点B与点B1的线段呢？对应点所连的线段被对称轴垂直平分。（3）线段AD与线段A1D1有什么关系？线段BC与B1C1呢？为什么？（4）∠1与∠2有什么关系? ∠ 3与∠4呢？说说你的理由？对应角相等。对应线段相等，后面还有智力测验，你想试一试吗？试一试：1、一次晚会上，主持人出了一道题目：“如何把 变成一个真正的等式"，很长时间没有人答出，小兰仅仅拿出了一面镜子，就很快解决了这道题目，你知道她是怎样做的吗？例：如图所示，AD为 △ABC 的高，∠B＝ 2∠C ，借助于轴对称的性质想一想：CD与AB＋BD相等吗？请说明你的理由。拓展练习答：相等，理由如下：
在DC上截取DE使DE＝DB，连接AE
∵AD⊥BE且DB＝DE ∴B、E关于AD对称
∴△ABD与△AED关于直线AD对称
∴ △ABD ≌ △AED ∴AB＝AE，∠AED＝ ∠B
又∵ ∠B＝2 ∠C ∴ ∠AED＝ 2 ∠C
而∠AED＝ ∠C ＋ ∠CAE ∴ ∠CAE ＝ ∠ C
∴AE＝CE ∴AB＝CE 故AB＋BD＝DE＋EC
即：AB＋BD＝CD课堂小结1、再次感受对称美
2、轴对称图形是一个图形关于某条直线对称
3、轴对称是两个图形关于某条直线对称
4、轴对称的性质：
⑴对应点的连线被对称轴垂直且平分
⑵对应边相等，对应角相等作业正式作业： 习题7.3 第2题课外作业: 轻巧夺冠
《探索轴对称图形的性质》A卷感谢语：谢谢各位老师的光临！感谢大家的支持！
您的鼓励是我前进的动力！
再见！