思维拓展 圆(试题)数学六年级上册人教版(含答案)
文档属性
| 名称 | 思维拓展 圆(试题)数学六年级上册人教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-15 10:53:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
思维拓展:圆(试题)数学六年级上册人教版
一、选择题
1.如图,圆从点A开始沿着直尺向右滚动一周到达点B,点B最接近数( )(π取3.14)。
A.10 B.11 C.12 D.13
2.计算一个半径是r的半圆周长,列式为( )。
A. B. C. D.
3.一个正常运行的时钟,时针长厘米.当这个时钟运行一天一夜后,钟面上时针的针尖走了( )。
A.厘米 B.厘米 C.厘米 D.厘米
4.如图,把一个圆尽量多的分成若干份,然后将其拼成一个近似的长方形,已知这个长方形的长约为56.52cm,则该长方形的宽约为( )cm。
A.6 B.9 C.18 D.36
5.有两个大小不同的圆,它们的直径都增加1cm,它们增加的周长相比,( )。
A.大圆增加得多 B.小圆增加得多 C.增加得一样多 D.无法判断
6.圆的直径由4cm增加到6cm,这个圆的面积增加了( )。
A.5π B.2π C.5 D.1
二、填空题
7.在一张长8cm,宽6cm的长方形纸上剪一个最大的圆,这个圆的面积是( )。
8.A圆的周长和B圆的周长之比为3∶5,AB圆半径之比为( ),面积之比为( )。
9.一个直径是10m的半圆形花坛的周长是( )m,面积是( )。
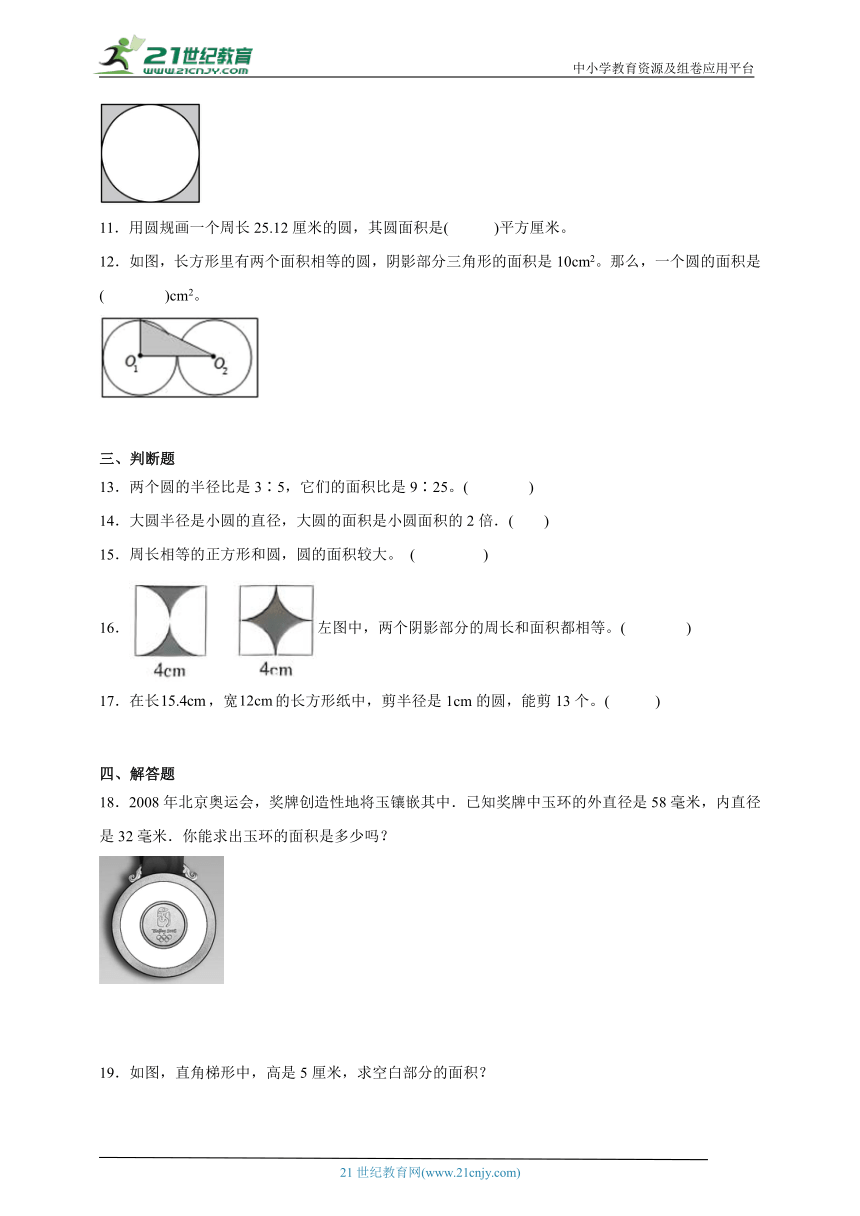
10.如图,在一张边长10cm的正方形纸上剪下一个最大的圆,这个圆的面积是( ),剩余部分的面积是( )。
11.用圆规画一个周长25.12厘米的圆,其圆面积是( )平方厘米。
12.如图,长方形里有两个面积相等的圆,阴影部分三角形的面积是10cm2。那么,一个圆的面积是( )cm2。
三、判断题
13.两个圆的半径比是3∶5,它们的面积比是9∶25。( )
14.大圆半径是小圆的直径,大圆的面积是小圆面积的2倍.( )
15.周长相等的正方形和圆,圆的面积较大。 ( )
16.左图中,两个阴影部分的周长和面积都相等。( )
17.在长,宽的长方形纸中,剪半径是1cm的圆,能剪13个。( )
四、解答题
18.2008年北京奥运会,奖牌创造性地将玉镶嵌其中.已知奖牌中玉环的外直径是58毫米,内直径是32毫米.你能求出玉环的面积是多少吗?
19.如图,直角梯形中,高是5厘米,求空白部分的面积?
20.有一个圆形的花坛,周长是37.68米,花坛外围有一条1米宽的观景小路。这条小路的面积是多少平方米?
21.一个圆形游乐场的周长是62.8米,扩建时,半径增加了1米,面积增加了多少平方米?
22.用三张同样大小的正方形白铁皮(边长是1.8米),分别按下面三种方式剪出不同规格的圆片。
(1)三种圆片中每个的周长分别是多少?
(2)剪完圆后,哪张白铁皮剩下的废料多?
(3)根据以上的计算,你发现了什么?
参考答案:
1.A
【分析】根据题意,圆从点A开始沿着直尺向右滚动一周到达点B,则点A到点B的距离等于圆的周长;圆的直径是(5-3)cm,根据圆的周长公式C=πd,求出A、B两点间的距离,再加上4,进而确定点B的位置。
【详解】圆的直径:5-3=2(cm)
圆的周长:3.14×2=6.28(cm)
4+6.28≈10(cm)
点B最接近数10。
故答案为:A
【点睛】本题考查圆的周长公式的运用,明确圆滚动一周走过的距离等于圆的周长。
2.D
【分析】如图:半圆的周长=圆的周长的一半+2r,圆的周长=,所以圆的周长的一半等于,据此解答。
【详解】根据分析得,半圆的周长==。
故答案为:D
【点睛】此题的解题关键是要分清求的是半圆的周长还是圆的周长的一半,灵活运用圆的周长公式求解。
3.B
【详解】略
4.C
【分析】根据圆面积公式的推导过程可知,把一个圆剪拼成一个近似长方形,这个长方形的长等于圆周长的一半,长方形的宽等于圆的半径,已知拼成的长方形的长是56.52cm,根据圆的周长公式:C=2πr,那么r=C÷π÷2,据此求出半径(也就是长方形的宽)。
【详解】56.52÷3.14=18(cm)
该长方形的宽是18cm。
故答案为:C
【点睛】此题考查的目的是理解掌握圆面积公式的推导过程及应用,圆的周长公式及应用。
5.C
【分析】假设小圆的直径为d,大圆的直径为D,它们的直径都增加1cm,小圆的直径变为(d+1)cm,大圆的直径变为(D+1)cm,再根据圆的周长公式:C=πd,分别求出这两个大小不同的圆增加的周长,再比较大小即可。
【详解】假设小圆的直径为d,大圆的直径为D,
小圆增加的周长为:
π×(d+1)-πd
=πd+π×1-πd
=π(cm)
大圆增加的周长为:
π×(D+1)-πD
=πD+π×1-πD
=π(cm)
可见两个大小不同的圆增加的周长都是πcm,增加的一样多。
故答案为:C
【点睛】此题的解题关键是灵活运用圆的周长公式解决实际的问题。
6.A
【分析】根据圆的面积公式:S=πr2,据此分别求出直径为4cm和6cm的圆的面积,再用变化后的面积减去变化前的面积即可。
【详解】(6÷2)2π-(4÷2)2π
=32π-22π
=9π-4π
=5π(cm2)
则这个圆的面积增加了5πcm2。
故答案为:A
【点睛】本题考查圆的面积,熟记公式是解题的关键。
7.28.26
【分析】以长方形的宽为直径的圆是长方形纸上最大的圆,利用“”求出这个圆的面积,据此解答。
【详解】3.14×(6÷2)2
=3.14×32
=3.14×9
=28.26()
所以,这个圆的面积是28.26。
【点睛】表示出圆的半径并掌握圆的面积计算公式是解答题目的关键。
8. 3∶5 9∶25
【分析】根据圆的周长公式C=2πr,求出AB两个圆的半径然后用A圆的半径比B的半径即可;根据圆的面积公式S=πr2,求出A圆的面积和B圆的面积,最后用A圆的面积比B圆的面积即可。
【详解】假设A圆的周长是3,B圆的周长是5,
A圆的半径:3÷π÷2=,B圆的半径:5÷π÷2=,
∶
=(×2π)∶(×2π)
=3∶5
A圆的面积:π×()2=,B圆的面积:π×()2=
∶
=(×4π)∶(×4π)
=9∶25
【点睛】本题考查圆的周长和面积,熟记公式是解题的关键。
9. 25.7 39.25
【分析】半圆的周长=圆周长的一半+一条直径的长度;半圆的面积=圆的面积÷2;据此解答。
【详解】周长:3.14×10÷2+10
=31.4÷2+10
=15.7+10
=25.7(米)
面积:3.14×(10÷2)2÷2
=3.14×25÷2
=78.5÷2
=39.25(平方米)
【点睛】半圆的周长与圆周长的一半不同,半圆的周长比圆周长的一半多一条直径的长度;半圆的面积等于圆的面积的一半。
10. 78.5 21.5
【分析】由题意可知:这个最大圆的直径应该等于正方形的边长,正方形的边长已知,于是利用圆的面积=πr2,即可求出圆的面积;再用正方形的面积减去圆的面积,即可求出剩余部分的面积。
【详解】3.14×(10÷2)2
=3.14×25
=78.5(平方厘米)
这个圆的面积是78.5平方厘米。
10×10-78.5
=100-78.5
=21.5(平方厘米)
余下部分的面积是21.5平方厘米。
【点睛】此题主要考查学生正方形与圆面积的计算能力,解答此题的关键是明白:正方形中最大圆的直径应该等于正方形的边长,即可求得圆面积和余下的面积。
11.50.24
【分析】圆的周长=,求出圆的半径,再根据圆的面积公式求出圆的面积即可。
【详解】25.12÷3.14÷2
=8÷2
=4(厘米)
3.14×4×4
=3.14×16
=50.24(平方厘米)
【点睛】本题考查圆的周长和面积,解答本题的关键是掌握圆的周长和面积计算公式。
12.31.4
【分析】图中直角三角形的两条直角边分别为圆半径和圆半径的2倍,根据已知的三角形面积,能求出圆半径的平方是多少,再根据圆面积公式“”即可求出圆面积。
【详解】解:设圆半径为rcm。
2r×r÷2=10
r2=10
3.14×10=31.4(cm2)
所以一个圆的面积是31.4cm2。
【点睛】解答此题的关键是看出阴影部分三角形的两条直角边分别为2r和r。
13.√
【分析】根据圆的面积公式:S=πr2,分别求出两个圆的面积,然后再求它们的比即可。
【详解】π×32∶π×52
=9π∶25π
=9∶25
所以它们的面积比是9∶25。原题干说法正确。
故答案为:√
【点睛】本题考查圆的面积,熟记公式是解题的关键。
14.×
【分析】由“圆的面积=πr2”可知,圆的面积比就等于半径平方的比,再据“大圆半径等于小圆直径”即可求得它们的面积倍数关系.
【详解】解:设小圆的半径为r,则大圆的半径2r;
则大圆面积是小圆面积的倍数:π(2r)2÷πr2=4倍;
答:大圆面积是小圆面积的4倍.
故答案为错误.
15.√
【分析】可设圆的周长为c,正方形的边长为x,圆的半径为r,因为圆的周长与正方形的周长相等,可根据圆的面积公式和正方形的面积公式进行计算后再比较大小即可得到答案。
【详解】设周长为c,正方形边长为x,圆半径为r
则c=4x=2πr
x=,r=,
正方形的面积为:x2=,
圆面积为:πr2=,
4π=4×3.14=12.56,
因为12.56<16,
所以圆的面积大于正方形的面积。
故答案为:√
16.×
【分析】第一个图形阴影部分的周长等于直径为4厘米的圆的周长加上两条正方形的边长,阴影部分的面积等于正方形的面积减去半径为(4÷2)厘米的圆的面积,利用正方形和圆的面积公式分别求出这两个图形的面积,再相减即可得解;
第二个图形阴影部分的周长等于直径为4厘米的圆的周长,阴影部分的面积等于正方形的面积减去半径为(4÷2)厘米的圆的面积,利用正方形和圆的面积公式分别求出这两个图形的面积,再相减即可得解。
【详解】第一个图形阴影部分的周长:
3.14×4+4×2
=12.56+8
=20.56(厘米)
第一个图形阴影部分的面积:
4×4-3.14×(4÷2)2
=16-3.14×22
=16-3.14×4
=16-12.56
=3.44(平方厘米)
第二个图形阴影部分的周长:
3.14×4=12.56(厘米)
第二个图形阴影部分的面积:
4×4-3.14×(4÷2)2
=16-3.14×22
=16-3.14×4
=16-12.56
=3.44(平方厘米)
所以两个阴影部分的周长不相等,面积相等。原题说法错误。
故答案为:×
【点睛】此题的解题关键是灵活运用圆的周长和面积公式求解。
17.×
【分析】圆的半径是1厘米,则直径是1×2=2(厘米)。沿长方形纸的长边来剪,可以剪15.4÷2≈7(个);沿宽边剪,可以剪12÷2=6(行)。每行剪7个,一共剪6行,则一共可以剪7×6=42(个)圆。
【详解】1×2=2(厘米)
15.4÷2≈7(个)
12÷2=6(行)
7×6=42(个)
这张长方形纸能剪42个圆。
故答案为:×
【点睛】求长方形能剪几个圆,要沿长和宽分别计算每行剪几个、能剪几行,再把每行的个数乘行数即可求出圆的总数。因为圆不能密铺,则不能用长方形的面积除以圆的面积求出圆的个数。
18.1836.9平方毫米
【详解】3.14×(58÷2)2-3.14×(32÷2)2
=3.14×585
=1836.9(平方毫米)
19.20.75平方厘米
【详解】试题分析:由题意可知:梯形的高就等于半圆的半径,梯形的高已知,也就等于知道了半圆的半径,进而可以求出半圆的直径,也就是梯形的上底,从而依据阴影部分的面积=梯形的面积﹣半圆的面积即可求解.
解:(5×2+14)×5÷2﹣3.14×52÷2,
=24×5÷2﹣78.5÷2,
=60﹣39.25,
=20.75(平方厘米);
答:空白部分的面积是20.75平方厘米.
点评:解答此题的关键是明白:梯形的高等于半圆的半径,梯形的上底等于半圆的直径.
20.40.82平方米
【分析】根据题意可知,求小路的面积就是求圆环的面积,先根据圆的周长C=2πr,用37.68÷3.14÷2求出圆形花坛的半径,即为小圆的半径,再用小圆的半径加1,求出花坛加上观景小路构成的大圆的半径,根据圆环面积S=π(R2-r2),把数据代入求解即可。
【详解】37.68÷3.14÷2
=12÷2
=6(米)
6+1=7(米)
3.14×(72-62)
=3.14×(49-36)
=3.14×13
=40.82(平方米)
答:这条小路的面积是40.82平方米。
【点睛】熟练掌握圆的周长和圆环的面积公式是解答本题的关键。
21.65.94平方米
【分析】根据题意可知,扩建时,半径增加了1米,求面积增加了多少平方米,也就是求这个环形的面积,已知内圆周长,首先求出内圆半径,根据环形面积=外圆面积-内圆面积,由此列式解答。
【详解】内圆半径:
62.8÷3.14÷2=10(米)
增加的面积:
3.14×[(10+1)2-102]
=3.14×[121-100]
=3.14×21
=65.94(平方米)
答:面积增加了65.94平方米。
【点睛】此题考查环形面积计算,根据环形面积公式:环形面积=外圆面积-内圆面积,或环形面积=3.14×(外圆半径的平方-内圆半径的平方)列式解答。
22.(1)5.652米;2.826米;1.884米
(2)同样多
(3)见详解
【分析】(1)第一种圆片的直径=正方形边长,第二种圆片的直径=正方形边长÷2,第三种圆片的直径=正方形边长÷3,根据圆的周长=πd,列式解答即可。
(2)剩下的废料面积=正方形面积-所有圆的面积,正方形面积=边长×边长,圆的面积=πr2,据此列式解答。
(3)根据剩下的废料的面积即可得出结论。
【详解】(1)1.8÷2=0.9(米)
1.8÷3=0.6(米)
第一种:3.14×1.8=5.652(米)
第二种:3.14×0.9=2.826(米)
第三种:3.14×0.6=1.884(米)
答:三种圆片中每个的周长分别是5.652米、2.826米、1.884米。
(2)1.8×1.8=3.24(平方米)
3.24-3.14×(1.8÷2)2
=3.24-3.14×0.92
=3.24-3.14×0.81
=3.24-2.5434
=0.6966(平方米)
3.24-3.14×(0.9÷2)2×4
=3.24-3.14×0.452×4
=3.24-3.14×0.2025×4
=3.24-2.5434
=0.6966(平方米)
3.24-3.14×(0.6÷2)2×9
=3.24-3.14×0.32×9
=3.24-3.14×0.09×9
=3.24-2.5434
=0.6966(平方米)
答:剪完圆后,三张白铁皮剩下的废料同样多。
(3)发现:按这三种方式剪完圆后,三张白铁皮剩下的废料同样多,这说明剪掉的圆的面积的和也是相等的。照此推测,按这样的方式剪圆片,无论怎样剪,剩下的废料总是不变的。
【点睛】关键是掌握并灵活运用圆的周长和面积公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
思维拓展:圆(试题)数学六年级上册人教版
一、选择题
1.如图,圆从点A开始沿着直尺向右滚动一周到达点B,点B最接近数( )(π取3.14)。
A.10 B.11 C.12 D.13
2.计算一个半径是r的半圆周长,列式为( )。
A. B. C. D.
3.一个正常运行的时钟,时针长厘米.当这个时钟运行一天一夜后,钟面上时针的针尖走了( )。
A.厘米 B.厘米 C.厘米 D.厘米
4.如图,把一个圆尽量多的分成若干份,然后将其拼成一个近似的长方形,已知这个长方形的长约为56.52cm,则该长方形的宽约为( )cm。
A.6 B.9 C.18 D.36
5.有两个大小不同的圆,它们的直径都增加1cm,它们增加的周长相比,( )。
A.大圆增加得多 B.小圆增加得多 C.增加得一样多 D.无法判断
6.圆的直径由4cm增加到6cm,这个圆的面积增加了( )。
A.5π B.2π C.5 D.1
二、填空题
7.在一张长8cm,宽6cm的长方形纸上剪一个最大的圆,这个圆的面积是( )。
8.A圆的周长和B圆的周长之比为3∶5,AB圆半径之比为( ),面积之比为( )。
9.一个直径是10m的半圆形花坛的周长是( )m,面积是( )。
10.如图,在一张边长10cm的正方形纸上剪下一个最大的圆,这个圆的面积是( ),剩余部分的面积是( )。
11.用圆规画一个周长25.12厘米的圆,其圆面积是( )平方厘米。
12.如图,长方形里有两个面积相等的圆,阴影部分三角形的面积是10cm2。那么,一个圆的面积是( )cm2。
三、判断题
13.两个圆的半径比是3∶5,它们的面积比是9∶25。( )
14.大圆半径是小圆的直径,大圆的面积是小圆面积的2倍.( )
15.周长相等的正方形和圆,圆的面积较大。 ( )
16.左图中,两个阴影部分的周长和面积都相等。( )
17.在长,宽的长方形纸中,剪半径是1cm的圆,能剪13个。( )
四、解答题
18.2008年北京奥运会,奖牌创造性地将玉镶嵌其中.已知奖牌中玉环的外直径是58毫米,内直径是32毫米.你能求出玉环的面积是多少吗?
19.如图,直角梯形中,高是5厘米,求空白部分的面积?
20.有一个圆形的花坛,周长是37.68米,花坛外围有一条1米宽的观景小路。这条小路的面积是多少平方米?
21.一个圆形游乐场的周长是62.8米,扩建时,半径增加了1米,面积增加了多少平方米?
22.用三张同样大小的正方形白铁皮(边长是1.8米),分别按下面三种方式剪出不同规格的圆片。
(1)三种圆片中每个的周长分别是多少?
(2)剪完圆后,哪张白铁皮剩下的废料多?
(3)根据以上的计算,你发现了什么?
参考答案:
1.A
【分析】根据题意,圆从点A开始沿着直尺向右滚动一周到达点B,则点A到点B的距离等于圆的周长;圆的直径是(5-3)cm,根据圆的周长公式C=πd,求出A、B两点间的距离,再加上4,进而确定点B的位置。
【详解】圆的直径:5-3=2(cm)
圆的周长:3.14×2=6.28(cm)
4+6.28≈10(cm)
点B最接近数10。
故答案为:A
【点睛】本题考查圆的周长公式的运用,明确圆滚动一周走过的距离等于圆的周长。
2.D
【分析】如图:半圆的周长=圆的周长的一半+2r,圆的周长=,所以圆的周长的一半等于,据此解答。
【详解】根据分析得,半圆的周长==。
故答案为:D
【点睛】此题的解题关键是要分清求的是半圆的周长还是圆的周长的一半,灵活运用圆的周长公式求解。
3.B
【详解】略
4.C
【分析】根据圆面积公式的推导过程可知,把一个圆剪拼成一个近似长方形,这个长方形的长等于圆周长的一半,长方形的宽等于圆的半径,已知拼成的长方形的长是56.52cm,根据圆的周长公式:C=2πr,那么r=C÷π÷2,据此求出半径(也就是长方形的宽)。
【详解】56.52÷3.14=18(cm)
该长方形的宽是18cm。
故答案为:C
【点睛】此题考查的目的是理解掌握圆面积公式的推导过程及应用,圆的周长公式及应用。
5.C
【分析】假设小圆的直径为d,大圆的直径为D,它们的直径都增加1cm,小圆的直径变为(d+1)cm,大圆的直径变为(D+1)cm,再根据圆的周长公式:C=πd,分别求出这两个大小不同的圆增加的周长,再比较大小即可。
【详解】假设小圆的直径为d,大圆的直径为D,
小圆增加的周长为:
π×(d+1)-πd
=πd+π×1-πd
=π(cm)
大圆增加的周长为:
π×(D+1)-πD
=πD+π×1-πD
=π(cm)
可见两个大小不同的圆增加的周长都是πcm,增加的一样多。
故答案为:C
【点睛】此题的解题关键是灵活运用圆的周长公式解决实际的问题。
6.A
【分析】根据圆的面积公式:S=πr2,据此分别求出直径为4cm和6cm的圆的面积,再用变化后的面积减去变化前的面积即可。
【详解】(6÷2)2π-(4÷2)2π
=32π-22π
=9π-4π
=5π(cm2)
则这个圆的面积增加了5πcm2。
故答案为:A
【点睛】本题考查圆的面积,熟记公式是解题的关键。
7.28.26
【分析】以长方形的宽为直径的圆是长方形纸上最大的圆,利用“”求出这个圆的面积,据此解答。
【详解】3.14×(6÷2)2
=3.14×32
=3.14×9
=28.26()
所以,这个圆的面积是28.26。
【点睛】表示出圆的半径并掌握圆的面积计算公式是解答题目的关键。
8. 3∶5 9∶25
【分析】根据圆的周长公式C=2πr,求出AB两个圆的半径然后用A圆的半径比B的半径即可;根据圆的面积公式S=πr2,求出A圆的面积和B圆的面积,最后用A圆的面积比B圆的面积即可。
【详解】假设A圆的周长是3,B圆的周长是5,
A圆的半径:3÷π÷2=,B圆的半径:5÷π÷2=,
∶
=(×2π)∶(×2π)
=3∶5
A圆的面积:π×()2=,B圆的面积:π×()2=
∶
=(×4π)∶(×4π)
=9∶25
【点睛】本题考查圆的周长和面积,熟记公式是解题的关键。
9. 25.7 39.25
【分析】半圆的周长=圆周长的一半+一条直径的长度;半圆的面积=圆的面积÷2;据此解答。
【详解】周长:3.14×10÷2+10
=31.4÷2+10
=15.7+10
=25.7(米)
面积:3.14×(10÷2)2÷2
=3.14×25÷2
=78.5÷2
=39.25(平方米)
【点睛】半圆的周长与圆周长的一半不同,半圆的周长比圆周长的一半多一条直径的长度;半圆的面积等于圆的面积的一半。
10. 78.5 21.5
【分析】由题意可知:这个最大圆的直径应该等于正方形的边长,正方形的边长已知,于是利用圆的面积=πr2,即可求出圆的面积;再用正方形的面积减去圆的面积,即可求出剩余部分的面积。
【详解】3.14×(10÷2)2
=3.14×25
=78.5(平方厘米)
这个圆的面积是78.5平方厘米。
10×10-78.5
=100-78.5
=21.5(平方厘米)
余下部分的面积是21.5平方厘米。
【点睛】此题主要考查学生正方形与圆面积的计算能力,解答此题的关键是明白:正方形中最大圆的直径应该等于正方形的边长,即可求得圆面积和余下的面积。
11.50.24
【分析】圆的周长=,求出圆的半径,再根据圆的面积公式求出圆的面积即可。
【详解】25.12÷3.14÷2
=8÷2
=4(厘米)
3.14×4×4
=3.14×16
=50.24(平方厘米)
【点睛】本题考查圆的周长和面积,解答本题的关键是掌握圆的周长和面积计算公式。
12.31.4
【分析】图中直角三角形的两条直角边分别为圆半径和圆半径的2倍,根据已知的三角形面积,能求出圆半径的平方是多少,再根据圆面积公式“”即可求出圆面积。
【详解】解:设圆半径为rcm。
2r×r÷2=10
r2=10
3.14×10=31.4(cm2)
所以一个圆的面积是31.4cm2。
【点睛】解答此题的关键是看出阴影部分三角形的两条直角边分别为2r和r。
13.√
【分析】根据圆的面积公式:S=πr2,分别求出两个圆的面积,然后再求它们的比即可。
【详解】π×32∶π×52
=9π∶25π
=9∶25
所以它们的面积比是9∶25。原题干说法正确。
故答案为:√
【点睛】本题考查圆的面积,熟记公式是解题的关键。
14.×
【分析】由“圆的面积=πr2”可知,圆的面积比就等于半径平方的比,再据“大圆半径等于小圆直径”即可求得它们的面积倍数关系.
【详解】解:设小圆的半径为r,则大圆的半径2r;
则大圆面积是小圆面积的倍数:π(2r)2÷πr2=4倍;
答:大圆面积是小圆面积的4倍.
故答案为错误.
15.√
【分析】可设圆的周长为c,正方形的边长为x,圆的半径为r,因为圆的周长与正方形的周长相等,可根据圆的面积公式和正方形的面积公式进行计算后再比较大小即可得到答案。
【详解】设周长为c,正方形边长为x,圆半径为r
则c=4x=2πr
x=,r=,
正方形的面积为:x2=,
圆面积为:πr2=,
4π=4×3.14=12.56,
因为12.56<16,
所以圆的面积大于正方形的面积。
故答案为:√
16.×
【分析】第一个图形阴影部分的周长等于直径为4厘米的圆的周长加上两条正方形的边长,阴影部分的面积等于正方形的面积减去半径为(4÷2)厘米的圆的面积,利用正方形和圆的面积公式分别求出这两个图形的面积,再相减即可得解;
第二个图形阴影部分的周长等于直径为4厘米的圆的周长,阴影部分的面积等于正方形的面积减去半径为(4÷2)厘米的圆的面积,利用正方形和圆的面积公式分别求出这两个图形的面积,再相减即可得解。
【详解】第一个图形阴影部分的周长:
3.14×4+4×2
=12.56+8
=20.56(厘米)
第一个图形阴影部分的面积:
4×4-3.14×(4÷2)2
=16-3.14×22
=16-3.14×4
=16-12.56
=3.44(平方厘米)
第二个图形阴影部分的周长:
3.14×4=12.56(厘米)
第二个图形阴影部分的面积:
4×4-3.14×(4÷2)2
=16-3.14×22
=16-3.14×4
=16-12.56
=3.44(平方厘米)
所以两个阴影部分的周长不相等,面积相等。原题说法错误。
故答案为:×
【点睛】此题的解题关键是灵活运用圆的周长和面积公式求解。
17.×
【分析】圆的半径是1厘米,则直径是1×2=2(厘米)。沿长方形纸的长边来剪,可以剪15.4÷2≈7(个);沿宽边剪,可以剪12÷2=6(行)。每行剪7个,一共剪6行,则一共可以剪7×6=42(个)圆。
【详解】1×2=2(厘米)
15.4÷2≈7(个)
12÷2=6(行)
7×6=42(个)
这张长方形纸能剪42个圆。
故答案为:×
【点睛】求长方形能剪几个圆,要沿长和宽分别计算每行剪几个、能剪几行,再把每行的个数乘行数即可求出圆的总数。因为圆不能密铺,则不能用长方形的面积除以圆的面积求出圆的个数。
18.1836.9平方毫米
【详解】3.14×(58÷2)2-3.14×(32÷2)2
=3.14×585
=1836.9(平方毫米)
19.20.75平方厘米
【详解】试题分析:由题意可知:梯形的高就等于半圆的半径,梯形的高已知,也就等于知道了半圆的半径,进而可以求出半圆的直径,也就是梯形的上底,从而依据阴影部分的面积=梯形的面积﹣半圆的面积即可求解.
解:(5×2+14)×5÷2﹣3.14×52÷2,
=24×5÷2﹣78.5÷2,
=60﹣39.25,
=20.75(平方厘米);
答:空白部分的面积是20.75平方厘米.
点评:解答此题的关键是明白:梯形的高等于半圆的半径,梯形的上底等于半圆的直径.
20.40.82平方米
【分析】根据题意可知,求小路的面积就是求圆环的面积,先根据圆的周长C=2πr,用37.68÷3.14÷2求出圆形花坛的半径,即为小圆的半径,再用小圆的半径加1,求出花坛加上观景小路构成的大圆的半径,根据圆环面积S=π(R2-r2),把数据代入求解即可。
【详解】37.68÷3.14÷2
=12÷2
=6(米)
6+1=7(米)
3.14×(72-62)
=3.14×(49-36)
=3.14×13
=40.82(平方米)
答:这条小路的面积是40.82平方米。
【点睛】熟练掌握圆的周长和圆环的面积公式是解答本题的关键。
21.65.94平方米
【分析】根据题意可知,扩建时,半径增加了1米,求面积增加了多少平方米,也就是求这个环形的面积,已知内圆周长,首先求出内圆半径,根据环形面积=外圆面积-内圆面积,由此列式解答。
【详解】内圆半径:
62.8÷3.14÷2=10(米)
增加的面积:
3.14×[(10+1)2-102]
=3.14×[121-100]
=3.14×21
=65.94(平方米)
答:面积增加了65.94平方米。
【点睛】此题考查环形面积计算,根据环形面积公式:环形面积=外圆面积-内圆面积,或环形面积=3.14×(外圆半径的平方-内圆半径的平方)列式解答。
22.(1)5.652米;2.826米;1.884米
(2)同样多
(3)见详解
【分析】(1)第一种圆片的直径=正方形边长,第二种圆片的直径=正方形边长÷2,第三种圆片的直径=正方形边长÷3,根据圆的周长=πd,列式解答即可。
(2)剩下的废料面积=正方形面积-所有圆的面积,正方形面积=边长×边长,圆的面积=πr2,据此列式解答。
(3)根据剩下的废料的面积即可得出结论。
【详解】(1)1.8÷2=0.9(米)
1.8÷3=0.6(米)
第一种:3.14×1.8=5.652(米)
第二种:3.14×0.9=2.826(米)
第三种:3.14×0.6=1.884(米)
答:三种圆片中每个的周长分别是5.652米、2.826米、1.884米。
(2)1.8×1.8=3.24(平方米)
3.24-3.14×(1.8÷2)2
=3.24-3.14×0.92
=3.24-3.14×0.81
=3.24-2.5434
=0.6966(平方米)
3.24-3.14×(0.9÷2)2×4
=3.24-3.14×0.452×4
=3.24-3.14×0.2025×4
=3.24-2.5434
=0.6966(平方米)
3.24-3.14×(0.6÷2)2×9
=3.24-3.14×0.32×9
=3.24-3.14×0.09×9
=3.24-2.5434
=0.6966(平方米)
答:剪完圆后,三张白铁皮剩下的废料同样多。
(3)发现:按这三种方式剪完圆后,三张白铁皮剩下的废料同样多,这说明剪掉的圆的面积的和也是相等的。照此推测,按这样的方式剪圆片,无论怎样剪,剩下的废料总是不变的。
【点睛】关键是掌握并灵活运用圆的周长和面积公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
