思维拓展 数与形(试题)数学六年级上册人教版(含答案)
文档属性
| 名称 | 思维拓展 数与形(试题)数学六年级上册人教版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-15 11:34:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
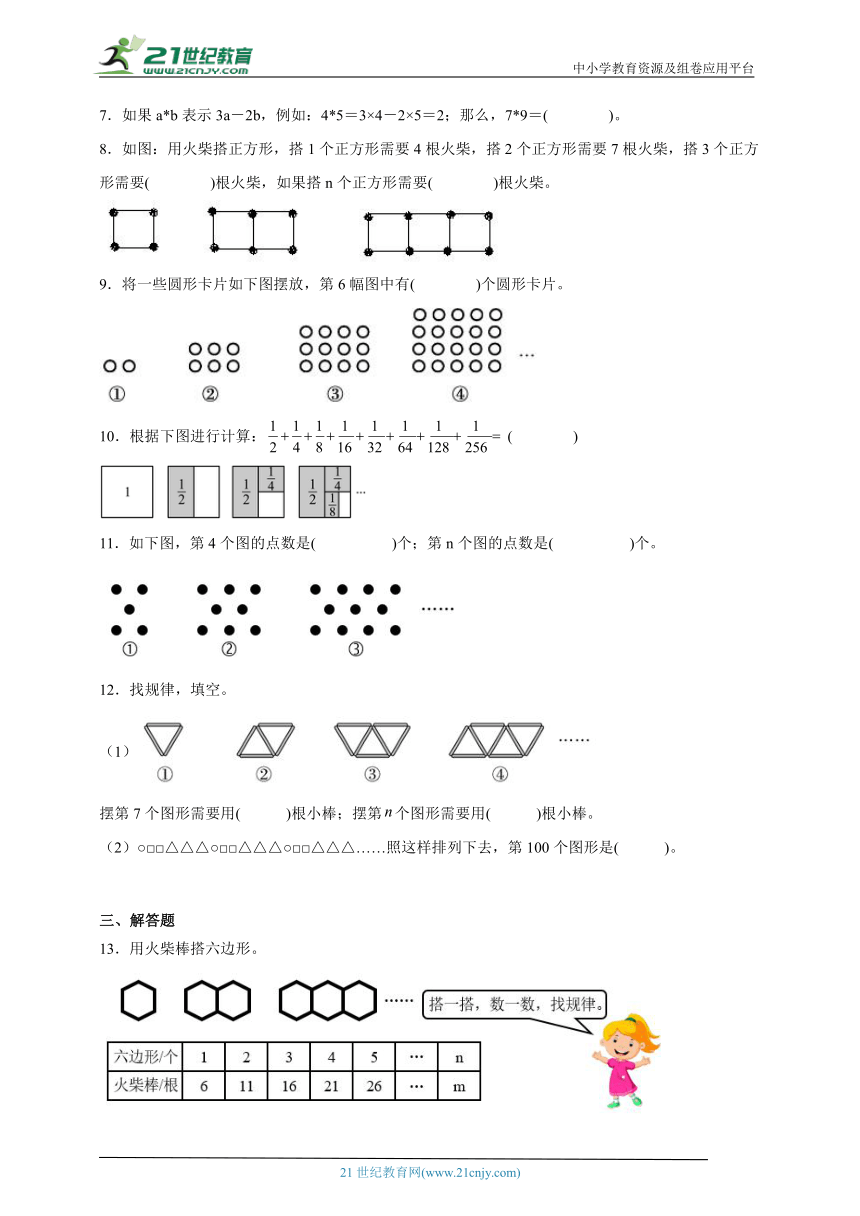
思维拓展:数与形(试题)数学六年级上册人教版
一、选择题
1.在学校最近进行的乒乓球比赛中,每两个同学之间都要进行一场比赛,共进行了66场比赛,那么这次比赛一共有( )个同学参加。
A.10 B.11 C.12
2.用小棒按照如下方式摆图形,摆n个八边形需要( )根小棒。
A.8n B.8n-1 C.7n+1 D.8(n-1)
3.用木杆搭建围栏。按照下面的规律搭下去,第⑦幅图用( )根木杆。
……
A.26 B.28 C.30
4.观察下面点阵图的规律,第6幅点阵图中有( )个点。
……
A.18 B.21 C.24 D.27
5.用小木棒按下图方式摆放图形,第⑧个图形需要( )根小木棒。
A.33 B.30 C.36 D.27
6.如下图,第5个图形是由( )个小正方形拼成的。
A.16 B.20 C.25 D.36
二、填空题
7.如果a*b表示3a-2b,例如:4*5=3×4-2×5=2;那么,7*9=( )。
8.如图:用火柴搭正方形,搭1个正方形需要4根火柴,搭2个正方形需要7根火柴,搭3个正方形需要( )根火柴,如果搭n个正方形需要( )根火柴。
9.将一些圆形卡片如下图摆放,第6幅图中有( )个圆形卡片。
10.根据下图进行计算:( )
11.如下图,第4个图的点数是( )个;第n个图的点数是( )个。
12.找规律,填空。
(1)
摆第7个图形需要用( )根小棒;摆第个图形需要用( )根小棒。
(2)○□□△△△○□□△△△○□□△△△……照这样排列下去,第100个图形是( )。
三、解答题
13.用火柴棒搭六边形。
(1)m=__________。
(2)用2016根火柴棒能搭成多少个六边形?
14.搭建如图(1)的单顶帐篷需要17根钢管,若这样的帐篷按图(2)、图(3)的方式串起来搭建,则可节省结合处的钢管,那么串搭20顶这样的帐篷需要多少根钢管?
15.拼成一个等腰三角形要用5根火柴棒,每条腰用两根,底用一根火柴棒。拼成2个这样的等腰三角形要用8根火柴棒(两个三角形拼在一起),拼成3个这样的等腰三角形要用11根火柴棒,那么拼成n个这样的等腰三角形至少要多少根火柴棒。
16.观察算式的规律:,,,,……。用含字母的式子表示规律:( )。
用规律计算:( )。
17.某机器有依次排列的5盏灯,每盏灯可发出红色的光(用■表示),不同位置上的灯光表示一个具体的数,下面是四种情况所表示的数。
■□□□□→1;□■□□□→2;■■■□□→7=1+2+4;■□■□■→21=1+4+16
(1)通过观察比较发现:5盏灯中最中间的一盏灯为红色时表示的数是( )。
(2)根据上面的规律,算出下面两种情况所表示的数。(直接填结果)
□□■■■→( )■■□■□→( )
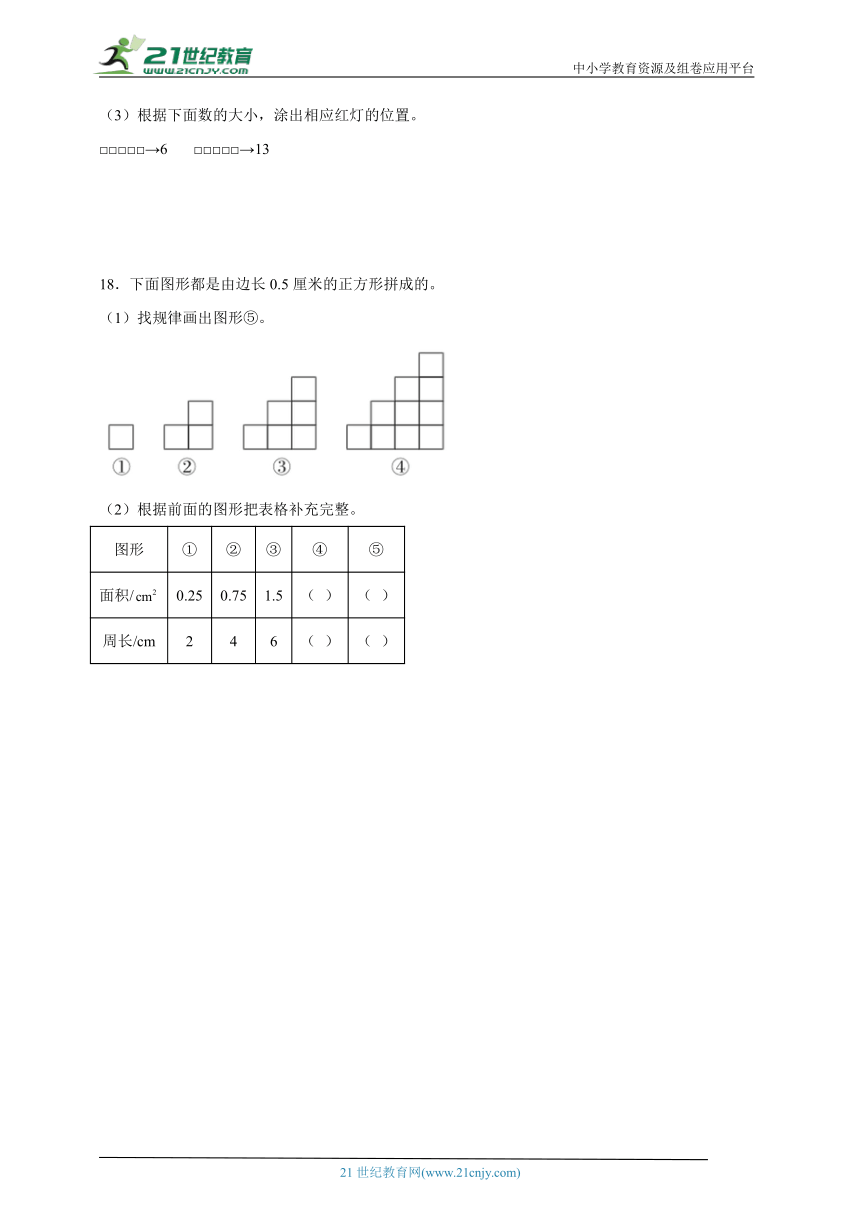
(3)根据下面数的大小,涂出相应红灯的位置。
□□□□□→6 □□□□□→13
18.下面图形都是由边长0.5厘米的正方形拼成的。
(1)找规律画出图形⑤。
(2)根据前面的图形把表格补充完整。
图形 ① ② ③ ④ ⑤
面积/ 0.25 0.75 1.5 ( ) ( )
周长/cm 2 4 6 ( ) ( )
参考答案:
1.C
【分析】本题属于握手问题,其公式为人数×(人数-1)÷2=比赛次数。设人数为x,则x(x-1)÷2=66,据此求出人数即可。
【详解】x(x-1)÷2=66
则:x(x-1)=132;
A.当x=10时,10×(10-1)=90,不符合;
B.当x=11时,11×(11-1)=110,不符合;
C.当x=12时,12×(12-1)=132,符合;
那么这次比赛一共有(12)个同学参加。
故答案为:C
【点睛】熟练掌握握手问题的公式是解答本题的关键。
2.C
【分析】根据图示发现:摆1个八边形需要小棒:8根;摆2个八边形需要小棒(8+7)根;摆3个八边形需要小棒(8+7+7)根;……摆n个八边形需要小棒的根数是8+7(n-1)。据此解答。
【详解】8+7(n-1)
=8+7n-7
=(7n+1)根
摆n个八边形需要(7n+1)根小棒。
故答案为:C
【点睛】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题。
3.C
【分析】看图,每幅图都是在上一幅图的基础上增加4根木杆。第①幅图用2+4×1=6(根)木杆,第②幅图用2+4×2=10(根)木杆,第③幅图用2+4×3=14(根)木杆。据此类推,那么第⑦幅图需要用(2+4×7)根木杆。
【详解】2+4×7
=2+28
=30(根)
所以,第⑦幅图用30根木杆。
故答案为:C
【点睛】本题考查了数与形,有一定观察总结能力是解题的关键。
4.B
【分析】通过观察,第1幅点阵图中有(3+3)个点,第2幅点阵图中有(3+3+3)个点;第3幅点阵图中有(3+3+3+3)个点……以此类推,可得出第n幅点阵图中有(3+3n)个点,据此解答。
【详解】据分析可知,第n幅点阵图中有(3+3n)个点;
第6幅点阵图中有
3+3×6
=3+18
=21(个)
第6幅点阵图中有21个点。
故答案为:B
【点睛】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题。
5.D
【分析】第1个图形需要6根小木棒,第2个图形需要(6+3)根小木棒,第3个图形需要(6+3×2)根小木棒……每增加一个正方形增加3根小木棒,第n个图形需要[6+3×(n-1)]根小木棒,最后求出n=8时式子的值,据此解答。
【详解】第n个图形需要小木棒的数量:6+3×(n-1)
=6+3n-3×1
=6+3n-3
=3n+6-3
=(3n+3)根
当n=8时。
3n+3
=3×8+3
=24+3
=27(根)
所以,第⑧个图形需要27根小木棒。
故答案为:D
【点睛】本题主要考查数形结合思想的应用,找出小木棒数量的变化规律是解答题目的关键。
6.C
【分析】观察图形,第1个图形是由1×1=1=12个小正方形拼成的,第2个图形是由2×2=4=22个小正方形拼成的,第3个图形是由3×3=9=32个小正方形拼成的,依次类推,可以看出第5个图形是由52个小正方形拼成的。据此解答。
【详解】52=5×5=25(个)
即第5个图形是由25个小正方形拼成的。
故答案为:C
【点睛】此题的解题关键是利用数与形的结合,通过观察图形,把图形中变化的规律转化成数字,多多练习,培养数感。
7.3
【分析】根据所给的运算方法,将7*9写成a*b=3a-2b的形式,进行解答即可。
【详解】由a*b=3a-2b可得:
7*9
=3×7-2×9
=21-18
=3
【点睛】解答此题的关键是,根据题意找出运算方法,再根据运算方法,列式解答即可。
8. 10 3n+1
【分析】由图可知,搭1个正方形需要4根火柴,搭2个正方形需要(4+3)根火柴,搭3个正方形需要(4+3×2)根火柴……每增加一个正方形需要增加3根火柴,那么搭n个正方形需要[4+(n-1)×3]根火柴,最后求出n=3时含有字母式子的值,据此解答。
【详解】搭n个正方形需要火柴的数量:4+(n-1)×3
=4+3n-3
=3n+(4-3)
=(3n+1)根
当n=3时。
3n+1
=3×3+1
=9+1
=10(根)
所以,搭3个正方形需要10根火柴,如果搭n个正方形需要(3n+1)根火柴。
【点睛】根据图形找出正方形个数和火柴根数的变化规律是解答题目的关键。
9.42
【分析】从第一个图形开始分析小圆圈的个数:第一个图形中有1×2=2(个)圆形卡片,第二个图形中有2×3=6(个)圆形卡片,第三个图形中有3×4=12(个)圆形卡片,第四个图形中有4×5=20(个)圆形卡片,…第n个图形有n(n+1)个圆形卡片,利用规律解决问题。
【详解】观察图形可知:
第一个图形中有1×2=2(个)
第二个图形中有2×3=6(个)
第三个图形中有3×4=12(个)
第四个图形中有4×5=20(个)
…
所以第六幅图形有6×7=42(个)
【点睛】此题主要考查了图形的规律,通过归纳与总结结合图形得出图形个数之间的规律是解决问题的关键。
10.
【分析】由图可知, ; ,据此解答。
【详解】1- =
【点睛】此题考查了数与形,根据图形找出算式的规律是解题关键。
11. 14 3n+2/2+3n
【分析】观察可知,点数的个数=第几个图形就用几×3+2,据此分析。
【详解】4×3+2
=12+2
=14(个)
n×3+2=3n+2
第4个图的点数是14个;第n个图的点数是(3n+2)个。
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
12. 15 △
【分析】(1)观察图形可知:1个三角形所需火柴棍的根数=3,
2个三角形所需火柴棍的根数=3+2,
3个三角形所需火柴棍的根数=3+2×2,
…
n个三角形所需火柴棍的根数=3+2×(n-1)=2n+1。
当n=7时,2n+1=2×7+1=15(根)。
(2)根据题干可得,图形的排列是按照1个○,2个□,3个△,6个图形为一个周期;第100个图形是100÷6=16……4,即第17周期的第四个图形,与第一周期的第四个图形相同。
【详解】(1)2×7+1=15(根)
n个三角形所需火柴棍的根数=3+2×(n-1)=2n+1。
(2)100÷6=16(周期)……4(个)
第100个图形是△。
【点睛】(1)此题考查图形的变换规律;得到每个图形中火柴的根数与图形的个数的关系是解决本题的关键。
(2)此题根据题干得出图形的排列周期,然后利用这个周期特点进行推理计算。
13.(1)(5n+1)根;(2)403个
【分析】(1)观察图形,第一个六边形需要6根火柴棒,第二个六边形需要(6+5)根火柴棒,第三个六边形需要(6+5×2)根火柴棒,第四个六边形需要(6+5×3)根火柴棒,依次类推,第个六边形需要根火柴棒。据此表示出m的值。
(2)把火柴棒的根数2016根代入到上述公式中,利用等式的性质,解方程,即可求出能搭成多少个六边形。
【详解】(1)
=
=
=(5n+1)根
所以m=(5n+1)根
(2)5n+1=2016
解:5n=2016-1
5n=2015
n=2015÷5
n=403
答:用2016根火柴棒能搭成403个六边形。
【点睛】此题的解题关键是利用数与形的结合,通过观察图形,把图形中变化的规律转化成数字,多多练习,培养数感。
14.226根
【分析】通过观察发现:帐篷的左侧面需要6根钢管。图(1)需要6+11=17(根)钢管;图(2)需要6+11×2=28(根)钢管;图(3)需要6+11×3=39(根)钢管;……由此发现规律:图(n)需要(6+11n)根钢管。据此求串搭20顶这样的帐篷需要多少根钢管列式为6+11×20。
【详解】6+11×20
=6+220
=226(根)
答:串搭20顶这样的帐篷需要226根钢管。
【点睛】在运用数形结合的方法探究数学规律时,一定要把图形和数一一对应。
15.(3n+2)根
【分析】由题意可知,第一个等腰三角形用了5=2×2+1根火柴棒,第二个等腰三角形用了8=2×3+2根火柴棒,第三个等腰三角形用了11=2×4+3根火柴棒,…,由此得出第n个等腰三角形用了2×(n+1)+n根火柴棒,据此解答
【详解】第一个等腰三角形用了5=2×2+1根火柴棒,
第二个等腰三角形用了8=2×3+2根火柴棒,
第三个等腰三角形用了11=2×4+3根火柴棒,…
所以,第n个等腰三角形用了2×(n+1)+n=3n+2根火柴棒;
答:拼成n个这样的等腰三角形至少要(3n+2)根火柴棒。
【点睛】此题主要考查了图形的变化规律,注意结合图形发现蕴含的运算规律,找出解决问题的途径。
16. n2 (n 1)2=n+n+1 210
【分析】观察题目给出的算式,发现前一个数都比后一个数大1,而且前一个数的平方减去后一个数的平方最终等于前数加后数,由此可得到规律。
【详解】(1)n2 (n 1)2=n+n+1
(2)
=20+19+18+17+……+2+1
=20×10+10
=200+10
=210
【点睛】本题考查学生的观察能力,找到规律然后利用规律是解题的关键。
17.(1)4;(2)28;11;(3)见详解
【分析】(1)由已知的四种情况可知有以下规律:左起第一盏发出红光表示1,后面每一盏灯发出红光时表示的数是前一盏灯的2倍,当几盏灯同时发出红光时表示的数是这几盏灯分别表示的数的和;
(2)根据第(1)题的规律,第1个涂色表示1,第2个涂色表示2,第3个涂色表示4,第4个涂色表示8,第5个涂色表示16,根据此规律按题目要求把已经涂色的红灯表示的数相加即可得解;
(3)根据6=2+4,把第2个和第3个涂色,根据13=1+4+8,把第1个、第3个和第4个方框涂色,据此解答即可。
【详解】(1)1×2=2
2×2=4
4×2=8
8×2=16
所以5盏灯中最中间的一盏灯为红色时表示的数是4。
(2)4+8+16=28
1+2+8=11
所以□□■■■→28,■■□■□→11。
(3)6=2+4
13=1+4+8
所以发红光的灯的位置如下:
□■■□□→6
■□■■□→13
【点睛】解答此题的关键在于通过已知的例子找出每盏灯发红光时表示的数,再根据规律解答。
18.(1)见详解
(2)面积:2.5、3.75。
周长:8、10。
【分析】(1)观察图形可知,第一个图形有1列有1个正方形,第二个图形有2列,第2列有2个正方形,第三个图形有3列,第3列有3个正方形 所以第五个图形有5列,第5列有5个正方形;
(2)一个正方形的边长是0.5厘米,一个正方形的面积是0.5×0.5=0.25平方厘米,然后用一个正方形的面积乘正方形的个数即可;通过平移可知求图形4和图形5的周长即求边长是0.5×4=2厘米和0.5×5=2.5厘米正方形的周长。
【详解】(1)图形⑤如图所示:
(2)第④图形的面积为:0.5×0.5×10=2.5(平方厘米)
周长是:0.5×4×4=8(厘米)
第⑤图形的面积为:
0.5×0.5×15
=0.25×15
=3.75(平方厘米)
0.5×5×4
=2.5×4
=10(厘米)
【点睛】本题考查图形的周长和面积,明确面积和周长的定义是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
思维拓展:数与形(试题)数学六年级上册人教版
一、选择题
1.在学校最近进行的乒乓球比赛中,每两个同学之间都要进行一场比赛,共进行了66场比赛,那么这次比赛一共有( )个同学参加。
A.10 B.11 C.12
2.用小棒按照如下方式摆图形,摆n个八边形需要( )根小棒。
A.8n B.8n-1 C.7n+1 D.8(n-1)
3.用木杆搭建围栏。按照下面的规律搭下去,第⑦幅图用( )根木杆。
……
A.26 B.28 C.30
4.观察下面点阵图的规律,第6幅点阵图中有( )个点。
……
A.18 B.21 C.24 D.27
5.用小木棒按下图方式摆放图形,第⑧个图形需要( )根小木棒。
A.33 B.30 C.36 D.27
6.如下图,第5个图形是由( )个小正方形拼成的。
A.16 B.20 C.25 D.36
二、填空题
7.如果a*b表示3a-2b,例如:4*5=3×4-2×5=2;那么,7*9=( )。
8.如图:用火柴搭正方形,搭1个正方形需要4根火柴,搭2个正方形需要7根火柴,搭3个正方形需要( )根火柴,如果搭n个正方形需要( )根火柴。
9.将一些圆形卡片如下图摆放,第6幅图中有( )个圆形卡片。
10.根据下图进行计算:( )
11.如下图,第4个图的点数是( )个;第n个图的点数是( )个。
12.找规律,填空。
(1)
摆第7个图形需要用( )根小棒;摆第个图形需要用( )根小棒。
(2)○□□△△△○□□△△△○□□△△△……照这样排列下去,第100个图形是( )。
三、解答题
13.用火柴棒搭六边形。
(1)m=__________。
(2)用2016根火柴棒能搭成多少个六边形?
14.搭建如图(1)的单顶帐篷需要17根钢管,若这样的帐篷按图(2)、图(3)的方式串起来搭建,则可节省结合处的钢管,那么串搭20顶这样的帐篷需要多少根钢管?
15.拼成一个等腰三角形要用5根火柴棒,每条腰用两根,底用一根火柴棒。拼成2个这样的等腰三角形要用8根火柴棒(两个三角形拼在一起),拼成3个这样的等腰三角形要用11根火柴棒,那么拼成n个这样的等腰三角形至少要多少根火柴棒。
16.观察算式的规律:,,,,……。用含字母的式子表示规律:( )。
用规律计算:( )。
17.某机器有依次排列的5盏灯,每盏灯可发出红色的光(用■表示),不同位置上的灯光表示一个具体的数,下面是四种情况所表示的数。
■□□□□→1;□■□□□→2;■■■□□→7=1+2+4;■□■□■→21=1+4+16
(1)通过观察比较发现:5盏灯中最中间的一盏灯为红色时表示的数是( )。
(2)根据上面的规律,算出下面两种情况所表示的数。(直接填结果)
□□■■■→( )■■□■□→( )
(3)根据下面数的大小,涂出相应红灯的位置。
□□□□□→6 □□□□□→13
18.下面图形都是由边长0.5厘米的正方形拼成的。
(1)找规律画出图形⑤。
(2)根据前面的图形把表格补充完整。
图形 ① ② ③ ④ ⑤
面积/ 0.25 0.75 1.5 ( ) ( )
周长/cm 2 4 6 ( ) ( )
参考答案:
1.C
【分析】本题属于握手问题,其公式为人数×(人数-1)÷2=比赛次数。设人数为x,则x(x-1)÷2=66,据此求出人数即可。
【详解】x(x-1)÷2=66
则:x(x-1)=132;
A.当x=10时,10×(10-1)=90,不符合;
B.当x=11时,11×(11-1)=110,不符合;
C.当x=12时,12×(12-1)=132,符合;
那么这次比赛一共有(12)个同学参加。
故答案为:C
【点睛】熟练掌握握手问题的公式是解答本题的关键。
2.C
【分析】根据图示发现:摆1个八边形需要小棒:8根;摆2个八边形需要小棒(8+7)根;摆3个八边形需要小棒(8+7+7)根;……摆n个八边形需要小棒的根数是8+7(n-1)。据此解答。
【详解】8+7(n-1)
=8+7n-7
=(7n+1)根
摆n个八边形需要(7n+1)根小棒。
故答案为:C
【点睛】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题。
3.C
【分析】看图,每幅图都是在上一幅图的基础上增加4根木杆。第①幅图用2+4×1=6(根)木杆,第②幅图用2+4×2=10(根)木杆,第③幅图用2+4×3=14(根)木杆。据此类推,那么第⑦幅图需要用(2+4×7)根木杆。
【详解】2+4×7
=2+28
=30(根)
所以,第⑦幅图用30根木杆。
故答案为:C
【点睛】本题考查了数与形,有一定观察总结能力是解题的关键。
4.B
【分析】通过观察,第1幅点阵图中有(3+3)个点,第2幅点阵图中有(3+3+3)个点;第3幅点阵图中有(3+3+3+3)个点……以此类推,可得出第n幅点阵图中有(3+3n)个点,据此解答。
【详解】据分析可知,第n幅点阵图中有(3+3n)个点;
第6幅点阵图中有
3+3×6
=3+18
=21(个)
第6幅点阵图中有21个点。
故答案为:B
【点睛】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题。
5.D
【分析】第1个图形需要6根小木棒,第2个图形需要(6+3)根小木棒,第3个图形需要(6+3×2)根小木棒……每增加一个正方形增加3根小木棒,第n个图形需要[6+3×(n-1)]根小木棒,最后求出n=8时式子的值,据此解答。
【详解】第n个图形需要小木棒的数量:6+3×(n-1)
=6+3n-3×1
=6+3n-3
=3n+6-3
=(3n+3)根
当n=8时。
3n+3
=3×8+3
=24+3
=27(根)
所以,第⑧个图形需要27根小木棒。
故答案为:D
【点睛】本题主要考查数形结合思想的应用,找出小木棒数量的变化规律是解答题目的关键。
6.C
【分析】观察图形,第1个图形是由1×1=1=12个小正方形拼成的,第2个图形是由2×2=4=22个小正方形拼成的,第3个图形是由3×3=9=32个小正方形拼成的,依次类推,可以看出第5个图形是由52个小正方形拼成的。据此解答。
【详解】52=5×5=25(个)
即第5个图形是由25个小正方形拼成的。
故答案为:C
【点睛】此题的解题关键是利用数与形的结合,通过观察图形,把图形中变化的规律转化成数字,多多练习,培养数感。
7.3
【分析】根据所给的运算方法,将7*9写成a*b=3a-2b的形式,进行解答即可。
【详解】由a*b=3a-2b可得:
7*9
=3×7-2×9
=21-18
=3
【点睛】解答此题的关键是,根据题意找出运算方法,再根据运算方法,列式解答即可。
8. 10 3n+1
【分析】由图可知,搭1个正方形需要4根火柴,搭2个正方形需要(4+3)根火柴,搭3个正方形需要(4+3×2)根火柴……每增加一个正方形需要增加3根火柴,那么搭n个正方形需要[4+(n-1)×3]根火柴,最后求出n=3时含有字母式子的值,据此解答。
【详解】搭n个正方形需要火柴的数量:4+(n-1)×3
=4+3n-3
=3n+(4-3)
=(3n+1)根
当n=3时。
3n+1
=3×3+1
=9+1
=10(根)
所以,搭3个正方形需要10根火柴,如果搭n个正方形需要(3n+1)根火柴。
【点睛】根据图形找出正方形个数和火柴根数的变化规律是解答题目的关键。
9.42
【分析】从第一个图形开始分析小圆圈的个数:第一个图形中有1×2=2(个)圆形卡片,第二个图形中有2×3=6(个)圆形卡片,第三个图形中有3×4=12(个)圆形卡片,第四个图形中有4×5=20(个)圆形卡片,…第n个图形有n(n+1)个圆形卡片,利用规律解决问题。
【详解】观察图形可知:
第一个图形中有1×2=2(个)
第二个图形中有2×3=6(个)
第三个图形中有3×4=12(个)
第四个图形中有4×5=20(个)
…
所以第六幅图形有6×7=42(个)
【点睛】此题主要考查了图形的规律,通过归纳与总结结合图形得出图形个数之间的规律是解决问题的关键。
10.
【分析】由图可知, ; ,据此解答。
【详解】1- =
【点睛】此题考查了数与形,根据图形找出算式的规律是解题关键。
11. 14 3n+2/2+3n
【分析】观察可知,点数的个数=第几个图形就用几×3+2,据此分析。
【详解】4×3+2
=12+2
=14(个)
n×3+2=3n+2
第4个图的点数是14个;第n个图的点数是(3n+2)个。
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
12. 15 △
【分析】(1)观察图形可知:1个三角形所需火柴棍的根数=3,
2个三角形所需火柴棍的根数=3+2,
3个三角形所需火柴棍的根数=3+2×2,
…
n个三角形所需火柴棍的根数=3+2×(n-1)=2n+1。
当n=7时,2n+1=2×7+1=15(根)。
(2)根据题干可得,图形的排列是按照1个○,2个□,3个△,6个图形为一个周期;第100个图形是100÷6=16……4,即第17周期的第四个图形,与第一周期的第四个图形相同。
【详解】(1)2×7+1=15(根)
n个三角形所需火柴棍的根数=3+2×(n-1)=2n+1。
(2)100÷6=16(周期)……4(个)
第100个图形是△。
【点睛】(1)此题考查图形的变换规律;得到每个图形中火柴的根数与图形的个数的关系是解决本题的关键。
(2)此题根据题干得出图形的排列周期,然后利用这个周期特点进行推理计算。
13.(1)(5n+1)根;(2)403个
【分析】(1)观察图形,第一个六边形需要6根火柴棒,第二个六边形需要(6+5)根火柴棒,第三个六边形需要(6+5×2)根火柴棒,第四个六边形需要(6+5×3)根火柴棒,依次类推,第个六边形需要根火柴棒。据此表示出m的值。
(2)把火柴棒的根数2016根代入到上述公式中,利用等式的性质,解方程,即可求出能搭成多少个六边形。
【详解】(1)
=
=
=(5n+1)根
所以m=(5n+1)根
(2)5n+1=2016
解:5n=2016-1
5n=2015
n=2015÷5
n=403
答:用2016根火柴棒能搭成403个六边形。
【点睛】此题的解题关键是利用数与形的结合,通过观察图形,把图形中变化的规律转化成数字,多多练习,培养数感。
14.226根
【分析】通过观察发现:帐篷的左侧面需要6根钢管。图(1)需要6+11=17(根)钢管;图(2)需要6+11×2=28(根)钢管;图(3)需要6+11×3=39(根)钢管;……由此发现规律:图(n)需要(6+11n)根钢管。据此求串搭20顶这样的帐篷需要多少根钢管列式为6+11×20。
【详解】6+11×20
=6+220
=226(根)
答:串搭20顶这样的帐篷需要226根钢管。
【点睛】在运用数形结合的方法探究数学规律时,一定要把图形和数一一对应。
15.(3n+2)根
【分析】由题意可知,第一个等腰三角形用了5=2×2+1根火柴棒,第二个等腰三角形用了8=2×3+2根火柴棒,第三个等腰三角形用了11=2×4+3根火柴棒,…,由此得出第n个等腰三角形用了2×(n+1)+n根火柴棒,据此解答
【详解】第一个等腰三角形用了5=2×2+1根火柴棒,
第二个等腰三角形用了8=2×3+2根火柴棒,
第三个等腰三角形用了11=2×4+3根火柴棒,…
所以,第n个等腰三角形用了2×(n+1)+n=3n+2根火柴棒;
答:拼成n个这样的等腰三角形至少要(3n+2)根火柴棒。
【点睛】此题主要考查了图形的变化规律,注意结合图形发现蕴含的运算规律,找出解决问题的途径。
16. n2 (n 1)2=n+n+1 210
【分析】观察题目给出的算式,发现前一个数都比后一个数大1,而且前一个数的平方减去后一个数的平方最终等于前数加后数,由此可得到规律。
【详解】(1)n2 (n 1)2=n+n+1
(2)
=20+19+18+17+……+2+1
=20×10+10
=200+10
=210
【点睛】本题考查学生的观察能力,找到规律然后利用规律是解题的关键。
17.(1)4;(2)28;11;(3)见详解
【分析】(1)由已知的四种情况可知有以下规律:左起第一盏发出红光表示1,后面每一盏灯发出红光时表示的数是前一盏灯的2倍,当几盏灯同时发出红光时表示的数是这几盏灯分别表示的数的和;
(2)根据第(1)题的规律,第1个涂色表示1,第2个涂色表示2,第3个涂色表示4,第4个涂色表示8,第5个涂色表示16,根据此规律按题目要求把已经涂色的红灯表示的数相加即可得解;
(3)根据6=2+4,把第2个和第3个涂色,根据13=1+4+8,把第1个、第3个和第4个方框涂色,据此解答即可。
【详解】(1)1×2=2
2×2=4
4×2=8
8×2=16
所以5盏灯中最中间的一盏灯为红色时表示的数是4。
(2)4+8+16=28
1+2+8=11
所以□□■■■→28,■■□■□→11。
(3)6=2+4
13=1+4+8
所以发红光的灯的位置如下:
□■■□□→6
■□■■□→13
【点睛】解答此题的关键在于通过已知的例子找出每盏灯发红光时表示的数,再根据规律解答。
18.(1)见详解
(2)面积:2.5、3.75。
周长:8、10。
【分析】(1)观察图形可知,第一个图形有1列有1个正方形,第二个图形有2列,第2列有2个正方形,第三个图形有3列,第3列有3个正方形 所以第五个图形有5列,第5列有5个正方形;
(2)一个正方形的边长是0.5厘米,一个正方形的面积是0.5×0.5=0.25平方厘米,然后用一个正方形的面积乘正方形的个数即可;通过平移可知求图形4和图形5的周长即求边长是0.5×4=2厘米和0.5×5=2.5厘米正方形的周长。
【详解】(1)图形⑤如图所示:
(2)第④图形的面积为:0.5×0.5×10=2.5(平方厘米)
周长是:0.5×4×4=8(厘米)
第⑤图形的面积为:
0.5×0.5×15
=0.25×15
=3.75(平方厘米)
0.5×5×4
=2.5×4
=10(厘米)
【点睛】本题考查图形的周长和面积,明确面积和周长的定义是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
