思维拓展 用字母表示数(试题)数学五年级上册苏教版(含答案)
文档属性
| 名称 | 思维拓展 用字母表示数(试题)数学五年级上册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-15 14:10:10 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
思维拓展:用字母表示数(试题)数学五年级上册苏教版
一、选择题
1.小明的爸爸今年a岁,小明今年(a-27)岁,再过3年,他们相差( )岁。
A.3 B.24 C.27 D.30
2.数a、b在直线上的位置如下图所示。下列式子中,得数最接近2的是( )。
A.a+b B.b-a C.a×b D.b÷a
3.把5(X+8)错写成了5X+8,结果比原来( )。
A.多8 B.少8 C.少32 D.多32
4.古希腊著名的毕达哥拉斯学派把1、3、6、10、15、21…这样的数称为“三角形数”,而把1、4、9、16、25、36…这样的数称为“正方形数”。从下图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻的“三角形数”之和。下列等式中,不符合这一规律的是( )。
A.25=9+16 B.36=15+21 C.49=21+28 D.64=28+36
5.用同样长的小棒摆正方形(每条边用一根小棒),照这样摆,摆n个正方形需要( )根小棒。
A.4n B.3n C.4n+2 D.3n+1
6.当三角形的三边存在下列关系:两边的平方和等于第三边的平方,我们把满足这样条件的三角形叫直角三角形。如:若32+42=52,则3、4、5可以组成一个直角三角形。下列三角形的三边能组成直角三角形的是( )。
A.2、3、4 B.6、8、9 C.5、6、7 D.5、12、13
二、填空题
7.师徒两人共同加工一批零件,徒弟每小时加工35个,师傅每小时加工a个。a-35表示( ),4小时两人共加工( )个。
8.ab都是非零自然数,且a÷b=5,则a和b的最大公因数是( ),最小公倍数是( )。
9.苗族千人长桌宴是苗族宴席的最高形式与隆重礼仪,已有几千年的历史。通常用于接亲嫁女、满月酒以及村寨联谊宴饮活动。在设定座位时如下图设计,认真观察,完成后面的问题。
(1)按照上图所示规律,安排5张桌子最多可以坐( )人。
(2)如果安排n张桌子,那么可坐人数可以用式子( )表示。
10.有8个竹筐,每个竹筐装a只小兔,一共可装( )只小兔。
11.研究人员发现,蟋蟀每分钟叫的次数与当地气温之间有如下关系:t=h÷3(t表示当地气温,h表示蟋蟀每分钟叫的次数)。如果测得蟋蟀每分钟大约叫105次,那么当地气温是( )℃;如果测得当地气温是21℃,那么此时蟋蟀每分钟大约( )次。
12.这里有一系列由小正方体搭成的塔。
下面是每个塔的平面示意图,图中的数字表示在垂直方向上有几个小正方体。
搭成“塔6”需要( )个小正方体。
三、判断题
13.等腰三角形的顶角是a°,则一个底角是180°-a°。( )
14.当时,。( )
15.9与x的8倍的和列式为(9+x)×8。( )
16.五(1)班有女生x人,男生人数是女生人数的0.4倍,五(1)班共有学生0.4x人。( )
17.方程6x+5=41与方程7.5x-27=18的解相同。( )
四、解答题
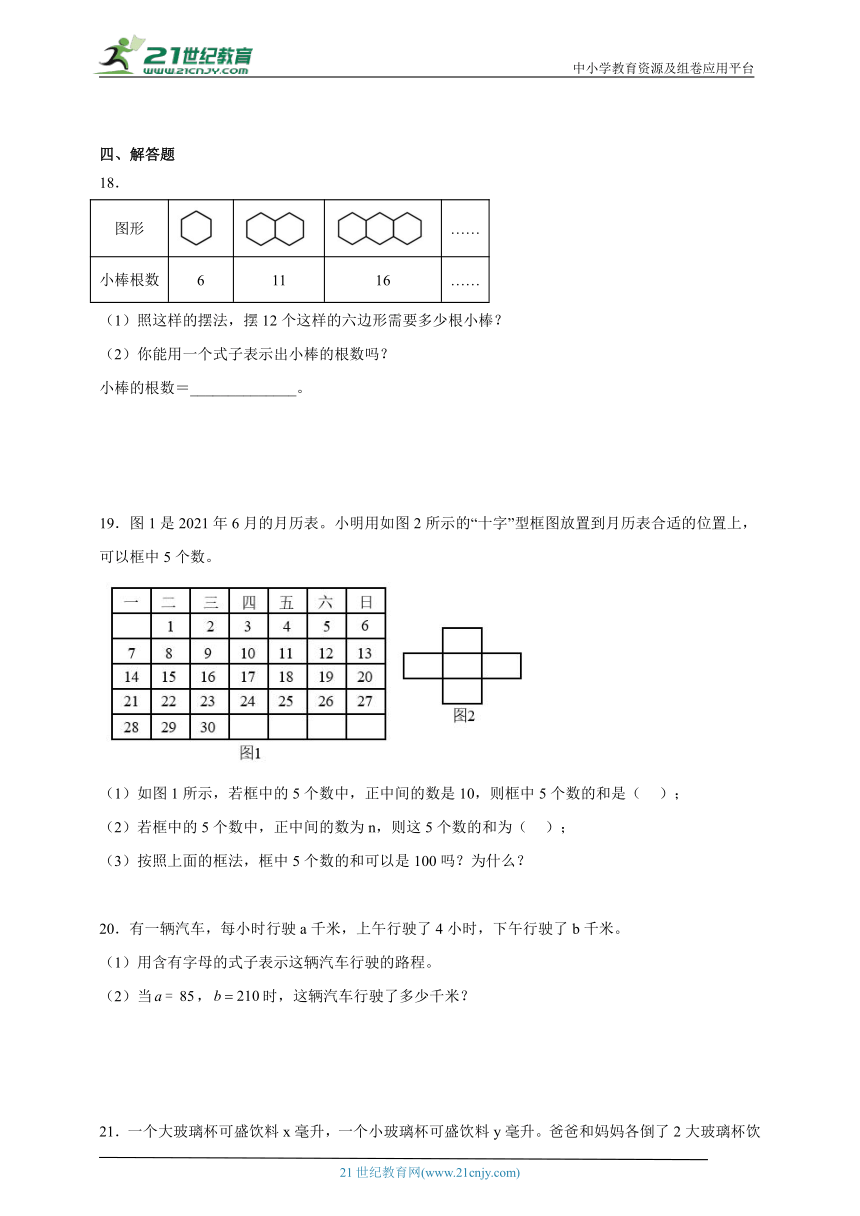
18.
图形 ……
小棒根数 6 11 16 ……
(1)照这样的摆法,摆12个这样的六边形需要多少根小棒?
(2)你能用一个式子表示出小棒的根数吗?
小棒的根数=______________。
19.图1是2021年6月的月历表。小明用如图2所示的“十字”型框图放置到月历表合适的位置上,可以框中5个数。
(1)如图1所示,若框中的5个数中,正中间的数是10,则框中5个数的和是( );
(2)若框中的5个数中,正中间的数为n,则这5个数的和为( );
(3)按照上面的框法,框中5个数的和可以是100吗?为什么?
20.有一辆汽车,每小时行驶a千米,上午行驶了4小时,下午行驶了b千米。
(1)用含有字母的式子表示这辆汽车行驶的路程。
(2)当,时,这辆汽车行驶了多少千米?
21.一个大玻璃杯可盛饮料x毫升,一个小玻璃杯可盛饮料y毫升。爸爸和妈妈各倒了2大玻璃杯饮料,东东倒了3小玻璃杯饮料。
(1)用含有字母的式子表示爸爸、妈妈和东东一共倒了多少毫升饮料。
(2)当x=150,y=100时,他们一共倒了多少毫升饮料?
22.甲车的速度是x千米/小时,乙车的速度是y千米/小时。两车同时从A地出发前往B地,5小时后甲车到达B地。
(1)用含x和y的式子表示此时甲、乙两车之间的距离。
(2)当x=80,y=65时,求两车之间的距离。
参考答案:
1.C
【分析】根据年龄差不会随时间的变化而改变,所以他们今年的年龄差就是3年后他们的年龄差。
【详解】a-(a-27)
=a-a+27
=27(岁)
小明的爸爸今年a岁,小明今年(a-27)岁,再过3年,他们相差27岁。
故答案为:C
【点睛】理解年龄差不随时间的变化而改变是解答此题的关键。
2.D
【分析】根据数a、b在数轴上的位置可知,0<a<b<1,且a接近0,b接近1;由此设a=0.4,b=0.7代入四个选项的式子中,计算出结果,再比较大小即可。
【详解】根据0<a<b<1,设a=0.4,b=0.7;
A.a+b;0.4+0.7=1.1;
B.b-a;0.7-0.4=0.3
C.a×b;0.4×0.7=0.28
D.b÷a;0.7÷0.4=1.75
1.75最接近2。
数a、b在直线上的位置如下图所示。下列式子中,得数最接近2的是b÷a。
故答案为:D
【点睛】根据a、b在数轴上的位置,用赋值法更直观地得出结论。
3.C
【分析】先运用乘法分配律把5(X+8)改写成5X+5×8;5×8-8=32,5X+8的结果比原来少32,即可解答。
【详解】5(X+8)-(5X+8)
=5X+5×8-5X-8
=40-8
=32
把5(X+8)错写成了5X+8,结果比原来少32。
故答案为:C
【点睛】本题考查含义字母的式子的化简,根据乘法分配律把5(X+8)进行改写是解题的关键。
4.A
【分析】根据“三角形数”的规律是:1,3,6,10,15,21,28,36,45…,而“正方形数”是两个相邻“三角形数”之和,据此逐项判断即可。
【详解】A.25=9+16;25=52,是正方形数,9和16不是三角形数,不符合规律,符合题意;
B.36=15+21;36=62,是正方形数,15和21是相邻的三角形数,符合规律,不符合题意;
C.49=21+28;49=72,是正方形数,21和28是相邻的三角形数,符合规律,不符合题意;
D.64=28+36;64=82,是正方形数,28和36是相邻的三角形数,符合规律,不符合题意。
故答案为:A
【点睛】解答本题的关键是找清楚“三角形数”和“正方形数”的关系,从而进行求解。
5.D
【分析】根据图,摆1个正方形需要4根小棒,摆2个正方形需要(4+3)根小棒,摆3个正方形需要(4+3+3)根小棒,由此可得摆n个正方形需要小棒数量为:4+(n-1)×3,根据答题。
【详解】由分析可得:
摆1个正方形需要:4根小棒;
摆2个正方形需要:4+3=7(根)
摆2个正方形需要:4+3+3=10(根)
……
摆n个正方形需要:
4+(n-1)×3
=4+3n-3
=(3n+1)根
故答案为:D
【点睛】解决本题的关键通过观察给出的图片,找出图片之间的数量关系,得出规律,再根据规律去解决问题。
6.D
【分析】根据题意可知,在直角三角形内,两条直角边的平方和等于斜边的平方,据此计算每个选项是否符合即可。
【详解】A.22+32
=4+9
=13
42=16
13≠16
2、3、4不能组成直角三角形;
B.62+82
=36+64
=100
92=81
100≠81
6、8、9不能组成直角三角形;
C.52+62
=25+36
=61
72=49
61≠49
5、6、7不能组成直角三角形;
D.52+122
=25+144
=169
132=169
169≠169
5、12、13能组成直角三角形。
故答案为:D
【点睛】本题主要考查了直角三角形的认识以及三边关系的应用。
7. 师傅比徒弟每小时多加工多少个 4a+140
【分析】由题意得a-35表示师傅比徒弟每小时多加工多少个;两人1小时共加工(a+35)个,乘4就是4小时共加工的个数。
【详解】a-35表示师傅比徒弟每小时多加工多少个,4小时两人共加工:(4a+140)个。
【点睛】此题考查了用字母表示数的方法,关键是弄清题中字母所表示的意义,再进一步解答。
8. b a
【详解】略
【分析】明确a是b的倍数,b是a的因数。则a,b两数的最大公因数是b,最小公倍数是a。
9.(1)22
(2)4n+2
【分析】(1)观察图形可知,安排1张桌子,可坐6人;安排2张桌子,可坐10人;安排3张桌子,可坐14人……发现:每增加一张桌子,可坐的人数增加4人,据此得出安排5张桌子最多可以坐的人数。
(2)由上一题,可得出:6=4×1+2,10=4×2+2,14=4×3+2……,据此找到规律,并按规律解答。
【详解】(1)安排1张桌子,可坐6人;
安排2张桌子,可坐6+4=10(人);
安排3张桌子,可坐10+4=14(人);
安排4张桌子,可坐14+4=18(人);
安排5张桌子,可坐18+4=22(人);
按照上图所示规律,安排5张桌子最多可以坐22人。
(2)安排1张桌子,可坐6人,6=4×1+2;
安排2张桌子,可坐10人,10=4×2+2;
安排3张桌子,可坐14人,14=4×3+2;
……
如果安排n张桌子,那么可坐人数可以用式子(4n+2)表示。
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
10.8a
【解析】略
11. 35 63
【分析】由题意得,蟋蟀每分钟大约叫105次,即h=105,求t的值;如果测得当地气温是21℃,即t=21,求h的值。
【详解】当h=105时,
t=105÷3
=35(℃);
当t=21时,
h=21×3
=63(次)
研究人员发现,蟋蟀每分钟叫的次数与当地气温之间有如下关系:t=h÷3(t表示当地气温,h表示蟋蟀每分钟叫的次数)。如果测得蟋蟀每分钟大约叫105次,那么当地气温是35℃;如果测得当地气温是21℃,那么此时蟋蟀每分钟大约63次。
【点睛】掌握用字母表示数的意义是解题关键。
12.56
【分析】第一个塔有1个小正方体,第二个塔有(2+1×2)个小正方体,第三个塔有(3+2×2+1×3)个小正方体,第四个塔有(4+3×2+2×3+1×4)个小正方体,则第五个塔有(5+4×2+3×3+2×4+1×5)个小正方体,第六个塔有(6+5×2+4×3+3×4+2×5+1×6)个小正方体。
【详解】6+5×2+4×3+3×4+2×5+1×6
=6+10+12+12+10+6
=16+12+12+10+6
=28+12+10+16
=40+10+6
=50+6
=56(个)
搭成“塔6”需要(56)个小正方体。
【点睛】本题主要考查数与形结合的规律,关键是根据所给图示,找出规律,并根据规律解题。
13.×
【分析】三角形内角和是180°,等腰三角形的有2个相等的底角和1个顶角,据此可知:等腰三角形的一个底角=(180°-顶角)÷2,据此解答。
【详解】(180°-a°)÷2
等腰三角形的顶角是a°,则一个底角是(180°-a°)÷2。
原题干说法错误。
故答案为:×
【点睛】掌握三角形内角和、等腰三角形的特征以及字母表示数的方法是解答本题的关键。
14.×
【分析】把代入计算,观察结果是否等于47即可。
【详解】把代入中,
=
=
=
当时,。原题干说法错误。
故答案为:×
【点睛】本题主要考查了含未知数式子的求值,把x的值代入式子计算即可。
15.×
【分析】先用x乘8,求出x的8倍,然后再加上9,然后与原题中的式子作比较即可判断。
【详解】9与x的8倍的和列式为:
9+x×8=9+8x
(9+x)×8=9×8+8x=72+8x
72+8x=9+8x
所以题干说法错误。
故答案为:×
【点睛】本题考查了字母表示数,要分清楚数量之间的关系,先求什么再求什么,找清列式的顺序,列出算式或方程计算。
16.×
【分析】根据题意,先求出五(1)班的男生人数,也就是求女生x人的0.4倍是多少,进而再加上女生人数,就是五(1)班全班人数。
【详解】x+x×0.4
=x+0.4x
=1.4x(人)
即五(1)班共有学生 1.4x人,所以原题答案错误。
故答案为:×
【点睛】此题考查用字母表示数,关键是用含字母的式子表示出男生人数,再加上女生人数得解。
17.√
【分析】利用等式的性质求出两个方程的解,看两个解是否相同即可。
【详解】6x+5=41
解:6x+5-5=41-5
6x÷6=36÷6
x=6
7.5x-27=18
解:7.5x-27+27=18+27
7.5x÷7.5=45÷7.5
x=6
方程6x+5=41与方程7.5x-27=18的解相同。
原题说法正确。
故答案为:√
【点睛】本题考查了方程的解法,解题过程要利用等式的性质。
18.(1)50根;(2)2+4n(n表示第n个图形)
【分析】观察图形以及其小棒根数可知:
摆第1个图形需要(2+4×1)根小棒;
摆第2个图形需要(2+4×2)根小棒;
摆第3个图形需要(2+4×3)根小棒;
以此类推
……
摆第12个图形需要(2+4×12)根小棒;
……
摆第n个图形需要(2+4n)根小棒。
【详解】(1)2+4×12
=2+48
=50(根)
答:需要50根小棒。
(2)小棒的根数=2+4n(n表示第n个图形)(答案不唯一)
用式子表示为小棒的根数=2+4n(n表示第n个图形)。
【点睛】本题的关键是要找到图形的小棒根数变化部分的共同点,以此推断出其规律。
19.(1)50;
(2)5n;
(3)不可以;理由见详解
【分析】(1)当正中间的数为10时,框中的5个数分别为3、10、17、9、11,用加法求出这个5个数的和;
(2)当正中间的数为n时,n上面的数为(n-7),n下面的数为(n+7),n左面的数为(n-1),n右面的数为(n+1),用含有n的式子表示出这5个数的和;
(3)正中间的数为框中这5个数的平均数,根据这5个数的和为100求出正中间的数,根据正中间的数确定其它4个数是否存在,据此解答。
【详解】(1)
3+9+10+11+17
=12+10+11+17
=22+11+17
=33+17
=50
所以,框中5个数的和是50。
(2)n-7+n+7+n-1+n+1+n
=n+n+n+n+n-7+7-1+1
=(n+n+n+n+n)-(7-7+1-1)
=5n
所以,这5个数的和为5n。
(3)100÷5=20
由上可知,框中5个数的和不可以是100,因为框中5个数的和为100时,正中间的数为20,但月历表中20的右面没有数字。
【点睛】月历表中上下相邻两个数的差是7,左右相邻两个数的差是1,根据框中的数与数之间的关系,用正中间的数表示出其它4个数是解答题目的关键。
20.(1)()千米
(2)550千米
【分析】(1)根据路程=速度×时间;用a×4,求出上午行驶的路程,再加上下午行驶的路程,即可求出这辆汽车行驶的路程;
(2)当a=85,b=210时,代入(1),求出结果即可。
【详解】(1)a×4+b
=4a+b(千米)
答:这辆汽车行驶了(4a+b)千米。
(2)d=85,b=210时;
4×85+210
=340+210
=550(千米)
答:这辆汽车行驶了550千米。
【点睛】本题主要考查用字母表示复杂的数量关系,注意当字母表示数时,若数量关系是两部分相加减,且后面有单位,需要加上括号。
21.(1)(4x+3y)毫升
(2)900毫升
【分析】(1)用杯子的容量乘杯数即可;
(2)把x=150,y=100代入即可。
【详解】(1)2x+2x+3y=(4x+3y)毫升
答:爸爸、妈妈和东东一共倒了(4x+3y)毫升饮料。
(2)4×150+3×100
=600+300
=900(毫升)
答:他们一共倒了900毫升饮料。
【点睛】找出题目中的数量关系,是解答此题的关键。
22.(1)5(x-y)千米;(2)75千米
【分析】(1)根据路程=速度×时间,求出两车的路程,再相减即可;
(2)代入数值进行计算即可。
【详解】(1)5x-5y
=5(x-y)(千米)
答:此时甲、乙两车之间的距离5(x-y)千米。
(2)当x=80,y=65时
5(x-y)
=5×(80-65)
=5×15
=75(千米)
答:两车之间的距离是75千米。
【点睛】本题考查行程问题的计算及应用。理解题意,找出数量关系,列式计算即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
思维拓展:用字母表示数(试题)数学五年级上册苏教版
一、选择题
1.小明的爸爸今年a岁,小明今年(a-27)岁,再过3年,他们相差( )岁。
A.3 B.24 C.27 D.30
2.数a、b在直线上的位置如下图所示。下列式子中,得数最接近2的是( )。
A.a+b B.b-a C.a×b D.b÷a
3.把5(X+8)错写成了5X+8,结果比原来( )。
A.多8 B.少8 C.少32 D.多32
4.古希腊著名的毕达哥拉斯学派把1、3、6、10、15、21…这样的数称为“三角形数”,而把1、4、9、16、25、36…这样的数称为“正方形数”。从下图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻的“三角形数”之和。下列等式中,不符合这一规律的是( )。
A.25=9+16 B.36=15+21 C.49=21+28 D.64=28+36
5.用同样长的小棒摆正方形(每条边用一根小棒),照这样摆,摆n个正方形需要( )根小棒。
A.4n B.3n C.4n+2 D.3n+1
6.当三角形的三边存在下列关系:两边的平方和等于第三边的平方,我们把满足这样条件的三角形叫直角三角形。如:若32+42=52,则3、4、5可以组成一个直角三角形。下列三角形的三边能组成直角三角形的是( )。
A.2、3、4 B.6、8、9 C.5、6、7 D.5、12、13
二、填空题
7.师徒两人共同加工一批零件,徒弟每小时加工35个,师傅每小时加工a个。a-35表示( ),4小时两人共加工( )个。
8.ab都是非零自然数,且a÷b=5,则a和b的最大公因数是( ),最小公倍数是( )。
9.苗族千人长桌宴是苗族宴席的最高形式与隆重礼仪,已有几千年的历史。通常用于接亲嫁女、满月酒以及村寨联谊宴饮活动。在设定座位时如下图设计,认真观察,完成后面的问题。
(1)按照上图所示规律,安排5张桌子最多可以坐( )人。
(2)如果安排n张桌子,那么可坐人数可以用式子( )表示。
10.有8个竹筐,每个竹筐装a只小兔,一共可装( )只小兔。
11.研究人员发现,蟋蟀每分钟叫的次数与当地气温之间有如下关系:t=h÷3(t表示当地气温,h表示蟋蟀每分钟叫的次数)。如果测得蟋蟀每分钟大约叫105次,那么当地气温是( )℃;如果测得当地气温是21℃,那么此时蟋蟀每分钟大约( )次。
12.这里有一系列由小正方体搭成的塔。
下面是每个塔的平面示意图,图中的数字表示在垂直方向上有几个小正方体。
搭成“塔6”需要( )个小正方体。
三、判断题
13.等腰三角形的顶角是a°,则一个底角是180°-a°。( )
14.当时,。( )
15.9与x的8倍的和列式为(9+x)×8。( )
16.五(1)班有女生x人,男生人数是女生人数的0.4倍,五(1)班共有学生0.4x人。( )
17.方程6x+5=41与方程7.5x-27=18的解相同。( )
四、解答题
18.
图形 ……
小棒根数 6 11 16 ……
(1)照这样的摆法,摆12个这样的六边形需要多少根小棒?
(2)你能用一个式子表示出小棒的根数吗?
小棒的根数=______________。
19.图1是2021年6月的月历表。小明用如图2所示的“十字”型框图放置到月历表合适的位置上,可以框中5个数。
(1)如图1所示,若框中的5个数中,正中间的数是10,则框中5个数的和是( );
(2)若框中的5个数中,正中间的数为n,则这5个数的和为( );
(3)按照上面的框法,框中5个数的和可以是100吗?为什么?
20.有一辆汽车,每小时行驶a千米,上午行驶了4小时,下午行驶了b千米。
(1)用含有字母的式子表示这辆汽车行驶的路程。
(2)当,时,这辆汽车行驶了多少千米?
21.一个大玻璃杯可盛饮料x毫升,一个小玻璃杯可盛饮料y毫升。爸爸和妈妈各倒了2大玻璃杯饮料,东东倒了3小玻璃杯饮料。
(1)用含有字母的式子表示爸爸、妈妈和东东一共倒了多少毫升饮料。
(2)当x=150,y=100时,他们一共倒了多少毫升饮料?
22.甲车的速度是x千米/小时,乙车的速度是y千米/小时。两车同时从A地出发前往B地,5小时后甲车到达B地。
(1)用含x和y的式子表示此时甲、乙两车之间的距离。
(2)当x=80,y=65时,求两车之间的距离。
参考答案:
1.C
【分析】根据年龄差不会随时间的变化而改变,所以他们今年的年龄差就是3年后他们的年龄差。
【详解】a-(a-27)
=a-a+27
=27(岁)
小明的爸爸今年a岁,小明今年(a-27)岁,再过3年,他们相差27岁。
故答案为:C
【点睛】理解年龄差不随时间的变化而改变是解答此题的关键。
2.D
【分析】根据数a、b在数轴上的位置可知,0<a<b<1,且a接近0,b接近1;由此设a=0.4,b=0.7代入四个选项的式子中,计算出结果,再比较大小即可。
【详解】根据0<a<b<1,设a=0.4,b=0.7;
A.a+b;0.4+0.7=1.1;
B.b-a;0.7-0.4=0.3
C.a×b;0.4×0.7=0.28
D.b÷a;0.7÷0.4=1.75
1.75最接近2。
数a、b在直线上的位置如下图所示。下列式子中,得数最接近2的是b÷a。
故答案为:D
【点睛】根据a、b在数轴上的位置,用赋值法更直观地得出结论。
3.C
【分析】先运用乘法分配律把5(X+8)改写成5X+5×8;5×8-8=32,5X+8的结果比原来少32,即可解答。
【详解】5(X+8)-(5X+8)
=5X+5×8-5X-8
=40-8
=32
把5(X+8)错写成了5X+8,结果比原来少32。
故答案为:C
【点睛】本题考查含义字母的式子的化简,根据乘法分配律把5(X+8)进行改写是解题的关键。
4.A
【分析】根据“三角形数”的规律是:1,3,6,10,15,21,28,36,45…,而“正方形数”是两个相邻“三角形数”之和,据此逐项判断即可。
【详解】A.25=9+16;25=52,是正方形数,9和16不是三角形数,不符合规律,符合题意;
B.36=15+21;36=62,是正方形数,15和21是相邻的三角形数,符合规律,不符合题意;
C.49=21+28;49=72,是正方形数,21和28是相邻的三角形数,符合规律,不符合题意;
D.64=28+36;64=82,是正方形数,28和36是相邻的三角形数,符合规律,不符合题意。
故答案为:A
【点睛】解答本题的关键是找清楚“三角形数”和“正方形数”的关系,从而进行求解。
5.D
【分析】根据图,摆1个正方形需要4根小棒,摆2个正方形需要(4+3)根小棒,摆3个正方形需要(4+3+3)根小棒,由此可得摆n个正方形需要小棒数量为:4+(n-1)×3,根据答题。
【详解】由分析可得:
摆1个正方形需要:4根小棒;
摆2个正方形需要:4+3=7(根)
摆2个正方形需要:4+3+3=10(根)
……
摆n个正方形需要:
4+(n-1)×3
=4+3n-3
=(3n+1)根
故答案为:D
【点睛】解决本题的关键通过观察给出的图片,找出图片之间的数量关系,得出规律,再根据规律去解决问题。
6.D
【分析】根据题意可知,在直角三角形内,两条直角边的平方和等于斜边的平方,据此计算每个选项是否符合即可。
【详解】A.22+32
=4+9
=13
42=16
13≠16
2、3、4不能组成直角三角形;
B.62+82
=36+64
=100
92=81
100≠81
6、8、9不能组成直角三角形;
C.52+62
=25+36
=61
72=49
61≠49
5、6、7不能组成直角三角形;
D.52+122
=25+144
=169
132=169
169≠169
5、12、13能组成直角三角形。
故答案为:D
【点睛】本题主要考查了直角三角形的认识以及三边关系的应用。
7. 师傅比徒弟每小时多加工多少个 4a+140
【分析】由题意得a-35表示师傅比徒弟每小时多加工多少个;两人1小时共加工(a+35)个,乘4就是4小时共加工的个数。
【详解】a-35表示师傅比徒弟每小时多加工多少个,4小时两人共加工:(4a+140)个。
【点睛】此题考查了用字母表示数的方法,关键是弄清题中字母所表示的意义,再进一步解答。
8. b a
【详解】略
【分析】明确a是b的倍数,b是a的因数。则a,b两数的最大公因数是b,最小公倍数是a。
9.(1)22
(2)4n+2
【分析】(1)观察图形可知,安排1张桌子,可坐6人;安排2张桌子,可坐10人;安排3张桌子,可坐14人……发现:每增加一张桌子,可坐的人数增加4人,据此得出安排5张桌子最多可以坐的人数。
(2)由上一题,可得出:6=4×1+2,10=4×2+2,14=4×3+2……,据此找到规律,并按规律解答。
【详解】(1)安排1张桌子,可坐6人;
安排2张桌子,可坐6+4=10(人);
安排3张桌子,可坐10+4=14(人);
安排4张桌子,可坐14+4=18(人);
安排5张桌子,可坐18+4=22(人);
按照上图所示规律,安排5张桌子最多可以坐22人。
(2)安排1张桌子,可坐6人,6=4×1+2;
安排2张桌子,可坐10人,10=4×2+2;
安排3张桌子,可坐14人,14=4×3+2;
……
如果安排n张桌子,那么可坐人数可以用式子(4n+2)表示。
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
10.8a
【解析】略
11. 35 63
【分析】由题意得,蟋蟀每分钟大约叫105次,即h=105,求t的值;如果测得当地气温是21℃,即t=21,求h的值。
【详解】当h=105时,
t=105÷3
=35(℃);
当t=21时,
h=21×3
=63(次)
研究人员发现,蟋蟀每分钟叫的次数与当地气温之间有如下关系:t=h÷3(t表示当地气温,h表示蟋蟀每分钟叫的次数)。如果测得蟋蟀每分钟大约叫105次,那么当地气温是35℃;如果测得当地气温是21℃,那么此时蟋蟀每分钟大约63次。
【点睛】掌握用字母表示数的意义是解题关键。
12.56
【分析】第一个塔有1个小正方体,第二个塔有(2+1×2)个小正方体,第三个塔有(3+2×2+1×3)个小正方体,第四个塔有(4+3×2+2×3+1×4)个小正方体,则第五个塔有(5+4×2+3×3+2×4+1×5)个小正方体,第六个塔有(6+5×2+4×3+3×4+2×5+1×6)个小正方体。
【详解】6+5×2+4×3+3×4+2×5+1×6
=6+10+12+12+10+6
=16+12+12+10+6
=28+12+10+16
=40+10+6
=50+6
=56(个)
搭成“塔6”需要(56)个小正方体。
【点睛】本题主要考查数与形结合的规律,关键是根据所给图示,找出规律,并根据规律解题。
13.×
【分析】三角形内角和是180°,等腰三角形的有2个相等的底角和1个顶角,据此可知:等腰三角形的一个底角=(180°-顶角)÷2,据此解答。
【详解】(180°-a°)÷2
等腰三角形的顶角是a°,则一个底角是(180°-a°)÷2。
原题干说法错误。
故答案为:×
【点睛】掌握三角形内角和、等腰三角形的特征以及字母表示数的方法是解答本题的关键。
14.×
【分析】把代入计算,观察结果是否等于47即可。
【详解】把代入中,
=
=
=
当时,。原题干说法错误。
故答案为:×
【点睛】本题主要考查了含未知数式子的求值,把x的值代入式子计算即可。
15.×
【分析】先用x乘8,求出x的8倍,然后再加上9,然后与原题中的式子作比较即可判断。
【详解】9与x的8倍的和列式为:
9+x×8=9+8x
(9+x)×8=9×8+8x=72+8x
72+8x=9+8x
所以题干说法错误。
故答案为:×
【点睛】本题考查了字母表示数,要分清楚数量之间的关系,先求什么再求什么,找清列式的顺序,列出算式或方程计算。
16.×
【分析】根据题意,先求出五(1)班的男生人数,也就是求女生x人的0.4倍是多少,进而再加上女生人数,就是五(1)班全班人数。
【详解】x+x×0.4
=x+0.4x
=1.4x(人)
即五(1)班共有学生 1.4x人,所以原题答案错误。
故答案为:×
【点睛】此题考查用字母表示数,关键是用含字母的式子表示出男生人数,再加上女生人数得解。
17.√
【分析】利用等式的性质求出两个方程的解,看两个解是否相同即可。
【详解】6x+5=41
解:6x+5-5=41-5
6x÷6=36÷6
x=6
7.5x-27=18
解:7.5x-27+27=18+27
7.5x÷7.5=45÷7.5
x=6
方程6x+5=41与方程7.5x-27=18的解相同。
原题说法正确。
故答案为:√
【点睛】本题考查了方程的解法,解题过程要利用等式的性质。
18.(1)50根;(2)2+4n(n表示第n个图形)
【分析】观察图形以及其小棒根数可知:
摆第1个图形需要(2+4×1)根小棒;
摆第2个图形需要(2+4×2)根小棒;
摆第3个图形需要(2+4×3)根小棒;
以此类推
……
摆第12个图形需要(2+4×12)根小棒;
……
摆第n个图形需要(2+4n)根小棒。
【详解】(1)2+4×12
=2+48
=50(根)
答:需要50根小棒。
(2)小棒的根数=2+4n(n表示第n个图形)(答案不唯一)
用式子表示为小棒的根数=2+4n(n表示第n个图形)。
【点睛】本题的关键是要找到图形的小棒根数变化部分的共同点,以此推断出其规律。
19.(1)50;
(2)5n;
(3)不可以;理由见详解
【分析】(1)当正中间的数为10时,框中的5个数分别为3、10、17、9、11,用加法求出这个5个数的和;
(2)当正中间的数为n时,n上面的数为(n-7),n下面的数为(n+7),n左面的数为(n-1),n右面的数为(n+1),用含有n的式子表示出这5个数的和;
(3)正中间的数为框中这5个数的平均数,根据这5个数的和为100求出正中间的数,根据正中间的数确定其它4个数是否存在,据此解答。
【详解】(1)
3+9+10+11+17
=12+10+11+17
=22+11+17
=33+17
=50
所以,框中5个数的和是50。
(2)n-7+n+7+n-1+n+1+n
=n+n+n+n+n-7+7-1+1
=(n+n+n+n+n)-(7-7+1-1)
=5n
所以,这5个数的和为5n。
(3)100÷5=20
由上可知,框中5个数的和不可以是100,因为框中5个数的和为100时,正中间的数为20,但月历表中20的右面没有数字。
【点睛】月历表中上下相邻两个数的差是7,左右相邻两个数的差是1,根据框中的数与数之间的关系,用正中间的数表示出其它4个数是解答题目的关键。
20.(1)()千米
(2)550千米
【分析】(1)根据路程=速度×时间;用a×4,求出上午行驶的路程,再加上下午行驶的路程,即可求出这辆汽车行驶的路程;
(2)当a=85,b=210时,代入(1),求出结果即可。
【详解】(1)a×4+b
=4a+b(千米)
答:这辆汽车行驶了(4a+b)千米。
(2)d=85,b=210时;
4×85+210
=340+210
=550(千米)
答:这辆汽车行驶了550千米。
【点睛】本题主要考查用字母表示复杂的数量关系,注意当字母表示数时,若数量关系是两部分相加减,且后面有单位,需要加上括号。
21.(1)(4x+3y)毫升
(2)900毫升
【分析】(1)用杯子的容量乘杯数即可;
(2)把x=150,y=100代入即可。
【详解】(1)2x+2x+3y=(4x+3y)毫升
答:爸爸、妈妈和东东一共倒了(4x+3y)毫升饮料。
(2)4×150+3×100
=600+300
=900(毫升)
答:他们一共倒了900毫升饮料。
【点睛】找出题目中的数量关系,是解答此题的关键。
22.(1)5(x-y)千米;(2)75千米
【分析】(1)根据路程=速度×时间,求出两车的路程,再相减即可;
(2)代入数值进行计算即可。
【详解】(1)5x-5y
=5(x-y)(千米)
答:此时甲、乙两车之间的距离5(x-y)千米。
(2)当x=80,y=65时
5(x-y)
=5×(80-65)
=5×15
=75(千米)
答:两车之间的距离是75千米。
【点睛】本题考查行程问题的计算及应用。理解题意,找出数量关系,列式计算即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
