实际问题与二次函数(3)(河北省秦皇岛市)
文档属性
| 名称 | 实际问题与二次函数(3)(河北省秦皇岛市) |  | |
| 格式 | rar | ||
| 文件大小 | 52.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-15 19:05:00 | ||
图片预览


文档简介
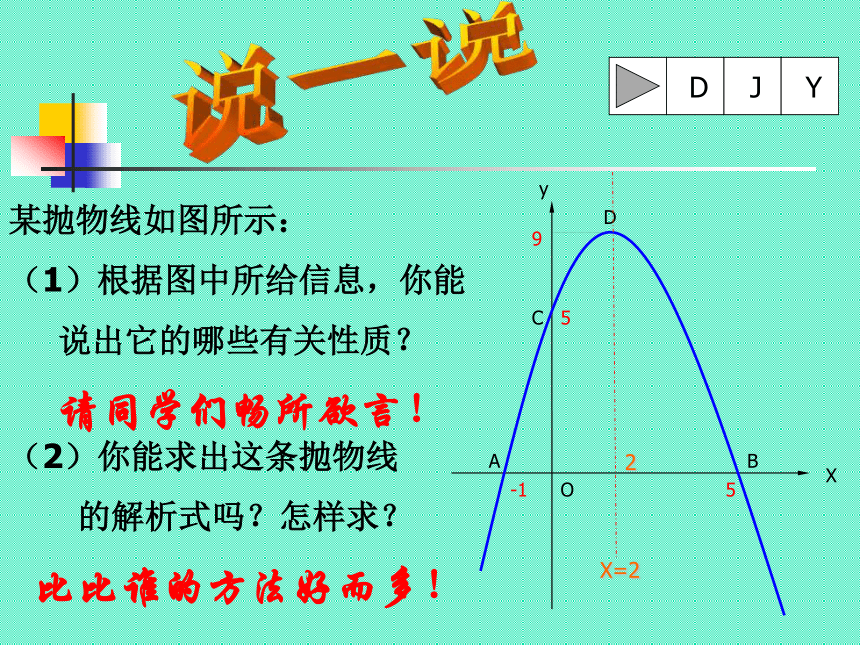
课件19张PPT。生活中的抛物线——二次函数应用(一)说一说某抛物线如图所示:
(1)根据图中所给信息,你能
说出它的哪些有关性质?
请同学们畅所欲言!
(2)你能求出这条抛物线
的解析式吗?怎样求?
比比谁的方法好而多!解:
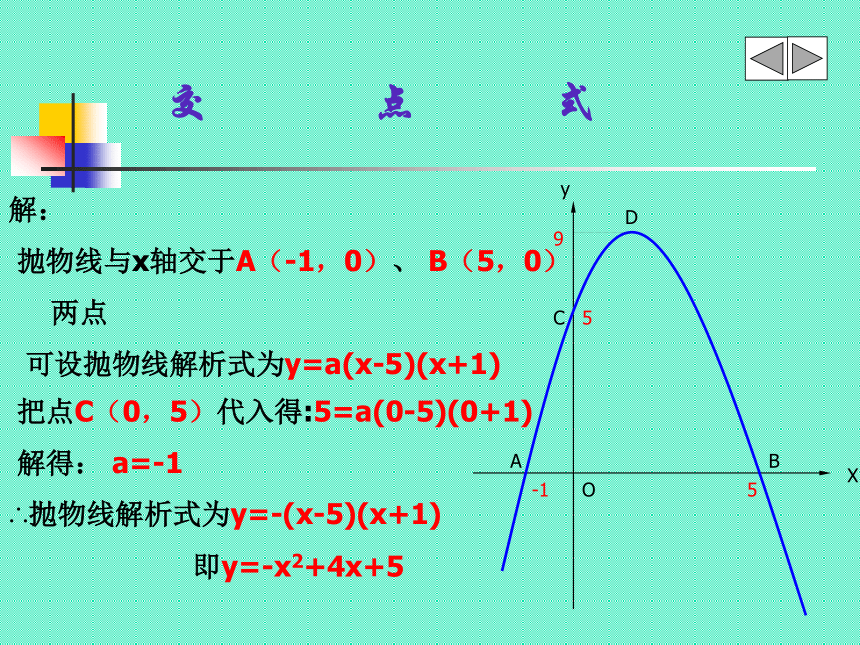
抛物线与x轴交于A(-1,0)、 B(5,0)
两点
可设抛物线解析式为y=a(x-5)(x+1)
交 点 式
把点C(0,5)代入得:5=a(0-5)(0+1)
解得: a=-1
∴抛物线解析式为y=-(x-5)(x+1)
即y=-x2+4x+5
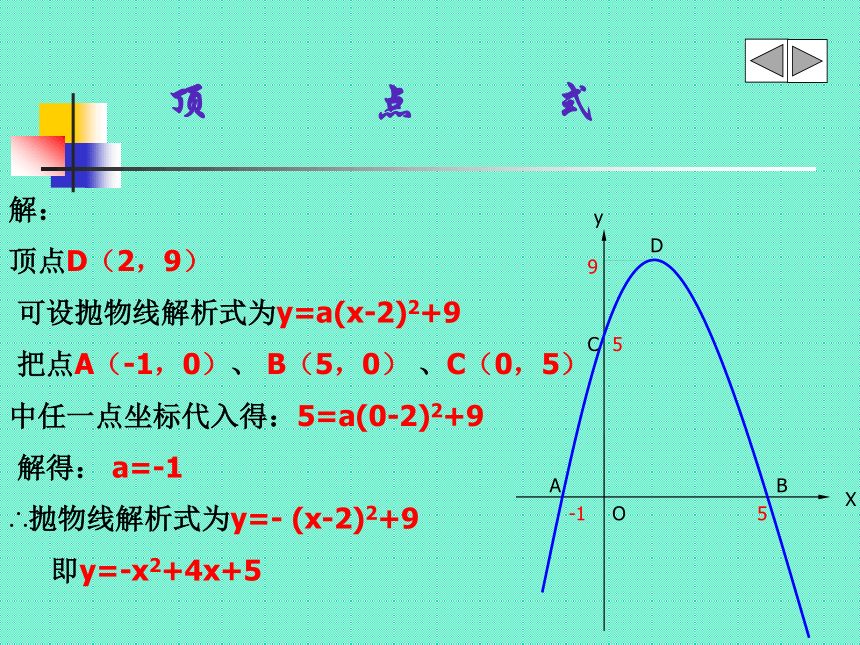
解:
顶点D(2,9)
可设抛物线解析式为y=a(x-2)2+9
把点A(-1,0)、 B(5,0) 、C(0,5)
中任一点坐标代入得:5=a(0-2)2+9
解得: a=-1
∴抛物线解析式为y=- (x-2)2+9
即y=-x2+4x+5
顶 点 式解:
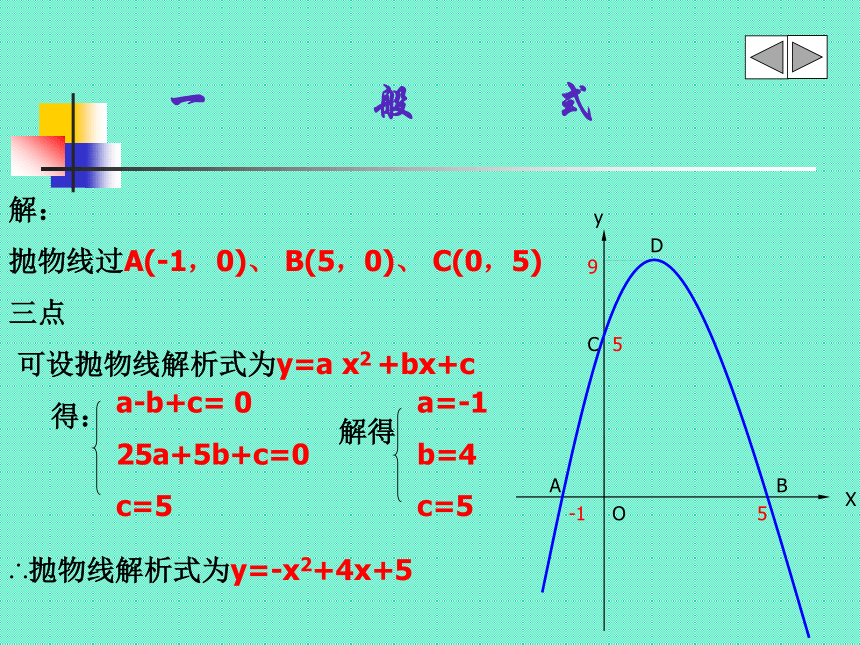
抛物线过A(-1,0)、 B(5,0)、 C(0,5)
三点
可设抛物线解析式为y=a x2 +bx+c
得:
∴抛物线解析式为y=-x2+4x+5
一 般 式a-b+c= 0
25a+5b+c=0
c=5 a=-1
b=4
c=5解得掌握规律
活用方法
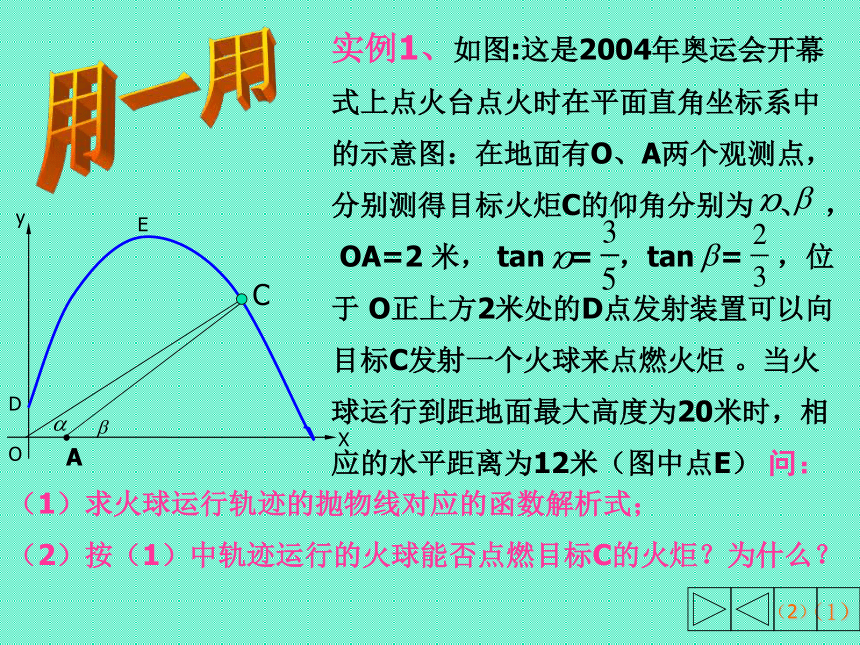
提高效率(1)(2)用一用实例1、如图:这是2004年奥运会开幕
式上点火台点火时在平面直角坐标系中
的示意图:在地面有O、A两个观测点,
分别测得目标火炬C的仰角分别为 、 ,
OA=2 米, tan = ,tan = ,位
于 O正上方2米处的D点发射装置可以向
目标C发射一个火球来点燃火炬 。当火
球运行到距地面最大高度为20米时,相
应的水平距离为12米(图中点E) 问:
(1)求火球运行轨迹的抛物线对应的函数解析式;
(2)按(1)中轨迹运行的火球能否点燃目标C的火炬?为什么? ∵抛物线过点D(0,2)
∴可得:2=a(0-12)2+20
解得: a=
∴ 火球运行轨迹的抛物线解析式为y= (x-12)2+20
C(2)(12,20)能否用一般式或交点式解这个问题? 解(1)由题意得,抛物线的顶点E(12,20)
可设抛物线解析式为y=a(x-12)2+20
∴点C(20,12)在火球运行轨迹的抛物线上
∴按(1)中轨迹运行的火球能点燃目标C的火炬。(1)FC∵ tan = ,tan =
∴解得: , ∴C(20,12)
把x=20代入抛物线解析式得y= (20-12)2+20=12=
解(2)过点C作CF⊥X轴,垂足为F设C( , )
想一想 在解决了上例问题
后,你能用上例的抛物
线再创设一个情景,编
一道类似的实际问题吗?
请试试看!
B在生活中,抛物线有着很大的实际应用价值。解决这类实际问题时,首要的一步就是_______________,而这一步必须把抛物线建立在特定的 _____________中才能顺利进行。否则,将寸步难行!
你得到了什么启示?求出抛物线解析式直角坐标系也是抛物线形的生活中有许多桥你知道吗?试一试AB
实例2、如图:有一座抛物线形的石拱桥,在正常水位时水面AB
的宽为20米;当水位上升3米时,水面CD的宽为10米.
(1)求这座抛物线桥拱的高(即桥拱的最高点离水面AB的距离).
(2)当水面位于CD时,恰好有一宽4米、高0.8米的货船从桥下
经过,问:这艘船能否安全通过桥拱?为什么?
(2)(1) 解 :(1)如图:以AB所在直线为x轴,AB的中垂线为y轴建立直角坐标系
(2)试一试AB 解 (2)如图:由题意得:OP=GI=2米,PM=PI+IM=3+0.8=3.8米
设 Q(x,y) 则x =OP=2 将其代入抛物线解析式,得:试一试AB ∴ 这艘船能安全通过桥拱。
(1)想一想 本例中如果建立直角坐标系的方法不同,那么所求得的抛物线解析式是否相同?这对题中各个实际问题的解决有影响吗?
请大家课后去尝试探索一下!
回顾小结抛物线应用的基本步骤:
1、建立适当的直角坐标系;
2、在所建立的直角坐标系中求出抛物线的解析式;
3、利用抛物线上的点的坐标与函数解析式的关系,点的横、纵坐标在坐标系中的几何意义以及二次函数的有关性质等去解决所求的实际问题。
课后实践1)将“实例2”用另一种不同的建立坐标系的方法来解决;
2)平时我们跳大绳时,绳甩到最高处的形状可以近似地看为抛物线。如图所示,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙、丁分别站在距甲拿绳的手水平距离1米、2.5米处,绳子在甩到最高处时刚好通过他们的头顶。已知学生丙的身高是1.5米,求学生丁的身高?谢谢大家
再见!嘉兴市清河中学
初三数学组
制作:陈豪
2005年3月敬请各位老师指导!
(1)根据图中所给信息,你能
说出它的哪些有关性质?
请同学们畅所欲言!
(2)你能求出这条抛物线
的解析式吗?怎样求?
比比谁的方法好而多!解:
抛物线与x轴交于A(-1,0)、 B(5,0)
两点
可设抛物线解析式为y=a(x-5)(x+1)
交 点 式
把点C(0,5)代入得:5=a(0-5)(0+1)
解得: a=-1
∴抛物线解析式为y=-(x-5)(x+1)
即y=-x2+4x+5
解:
顶点D(2,9)
可设抛物线解析式为y=a(x-2)2+9
把点A(-1,0)、 B(5,0) 、C(0,5)
中任一点坐标代入得:5=a(0-2)2+9
解得: a=-1
∴抛物线解析式为y=- (x-2)2+9
即y=-x2+4x+5
顶 点 式解:
抛物线过A(-1,0)、 B(5,0)、 C(0,5)
三点
可设抛物线解析式为y=a x2 +bx+c
得:
∴抛物线解析式为y=-x2+4x+5
一 般 式a-b+c= 0
25a+5b+c=0
c=5 a=-1
b=4
c=5解得掌握规律
活用方法
提高效率(1)(2)用一用实例1、如图:这是2004年奥运会开幕
式上点火台点火时在平面直角坐标系中
的示意图:在地面有O、A两个观测点,
分别测得目标火炬C的仰角分别为 、 ,
OA=2 米, tan = ,tan = ,位
于 O正上方2米处的D点发射装置可以向
目标C发射一个火球来点燃火炬 。当火
球运行到距地面最大高度为20米时,相
应的水平距离为12米(图中点E) 问:
(1)求火球运行轨迹的抛物线对应的函数解析式;
(2)按(1)中轨迹运行的火球能否点燃目标C的火炬?为什么? ∵抛物线过点D(0,2)
∴可得:2=a(0-12)2+20
解得: a=
∴ 火球运行轨迹的抛物线解析式为y= (x-12)2+20
C(2)(12,20)能否用一般式或交点式解这个问题? 解(1)由题意得,抛物线的顶点E(12,20)
可设抛物线解析式为y=a(x-12)2+20
∴点C(20,12)在火球运行轨迹的抛物线上
∴按(1)中轨迹运行的火球能点燃目标C的火炬。(1)FC∵ tan = ,tan =
∴解得: , ∴C(20,12)
把x=20代入抛物线解析式得y= (20-12)2+20=12=
解(2)过点C作CF⊥X轴,垂足为F设C( , )
想一想 在解决了上例问题
后,你能用上例的抛物
线再创设一个情景,编
一道类似的实际问题吗?
请试试看!
B在生活中,抛物线有着很大的实际应用价值。解决这类实际问题时,首要的一步就是_______________,而这一步必须把抛物线建立在特定的 _____________中才能顺利进行。否则,将寸步难行!
你得到了什么启示?求出抛物线解析式直角坐标系也是抛物线形的生活中有许多桥你知道吗?试一试AB
实例2、如图:有一座抛物线形的石拱桥,在正常水位时水面AB
的宽为20米;当水位上升3米时,水面CD的宽为10米.
(1)求这座抛物线桥拱的高(即桥拱的最高点离水面AB的距离).
(2)当水面位于CD时,恰好有一宽4米、高0.8米的货船从桥下
经过,问:这艘船能否安全通过桥拱?为什么?
(2)(1) 解 :(1)如图:以AB所在直线为x轴,AB的中垂线为y轴建立直角坐标系
(2)试一试AB 解 (2)如图:由题意得:OP=GI=2米,PM=PI+IM=3+0.8=3.8米
设 Q(x,y) 则x =OP=2 将其代入抛物线解析式,得:试一试AB ∴ 这艘船能安全通过桥拱。
(1)想一想 本例中如果建立直角坐标系的方法不同,那么所求得的抛物线解析式是否相同?这对题中各个实际问题的解决有影响吗?
请大家课后去尝试探索一下!
回顾小结抛物线应用的基本步骤:
1、建立适当的直角坐标系;
2、在所建立的直角坐标系中求出抛物线的解析式;
3、利用抛物线上的点的坐标与函数解析式的关系,点的横、纵坐标在坐标系中的几何意义以及二次函数的有关性质等去解决所求的实际问题。
课后实践1)将“实例2”用另一种不同的建立坐标系的方法来解决;
2)平时我们跳大绳时,绳甩到最高处的形状可以近似地看为抛物线。如图所示,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙、丁分别站在距甲拿绳的手水平距离1米、2.5米处,绳子在甩到最高处时刚好通过他们的头顶。已知学生丙的身高是1.5米,求学生丁的身高?谢谢大家
再见!嘉兴市清河中学
初三数学组
制作:陈豪
2005年3月敬请各位老师指导!
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
