11.1.2第2课时 三角形的高、中线与角平分线 课件(19张PPT)
文档属性
| 名称 | 11.1.2第2课时 三角形的高、中线与角平分线 课件(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
人教版八年级上册
第十一章 三角形
第2课时 三角形的高、中线与角平分线
01
知识重点
02
对点范例
03
典型例题
04
举一反三
(1)定义:从三角形的一个顶点向它的对边所在直线作______,顶点和垂足之间的线段叫做三角形的______.
(2)性质:三角形的三条高所在的直线交于______点.锐角三角形三条高的交点在三角形的______,直角三角形三条高的交点在__________,钝角三角形三条高的交点在三角形的______.
知识点一:三角形的高
垂线
高
一
内部
直角顶点
外部
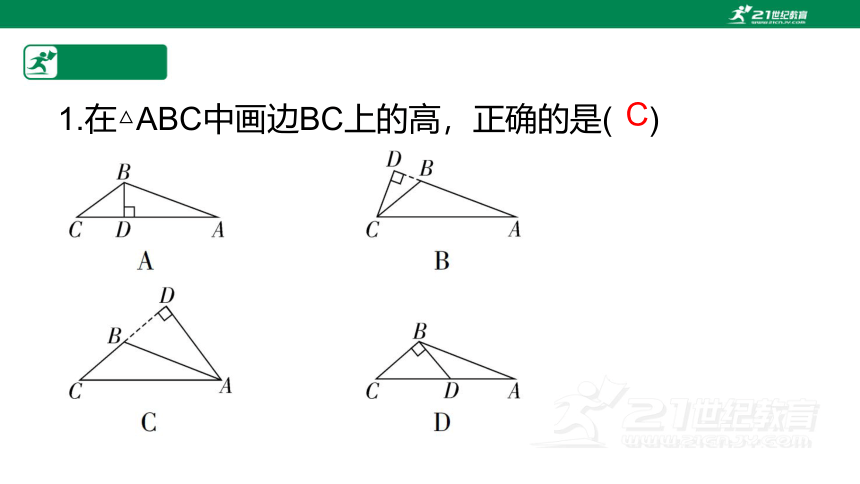
1.在△ABC中画边BC上的高,正确的是( )
C
(1)定义:在三角形中,连接三角形的顶点与________的线段叫做三角形的中线.
注意:任意三角形都有_____条中线,并相
交于同一点,这个点叫做三角形的______.
(2)性质:如图11-2-1,AD是△ABC的中线,
则______=______=______.
知识点二:三角形的中线
对边中点
三
重心
BD
DC
BC
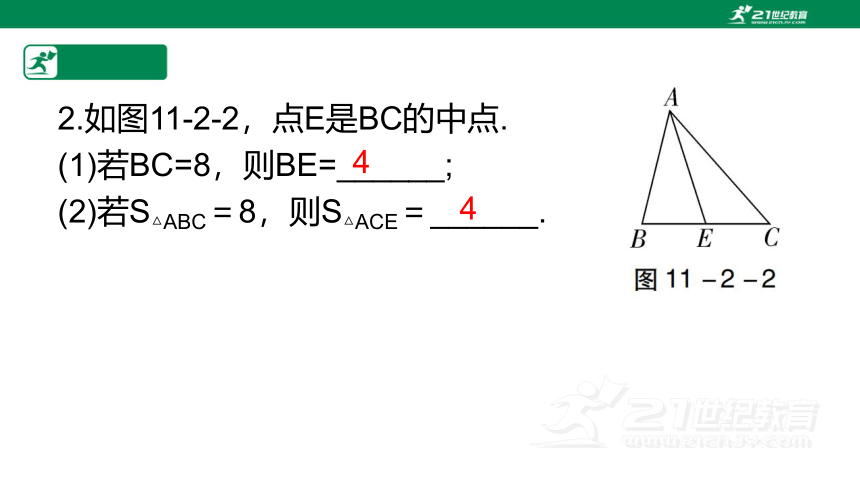
2.如图11-2-2,点E是BC的中点.
(1)若BC=8,则BE=______;
(2)若S△ABC=8,则S△ACE=______.
4
4
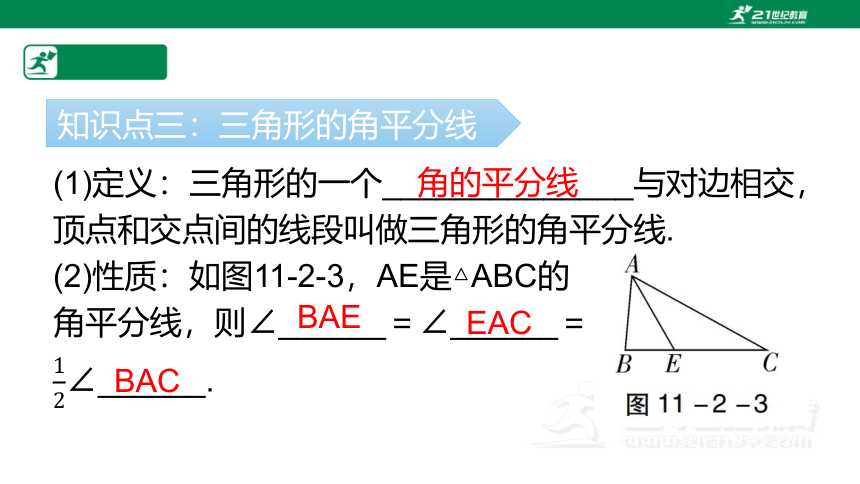
(1)定义:三角形的一个______________与对边相交,顶点和交点间的线段叫做三角形的角平分线.
(2)性质:如图11-2-3,AE是△ABC的
角平分线,则∠______=∠______=
∠______.
知识点三:三角形的角平分线
角的平分线
BAE
EAC
BAC
3.如图11-2-4,AD是△ABC的角平分线,则( )
A.∠1=∠BAC
B.∠1=∠ABC
C.∠1=∠BAC
D.∠1=∠ABC
A
【例1】如图11-2-5,△ABC的边BC上的高为AD,且BC=9 cm,AD=2 cm,AB=6 cm.
(1)画出△ABC在AB边上的高CE;
(2)CE的长为______.
思路点拨:(1)根据三角形高的定义作高;(2)利用等面积法求三角形的高.
3 cm
解:(1)如答图11-2-1,CE即为所作.
4.如图11-2-6,在△ABC中,AB=15,BC=20.
(1)画出△ABC的高AD和CE;
(2)若AD=3,则CE的长为______.
4
解:(1)如答图11-2-2,AD,CE即为所作.
【例2】(无图题)已知AD是△ABC的中线,且△ABD的周长比△ACD的周长多4 cm.若AB=16 cm,则AC=______ cm.
思路点拨:利用三角形中线的性质解决问题即可.
12
5.如图11-2-7,点D,E分别是BC,AD的中点,若S△ABD=8,则S△ACE=______.
4
【例3】如图11-2-8,在△ABC中,CE平分
∠ACB,AD∥EC,交BC的延长线于点D,若
∠CAD=60°,求∠BCA的度数.
思路点拨:由角平分线的性质和平行线的性质可求解.
解:∵AD∥EC,∠CAD=60°,
∴∠ACE=60°.
又∵CE平分∠ACB,
∴∠ACB=2∠ACE=120°.
6.如图11-2-9,在△ABC中,CE平分∠ACB,CE⊥AB,ED∥AC,DF⊥AB.若∠ACE=40°,求∠EDC的度数.
解:∵CE平分∠ACB,∠ACE=40°,
∴∠ACB=80°.
又∵AC∥DE,
∴∠ACB+∠CDE=180°.
∴∠EDC=100°.
【例4】如图11-2-10,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于点E,F为AB上一点,CF⊥AD于点H.下列判断正确的是( )
A.AD是△ABE的角平分线
B.BE是△ABD的边AD上的中线
C.CH是△ACD的边AD上的高
D.AH是△ABC的角平分线和高
思路点拨:透彻理解三角形的高、中线、角平分线的定义是解题关键.
C
7.(提升题)如图11-2-11,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法中:①S△ABE=S△BCE;②∠ABD=∠CAD;③∠BAD=2∠ACF;④AF=FB.正确的是( )
A.①②③④ B.①②④
C.①②③ D.③④
C
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版八年级上册
第十一章 三角形
第2课时 三角形的高、中线与角平分线
01
知识重点
02
对点范例
03
典型例题
04
举一反三
(1)定义:从三角形的一个顶点向它的对边所在直线作______,顶点和垂足之间的线段叫做三角形的______.
(2)性质:三角形的三条高所在的直线交于______点.锐角三角形三条高的交点在三角形的______,直角三角形三条高的交点在__________,钝角三角形三条高的交点在三角形的______.
知识点一:三角形的高
垂线
高
一
内部
直角顶点
外部
1.在△ABC中画边BC上的高,正确的是( )
C
(1)定义:在三角形中,连接三角形的顶点与________的线段叫做三角形的中线.
注意:任意三角形都有_____条中线,并相
交于同一点,这个点叫做三角形的______.
(2)性质:如图11-2-1,AD是△ABC的中线,
则______=______=______.
知识点二:三角形的中线
对边中点
三
重心
BD
DC
BC
2.如图11-2-2,点E是BC的中点.
(1)若BC=8,则BE=______;
(2)若S△ABC=8,则S△ACE=______.
4
4
(1)定义:三角形的一个______________与对边相交,顶点和交点间的线段叫做三角形的角平分线.
(2)性质:如图11-2-3,AE是△ABC的
角平分线,则∠______=∠______=
∠______.
知识点三:三角形的角平分线
角的平分线
BAE
EAC
BAC
3.如图11-2-4,AD是△ABC的角平分线,则( )
A.∠1=∠BAC
B.∠1=∠ABC
C.∠1=∠BAC
D.∠1=∠ABC
A
【例1】如图11-2-5,△ABC的边BC上的高为AD,且BC=9 cm,AD=2 cm,AB=6 cm.
(1)画出△ABC在AB边上的高CE;
(2)CE的长为______.
思路点拨:(1)根据三角形高的定义作高;(2)利用等面积法求三角形的高.
3 cm
解:(1)如答图11-2-1,CE即为所作.
4.如图11-2-6,在△ABC中,AB=15,BC=20.
(1)画出△ABC的高AD和CE;
(2)若AD=3,则CE的长为______.
4
解:(1)如答图11-2-2,AD,CE即为所作.
【例2】(无图题)已知AD是△ABC的中线,且△ABD的周长比△ACD的周长多4 cm.若AB=16 cm,则AC=______ cm.
思路点拨:利用三角形中线的性质解决问题即可.
12
5.如图11-2-7,点D,E分别是BC,AD的中点,若S△ABD=8,则S△ACE=______.
4
【例3】如图11-2-8,在△ABC中,CE平分
∠ACB,AD∥EC,交BC的延长线于点D,若
∠CAD=60°,求∠BCA的度数.
思路点拨:由角平分线的性质和平行线的性质可求解.
解:∵AD∥EC,∠CAD=60°,
∴∠ACE=60°.
又∵CE平分∠ACB,
∴∠ACB=2∠ACE=120°.
6.如图11-2-9,在△ABC中,CE平分∠ACB,CE⊥AB,ED∥AC,DF⊥AB.若∠ACE=40°,求∠EDC的度数.
解:∵CE平分∠ACB,∠ACE=40°,
∴∠ACB=80°.
又∵AC∥DE,
∴∠ACB+∠CDE=180°.
∴∠EDC=100°.
【例4】如图11-2-10,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于点E,F为AB上一点,CF⊥AD于点H.下列判断正确的是( )
A.AD是△ABE的角平分线
B.BE是△ABD的边AD上的中线
C.CH是△ACD的边AD上的高
D.AH是△ABC的角平分线和高
思路点拨:透彻理解三角形的高、中线、角平分线的定义是解题关键.
C
7.(提升题)如图11-2-11,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法中:①S△ABE=S△BCE;②∠ABD=∠CAD;③∠BAD=2∠ACF;④AF=FB.正确的是( )
A.①②③④ B.①②④
C.①②③ D.③④
C
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
