人教版小学数学四年级上册3.4《角的分类》教案
文档属性
| 名称 | 人教版小学数学四年级上册3.4《角的分类》教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-15 13:18:14 | ||
图片预览


文档简介
《角的分类》教学设计
备教材内容
1.本节课教学内容是角的分类,角的分类是第二学段“图形与几何”领域中的重要内容。
2.通过测量,让学生知道直角等于90°,从而使学生进一步认识直角,即从直观认识过渡到利用度数来定义。类似,对锐角、钝角的认识也需要上升到数学层面的抽象,即用度数范围来定义这两种角。对平角和周角的编排,教材是从动态的角度引出的,这更有利于学生对“角”的相关知识作系统认识。关于角的分类的编排,其重点在于结合分的过程对这几种角的特征作进一步的确认,特别是对锐角和钝角的再认识。此外,还要求学生去探索周角、平角和直角之间在度数方面的倍数关系。
3.教材先设计测量活动,让学生知道直角等于90°,从直观认知过渡到利用度数来定义直角,再通过两把折扇的实物图,让学生直观地理解平角、周角的概念,并且区别它们与直线、射线的关系,最后结合分类的过程进一步学习锐角、直角、钝角、平角、周角这几种角的特征,明确周角、平角和直角之间在度数方面的倍数关系。
4.角的分类是在学生已经初步认识直线、线段、射线、角以及会用量角器量角的基础上进行教学的。学习本节课的知识,可以学会根据各种角的度数及相互关系计算出指定角的度数,为后面的平面几何的学习作铺垫。
备教法学法
学生以前对锐角、钝角和直角已有直观层面的认识,所以在教学过程中,以研究直角作为教学的突破口,先让学生找出三角尺上的直角,用量角器测量,确认直角是90°,再动态演示直角的形成过程,然后呈现一些比90°大和比90°小的角,体会钝角和锐角的形成过程。当学生对钝角、直角、锐角有了抽象认识之后,再通过呈现扇子的形状抽象出平角和周角的形成过程,明确两者的概念。教学中,充分借助多媒体教学手段动态演示这五种角的形成过程,帮助学生理解不同角之间的关系。在学习过程中,学生通过量直角,画平角、周角,深刻体会它们的特征。以直角为突破口。学生以前对锐角、钝角和直角已有直观层面的认识,所以,以研究直角作为教学的突破口比较合理。教学中,可设计三个层次的活动:①测量三角尺上各个角的度数,确认直角为90°;②动态演示直角的形成过程,即一条射线绕着端点旋转90°后形成的图形;③呈现一些比90°大和比90°小的角,体会一定度数的钝角和锐角的形成过程。然后引出对180°的角(平角)和360°的角(周角)的认识。这样,可将5类角的关系建立在一个动态过程中来认识,有利于学生理解不同角之间的关系。加强操作,积累活动经验。活动可设计成两类:①度量和画一些特定度数的角,如量直角,画平角、周角,确认它
们的特点;②操作活动角去体会、想象、表征角的大小关系。特别在教学例2时,让学生摆
出不同的角,体会不同角的度数差异,并关注两个难点的处理:一是体会周角与0°角的区别;二是锐角和钝角的度数范围理解。
备已学知识
1.初步认识了钝角、直角、锐角,知道三者之间的关系:锐角<直角<钝角。
2.会用三角尺或直观观察判断出某一个角是锐角、直角还是钝角。
3.掌握了角的测量方法:把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合,角的另一边所对的量角器上的刻度就是这个角的度数。
备教学目标
1. 知道1 直角=90°、1 平角=180°、1 周角=360°,以及钝角与锐角的度数范围,了解这几种角的大小关系。
2. 经历动态认识各种角的形成过程,结合角的度数建构起各种角的概念表象,完成从直观到
抽象的认知过程。
3. 在学习过程中,培养探究意识,积累丰富的数学活动经验。
备教学重难点
重点:认识平角、周角,掌握锐角、直角、钝角、平角、周角之间的关系。引导学生能按一种合理的标准对角进行分类。
难点:周角是教学中的一个难点,因为周角比较特殊,角的两条边重合,教学时,我拿出活动角使学生看清把活动角旋转了一圈,然后,小结出周角的定义,让学生观察周角的画法,指指周角的顶点和两条边,从而明确周角的两条边重合在一起。
备知识讲解
知识点一 认识平角和周角
问题导入 我们已经认识了锐角、直角和钝角,你知道直角是多少度吗?你还认识其他的角吗?它们又有哪些特征呢?(教材42页)
过程讲解
1.明确直角的度数和角的形成过程
(1)明确直角的度数。
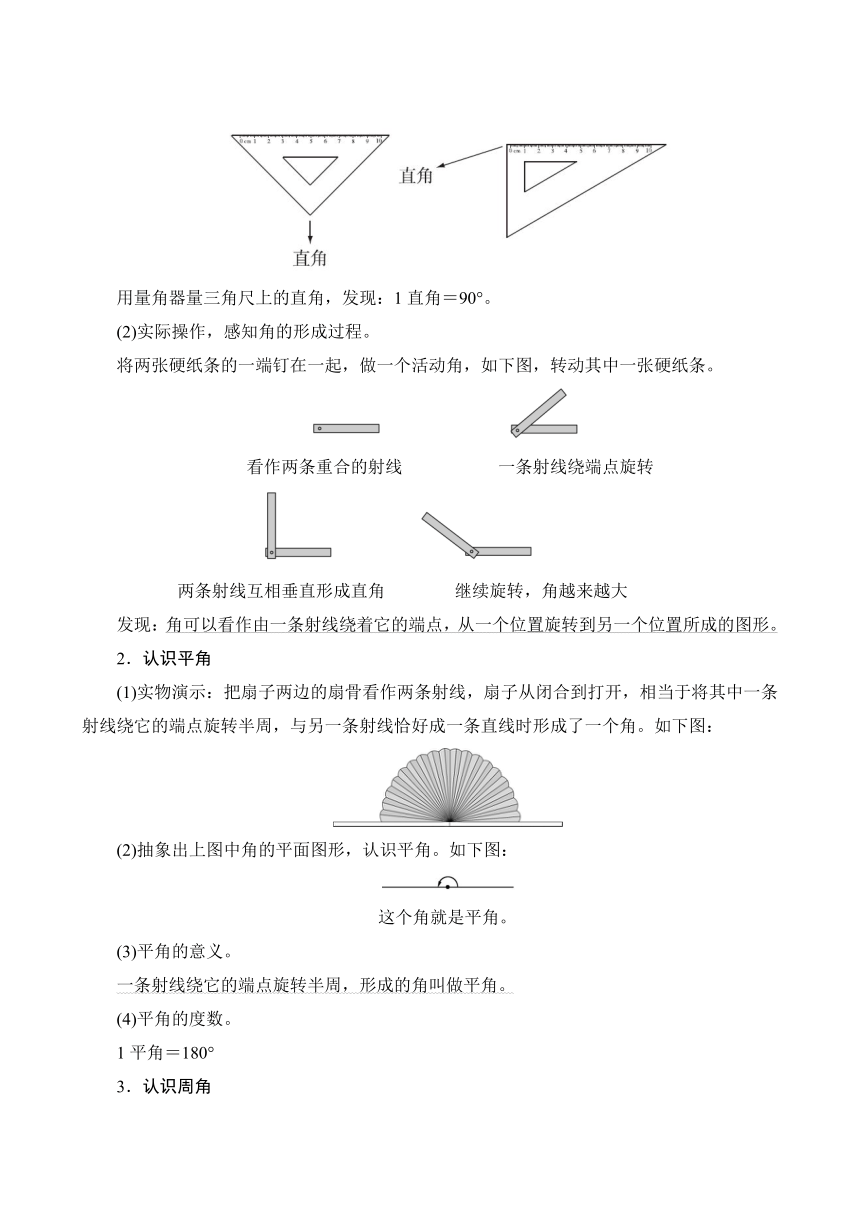
三角尺上有一个角是直角,如下图:
用量角器量三角尺上的直角,发现:1直角=90°。
(2)实际操作,感知角的形成过程。
将两张硬纸条的一端钉在一起,做一个活动角,如下图,转动其中一张硬纸条。
看作两条重合的射线 一条射线绕端点旋转
两条射线互相垂直形成直角 继续旋转,角越来越大
发现:角可以看作由一条射线绕着它的端点,从一个位置旋转到另一个位置所成的图形。
2.认识平角
(1)实物演示:把扇子两边的扇骨看作两条射线,扇子从闭合到打开,相当于将其中一条射线绕它的端点旋转半周,与另一条射线恰好成一条直线时形成了一个角。如下图:
(2)抽象出上图中角的平面图形,认识平角。如下图:
这个角就是平角。
(3)平角的意义。
一条射线绕它的端点旋转半周,形成的角叫做平角。
(4)平角的度数。
1平角=180°
3.认识周角
(1)实物演示:把扇子两边的扇骨看作两条射线,一条射线绕它的端点旋转一周,与另一条射线重合时形成了一个角。如下图:
(2)抽象出上图中角的平面图形,认识周角。如下图:
这个角就是周角。
(3)周角的意义。
易错提示
周角看起来是一条射线,其实是角的两条边重合在一起了。
一条射线绕它的端点旋转一周,形成的角叫做周角。
(4)周角的度数。
1周角=360°
4.平角和周角的画法
5.生活中的平角和周角
生活中的平角和周角有很多,如钟面上6时整,时针和分针成平角;12时整,时针和分针成周角。转动门的旋转、风车的旋转等都能形成平角和周角。
归纳总结
1.1直角=90° 1平角=180° 1周角=360°
2.平角的意义:一条射线绕它的端点旋转半周,形成的角叫做平角。
3.周角的意义:一条射线绕它的端点旋转一周,形成的角叫做周角。
拓展提高
周角并不是最大的角,当一条射线绕它的端点旋转几周时,所形成的角的度数就是几个360°。如跳水运动员做720°的转体动作时,就要在空中连续翻转两周。
知识点二 各类角之间的关系
问题导入 锐角、直角、钝角、平角和周角之间有什么关系?(教材42页例2)
过程讲解
1.列表比较
名称 锐角 直角 钝角 平角 周角
图形
度数 小于90° 等于90° 大于90°而 小于180° 等于180° 等于360°
定义 小于90°的角叫做锐角。 等于90°的角叫做直角。 大于90°而小于180°的角叫做钝角。 一条射线绕它的端点旋转半周,形成的角叫做平角。 一条射线绕它的端点旋转一周,形成的角叫做周角。
2.明确各类角之间的关系
锐角<直角<钝角<平角<周角
1周角=2平角=4直角
3.运用各类角之间的关系解决实际问题
如右图,量出∠1的度数,根据图中各个角之间的关系,就能算出其他三个角的度数。
量得∠1=130°,因为∠1和∠2形成一个平角,所以∠2=180°-∠1=180°-130°=50°。
以此类推:∠4=180°-∠1=180°-130°=50°,∠3=180°-∠2=180°-50°=130°。
归纳总结
各类角之间的关系:锐角<直角<钝角<平角<周角,1周角=2平角=4直角。
知识巧记
一周二平四直角,关系密切不得了。
钝角介于直平间,锐角不大比直小。
备易错易混
误区 判断:大于90°的角是钝角。(√)
错解分析 此题错在没有理解钝角的定义。大于90°的角,除钝角外,还有平角、周角等。
错解改正 ×
温馨提示
大于90°而小于180°的角是钝角。
备综合能力
方法运用 运用观察法解决求角的度数问题
典型例题 如图所示,∠1=∠2=∠3,且所有锐角的度数和为200°,∠1是多少度?(提示:所有锐角包括基本角和组合角)
思路分析 通过观察发现:(1)基本角有3个(∠1、∠2、∠3)
(2)2个基本角的组合角有2个 2×2=4(个)
(3)3个基本角的组合角有1个 1×3=3(个)
把所有锐角转化成基本角一共是3+4+3=10(个),即10个基本角的度数和为200°,由此可以求出1个基本角的度数,即∠1的度数。
正确解答 基本角的个数和:3+4+3=10(个) ∠1=200°÷10=20°
方法总结 解答此类问题的关键是将组合角的个数转化成基本角的个数。
规律运用 运用折起来的角与原角相等的规律解决求角的度数问题
典型例题 下面是一张长方形纸折起来以后的图形,其中∠1=60°,你知道∠2是多少度吗?
思路分析 求角的度数时,要注意各个角之间的关系。如上图,若把长方形纸折起来的部分展开,则可以发现2个∠2加1个∠1的度数和正好等于180°,已知∠1=60°,由此可以求出∠2的度数。
正确解答 ∠2=(180°-60°)÷2=60°
规律总结 解答此类问题的关键是明确折起来的角与原角相等。
备教学资源
七巧板的相关知识
七巧板也称“七巧图”“智慧板”,是民间流传的智力玩具。它是由宋代的宴几演变而来的,原为文人的一种室内游戏,后在民间演变为拼图板玩具。
七巧板是由五块三角形、一块正方形和一块平行四边形组成的。人们可以用七巧板随意地拼出自己设计的图案,但想用七巧板拼出特定的图案,就会遇到真正的挑战,这正是七巧板的乐趣所在。
备教材内容
1.本节课教学内容是角的分类,角的分类是第二学段“图形与几何”领域中的重要内容。
2.通过测量,让学生知道直角等于90°,从而使学生进一步认识直角,即从直观认识过渡到利用度数来定义。类似,对锐角、钝角的认识也需要上升到数学层面的抽象,即用度数范围来定义这两种角。对平角和周角的编排,教材是从动态的角度引出的,这更有利于学生对“角”的相关知识作系统认识。关于角的分类的编排,其重点在于结合分的过程对这几种角的特征作进一步的确认,特别是对锐角和钝角的再认识。此外,还要求学生去探索周角、平角和直角之间在度数方面的倍数关系。
3.教材先设计测量活动,让学生知道直角等于90°,从直观认知过渡到利用度数来定义直角,再通过两把折扇的实物图,让学生直观地理解平角、周角的概念,并且区别它们与直线、射线的关系,最后结合分类的过程进一步学习锐角、直角、钝角、平角、周角这几种角的特征,明确周角、平角和直角之间在度数方面的倍数关系。
4.角的分类是在学生已经初步认识直线、线段、射线、角以及会用量角器量角的基础上进行教学的。学习本节课的知识,可以学会根据各种角的度数及相互关系计算出指定角的度数,为后面的平面几何的学习作铺垫。
备教法学法
学生以前对锐角、钝角和直角已有直观层面的认识,所以在教学过程中,以研究直角作为教学的突破口,先让学生找出三角尺上的直角,用量角器测量,确认直角是90°,再动态演示直角的形成过程,然后呈现一些比90°大和比90°小的角,体会钝角和锐角的形成过程。当学生对钝角、直角、锐角有了抽象认识之后,再通过呈现扇子的形状抽象出平角和周角的形成过程,明确两者的概念。教学中,充分借助多媒体教学手段动态演示这五种角的形成过程,帮助学生理解不同角之间的关系。在学习过程中,学生通过量直角,画平角、周角,深刻体会它们的特征。以直角为突破口。学生以前对锐角、钝角和直角已有直观层面的认识,所以,以研究直角作为教学的突破口比较合理。教学中,可设计三个层次的活动:①测量三角尺上各个角的度数,确认直角为90°;②动态演示直角的形成过程,即一条射线绕着端点旋转90°后形成的图形;③呈现一些比90°大和比90°小的角,体会一定度数的钝角和锐角的形成过程。然后引出对180°的角(平角)和360°的角(周角)的认识。这样,可将5类角的关系建立在一个动态过程中来认识,有利于学生理解不同角之间的关系。加强操作,积累活动经验。活动可设计成两类:①度量和画一些特定度数的角,如量直角,画平角、周角,确认它
们的特点;②操作活动角去体会、想象、表征角的大小关系。特别在教学例2时,让学生摆
出不同的角,体会不同角的度数差异,并关注两个难点的处理:一是体会周角与0°角的区别;二是锐角和钝角的度数范围理解。
备已学知识
1.初步认识了钝角、直角、锐角,知道三者之间的关系:锐角<直角<钝角。
2.会用三角尺或直观观察判断出某一个角是锐角、直角还是钝角。
3.掌握了角的测量方法:把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合,角的另一边所对的量角器上的刻度就是这个角的度数。
备教学目标
1. 知道1 直角=90°、1 平角=180°、1 周角=360°,以及钝角与锐角的度数范围,了解这几种角的大小关系。
2. 经历动态认识各种角的形成过程,结合角的度数建构起各种角的概念表象,完成从直观到
抽象的认知过程。
3. 在学习过程中,培养探究意识,积累丰富的数学活动经验。
备教学重难点
重点:认识平角、周角,掌握锐角、直角、钝角、平角、周角之间的关系。引导学生能按一种合理的标准对角进行分类。
难点:周角是教学中的一个难点,因为周角比较特殊,角的两条边重合,教学时,我拿出活动角使学生看清把活动角旋转了一圈,然后,小结出周角的定义,让学生观察周角的画法,指指周角的顶点和两条边,从而明确周角的两条边重合在一起。
备知识讲解
知识点一 认识平角和周角
问题导入 我们已经认识了锐角、直角和钝角,你知道直角是多少度吗?你还认识其他的角吗?它们又有哪些特征呢?(教材42页)
过程讲解
1.明确直角的度数和角的形成过程
(1)明确直角的度数。
三角尺上有一个角是直角,如下图:
用量角器量三角尺上的直角,发现:1直角=90°。
(2)实际操作,感知角的形成过程。
将两张硬纸条的一端钉在一起,做一个活动角,如下图,转动其中一张硬纸条。
看作两条重合的射线 一条射线绕端点旋转
两条射线互相垂直形成直角 继续旋转,角越来越大
发现:角可以看作由一条射线绕着它的端点,从一个位置旋转到另一个位置所成的图形。
2.认识平角
(1)实物演示:把扇子两边的扇骨看作两条射线,扇子从闭合到打开,相当于将其中一条射线绕它的端点旋转半周,与另一条射线恰好成一条直线时形成了一个角。如下图:
(2)抽象出上图中角的平面图形,认识平角。如下图:
这个角就是平角。
(3)平角的意义。
一条射线绕它的端点旋转半周,形成的角叫做平角。
(4)平角的度数。
1平角=180°
3.认识周角
(1)实物演示:把扇子两边的扇骨看作两条射线,一条射线绕它的端点旋转一周,与另一条射线重合时形成了一个角。如下图:
(2)抽象出上图中角的平面图形,认识周角。如下图:
这个角就是周角。
(3)周角的意义。
易错提示
周角看起来是一条射线,其实是角的两条边重合在一起了。
一条射线绕它的端点旋转一周,形成的角叫做周角。
(4)周角的度数。
1周角=360°
4.平角和周角的画法
5.生活中的平角和周角
生活中的平角和周角有很多,如钟面上6时整,时针和分针成平角;12时整,时针和分针成周角。转动门的旋转、风车的旋转等都能形成平角和周角。
归纳总结
1.1直角=90° 1平角=180° 1周角=360°
2.平角的意义:一条射线绕它的端点旋转半周,形成的角叫做平角。
3.周角的意义:一条射线绕它的端点旋转一周,形成的角叫做周角。
拓展提高
周角并不是最大的角,当一条射线绕它的端点旋转几周时,所形成的角的度数就是几个360°。如跳水运动员做720°的转体动作时,就要在空中连续翻转两周。
知识点二 各类角之间的关系
问题导入 锐角、直角、钝角、平角和周角之间有什么关系?(教材42页例2)
过程讲解
1.列表比较
名称 锐角 直角 钝角 平角 周角
图形
度数 小于90° 等于90° 大于90°而 小于180° 等于180° 等于360°
定义 小于90°的角叫做锐角。 等于90°的角叫做直角。 大于90°而小于180°的角叫做钝角。 一条射线绕它的端点旋转半周,形成的角叫做平角。 一条射线绕它的端点旋转一周,形成的角叫做周角。
2.明确各类角之间的关系
锐角<直角<钝角<平角<周角
1周角=2平角=4直角
3.运用各类角之间的关系解决实际问题
如右图,量出∠1的度数,根据图中各个角之间的关系,就能算出其他三个角的度数。
量得∠1=130°,因为∠1和∠2形成一个平角,所以∠2=180°-∠1=180°-130°=50°。
以此类推:∠4=180°-∠1=180°-130°=50°,∠3=180°-∠2=180°-50°=130°。
归纳总结
各类角之间的关系:锐角<直角<钝角<平角<周角,1周角=2平角=4直角。
知识巧记
一周二平四直角,关系密切不得了。
钝角介于直平间,锐角不大比直小。
备易错易混
误区 判断:大于90°的角是钝角。(√)
错解分析 此题错在没有理解钝角的定义。大于90°的角,除钝角外,还有平角、周角等。
错解改正 ×
温馨提示
大于90°而小于180°的角是钝角。
备综合能力
方法运用 运用观察法解决求角的度数问题
典型例题 如图所示,∠1=∠2=∠3,且所有锐角的度数和为200°,∠1是多少度?(提示:所有锐角包括基本角和组合角)
思路分析 通过观察发现:(1)基本角有3个(∠1、∠2、∠3)
(2)2个基本角的组合角有2个 2×2=4(个)
(3)3个基本角的组合角有1个 1×3=3(个)
把所有锐角转化成基本角一共是3+4+3=10(个),即10个基本角的度数和为200°,由此可以求出1个基本角的度数,即∠1的度数。
正确解答 基本角的个数和:3+4+3=10(个) ∠1=200°÷10=20°
方法总结 解答此类问题的关键是将组合角的个数转化成基本角的个数。
规律运用 运用折起来的角与原角相等的规律解决求角的度数问题
典型例题 下面是一张长方形纸折起来以后的图形,其中∠1=60°,你知道∠2是多少度吗?
思路分析 求角的度数时,要注意各个角之间的关系。如上图,若把长方形纸折起来的部分展开,则可以发现2个∠2加1个∠1的度数和正好等于180°,已知∠1=60°,由此可以求出∠2的度数。
正确解答 ∠2=(180°-60°)÷2=60°
规律总结 解答此类问题的关键是明确折起来的角与原角相等。
备教学资源
七巧板的相关知识
七巧板也称“七巧图”“智慧板”,是民间流传的智力玩具。它是由宋代的宴几演变而来的,原为文人的一种室内游戏,后在民间演变为拼图板玩具。
七巧板是由五块三角形、一块正方形和一块平行四边形组成的。人们可以用七巧板随意地拼出自己设计的图案,但想用七巧板拼出特定的图案,就会遇到真正的挑战,这正是七巧板的乐趣所在。
