第三单元3.3《角的度量》(教案)-四年级上册数学人教版
文档属性
| 名称 | 第三单元3.3《角的度量》(教案)-四年级上册数学人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-15 14:04:23 | ||
图片预览



文档简介
备教材内容
1.本节课教学的是教材40页的内容、41页例1及做一做、44页练习七的相关习题。
2.度量角是小学阶段重要的操作技能之一,教材从角的大小比较引入该内容。事物间的模糊比较,有时靠直观判断即可,而要求精确比较时,则需要测量出具体数据。要精确判断∠2比∠1大多少,就得进行准确测量。于是引出测量标准(也就是单位)和测量工具。教材在介绍量角器之前,不仅提供了“角”的度量单位,还呈现了这个单位(即1°角)的产生
过程,并且说明正是根据这一原理制作了量角的工具——量角器,并帮助学生理解量角器的构成要素,为学生掌握用量角器量角的方法提供帮助。
3.教材内容分两个层次安排:第一层次是观察量角器,了解角的度量单位;第二层次是探究用量角器度量角的度数的方法。教材在学生初步认识了角,明确了角的概念,知道角有大小之分的基础上安排学习本节课的知识,学生学好这节课不仅能为后续学习角的分类和画角打下基础,也为今后学习几何知识作铺垫。
备教法学法
角的度量是在学生初步认识了角和直角,并明确了角的概念的基础上进行教学的,为学生以后学习角的分类和画角打下基础。本节课教学主要通过创设生动形象的教学情境,用直观的方式让学生充分感知、操作,通过小组合作交流,使学生在“做数学”的过程中认识角、探究并掌握用量角器量角的方法,从而体现以学生发展为本,培养学生的空间观念。为了实现教学目标,突出重点,有效降低难点。采取以下教学方法:从学生已有的知识入手,用自主探索,同伴交流等方式来掌握测量角的方法。通过动手操作,亲身体验来激发学生的学习兴趣,这样容易达到在学生头脑中建立各种角的表象,从而加快学生对角的度量的操作技能的形成。用先估后量的方式,防范学生读数错误,从而化解教学难点。问题引人,体会“单位”产生的必要性。问题是启发学生思考与探索的开始。在比较两个角的大小时,提出需要知道“相差多少”(或“∠2比∠1大多少”)这一问题,目的在于引发学生对测量单位和工具产生的需要的体验。了解单位产生的过程,理解量角器的构成要件和工作原理一般来说,教学前大多数学生已知道量角需要“量角器”,但对量角器的构造原理却不甚了解。教学中,可分三个层次组织教学:是请学生观察量角器的构成,尝试说明量角器上的数字所表达的意思;二是组织学生看教材内容或用多媒体演示角的单位产生的过程,演示过程中,引导学生关注1°角到2°角,再到3°角等依次递增的过程,引导学生观察并体会角的动态形成过程,为后续教学中理解平角和周角的动态定义莫定基础;三是再次回到量角器上,进一步理解量角器上的数字所表达的含义,特别关注“0°刻度线”和“1°角”的位置,为使用量角器量角的度数打下扎实的基础。
备教学目标
1.认识角的计量单位和量角器,培养有关角度的量感。
2.进一步认识角的大小,掌握用量角器量角的方法,积累有关测量的基本经验。
3.积极参与量角活动,运用角的知识描述相应的生活现象,感受图形与现实生活的密切联系。
备教学重难点
重点:掌握用量角器量角的方法。
难点:能区分量角器的内外圈刻度,并能正确读出角的度数。
备已学知识
从一点引出两条射线所组成的图形叫做角。这个点叫做角的顶点,这两条射线叫做角的边。如下图:
备知识讲解
知识点一 认识角的计量单位和量角器
问题导入 下面两个角哪个大些?大多少?(教材40页)
过程讲解
1.观图、读题,理解题意
已知两个角,要求比较这两个角的大小。
2.比较两个角的大小
(1)比较方法:用三角尺上的角来量一量、比一比。
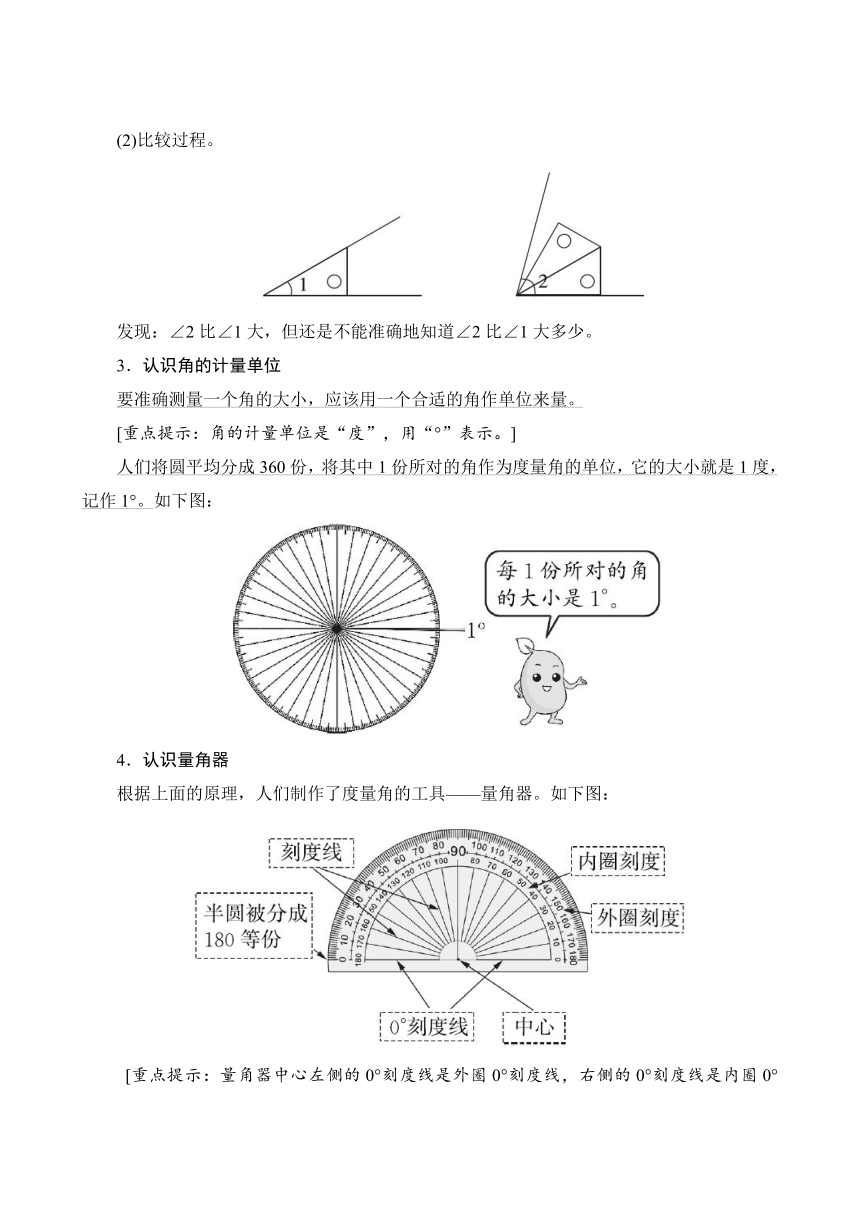
(2)比较过程。
发现:∠2比∠1大,但还是不能准确地知道∠2比∠1大多少。
3.认识角的计量单位
要准确测量一个角的大小,应该用一个合适的角作单位来量。
[重点提示:角的计量单位是“度”,用“°”表示。]
人们将圆平均分成360份,将其中1份所对的角作为度量角的单位,它的大小就是1度,记作1°。如下图:
4.认识量角器
根据上面的原理,人们制作了度量角的工具——量角器。如下图:
[重点提示:量角器中心左侧的0°刻度线是外圈0°刻度线,右侧的0°刻度线是内圈0°刻度线。]
发现:(1)半圆被分成180等份,每1份所对的角的大小是1°。
(2)中心两边各有一条0°刻度线,两条0°刻度线组成的角的大小是180°。
(3)量角器上有两圈刻度
5.在量角器上找出指定度数的角
例如:在量角器上找出50°和140°的角。
发现:同一度数的角既可以在内圈刻度中找到,又可以在外圈刻度中找到,只是角的开口方向不同。
归纳总结
知识点二 用量角器度量角的度数的方法
问题导入 怎样用量角器量出∠1的度数?(教材41页例1)
过程讲解
1.明确量角的步骤
(1)把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合。
(2)角的另一条边所对的量角器上的刻度,就是这个角的度数。
[方法提示:测量开口向右的角一般要看内圈刻度,测量开口向左的角一般要看外圈刻度。根据0°刻度线的位置确定好内、外圈刻度是准确读数的关键。]
2.量法展示
所以∠1=30°。
归纳总结
用量角器度量角的度数的基本方法和操作要领可以概括为“两重合,一对应”:
(1)两重合:①点点重合——量角器的中心与角的顶点重合;②线边重合——量角器的0°刻度线与角的一条边重合。
(2)一对应:角的另一条边所对的量角器上的刻度,就是这个角的度数。
知识巧记
角的度量并不难,度量方法要记全。
点点重合是关键,线边重合记心间。
内圈外圈不能混,读准度数才算完。
拓展提高
角的计量单位除了“度”以外,还有更小的计量单位“分”和“秒”,1分和1秒分别记作1′和1″,1°=60′,1′=60″。
备易错易混
误区 填空:这是一个(60)度的角。
错解分析 此题错在量角的度数时,内圈刻度与外圈刻度混用。当角的一条边与内圈的0°刻度线重合时,角的另一条边所对的刻度也应是内圈刻度。
错解改正 120
温馨提示
用量角器量角时,一定要分清内圈刻度与外圈刻度。
备综合能力
思维开放 运用列表法和归纳法解决数角的问题
典型例题 根据规律填一填。
思路分析 运用列表法探究每个图形中角的个数与射线条数之间的关系。如下表所示:
图形 射线条数 角的个数
2 1
3 2+1=3
4 3+2+1=6
5 4+3+2+1=10
…… n (n-1)+(n-2)+…+1
数角的个数时,找到角的个数与组成角的射线条数之间的规律,就能保证不重复、不遗漏。
正确解答 10
方法总结 从一个顶点引出n条射线,这n条射线组成的角的个数为[(n-1)+(n-2)+…+1]个。(n为大于1的自然数)
思维开放 运用观察法和推理法解决求时针和分针之间夹角的度数问题
典型例题 不用量角器,算出下面各钟面上时针和分针之间夹角的度数。
6时整,时针和分针在同一条直线上,所成的角的度数与量角器上的180°相同,所以时针和分针之间夹角的度数是180°。12和6之间有6个大格,每个大格的度数就是180°÷6=30°。所以当钟面上的时间是整时时,时针和分针所夹的角中有几个大格,所夹的角的度数就是几个30°。
思路分析 观察钟面,4个钟面上的时间都是整时,如果时针和分针所夹的角中1个大格的度数确定,那么所夹的角的度数就能确定。结合钟面和量角器的知识分析如下:
时间 时针和分针所夹角中的大格数/个 度数
4时 4 4×30°=120°
9时 3 3×30°=90°
7时 5 5×30°=150°
2时 2 2×30°=60°
正确解答 4个钟面上时针和分针之间夹角的度数分别是120°、90°、150°、60°。
方法提示 钟面上分针(或时针)转动1个大格就是30°,转动1个小格就是6°。
备教学资源
量角器的由来
半圆形的量角器是用来度量角的度数的。说到角度单位的发明,可要归功于中亚两河流域的古巴比伦人,据说当时的认知是一年有360天,因此,古巴比伦人发明出60进位的记数法则,并套用在角度的单位换算上,而一圈=360°、1°=60′(分)、1′=60″(秒)的习惯仍沿用至今,所以量角器可以说是“几何四宝”中名副其实的“舶来品”。
1.本节课教学的是教材40页的内容、41页例1及做一做、44页练习七的相关习题。
2.度量角是小学阶段重要的操作技能之一,教材从角的大小比较引入该内容。事物间的模糊比较,有时靠直观判断即可,而要求精确比较时,则需要测量出具体数据。要精确判断∠2比∠1大多少,就得进行准确测量。于是引出测量标准(也就是单位)和测量工具。教材在介绍量角器之前,不仅提供了“角”的度量单位,还呈现了这个单位(即1°角)的产生
过程,并且说明正是根据这一原理制作了量角的工具——量角器,并帮助学生理解量角器的构成要素,为学生掌握用量角器量角的方法提供帮助。
3.教材内容分两个层次安排:第一层次是观察量角器,了解角的度量单位;第二层次是探究用量角器度量角的度数的方法。教材在学生初步认识了角,明确了角的概念,知道角有大小之分的基础上安排学习本节课的知识,学生学好这节课不仅能为后续学习角的分类和画角打下基础,也为今后学习几何知识作铺垫。
备教法学法
角的度量是在学生初步认识了角和直角,并明确了角的概念的基础上进行教学的,为学生以后学习角的分类和画角打下基础。本节课教学主要通过创设生动形象的教学情境,用直观的方式让学生充分感知、操作,通过小组合作交流,使学生在“做数学”的过程中认识角、探究并掌握用量角器量角的方法,从而体现以学生发展为本,培养学生的空间观念。为了实现教学目标,突出重点,有效降低难点。采取以下教学方法:从学生已有的知识入手,用自主探索,同伴交流等方式来掌握测量角的方法。通过动手操作,亲身体验来激发学生的学习兴趣,这样容易达到在学生头脑中建立各种角的表象,从而加快学生对角的度量的操作技能的形成。用先估后量的方式,防范学生读数错误,从而化解教学难点。问题引人,体会“单位”产生的必要性。问题是启发学生思考与探索的开始。在比较两个角的大小时,提出需要知道“相差多少”(或“∠2比∠1大多少”)这一问题,目的在于引发学生对测量单位和工具产生的需要的体验。了解单位产生的过程,理解量角器的构成要件和工作原理一般来说,教学前大多数学生已知道量角需要“量角器”,但对量角器的构造原理却不甚了解。教学中,可分三个层次组织教学:是请学生观察量角器的构成,尝试说明量角器上的数字所表达的意思;二是组织学生看教材内容或用多媒体演示角的单位产生的过程,演示过程中,引导学生关注1°角到2°角,再到3°角等依次递增的过程,引导学生观察并体会角的动态形成过程,为后续教学中理解平角和周角的动态定义莫定基础;三是再次回到量角器上,进一步理解量角器上的数字所表达的含义,特别关注“0°刻度线”和“1°角”的位置,为使用量角器量角的度数打下扎实的基础。
备教学目标
1.认识角的计量单位和量角器,培养有关角度的量感。
2.进一步认识角的大小,掌握用量角器量角的方法,积累有关测量的基本经验。
3.积极参与量角活动,运用角的知识描述相应的生活现象,感受图形与现实生活的密切联系。
备教学重难点
重点:掌握用量角器量角的方法。
难点:能区分量角器的内外圈刻度,并能正确读出角的度数。
备已学知识
从一点引出两条射线所组成的图形叫做角。这个点叫做角的顶点,这两条射线叫做角的边。如下图:
备知识讲解
知识点一 认识角的计量单位和量角器
问题导入 下面两个角哪个大些?大多少?(教材40页)
过程讲解
1.观图、读题,理解题意
已知两个角,要求比较这两个角的大小。
2.比较两个角的大小
(1)比较方法:用三角尺上的角来量一量、比一比。
(2)比较过程。
发现:∠2比∠1大,但还是不能准确地知道∠2比∠1大多少。
3.认识角的计量单位
要准确测量一个角的大小,应该用一个合适的角作单位来量。
[重点提示:角的计量单位是“度”,用“°”表示。]
人们将圆平均分成360份,将其中1份所对的角作为度量角的单位,它的大小就是1度,记作1°。如下图:
4.认识量角器
根据上面的原理,人们制作了度量角的工具——量角器。如下图:
[重点提示:量角器中心左侧的0°刻度线是外圈0°刻度线,右侧的0°刻度线是内圈0°刻度线。]
发现:(1)半圆被分成180等份,每1份所对的角的大小是1°。
(2)中心两边各有一条0°刻度线,两条0°刻度线组成的角的大小是180°。
(3)量角器上有两圈刻度
5.在量角器上找出指定度数的角
例如:在量角器上找出50°和140°的角。
发现:同一度数的角既可以在内圈刻度中找到,又可以在外圈刻度中找到,只是角的开口方向不同。
归纳总结
知识点二 用量角器度量角的度数的方法
问题导入 怎样用量角器量出∠1的度数?(教材41页例1)
过程讲解
1.明确量角的步骤
(1)把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合。
(2)角的另一条边所对的量角器上的刻度,就是这个角的度数。
[方法提示:测量开口向右的角一般要看内圈刻度,测量开口向左的角一般要看外圈刻度。根据0°刻度线的位置确定好内、外圈刻度是准确读数的关键。]
2.量法展示
所以∠1=30°。
归纳总结
用量角器度量角的度数的基本方法和操作要领可以概括为“两重合,一对应”:
(1)两重合:①点点重合——量角器的中心与角的顶点重合;②线边重合——量角器的0°刻度线与角的一条边重合。
(2)一对应:角的另一条边所对的量角器上的刻度,就是这个角的度数。
知识巧记
角的度量并不难,度量方法要记全。
点点重合是关键,线边重合记心间。
内圈外圈不能混,读准度数才算完。
拓展提高
角的计量单位除了“度”以外,还有更小的计量单位“分”和“秒”,1分和1秒分别记作1′和1″,1°=60′,1′=60″。
备易错易混
误区 填空:这是一个(60)度的角。
错解分析 此题错在量角的度数时,内圈刻度与外圈刻度混用。当角的一条边与内圈的0°刻度线重合时,角的另一条边所对的刻度也应是内圈刻度。
错解改正 120
温馨提示
用量角器量角时,一定要分清内圈刻度与外圈刻度。
备综合能力
思维开放 运用列表法和归纳法解决数角的问题
典型例题 根据规律填一填。
思路分析 运用列表法探究每个图形中角的个数与射线条数之间的关系。如下表所示:
图形 射线条数 角的个数
2 1
3 2+1=3
4 3+2+1=6
5 4+3+2+1=10
…… n (n-1)+(n-2)+…+1
数角的个数时,找到角的个数与组成角的射线条数之间的规律,就能保证不重复、不遗漏。
正确解答 10
方法总结 从一个顶点引出n条射线,这n条射线组成的角的个数为[(n-1)+(n-2)+…+1]个。(n为大于1的自然数)
思维开放 运用观察法和推理法解决求时针和分针之间夹角的度数问题
典型例题 不用量角器,算出下面各钟面上时针和分针之间夹角的度数。
6时整,时针和分针在同一条直线上,所成的角的度数与量角器上的180°相同,所以时针和分针之间夹角的度数是180°。12和6之间有6个大格,每个大格的度数就是180°÷6=30°。所以当钟面上的时间是整时时,时针和分针所夹的角中有几个大格,所夹的角的度数就是几个30°。
思路分析 观察钟面,4个钟面上的时间都是整时,如果时针和分针所夹的角中1个大格的度数确定,那么所夹的角的度数就能确定。结合钟面和量角器的知识分析如下:
时间 时针和分针所夹角中的大格数/个 度数
4时 4 4×30°=120°
9时 3 3×30°=90°
7时 5 5×30°=150°
2时 2 2×30°=60°
正确解答 4个钟面上时针和分针之间夹角的度数分别是120°、90°、150°、60°。
方法提示 钟面上分针(或时针)转动1个大格就是30°,转动1个小格就是6°。
备教学资源
量角器的由来
半圆形的量角器是用来度量角的度数的。说到角度单位的发明,可要归功于中亚两河流域的古巴比伦人,据说当时的认知是一年有360天,因此,古巴比伦人发明出60进位的记数法则,并套用在角度的单位换算上,而一圈=360°、1°=60′(分)、1′=60″(秒)的习惯仍沿用至今,所以量角器可以说是“几何四宝”中名副其实的“舶来品”。
