第3节 水的浮力 重难点培优专题(含解析)
文档属性
| 名称 | 第3节 水的浮力 重难点培优专题(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2023-09-16 00:00:00 | ||
图片预览



文档简介
八上科学第一章第3节 水的浮力-重难点培优专题
考点一、液面高度变化的问题
液面变化问题主要可以总结为关于V排变化的分析。相对简单的试题只要把握好这一点即可。
将物体浸入(移出)柱形容器的液体中(如图1),若物体排开液体的体积为V排,容器的横截面积为S底,则物体浸入(移出)前后液面高度的变化量为=
浸入柱形容器中的柱形物体高出液面(如图2),当向容器中注入液体V加后,液面高度=
图1 图2 图3 图4
关于“冰化水”与“船载”问题
一块冰浮于水面,如图3那么当冰熔化前后,其水面将 (选填“升高”、“降低” 或“不变”)
证明:冰熔化前:由于漂浮,F浮=G物。则V排 = m冰g/ρ水g = m冰/ρ水。
冰熔化:由于m水= m冰,由ρ=m/V得 V化水=m水/ρ水=m冰/ρ水。
因 V排水= V化水,即冰熔化成水后,刚好填满原来被冰排开的水的体积,因此,水面保持不变。
① 若上题中的冰包含有气泡,则冰熔化后液面将如何变
② 若上题中的冰包有一小木块(ρ物<ρ水),则冰熔化后液面又将如何
③ 若上题中的冰包含有一小石块(ρ物>ρ水)则冰熔化后又如何
(2)如图4,铁块A叠放在木块B上,然后放在水缸中当将铁块从木块上拿下,并放在水缸底部时,水面高度将 。
二、如何用浮力知识来测固体或液体的密度
(1)测固体的密度
[例一] 请利用弹簧测力计、水、烧杯测出一块小石头(ρ物>ρ水)的密度。
① 实验原理 F浮=G-F拉 (称重法)
② 步骤:a 用弹簧测力计先测出小石块在空气中的重力记为G石,进而得出m石;
b 用弹簧测力计悬吊着小石块,使之浸没在水杯中。并记下此时弹簧测力计的示数为F拉;
c 由F浮+F拉=G可求得小石块浸没在水中受到的浮力为F浮=G石-F拉,由F浮=ρ液gV排得,算出V排;
d 由F浮=ρ液gV排和G=mg=ρ物gV物及V物=V排得ρ石= ρ水。
[例二] 利用量筒、水、细针测出不沉于水的蜡块密度(ρ物<ρ水)。
① 实验原理 F浮=G(漂浮法)
② 步骤:a 先往量筒中倒入适量的水,记下水的体积为V0;
b 然后往量筒中放入小蜡块,待小蜡块静止后,记下水面现在所对应的刻度为V1,即蜡块漂浮时V排=V1-V0;
c 用细针将蜡块全部按入水中,记下现在水面刻度为V2,此时蜡块的体积为V蜡=V2-V0;
d 利用漂浮条件F浮=G,即ρ水gV排=ρ蜡gV蜡得出ρ蜡=ρ水。
(2)测液体的密度
[方法一] 原理:F浮=G-F拉和F浮=ρ液gV排。(称重法)
器材:弹簧测力计、烧杯、适量的水、适量的待测液体和一个密度大于水和液体的物体。
过程:用上述器材分别测出物体在水中和待测液体中的浮力,则有
即:ρ液=。
[方法二]原理:F浮=G物(漂浮法)
器材:量筒、水和待测液体、一个密度比水和待测液体小的物体。
过程:用上述器材分别测出物体在水中和待测液体中的V排即可,即:由G物=F浮水和G物=F浮液可知ρ水gV排水=ρ液gV排液,也即ρ液=。
考点一、液面高度变化的问题
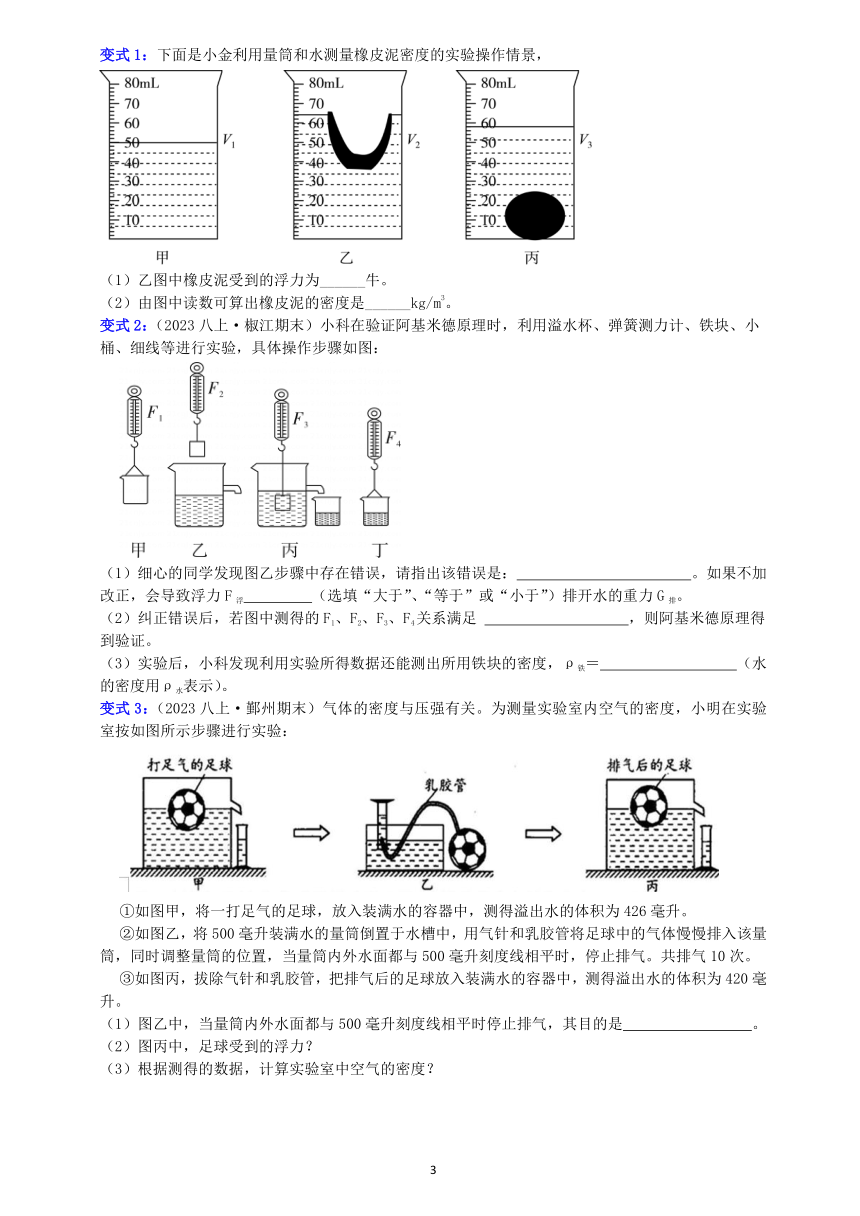
典例1:(2022八上·镇海期末)如图所示,一块冰放在盛有的水的容器中,已知冰块与容器底部相接触并相互间有压力,则当冰完全融化成水后,容器中水面的位置将 。
变式1:(2023八上·杭州期末)小金发现一冰块内有小石块,测得总质量是200g,放在水槽中,恰好悬浮在水中,则冰块与小石块的总体积是 cm3。当冰熔化后小石块沉入了水槽底,此时水槽中的水面 (选填“上升”、“下降”或“不变”)。(ρ水=1×103kg/m3,ρ冰=0.9×103kg/m3)
变式2:(2022八上·余姚期末)如图所示,在一个足够深的水槽中漂浮着一个木杯,此时杯口到水面的垂直距离为h,水槽底部到水面的垂直距离为H,若从水槽中取少量水倒入木杯中,则h (填“变大”,“变小”或“不变”,下同),H 。
(2) (3)
变式3:(2022·浙江台州·八年级期末)小金把家里景观水池底部的鹅卵石取出清洗,他先将一个重为15N的空桶漂浮在水面上,然后将池底的鹅卵石捞出放置在桶内,桶仍漂浮在水面(不考虑捞出过程中带出的水,ρ水=1.0×103kg/m3)
(1)某块鹅卵石在水池底部时,它受到的浮力 它的重力(选填“大于”、“小于”或“等于”)。
(2)全部鹅卵石捞出放置在桶内时,水池内水面高度与鹅卵石未捞出时相比会_______(选填“上升”、“下降”或“不变”)。若此时桶排开水的体积为5.0×10-3m3,求桶内鹅卵石的总质量。
考点二、利用浮力测物体密度
典例1:(2022八上·宁海期中)小明用装有适量水的薄壁小试管、螺母和细线制成一个测量小石块密度的装置。将此装置放入水中静止时,试管署出水面的高度h1为5cm,如图甲所示:在试管中轻轻放入小石块,装夏在水中静止时,试管露出水面的高度h2为2cm,如图乙所示。已知小石块放入试管前后.试管中的液面差h3为2cm。则
(1)小试管所受浮力的方向为
(2)石块的密度为 kg/m3
变式1:下面是小金利用量筒和水测量橡皮泥密度的实验操作情景,
(1)乙图中橡皮泥受到的浮力为______牛。
(2)由图中读数可算出橡皮泥的密度是______kg/m3。
变式2:(2023八上·椒江期末)小科在验证阿基米德原理时,利用溢水杯、弹簧测力计、铁块、小桶、细线等进行实验,具体操作步骤如图:
(1)细心的同学发现图乙步骤中存在错误,请指出该错误是: 。如果不加改正,会导致浮力F浮 (选填“大于”、“等于”或“小于”)排开水的重力G排。
(2)纠正错误后,若图中测得的F1、F2、F3、F4关系满足 ,则阿基米德原理得到验证。
(3)实验后,小科发现利用实验所得数据还能测出所用铁块的密度,ρ铁= (水的密度用ρ水表示)。
变式3:(2023八上·鄞州期末)气体的密度与压强有关。为测量实验室内空气的密度,小明在实验室按如图所示步骤进行实验:
①如图甲,将一打足气的足球,放入装满水的容器中,测得溢出水的体积为426毫升。
②如图乙,将500毫升装满水的量筒倒置于水槽中,用气针和乳胶管将足球中的气体慢慢排入该量筒,同时调整量筒的位置,当量筒内外水面都与500毫升刻度线相平时,停止排气。共排气10次。
③如图丙,拔除气针和乳胶管,把排气后的足球放入装满水的容器中,测得溢出水的体积为420毫升。
(1)图乙中,当量筒内外水面都与500毫升刻度线相平时停止排气,其目的是 。
(2)图丙中,足球受到的浮力?
(3)根据测得的数据,计算实验室中空气的密度?
4.[2021·丽水] 归纳与演绎是科学学习中非常重要的科学方法,下表是兴趣小组归纳“根据ρ=,运用浮力知识间接测量固体密度”的方法,请完成表格。
方法 实验器材 操作过程 思维过程 数据处理 适用范围
一 弹簧测力计、烧杯、水 m=,V物=V排=,ρ物=== ρ物= kg/m3 ρ物>ρ液
二 量筒、细铁丝、水 ……ρ物= ( 用V1、V2、V3、ρ水表示) …… ρ物<ρ液
5.张超同学利用量筒和水测量橡皮泥的密度,请根据图完成下列填空。
(1)在量筒中装适量的水,读出水面对应的刻度值V1= 。
(2)把橡皮泥捏成碗状,小心放入量筒使之漂浮在水面上,读出此时水面对应的刻度值V2,根据漂浮原理可求出橡皮泥的质量m= 。(g取10 N/kg)
(3)再把橡皮泥团成球放入量筒使之沉入水底,读出此时水面对应的刻度值V3。
(4)利用密度计算公式可推导出橡皮泥密度的表达式为ρ= 。由图中读数可算出橡皮泥的密度是 kg/m3。
6.小晨设计了一个用排水法测某实心金属块的密度的实验。实验器材有小空桶、溢水杯、烧杯、量筒和水。实验步骤如下:
①让小空桶漂浮在盛满水的溢水杯中,如图 甲所示;
②将金属块浸没在水中,测得溢出水的体积为20 mL,如图乙所示;
③将烧杯中 20 mL水倒掉,从水中取出金属块,如图丙所示;
④将金属块放入小空桶,小空桶仍漂浮在水面上,测得此时溢出水的体积为 44 mL,如图丁所示。
请回答下列问题:
(1)被测金属块的密度是 g/cm3。(g取10 N/kg)
(2)在实验步骤③和④中,将沾有水的金属块放入小空桶,测出的金属块的密度将 (填“偏大”“不变”或“偏小”)。
考点三、浮力与曲线变化
典例1:(2022八上·余姚期中)将一个底面积为 0.01 m2的长方体木块用细线拴在一个空容器的底部,然后向容器中缓慢加水直到木块上表面与液面相平,如图甲所示。在整个过程中,木块底部受到水的压强随容器中水的深度的变化如图乙所示,则木块所受到的最大浮力为 N,木块重力为 N,细线对木块的最大拉力为 N。
变式1:(2022八上·鄞州期中)如图甲所示,一个棱长为10cm、重为9N的正方体物块M,水平放置在一个方形容器中,M与容器底部不密合。以恒定水流向容器内注水,容器中水M的深度h随时间t的变化关系如图乙所示,当t=100s时,物块M在水中处于 (选填“沉底”、“悬浮”或“漂浮”)状态,图乙中a的值为 cm。
变式2:(2020八上·奉化期末)如图甲所示,在容器底部固定一轻质弹簧,弹簧受到的拉力跟弹簧的伸长量关系如图乙所示,弹簧上端连有一边长为0.1m的正方体物块A,当容器中水的深度为20cm时,物块A有2/5的体积露出水面,此时弹簧恰好处于自然伸长状态。求:
(1)物块A的密度。
(2)往容器缓慢加水(水未溢出)至物块A恰好浸没时,弹簧的伸长量为多少 再继续加水,木块受到浮力怎么变化
变式3:(2022八上·平阳月考)如图甲所示,一个边长是10cm的立方体木块,下面用一段细线与木块相连,细线另一端固定在容器底(容器高比细线与木块边长之和大得多)。现向容器中慢慢加水,直到细线拉直,如图乙所示。若细线的拉力用F表示,倒入容器中水的深度用h表示(g= 10 N/kg)。
(1)图丙中的A点对应木块在水中的位置是处于 状态。
(2)该木块浸没在水中所受的浮力为多少牛顿?
(3)该木块的密度为多少?
(4)请在丁图中作此过程中木块所受浮力F浮随水的深度h变化的大致图象。
考点四、浮力的受力分析计算
典例1:(2023八上·海曙期末)如图,体积相同的两物体A、B用不可伸长的细线系住,放入水中后,A有四分之一体积露出水面,细线被拉直。已知A重4N,B受到的浮力为8N,A、B密度之比为2:5。那么下列说法正确的是( )
A,B所受的重力之比为5:2
B.A、B所受的浮力之比为1:4
C.细线对A的拉力大小为1N
D.B对容器底部的压力为零
变式1:(2022八上·平阳月考)物体浮在甲液面时有1/5的体积露出液面,物体浮在乙液面时有1/3的体积露出液面,则甲、乙两液体的密度之比是( )
A.5 :12 B.4 :15 C.5 :6 D.12 :5
变式2:如图用细线将正方体A和物体B相连放入水中,两物体静止后恰好悬浮,此时A上表面到水面的高度差为0.12m。已知A的体积为1.0×10﹣3m3,所受重力为8N;B的体积为0.5×10﹣3m3,g取10N/kg,求:(1)A的密度;
(2)细线对B的拉力大小。
变式3:如图所示,在一个装满水的容器中,轻质弹簧的一端连着小球,另一端固定在容器底部。已知小球的体积是500cm3,小球静止时受到弹簧对它的作用力为4N。则:
(1)此时小球受到的浮力为多少?
(2)如果剪断弹簧后,请分析小球的运动情况,并计算再次静止后小球受到的浮力是多少?
课后巩固
1.如图,一杯果汁(密度大于水),加冰后液面正好同杯口相平。则在冰块熔化过程中( )
A.液面不变,液体不溢出 B.液面不变,液体溢出 C.液面下降 D.无法确定
(1) (2) (3)
2.如图所示,容器内有水,有一试管下面挂一小铁块,浮在水面上。现将小铁块取下放入试管中,试管仍浮在水面,则( )
A.液面上升 B.试管底部受到液体的压强变大
C.液面下降 D.试管所受到的浮力不变
5.(2023八上·宁海期末)水平桌面上两个相同的烧杯中分别装有甲、乙两种不同液体,将两个用不同材料制成的正方体A、B(VA<VB),按如图两种方式放入两种液体中,待静止后B刚好浸没在甲液体中,两杯中液面恰好相平。下列说法正确的是( )
A.甲液体的密度大于乙液体的密度
B.甲液体对杯底的压强等于乙液体对杯底的压强
C.甲液体对B下表面的压强等于乙液体对A下表面的压强
D.装甲液体的烧杯对水平桌面的压力小于装乙液体的烧杯对水平桌面的压力
3.(2023八上·杭州期末)把一个木球轻轻放入盛满水的溢杯中(足够大),溢出100g水;若将此木球从水中取出,擦干后轻轻放入盛满酒精的溢杯中(足够大),则溢出酒精的质量是(ρ木=0.6×103kg/m3,ρ酒精=0.8×103kg/m3,ρ水=1×103kg/m3)( )
A.大于100g B.等于100g C.小于100g D.无法确定
4.(2022八上·杭州期中)将一个物块轻轻放入盛满水的烧杯中,静止后有81克水从烧杯中溢出;将其轻轻放入盛满酒精的烧杯中,静止后有72克酒精从烧杯中溢出。已知酒精密度:0.8×103kg/m3,则该物块在水中的状态及物块的密度分别为( )
A.悬浮 1.0×103kg/m3 B.漂浮 0.9×103kg/m3
C.漂浮 0.92×103kg/m3 D.下沉 1.2×103kg/m3
6.(2023八上·宁海期末)迪迪同学将质量为120g的物体放入盛满水的溢水杯中,当物体静止时,溢水杯中溢出了100cm3的水,物体受到的浮力为 N,则此时物体在水中 (选填“漂浮”、“悬浮”或“沉底”).
7.(2022八上·富阳期中)小科按照教材中"综合实践活动"的要求制作简易密度计。
(1)取一根粗细均匀的饮料吸管,在其下端塞入适量金属丝并用石蜡封口。塞入金属丝的目的是使吸管能漂浮在液体中。这根吸管竖直漂浮在不同液体中时,液体密度越大,它露出液面部分的长度 (选填“越长”、“越短”或“”不变”)
(2)小科根据图甲在吸管上标出1.0刻度线(单位g/cm , 下同),再利用上述关系式进行计算,标出了0.9、1.0、1.1的刻度线,如图乙A,B,C,D所示,则标示正确的图是
(3)将吸管放到水中的情境如丙图(a)所示,测得浸入的长度为H;放到另一液体中的情景如丙图(b)所示,浸入的长度为h。用ρ液、ρ水分别表示液体和水的密度,则h和ρ水、ρ液,H的关系式是h= 。
8.(2023八上·义乌期末)小明利用电子秤、长方体铁块、细线、圆柱形玻璃板、糖水,探究“影响浮力大小的因素”实验。
(1)如图甲,将搅拌均匀的糖水装入柱形杯中,置于电子秤上,示数为400.0g。用质量和体积均不计的细线系好铁块,缓慢浸入装有糖水的容器中,直到乙图所示的位置,发现该过程中电子秤示数逐渐增大。说明:铁块所受浮力大小与
有关;
(2)继续将铁块缓慢浸没到图丙所示位置,通过观察与比较,小明认为物体所受浮力大小与浸没后的深度
(选填“有关”或“无关”);
(3)将铁块沉入杯底,松开细线(细线已松弛),此时电子秤的示数如图丁所示,糖水密度为
kg/m3;(铁的密度是7.9克/厘米3)
(4)放置一段时间后,将铁块从糖水中慢慢提起。小明发现铁块离开杯底至上表面露出液面前,电子秤示数逐渐减小,造成这种现象的主要原因可能是
。
9.(2020八上·余杭月考)人们常用“冰山一角"来形容事物显露出来的仅仅是其很小的部分,更多的还隐藏在表面现象之下。事实上,冰山浮在海水中的确只露”一角"(如图所示)。若现有一座冰山,它露出海面的体积是2000m3 , (已知:海水的密度取ρ海水=1×103kg/m3 , 冰的密度ρ冰=0.9×103kg/m3)。则:
(1)假如此冰山完全熔化,则液面将________(填“不变”、“降低”或“上升");
(2)这座冰山的总体积为多少?
10.(2022八上·鹿城月考)小华发现用密度计测量液体密度需要大量液体,因此他用家里闲置的眼镜盒自制了密度计,该自制密度计高为16厘米,横截面积为20cm2,在盒子底部加入沙子使密度计能竖立水中,密度计自重200克。使用时烧杯中装有一定量的水。求:
(1)未放入待测液体之前,该密度计所受浮力多大
(2)往密度计中放入10毫升待测液,密度计浸入深度为10.6cm,则待测液的密度为多少
(3)为了提高自制密度计的精确度,请提出一条改进建议:
11.(2022八上·慈溪月考)如图甲所示,水平放置的方形容器里有一个重为9 N、边长为10 cm的立方体物块M,M与容器底部不密合。以6 mL/s的恒定水流向容器内注水,容器中水的深度h随时间t的变化关系如图乙所示。求:
(1)当t=100 s时,物块M在水中处于 (选填“沉底”“悬浮"或“漂浮”)状态。
(2)当t=100 s时,水对容器底部的压力大小是多少
(3)图乙中a的值是多少
12.(2022八上·长兴)边长为10cm的正方体物块放入水平桌面上的圆柱形容器底部(如图甲所示),逐渐向容器内倒入适量水(水未溢出),测量容器内水的深度h,分别计算出物块对应受到的浮力F浮,并绘制了如图乙(实线)所示的图象。把水换成液体A重复上述实验,绘制了如图乙(虚线)所示的图像。
(1)由图乙可知,正方体物块受到的重力为 N。
(2)正方体物块的密度为多少?
(3)液体A的密度为多少?
第3节 水的浮力3-重难点培优
考点一、液面高度变化的问题
液面变化问题主要可以总结为关于V排变化的分析。相对简单的试题只要把握好这一点即可。
将物体浸入(移出)柱形容器的液体中(如图1),若物体排开液体的体积为V排,容器的横截面积为S底,则物体浸入(移出)前后液面高度的变化量为=
浸入柱形容器中的柱形物体高出液面(如图2),当向容器中注入液体V加后,液面高度=
图1 图2 图3 图4
关于“冰化水”与“船载”问题
一块冰浮于水面,如图3那么当冰熔化前后,其水面将 (选填“升高”、“降低” 或“不变”)
证明:冰熔化前:由于漂浮,F浮=G物。则V排 = m冰g/ρ水g = m冰/ρ水。
冰熔化:由于m水= m冰,由ρ=m/V得 V化水=m水/ρ水=m冰/ρ水。
因 V排水= V化水,即冰熔化成水后,刚好填满原来被冰排开的水的体积,因此,水面保持不变。
① 若上题中的冰包含有气泡,则冰熔化后液面将如何变
② 若上题中的冰包有一小木块(ρ物<ρ水),则冰熔化后液面又将如何
③ 若上题中的冰包含有一小石块(ρ物>ρ水)则冰熔化后又如何
(2)如图4,铁块A叠放在木块B上,然后放在水缸中当将铁块从木块上拿下,并放在水缸底部时,水面高度将
知识点 不变 降低
二、如何用浮力知识来测固体或液体的密度
(1)测固体的密度
[例一] 请利用弹簧测力计、水、烧杯测出一块小石头(ρ物>ρ水)的密度。
① 实验原理 F浮=G-F拉 (称重法)
② 步骤:a 用弹簧测力计先测出小石块在空气中的重力记为G石,进而得出m石;
b 用弹簧测力计悬吊着小石块,使之浸没在水杯中。并记下此时弹簧测力计的示数为F拉;
c 由F浮+F拉=G可求得小石块浸没在水中受到的浮力为F浮=G石-F拉,由F浮=ρ液gV排得,算出V排;
d 由F浮=ρ液gV排和G=mg=ρ物gV物及V物=V排得ρ石= ρ水。
[例二] 利用量筒、水、细针测出不沉于水的蜡块密度(ρ物<ρ水)。
① 实验原理 F浮=G(漂浮法)
② 步骤:a 先往量筒中倒入适量的水,记下水的体积为V0;
b 然后往量筒中放入小蜡块,待小蜡块静止后,记下水面现在所对应的刻度为V1,即蜡块漂浮时V排=V1-V0;
c 用细针将蜡块全部按入水中,记下现在水面刻度为V2,此时蜡块的体积为V蜡=V2-V0;
d 利用漂浮条件F浮=G,即ρ水gV排=ρ蜡gV蜡得出ρ蜡=ρ水。
(2)测液体的密度
[方法一]
原理:F浮=G-F拉和F浮=ρ液gV排。(称重法)
器材:弹簧测力计、烧杯、适量的水、适量的待测液体和一个密度大于水和液体的物体。
过程:用上述器材分别测出物体在水中和待测液体中的浮力,则有
即:ρ液=。
[方法二]
原理:F浮=G物(漂浮法)
器材:量筒、水和待测液体、一个密度比水和待测液体小的物体。
过程:用上述器材分别测出物体在水中和待测液体中的V排即可,即:由G物=F浮水和G物=F浮液可知ρ水gV排水=ρ液gV排液,也即ρ液=。
考点一、液面高度变化的问题
典例1:(2022八上·镇海期末)如图所示,一块冰放在盛有的水的容器中,已知冰块与容器底部相接触并相互间有压力,则当冰完全融化成水后,容器中水面的位置将 。
【答案】上升
【解析】水面上升还是下降,取决于冰块排开水的体积与熔化成水后体积的大小关系,据此分析解答。
【解答】冰熔化前,它受到竖直向上的浮力和支持力,以及竖直向下的重力,
根据二力平衡的知识得到:F浮+F支=G冰,
所以F浮=ρ水V排g<G冰, ①
冰化水后质量不变,
根据G=mg可知,重力不变,即G冰=G水,
即:ρ冰V冰g=ρ水V水g ②
由①②可得:
ρ水V排g<ρ水V水g,
即:冰熔化为水的体积大于排开水的体积,
所以冰熔化后,水面将上升。
变式1:(2023八上·杭州期末)小金发现一冰块内有小石块,测得总质量是200g,放在水槽中,恰好悬浮在水中,则冰块与小石块的总体积是 cm3。当冰熔化后小石块沉入了水槽底,此时水槽中的水面 (选填“上升”、“下降”或“不变”)。(ρ水=1×103kg/m3,ρ冰=0.9×103kg/m3)
【答案】200;下降
【解析】(1)根据悬浮条件确定冰块的平均速度,再根据计算二者的总体积;
(2)将冰块熔化前二者排开水的总体积与熔化后水和石块的总体积进行比较即可。
【解答】(1)冰块和石块在水中悬浮,则它们的平均密度等于水的密度;
那么二者的总体积为:;
(2)冰块熔化前,二者在水中悬浮,则它们受到的浮力等于总重力;
冰块熔化后,此时冰块变成的水可以看似在水中悬浮,因此冰块受到的浮力不变;
而石块在水中下沉,那么它受到的浮力小于石块重力;
即冰块和石块受到的浮力小于它们的总重力;比较可知,它们受到的浮力减小了;
根据阿基米德原理F浮=ρ液gV排可知,它们排开水的总体积减小了,
那么水槽中的水面下降。
变式2:(2022八上·余姚期末)如图所示,在一个足够深的水槽中漂浮着一个木杯,此时杯口到水面的垂直距离为h,水槽底部到水面的垂直距离为H,若从水槽中取少量水倒入木杯中,则h (填“变大”,“变小”或“不变”,下同),H 。
【答案】变小;不变
【解析】(1)根据浮沉条件比较浮力的大小变化,再根据阿基米德原理F浮力=ρ液gV排分析水杯排开水的体积变化,根据V=Sh分析浸入深度的变化,从而确定露出水面高度的变化。
(2)水面高度的变化取决于水和杯子排开水的总体积的变化。
【解答】(1)水杯始终在水面漂浮,则它受到的浮力始终等于自身重力。从水槽中取少量的水倒入杯子中后,杯子的重力增大,则它受到的浮力增大。根据据阿基米德原理F浮力=ρ液gV排可知,杯子排开水的体积增大。根据V=Sh可知,杯子浸入水中的深度变大,而露出水面的高度h减小。
(2)原来杯子在水面漂浮,它受到的浮力等于重力,
则水和杯子排开水的总体积为:V总=V水+V排=V水+;
从水槽中取出少量水倒入杯子中后,杯子和水受到的浮力等于它们的总重力,
此时水和杯子排开水的总体积为:V总'=V水-V取出+=V水-V取出++;
而V取出=; 因此V总=V总';
即水和杯子排开水的总体积保持不变; 因此水面高度H保持不变。
变式3:(2022·浙江台州·八年级期末)小金把家里景观水池底部的鹅卵石取出清洗,他先将一个重为15N的空桶漂浮在水面上,然后将池底的鹅卵石捞出放置在桶内,桶仍漂浮在水面(不考虑捞出过程中带出的水,ρ水=1.0×103kg/m3)
(1)某块鹅卵石在水池底部时,它受到的浮力 它的重力(选填“大于”、“小于”或“等于”)。
(2)全部鹅卵石捞出放置在桶内时,水池内水面高度与鹅卵石未捞出时相比会_______(选填“上升”、“下降”或“不变”)。若此时桶排开水的体积为5.0×10-3m3,求桶内鹅卵石的总质量。
【答案】(1)小于
(2)上升;
F浮总=ρ液gV排=1×103Kg/m3×10N/kg×5.0×10-3m3=50N G石=F浮总-G桶=50N-15N=35N
【解析】(1)根据浮沉条件比较浮力和重力的大小
(2)水面上升还是下降,取决于鹅卵石排开水的体积大小,根据阿基米德原理F浮=ρ液gV排比较即可。
首先根据阿基米德原理F浮=ρ液gV排计算出桶和鹅卵石受到的总浮力,再根据G石=F浮总-G桶计算出鹅卵石的重力,最后根据计算出鹅卵石的质量。
【解答】(1)鹅卵石在池水里处于下沉状态,则它受到的浮力小于重力。
(2)鹅卵石在桶内处于漂浮状态,则此时它受到的浮力大于沉在池底时的浮力。根据阿基米德原理F浮=ρ液gV排可知,则此时它排开水的体积大于沉在池底时的体积,因此水池内水面高度与未捞出时相比会上升。
和鹅卵石受到的总浮力F浮总=ρ液gV排=1×103kg/m3×10N/kg×5.0×10-3m3=50N;
鹅卵石的重力:G石=F浮总-G桶=50N-15N=35N ;
鹅卵石的质量:。
考点二、利用浮力测物体密度
典例1:(2022八上·宁海期中)小明用装有适量水的薄壁小试管、螺母和细线制成一个测量小石块密度的装置。将此装置放入水中静止时,试管署出水面的高度h1为5cm,如图甲所示:在试管中轻轻放入小石块,装夏在水中静止时,试管露出水面的高度h2为2cm,如图乙所示。已知小石块放入试管前后.试管中的液面差h3为2cm。则
(1)小试管所受浮力的方向为
(2)石块的密度为 kg/m3
【答案】(1)竖直向上
(2)3×103
【解析】(1)浮力的方向为竖直向上;
(2)比较甲、乙两图可知,试管两次受到的浮力之差就是小石块的重力;进一步求出小石块的质量;
根据小石块放入试管前后,试管中的液面差h3为2cm可以求出小石块的体积;最后利用密度公式求出小石块的密度。
【解答】(1)小试管所受浮力的方向为竖直向上;
(2)比较甲、乙两图可知,两次受到的浮力之差就是小石块的重力,
即石块的重力G=ΔF浮=ρ水g(h1-h2)S容=ρ水g×(0.05m-0.02m)S容=ρ水gS容×0.03m,
小石块放入试管前后,试管中的液面差h3为2cm,
所以小石块的体积为V=(h1-h2-h3)S容=(0.05m-0.02m-0.02m)S容=0.01m×S容,
则小石块的密度。
变式1:下面是小金利用量筒和水测量橡皮泥密度的实验操作情景,
(1)乙图中橡皮泥受到的浮力为______牛。
(2)由图中读数可算出橡皮泥的密度是______kg/m3。
【答案】0.14 1.75×103
【解析】解:(1)[1]橡皮泥浸没之前水面对应的示数为V1=50mL=50cm3
橡皮泥漂浮在水面上水面对应的示数为V2=64mL=64cm3
乙图中橡皮泥排开液体的体积V'=V2-V1=64mL-50mL=14mL=14cm3=1.4×10-5m3
乙图中橡皮泥受到的浮力为F浮=ρ水gV排=1.0×103kg/m3×10N/kg×1.4×10-5m3=0.14N
(2)[2]橡皮泥团成球浸没在水中,量筒中水面对应的示数为V3=58mL=58cm3
橡皮泥漂浮在水面上,受到的重力等于排开水的重力,所以橡皮泥的质量等于排开水的质量,所以
m=m排水=(V2-V1)ρ水
橡皮泥的体积为V=V3-V1
所以橡皮泥的密度
变式2:(2023八上·椒江期末)小科在验证阿基米德原理时,利用溢水杯、弹簧测力计、铁块、小桶、细线等进行实验,具体操作步骤如图:
(1)细心的同学发现图乙步骤中存在错误,请指出该错误是: 。如果不加改正,会导致浮力F浮 (选填“大于”、“等于”或“小于”)排开水的重力G排。
(2)纠正错误后,若图中测得的F1、F2、F3、F4关系满足 ,则阿基米德原理得到验证。
(3)实验后,小科发现利用实验所得数据还能测出所用铁块的密度,ρ铁= (水的密度用ρ水表示)。
【答案】(1)溢水杯中没有装满水;大于
(2)F2﹣F3=F4﹣F1
(3) ρ水
【解析】(1)根据图乙可知,当溢水杯中装满水时,物体排开水的重力才会恰好等于它受到的浮力。如果没有装满水,那么放入物体后水面先上升到溢水杯口才会有水排出,而不是马上排出水,据此比较浮力和排开水的重力大小。
(2)根据阿基米德原理F浮=G排分析解答;
(3)根据称量法计算出铁块受到浮力,根据阿基米德原理计算出铁块的体积,根据密度公式计算铁块的密度。
【解答】(1)根据图片可知,图乙中存在的错误:溢水杯中没有装满水。如果不加改正,会导致浮力F浮大于排开水的重力G排。
(2)根据图片可知,图乙中物体的重力G=F2,丙图中物体浸没时测力计的示数为F3,
则物体受到的浮力:F浮=G-F拉=F2-F3;
空桶的重力G桶=F1,桶和排出水的总重力G总=F4;
则物体排开水的重力G排=G总-G桶=F4-F1;
根据阿基米德原理F浮=G排得到:F2-F3=F4-F1。
(3)综上所述,铁块的体积:;
则铁块的密度:。
变式3:(2023八上·鄞州期末)气体的密度与压强有关。为测量实验室内空气的密度,小明在实验室按如图所示步骤进行实验:
①如图甲,将一打足气的足球,放入装满水的容器中,测得溢出水的体积为426毫升。
②如图乙,将500毫升装满水的量筒倒置于水槽中,用气针和乳胶管将足球中的气体慢慢排入该量筒,同时调整量筒的位置,当量筒内外水面都与500毫升刻度线相平时,停止排气。共排气10次。
③如图丙,拔除气针和乳胶管,把排气后的足球放入装满水的容器中,测得溢出水的体积为420毫升。
(1)图乙中,当量筒内外水面都与500毫升刻度线相平时停止排气,其目的是 。
(2)图丙中,足球受到的浮力?
(3)根据测得的数据,计算实验室中空气的密度?
【答案】(1)使量筒内的气压等于外界气压
(2)根据丙图可知,
足球受到的浮力为:F浮=ρ液gV排=103kg/m3×10N/kg×420×10-6m3=4.2N;
(3)甲图中足球受到的浮力:F浮'=ρ液gV排'=103kg/m3×10N/kg×426×10-6m3=4.26N;
则足球的重力为:G=F浮'-F浮=4.26N-4.2N=0.06N;
足球内气体的体积:V=500mL×10=5000mL=5×10-3m3;
则气体的密度:。
【解析】(1)当量筒内外水面相平时,量筒内的气压等于外界大气压强,此时测出气体的体积就是正常情况的体积。
(2)根据阿基米德原理F浮=ρ液gV排计算丙图中足球受到的浮力;
(3)甲和丙中足球受到的浮力之差等于其中气体的重力,而气体的体积等于量筒内排气之和,最后根据密度公式计算气体的密度即可。
【解答】(1)图乙中,当量筒内外水面都与500毫升刻度线相平时停止排气,其目的是:使量筒内的气压等于外界气压。
4.[2021·丽水] 归纳与演绎是科学学习中非常重要的科学方法,下表是兴趣小组归纳“根据ρ=,运用浮力知识间接测量固体密度”的方法,请完成表格。
方法 实验器材 操作过程 思维过程 数据处理 适用范围
一 弹簧测力计、烧杯、水 m=,V物=V排=,ρ物=== ρ物= kg/m3 ρ物>ρ液
二 量筒、细铁丝、水 ……ρ物= ( 用V1、V2、V3、ρ水表示) …… ρ物<ρ液
5.张超同学利用量筒和水测量橡皮泥的密度,请根据图完成下列填空。
(1)在量筒中装适量的水,读出水面对应的刻度值V1= 。
(2)把橡皮泥捏成碗状,小心放入量筒使之漂浮在水面上,读出此时水面对应的刻度值V2,根据漂浮原理可求出橡皮泥的质量m= 。(g取10 N/kg)
(3)再把橡皮泥团成球放入量筒使之沉入水底,读出此时水面对应的刻度值V3。
(4)利用密度计算公式可推导出橡皮泥密度的表达式为ρ= 。由图中读数可算出橡皮泥的密度是 kg/m3。
6.小晨设计了一个用排水法测某实心金属块的密度的实验。实验器材有小空桶、溢水杯、烧杯、量筒和水。实验步骤如下:
①让小空桶漂浮在盛满水的溢水杯中,如图 甲所示;
②将金属块浸没在水中,测得溢出水的体积为20 mL,如图乙所示;
③将烧杯中 20 mL水倒掉,从水中取出金属块,如图丙所示;
④将金属块放入小空桶,小空桶仍漂浮在水面上,测得此时溢出水的体积为 44 mL,如图丁所示。
请回答下列问题:
(1)被测金属块的密度是 g/cm3。(g取10 N/kg)
(2)在实验步骤③和④中,将沾有水的金属块放入小空桶,测出的金属块的密度将 (填“偏大”“不变”或“偏小”)。
4、1.3×103
(1)ρ===3×103 kg/m3;
(2)因为物体漂浮在水中,
所以G=F浮=G排=ρ水(V2-V1)g,
所以m物=m排=ρ水(V2-V1),
物体的体积:V物=V3-V1,
物体的密度:ρ物==。
5.(1)50 cm3 (2)14 g
(4) 1.75×103
6.(1)2.2 (2)不变
考点三、浮力与曲线变化
典例1:(2022八上·余姚期中)将一个底面积为 0.01 m2的长方体木块用细线拴在一个空容器的底部,然后向容器中缓慢加水直到木块上表面与液面相平,如图甲所示。在整个过程中,木块底部受到水的压强随容器中水的深度的变化如图乙所示,则木块所受到的最大浮力为 N,木块重力为 N,细线对木块的最大拉力为 N。
【答案】15;9;6
【解析】(1)由图乙可知,木块恰好漂浮时木块底部受到水的压强,根据求出木块底部受到水向上的压力,根据浮力产生的原因F浮=F向上-F向下求出木块受到的浮力,根据漂浮条件求出木块的重力;
(2)木块浸没时排开水的体积最大,受到的浮力最大,细线对木块的拉力最大,根据图乙读出此时木块底部受到水的压强,根据求出木块底部受到水向上的压力,根据浮力产生的原因F浮=F向上-F向下求出木块受到的最大浮力;
(3)根据二力平衡的知识可知,细线对木块的最大拉力等于最大浮力减去自身的重力。
【解答】(1)由图乙可知,在9cm~16cm内,木块处于漂浮状态,此时木块底部受到水的压强p=900Pa,
由可得,木块底部受到水向上的压力:F向上=p向上S=900Pa×0.01m2=9N,
由浮力产生的原因F浮=F向上-F向下可得,木块受到的浮力:F浮=F向上-F向下=F向上=9N,
因物体漂浮时受到的浮力和自身的重力相等,
所以,木块的重力:G木=F浮=9N;
(2)木块浸没时排开水的体积最大,受到的浮力最大,细线对木块的拉力最大,此时木块下表面所处的深度最大,受到水的压强最大,
由图乙可知,木块上表面与液面相平时,木块底部受到水的压强p′=1500Pa,
此时木块底部受到水向上的压力:F向上′=p向上′S=1500Pa×0.01m2=15N,
木块受到的最大浮力:F浮大=F向上′-F向下=F向上′=15N,
(3)由力的平衡条件可得,细线对木块的最大拉力:F拉大=F浮大-G木=15N-9N=6N。
变式1:(2022八上·鄞州期中)如图甲所示,一个棱长为10cm、重为9N的正方体物块M,水平放置在一个方形容器中,M与容器底部不密合。以恒定水流向容器内注水,容器中水M的深度h随时间t的变化关系如图乙所示,当t=100s时,物块M在水中处于 (选填“沉底”、“悬浮”或“漂浮”)状态,图乙中a的值为 cm。
【答案】漂浮;9
【解析】(1)已知正方体物块M的棱长,由正方体的体积公式可求物块的体积,已知物块的重力可求物块的质量,根据公式可求物块的密度,再与水的密度进行比较,根据物块M的密度小于水的密度,判断物块M最终会漂浮,然后根据图像分析出物块M恰好漂浮的时间点为t=40s,进而判断出t=100s时物块M在水中的状态;
(2)根据物体漂浮条件求出物块M受到的浮力,根据阿基米德原理求出此时物块M排开水的体积,再由V排=SMh浸可求出此时物块浸入水中的深度,即为此时水的深度a的值。
【解答】(1)正方体物块M的体积:V=L3=(10cm)3=1000cm3=0.001m3;
物块M的质量:;
物块M的密度:;
即物块的密度小于水的密度,物块在水中最终会漂浮,
由图象可知,0~40s过程中,随着水的深度逐渐增加,物块M排开水的体积也变大,则物块M所受到水的浮力也变大,
当t=40s时,水的深度变化变慢,说明此时物块M刚好处于漂浮状态,因此当t=100s时,物块M在水中处于漂浮状态;
(2)当t=40s时,物块M刚好处于漂浮状态,则F浮=GM=9N,
根据F浮=ρ水gV排可得此时物块M排开水的体积:,
由V排=SMh浸可得,此时水的深度:。
变式2:(2020八上·奉化期末)如图甲所示,在容器底部固定一轻质弹簧,弹簧受到的拉力跟弹簧的伸长量关系如图乙所示,弹簧上端连有一边长为0.1m的正方体物块A,当容器中水的深度为20cm时,物块A有2/5的体积露出水面,此时弹簧恰好处于自然伸长状态。求:
(1)物块A的密度。
(2)往容器缓慢加水(水未溢出)至物块A恰好浸没时,弹簧的伸长量为多少 再继续加水,木块受到浮力怎么变化
【答案】(1)弹簧恰好处于自然状态时没有发生形变,弹簧对物体没有拉力,物体只受重力和浮力作用,
故F浮=G,即ρ水gV排=ρ物gV,所以ρ物= ρ水= ×1×103kg/m3=0.6×103kg/m3
(2)物块A刚好完全浸没水中时,F浮=ρ水gV=1×103kg/m3×10N/kg×10-3m3=10N
G=mg=ρ物gv=0.6×103kg/m3×10N/kg×10-3m3=6N
弹簧受到的拉力F1=F浮-G=10N-6N=4N
由图乙可知:此时弹簧伸长了4cm
因木块浸没在水中,排开液体体积不变,故浮力不变
【解析】(1)弹簧处于自然伸长状态时,物块不受弹力,那么此时物块受到的浮力等于自身的重力,即F浮=G,用阿基米德原理和密度公式将等式拆开,代入数据计算即可;
(2)当物块A完全浸没时,它受到平衡力,即F浮=G+F弹力;首先根据 F浮=ρ水gV 计算出浮力,再根据 G=mg=ρ物gV计算出它的重力,最后根据前面的关系计算出弹簧的弹力,并根据乙图计算弹簧伸长的长度。
变式3:(2022八上·平阳月考)如图甲所示,一个边长是10cm的立方体木块,下面用一段细线与木块相连,细线另一端固定在容器底(容器高比细线与木块边长之和大得多)。现向容器中慢慢加水,直到细线拉直,如图乙所示。若细线的拉力用F表示,倒入容器中水的深度用h表示(g= 10 N/kg)。
(1)图丙中的A点对应木块在水中的位置是处于 状态。
(2)该木块浸没在水中所受的浮力为多少牛顿?
(3)该木块的密度为多少?
(4)请在丁图中作此过程中木块所受浮力F浮随水的深度h变化的大致图象。
【答案】(1)漂浮
(2)木块的体积:V=10cm×10cm×10cm=1000cm3=1×10-3m3;
木块完全浸没在水中,则V排=V=1×10-3m3;
木块浸没在水中所受的浮力:F浮=ρgV排=1.0×103kg/m3×10N/kg×1×10-3m3=10N;
(3)由题意可知,线拉直后,水还在倒入,所以木块排开水的体积继续增大,浮力增大,则下端线的拉力也相应增大;当木块浸没后,木块排开水的体积不变,浮力不变,则下端线的拉力也不变。
由图象可知,木块浸没时所受拉力最大为4牛,
由力的平衡条件可得F浮=G+F,
所以木块的重力:G=F浮-F=10N-4N=6N,
则木块的质量:
木块的密度:。
(4)
【解析】(1)对物体进行受力分析,当物体不受绳子拉力作用时,物体只受重力和浮力的作用;
(2)已知立方体木块的边长可求得其体积,该木块完全浸没在水中时,V排=V,根据F浮=ρgV排可求出木块浸没在水中的浮力;
(3)由图丙可知浸没时绳子的拉力,根据平衡条件求出木块的重力,根据G=mg求出木块的质量,再利用可求出木块的密度;
(4)分析物体从液面逐渐浸入直到浸没的过程中、木块排开水的体积变化,再根据阿基米德原理F浮=ρ液gV排分析浮力的大小变化。
【解答】(1)根据图丙中的A点对应木块在水中的位置可知,物体只受重力和浮力的作用,绳子对物体的拉力为零,并且物体处于静止状态时,部分体积露出水面,因此此时处于漂浮状态;
(4)①在木块漂浮之前,随着水的深度增大,它排开水的体积增大,根据阿基米德原理F浮=ρ液gV排可知,它受到的浮力逐渐增大;
②当浮力与重力相等时,木块处于漂浮状态。随着水位的升高,木块的位置不断升高,但是浮力保持不变,应该为6N;
③当细线拉直后,木块的位置不能升高,则它排开水的体积继续增大。根据阿基米德原理F浮=ρ液gV排可知,它受到的浮力逐渐增大;
④当木块完全浸没后,它排开水的体积达到最大,此时浮力达到最大为10N。随着水位的升高,它受到的浮力保持不变。如下图所示:
考点四、浮力的受力分析计算
典例1:(2023八上·海曙期末)如图,体积相同的两物体A、B用不可伸长的细线系住,放入水中后,A有四分之一体积露出水面,细线被拉直。已知A重4N,B受到的浮力为8N,A、B密度之比为2:5。那么下列说法正确的是( )
A.A,B所受的重力之比为5:2 B.A、B所受的浮力之比为1:4
C.细线对A的拉力大小为1N D.B对容器底部的压力为零
【答案】D
【解析】(1)由题知,A、B密度之比ρA:ρB=2:5,VA:VB=1:1,利用G=mg=ρVg求A、B所受的重力之比;
(2)A、B的体积相同,都为V,A有四分之一体积露出水面,则A排开水的体积V排A=V,B排开水的体积V排B=V,利用阿基米德原理求A、B所受的浮力之比;
(3)知道B受到的浮力,根据A、B所受的浮力之比可求A受到的浮力,细线对A的拉力大小等于A受到的浮力减去A的重力;
(4)上面求出了A、B的重力之比,知道A的重力,可求B的重力;对B受力分析,求出B对容器底部的压力。
【解答】A.由题知,A、B密度之比ρA:ρB=2:5,VA:VB=1:1,
由G=mg=ρVg可得,A、B所受的重力之比:GA:GB=ρAVAg:ρBVBg=ρA:ρB=2:5,故A错误;
B.已知A、B的体积相同,设均为V,A有四分之一体积露出水面,
则A排开水的体积V排A=V,B排开水的体积V排B=V,
则A、B所受的浮力之比:F浮A:F浮B=ρ水V排Ag:ρ水V排Bg=V:V=3:4,故B错误;
C.由题知,B受到的浮力F浮B=8N,
因F浮A:F浮B=3:4,则A受到的浮力:F浮A=F浮B=×8N=6N,
A受到向上的浮力、向下的重力和拉力,
由力的平衡条件可得细线对A的拉力大小:F拉=F浮A-GA=6N-4N=2N,故C错误;
D.因为GA:GB=2:5,且GA=4N,所以GB=GA=×4N=10N,
B对容器底部的压力:F压=F浮B+F拉-GB=8N+2N-10N=0N,故D正确。
变式1:(2022八上·平阳月考)物体浮在甲液面时有1/5的体积露出液面,物体浮在乙液面时有1/3的体积露出液面,则甲、乙两液体的密度之比是( )
A.5 :12 B.4 :15 C.5 :6 D.12 :5
【答案】C
【解析】根据漂浮条件和阿基米德原理F浮=ρ液gV排分析判断。
【解答】物体在液面漂浮,则它受到的浮力始终等于重力,即浮力相等;
那么:F浮=F浮';
ρ甲gV排甲=ρ乙gV排乙;
ρ甲V排甲=ρ乙V排乙;
那么:.
故选C。
变式2:如图用细线将正方体A和物体B相连放入水中,两物体静止后恰好悬浮,此时A上表面到水面的高度差为0.12m。已知A的体积为1.0×10﹣3m3,所受重力为8N;B的体积为0.5×10﹣3m3,g取10N/kg,求:
(1)A的密度;
(2)细线对B的拉力大小。
【答案】(1)解: mA=GA/g=8N/10N/kg=0.8kg
ρA=mA/VA=0.8kg/1.0×10﹣3m3=0.8×103kg/m3
答:A的密度为0.8×103kg/m3
(2)A受到浮力F浮=ρgV排=1×103kg/m3×10N/kg×1.0×10﹣3m3=10N;因A恰好悬浮所以F浮=GA+F拉A
细线对A的拉力F拉A=F浮﹣GA=10N﹣8N=2N
因为物体间力的作用是相互.的,所以细线对B的拉力F拉B=F拉A=2N。答:细线对B的拉力2N
【解析】(1)首先根据计算物体A的质量,然后再根据计算物体A的密度;
(2)首先根据阿基米德原理计算出A浸没时受到的浮力,然后根据物体A的受力情况:计算细绳对A的拉力,最后根据相互作用力的规律求出细线对B的拉力。
变式3:如图所示,在一个装满水的容器中,轻质弹簧的一端连着小球,另一端固定在容器底部。已知小球的体积是500cm3,小球静止时受到弹簧对它的作用力为4N。则:
(1)此时小球受到的浮力为多少?
(2)如果剪断弹簧后,请分析小球的运动情况,并计算再次静止后小球受到的浮力是多少?
【答案】(1)∵小球完全浸没在水中 ∴V排=V物=500cm3=0.0005m3
F浮=ρ液g V排=1.0×103kg/m3×10N/kg×0.0005m3=5N
(2)解:小球静止时对其进行受力分析可分为二种情况如图所示
由图1可知,G=F浮+F弹=5N+4N=9N
剪断弹簧后,G>F浮 , 小球下沉至容器底部静止,此时F浮=5N
由图2可知,G=F浮-F弹=5N-4N=1N
剪断弹簧后,G<F浮,小球上浮至水面处于飘浮状态,此时F浮=G=1N
【解析】(1)物体浸没时, V排=V物,利用阿基米德原理公式 F浮=ρ液g V排求出 此时小球受到的浮力;(2) 小球静止时对其进行受力分析可分为二种情况:一种情况是 小球下沉至容器底部静止,求出浮力;另一种情况是小球上浮至水面处于飘浮状态。
1.如图,一杯果汁(密度大于水),加冰后液面正好同杯口相平。则在冰块熔化过程中( )
A.液面不变,液体不溢出 B.液面不变,液体溢出 C.液面下降 D.无法确定
【答案】B
【解析】将冰块排开果汁的体积和熔化成水的体积进行比较,如果后者大,那么液体溢出;如果前者大,那么液体不溢出。
冰块在液面上漂浮,那么它受到的浮力等于重力,
即F浮力=G; 那么它排开果汁的体积:;
冰块熔化后质量不变, 那么熔化成水的体积:;
因为ρ水<ρ果汁 , 所以V水>V果汁。
因此液面不变,但是液体溢出。
2.如图所示,容器内有水,有一试管下面挂一小铁块,浮在水面上。现将小铁块取下放入试管中,试管仍浮在水面,则( )
A.液面上升 B.试管底部受到液体的压强变大
C.液面下降 D.试管所受到的浮力不变
【答案】B
【解析】(1)液面上升还是下降,取决于排开水的体积。根据二力平衡的知识比较前后两种状态下受到的总浮力的变化,再根据阿基米德原理F浮=ρ液gV排比较V排的变化,最终确定液面的变化情况;
(2)分析前后两种情况下试管受到浮力的变化,再根据阿基米德原理F浮=ρ液gV排比较试管排开水的体积变化,进而得到试管底部的深度变化,最后根据液体压强公式p=ρ液gh确定试管底部受到压强的变化。
【解答】无论小铁块在试管外,还是在试管内,试管和铁块构成的整体都在水面漂浮,那么它们受到的浮力都等于自身的重力之和。因为它们的重力之和不变,所以受到的浮力不变。根据阿基米德原理F浮=ρ液gV排可知,前后两种情况下排开水的总体积保持不变,自然水面不会发生改变,故A、C错误;
当小铁块在试管外时,铁块也会受到浮力,因此它受到的浮力肯定小于它们受到的总浮力。当小铁块在试管内时,铁块不会受到浮力,因此试管受到的浮力等于它们受到的总浮力。前后比较可知,试管受到的浮力增大了,故D错误;
试管受到的浮力增大,根据阿基米德原理F浮=ρ液gV排可知,试管排开水的体积增大,因此试管底部的深度增大了。根据公式p=ρ液gh可知,试管底部受到液体的压强变大了,故B正确。
3.(2023八上·杭州期末)把一个木球轻轻放入盛满水的溢杯中(足够大),溢出100g水;若将此木球从水中取出,擦干后轻轻放入盛满酒精的溢杯中(足够大),则溢出酒精的质量是(ρ木=0.6×103kg/m3,ρ酒精=0.8×103kg/m3,ρ水=1×103kg/m3)( )
A.大于100g B.等于100g C.小于100g D.无法确定
【答案】B
【解析】将木球的密度与水和酒精的密度进行比较,根据浮沉条件计算它受到的浮力,进而计算出它排开酒精的质量。
【解答】因为木球的密度小于水的密度,所以木球在水中漂浮,那么它受到的浮力等于重力。
因为木球的密度小于酒精的密度,所以木球在酒精中漂浮,那么它受到的浮力等于重力。
比较可知,木球在水中受到的浮力等于在酒精中受到的浮力;
即F浮水=F浮酒;
G排水=G排酒;
m排水g=m排酒;
那么m排酒=m排水=100g。
故选B。
4.(2022八上·杭州期中)将一个物块轻轻放入盛满水的烧杯中,静止后有81克水从烧杯中溢出;将其轻轻放入盛满酒精的烧杯中,静止后有72克酒精从烧杯中溢出。已知酒精密度:0.8×103kg/m3,则该物块在水中的状态及物块的密度分别为( )
A.悬浮 1.0×103kg/m3 B.漂浮 0.9×103kg/m3
C.漂浮 0.92×103kg/m3 D.下沉 1.2×103kg/m3
【答案】B
【解析】分三种情况(大于等于水的密度、大于酒精的密度小于水的密度、小于等于酒精的密度)分析,得出物体的密度大于酒精的密度、小于水的密度,从而确定物体在水中漂浮,根据漂浮条件求出物体重,再根据在酒精中受到的浮力求出物体的体积,利用密度公式求物体的密度。【解答】①假设ρ物≥ρ水,物体将在水中悬浮或下沉在杯底,在酒精中下沉在杯底,此时排开水或酒精的体积相同,根据F浮=ρ液V排g可知受到的浮力关系为5:4,
根据F浮=G排=G溢=m溢g可知浮力关系为9:8,所以ρ物≥ρ水不可行;
②假设ρ物≤ρ酒精,物体将在水中漂浮,在酒精中漂浮或悬浮,这样受到的浮力相等,都等于自重,但是实际受到的浮力不相等,所以ρ物≤ρ酒精不可行;
可见物体的密度一定是大于酒精的密度、小于水的密度,所以物体在水中会漂浮,而在酒精中下沉到杯底:
③因为物体在水中漂浮,漂浮时物体所受浮力等于自身重力,即F浮=G物=m物g,
根据阿基米德原理可知F浮=G排=G溢=m溢g,
所以m物=m溢=81g,
因为物体在酒精中下沉,ρ酒精=0.8×103kg/m3=0.8g/cm3,
所以,
则物体的密度:。
故选B。
5.(2023八上·宁海期末)水平桌面上两个相同的烧杯中分别装有甲、乙两种不同液体,将两个用不同材料制成的正方体A、B(VA<VB),按如图两种方式放入两种液体中,待静止后B刚好浸没在甲液体中,两杯中液面恰好相平。下列说法正确的是( )
A.甲液体的密度大于乙液体的密度
B.甲液体对杯底的压强等于乙液体对杯底的压强
C.甲液体对B下表面的压强等于乙液体对A下表面的压强
D.装甲液体的烧杯对水平桌面的压力小于装乙液体的烧杯对水平桌面的压力
【答案】D
【解析】(1)把A、B两物体作为一个整体,该整体在两液体中都处于漂浮状态,根据漂浮条件可知所受浮力的大小关系;结合题意和图示判断V排的关系,根据F浮=ρ液gV排可比较两种液体的密度关系;
(2)知道两种液体的密度关系,且两杯中液面恰好相平,根据p=ρ液gh分析液体对杯底的压强关系;
(3)根据漂浮条件、浮力产生的原因以及分析液体对物体下表面的压强关系;
(4)先比较两种液体的体积关系和重力关系,再根据”烧杯对水平桌面的压力等于烧杯、物体和液体的总重力“进行分析。
【解答】A、把A、B两物体作为一个整体,由图知,该整体在两液体中都处于漂浮状态,
由漂浮条件可知F浮=GA+GB,所以该整体在两液体中受到的浮力相等;
由图知V排甲=VB,V排乙=VA,且VA<VB,所以V排甲>V排乙;
因整体在两液体中受到的浮力相等,且排开甲液体的体积较大,
由F浮=ρ液gV排可知,两液体的密度关系:ρ甲<ρ乙,故A错误;
B.由题意可知两液体的深度h相同,且ρ甲<ρ乙,由p=ρ液gh可知,甲液体对杯底的压强小于乙液体对杯底的压强,
故B错误;
C.因整体受到的浮力相等(即甲液体中B物体受到的浮力等于乙液体中A物体受到的浮力),且两物体上表面没有受到液体的压力,
所以由浮力产生的原因F浮=F向上-F向下可知,甲液体中B物体与乙液体中A物体的下表面受到的液体压力相等,
由图知B的底面积更大,由可知,甲液体对B下表面的压强小于乙液体对A下表面的压强,故C错误;
D.两烧杯中液面恰好相平且烧杯相同,则液体与物块排开液体的体积之和相同,但V排甲>V排乙,所以甲液体的体积较小。
又知ρ甲<ρ乙,则根据G液=m液g=ρ液gV液可知,甲液体的重力较小;
烧杯对水平桌面的压力F=G杯+GA+GB+G液,因两烧杯相同、其重力相同,且A、B两物体的重力不变,甲液体的重力较小,
所以装甲液体的烧杯对水平桌面的压力较小,
故D正确。
6.(2023八上·宁海期末)迪迪同学将质量为120g的物体放入盛满水的溢水杯中,当物体静止时,溢水杯中溢出了100cm3的水,物体受到的浮力为 N,则此时物体在水中 (选填“漂浮”、“悬浮”或“沉底”).
【答案】1;沉底
【解析】首先根据阿基米德原理F浮=ρ液gV排计算物体受到的浮力,再与重力比较,根据浮沉条件判断物体在水中的状态。
【解答】根据题意可知,
物体在水中受到的浮力:F浮=ρ液gV排=103kg/m3×10N/kg×100×10-6m3=1N;
物体的重力G=mg=0.12kg×10N/kg=1.2N;
即浮力小于重力,
那么物体在水中沉底。
7.(2022八上·富阳期中)小科按照教材中"综合实践活动"的要求制作简易密度计。
(1)取一根粗细均匀的饮料吸管,在其下端塞入适量金属丝并用石蜡封口。塞入金属丝的目的是使吸管能漂浮在液体中。这根吸管竖直漂浮在不同液体中时,液体密度越大,它露出液面部分的长度 (选填“越长”、“越短”或“”不变”)
(2)小科根据图甲在吸管上标出1.0刻度线(单位g/cm , 下同),再利用上述关系式进行计算,标出了0.9、1.0、1.1的刻度线,如图乙A,B,C,D所示,则标示正确的图是
(3)将吸管放到水中的情境如丙图(a)所示,测得浸入的长度为H;放到另一液体中的情景如丙图(b)所示,浸入的长度为h。用ρ液、ρ水分别表示液体和水的密度,则h和ρ水、ρ液,H的关系式是h= 。
【答案】(1)越长
(2)C
(3)
【解析】(1)根据浮沉条件和阿基米德原理F浮=ρ液gV排分析即可;
(2)根据阿基米德原理F浮=ρ液gV排分析吸管上刻度随液体密度的变化规律即可;
(3)根据浮沉条件和阿基米德原理F浮=ρ液gV排推导计算即可。
【解答】(1)密度计始终漂浮在液面上,则它受到的浮力始终等于重力,即浮力保持不变。
根据阿基米德原理F浮=ρ液gV排可知,当液体密度增大时,密度计排开液体的体积减小;
根据V露=V-V排可知,它露出液面的部分长度越大。
(2)根据阿基米德原理F浮=ρ液gV排=ρ液gSh排可知,液面的密度与密度计浸入的深度成反比,即液体密度越大,浸入深度越小,而此时刻度越靠下,那么从上到下,密度计上的刻度值越来越大,且越往下刻度越密集,故选C。
(3)根据丙图可知,密度计受到的浮力相等;
即Fa=Fb;
ρ水gV排=ρ液gV排;
ρ水gSH=ρ液gSh;
ρ水H=ρ液h;
解得:。
8.(2023八上·义乌期末)小明利用电子秤、长方体铁块、细线、圆柱形玻璃板、糖水,探究“影响浮力大小的因素”实验。
(1)如图甲,将搅拌均匀的糖水装入柱形杯中,置于电子秤上,示数为400.0g。用质量和体积均不计的细线系好铁块,缓慢浸入装有糖水的容器中,直到乙图所示的位置,发现该过程中电子秤示数逐渐增大。说明:铁块所受浮力大小与
有关;
(2)继续将铁块缓慢浸没到图丙所示位置,通过观察与比较,小明认为物体所受浮力大小与浸没后的深度
(选填“有关”或“无关”);
(3)将铁块沉入杯底,松开细线(细线已松弛),此时电子秤的示数如图丁所示,糖水密度为
kg/m3;(铁的密度是7.9克/厘米3)
(4)放置一段时间后,将铁块从糖水中慢慢提起。小明发现铁块离开杯底至上表面露出液面前,电子秤示数逐渐减小,造成这种现象的主要原因可能是
。
【答案】(1)排开液体的体积
(2)无关
(3)1.12×103
(4)放置一段时间后糖水密度不均匀
【解析】(1)电子秤的示数增大,说明铁块受到的浮力增大,分析缓慢入水过程中影响浮力的哪个因素发生改变即可。
(2)当深度增大时,如果电子秤的示数发生改变,那么说明浮力大小与浸没深度有关;否则,二者无关。
(3)甲和丁的示数之差等于铁块的质量,根据公式计算铁块的体积,也就是铁块排开糖水的体积,最后根据计算糖水密度即可。
(4)电子秤的示数逐渐减小,说明铁块受到的浮力逐渐减小,而它排开糖水的体积不变,根据阿基米德原理F浮=ρ液gV排可知,肯定是糖水的密度发生了变化,据此分析解答。
【解答】(1)在铁块缓慢浸入糖水中时,它排开糖水的体积不断增大,而电子秤的示数增大说明它受到的浮力增大,那么得到结论:铁块所受浮力大小与排开液体的体积有关。
(2)继续将铁块缓慢浸没到图丙所示位置,它浸没的深度不断增大,但是电子秤的示数保持不变,说明它受到的浮力不变,那么得到结论:物体所受浮力大小与浸没后的深度无关。
(3)根据甲、丁可知,铁块的质量为:m铁=558g-422.4g=135.6g;
则铁块的体积为:;
甲和乙的示数之差等于铁块排开糖水的质量:m排=422.4g-400g=22.4g;
则糖水的密度:。
(4)小明发现铁块离开杯底至上表面露出液面前,电子秤示数逐渐减小,造成这种现象的主要原因可能是:放置一段时间后糖水密度不均匀。
9.(2020八上·余杭月考)人们常用“冰山一角"来形容事物显露出来的仅仅是其很小的部分,更多的还隐藏在表面现象之下。事实上,冰山浮在海水中的确只露”一角"(如图所示)。若现有一座冰山,它露出海面的体积是2000m3 , (已知:海水的密度取ρ海水=1×103kg/m3 , 冰的密度ρ冰=0.9×103kg/m3)。则:
(1)假如此冰山完全熔化,则液面将________(填“不变”、“降低”或“上升");
(2)这座冰山的总体积为多少?
【答案】(1)不变
(2)冰山在海面漂浮,那么得到:
F浮=G;
ρ水gV排=ρ冰gV;
ρ水V排=ρ冰V;
103kg/m3×(V-2000m3)=0.9×103kg/m3×V;
解得:V=20000m3。
【解析】(1)冰熔化成水质量不变,根据密度公式计算出熔化成水的体积,根据阿基米德原理计算出冰山在海水中的V排 , 然后二者比较即可;
(2)首先根据漂浮条件列出浮力和重力的关系式,然后根据密度公式和阿基米德原理将公式拆开,代入数据计算出冰山的体积即可。
【解答】(1)冰山在海水表面漂浮,那么它受到的浮力等于重力,
它排开海水的体积:;
冰山熔化后,水的体积为:;
因为熔化前后,冰山的重力G不变,且海水的密度等于淡水密度,
所以V排=V;
因此冰山完全熔化受,液面会不变。
(2)冰山在海面漂浮,那么得到:
F浮=G;
ρ水gV排=ρ冰gV;
ρ水V排=ρ冰V;
103kg/m3×(V-2000m3)=0.9×103kg/m3×V;
解得:V=20000m3。
10.(2022八上·鹿城月考)小华发现用密度计测量液体密度需要大量液体,因此他用家里闲置的眼镜盒自制了密度计,该自制密度计高为16厘米,横截面积为20cm2,在盒子底部加入沙子使密度计能竖立水中,密度计自重200克。使用时烧杯中装有一定量的水。求:
(1)未放入待测液体之前,该密度计所受浮力多大
(2)往密度计中放入10毫升待测液,密度计浸入深度为10.6cm,则待测液的密度为多少
(3)为了提高自制密度计的精确度,请提出一条改进建议:
【答案】(1)∵漂浮
∴F浮=G=mg=0.2kg×10N/kg=2N
(2)∵F 浮’=ρ水gV 排’=103kg/m3×10N/kg×2×10-3m2×0.106m=2.12N
∴G 液=F 浮’-G=2.12N-2N=0.12N
∴
(3)将烧杯中的水换成密度更小的液体;减小密度计的横截面积;增加待测液的体积等
【解析】(1)当物体漂浮时,它受到的浮力等于重力,据此计算密度计受到的浮力;
(2)首先根据阿基米德原理F浮力=ρ液gV排计算出此时密度计受到的浮力,再根据二力平衡的知识计算出里面液体的重力,根据计算出里面液体的质量,最后利用密度公式计算液体密度。
(3)在测量液体密度时,密度计排开液体的体积越大,则浸入液体中的高度变化越大,那么密度计越精确,根据阿基米德原理F浮力=ρ液gV排分析即可。
【解答】(3)根据阿基米德原理F浮力=ρ液gV排=ρ液gSh排可知,要增大h排,可以减小液烧杯中液体的密度,或者减小密度计的横截面积,还可以增大待测液体的体积,从而增大浮力,进而增大h排。
11.(2022八上·慈溪月考)如图甲所示,水平放置的方形容器里有一个重为9 N、边长为10 cm的立方体物块M,M与容器底部不密合。以6 mL/s的恒定水流向容器内注水,容器中水的深度h随时间t的变化关系如图乙所示。求:
(1)当t=100 s时,物块M在水中处于 (选填“沉底”“悬浮"或“漂浮”)状态。
(2)当t=100 s时,水对容器底部的压力大小是多少
(3)图乙中a的值是多少
【答案】(1)漂浮
(2)当t=100s时,注入的水的体积V水=vt=6mL/s×100s=600mL=6×10-4m3,
则G水=ρ水gV水=1.0×103kg/m3×10N/kg×6×10-4m3=6N;
所以液体对底部的压力F=G水+GM=6N+9N=15N;
(3)当t=40s时,正好是物块M处于刚刚开始漂浮的状态,则F浮=GM=9N,
根据F浮=ρ液gV排可得:;
所以深度。
【解析】(1)已知物块M的边长,可求物块的体积,已知物块的重力可求物块的质量,根据密度公式可求物块的密度,再与水的密度进行比较,即可知道物体的在水中的浮沉状态;
(2)由于方形容器在水平方向上放置,则液体对底部的压力等于容器里液体和漂浮物体的总重力,所以根据V=vt求出当t=100s时注入的水的体积,然后求出水的重力,最后根据F=G水+GM即可求出压力;
(3)由乙可知:t=40s时,水的深度变化改变,即此时正好是物块M处于刚刚开始漂浮的状态,所以根据阿基米德原理F浮=ρ液gV排求出此时物块浸入水中的体积,最后根据计算出a的值。【解答】(1)物块M的体积V=(0.1m)3=0.001m3;
物块M的质量:;
物块M的密度;
即物块的密度小于水的密度,
根据图像可知,从40s~140s时,水面上升的速度减小,
即此时应该是物块离开容器底部,
那么当t=100s时,物体应该处于漂浮状态。
12.(2022八上·长兴月考)边长为10cm的正方体物块放入水平桌面上的圆柱形容器底部(如图甲所示),逐渐向容器内倒入适量水(水未溢出),测量容器内水的深度h,分别计算出物块对应受到的浮力F浮,并绘制了如图乙(实线)所示的图象。把水换成液体A重复上述实验,绘制了如图乙(虚线)所示的图像。
(1)由图乙可知,正方体物块受到的重力为 N。
(2)正方体物块的密度为多少?
(3)液体A的密度为多少?
【答案】(1)9
(2)正方体物块的体积V=L3=(10cm)3=1000cm3=0.001m3,
物体的密度:;
(3)由图象可知,当h=10cm以后物体在液体中受到的浮力F浮′=6N不变,
因F浮′<G,所以,物体处于沉底状态,
因物体完全浸没时排开液体的体积和自身的体积相等,
由F浮=ρ液gV排可得液体的密度为:。
【解析】(1)根据正方体物块的边长和水的深度从h=9cm以后物体受到的浮力9N不再发生变化,判断出物体的状态;物体处于漂浮状态时,受到的浮力和重力相等;
(2)知道边长可求体积,根据求出物体的密度;
(3)从图象中读出h=10cm以后物体在液体中受到的浮力,比较物体的重力和受到的浮力判断物体的状态,根据阿基米德原理F浮=ρ液gV排求出液体的密度。
【解答】(1)正方体物块的边长为10cm,由图象可知,水的深度从h=9cm以后物体受到的浮力9N不再发生变化,说明物体处于漂浮状态;
因物体漂浮时,受到的浮力和重力相等,
所以,物体的重力G=F浮=9N;
13.(2022八上·瑞安期中)某科学兴趣小组自制了一架简易液体密度计,使用说明书如下:
简易液体密度计使用说明书
结构 使用方法:1.弹簧测力计左边表示测力计示数,右边表示相应液体密度示数。2.将小金属块用细线挂于测力计挂钩处,测力计的示数为2牛,密度计的标记数值为0。3.将小金属块完全浸没于待测液体中。4.在右边刻度板上读出相应密度值。
(1)当金属块下表面刚好接触水面并下降,下列图中能正确反映这一过程中浮力F 和小金属 块下表面到水面距离h 的关系的图象是
A. B.
C. D.
(2)将小金属块(重为2牛,体积为40立方厘米)浸没在某种液体中时,左边测力计示数为1牛,则对应右边的密度值是多少千克/立方米?(写出计算过程)
(3)若将小金属块(重为2牛,体积为40立方厘米)换成大金属块(重5牛,体积为80立方厘米),已知两金属块材质不同,判断该密度计的量程和精确度将如何改变,并说明理由。
【答案】(1)D
(2)当金属块浸没时,其所受的浮力为:F浮=G-F拉==2牛-1牛=1牛(1分)
V排=V物=40厘米3=4x10-5米3
ρ=F浮/gV排=1牛/10牛/千克x4x10-5米3=2.5x103千克/米3
(3)精确度变大,量程变大。物块悬浮时,物块密度和液体密度相同,此时密度最大即为量程,由数据可知,大物块密度大,所以量程变大。根据F浮=G-F拉=G-p液gV排,当拉力变化量相同时,大物块比小物块体积大,V,变化量也大,所测液体密度的变化量小,所以精确度高。
【解析】(1)根据阿基米德原理F浮=ρ液gV排分析金属块受到浮力的变化;
(2)首先根据 F浮=G-F拉 计算出金属块受到的浮力,再根据阿基米德原理的变形式计算液体的密度。
(3)根据浮沉条件分析密度计量程的变化,根据“称量法” F浮=G-F拉 结合阿基米德原理F浮=ρ液gV排分析密度计分度值的变化,从而确定精确度的变化。
【解答】(1)随着金属块慢慢浸入水中时,它排开水的体积不断增大;当它完全浸没在水中时,它排开水的体积不变。根据阿基米德原理F浮=ρ液gV排可知,金属块受到的浮力先变大后不变。
典例分析
举一反三
典例分析
举一反三
典例分析
举一反三
典例分析
举一反三
课后巩固
考点一、液面高度变化的问题
液面变化问题主要可以总结为关于V排变化的分析。相对简单的试题只要把握好这一点即可。
将物体浸入(移出)柱形容器的液体中(如图1),若物体排开液体的体积为V排,容器的横截面积为S底,则物体浸入(移出)前后液面高度的变化量为=
浸入柱形容器中的柱形物体高出液面(如图2),当向容器中注入液体V加后,液面高度=
图1 图2 图3 图4
关于“冰化水”与“船载”问题
一块冰浮于水面,如图3那么当冰熔化前后,其水面将 (选填“升高”、“降低” 或“不变”)
证明:冰熔化前:由于漂浮,F浮=G物。则V排 = m冰g/ρ水g = m冰/ρ水。
冰熔化:由于m水= m冰,由ρ=m/V得 V化水=m水/ρ水=m冰/ρ水。
因 V排水= V化水,即冰熔化成水后,刚好填满原来被冰排开的水的体积,因此,水面保持不变。
① 若上题中的冰包含有气泡,则冰熔化后液面将如何变
② 若上题中的冰包有一小木块(ρ物<ρ水),则冰熔化后液面又将如何
③ 若上题中的冰包含有一小石块(ρ物>ρ水)则冰熔化后又如何
(2)如图4,铁块A叠放在木块B上,然后放在水缸中当将铁块从木块上拿下,并放在水缸底部时,水面高度将 。
二、如何用浮力知识来测固体或液体的密度
(1)测固体的密度
[例一] 请利用弹簧测力计、水、烧杯测出一块小石头(ρ物>ρ水)的密度。
① 实验原理 F浮=G-F拉 (称重法)
② 步骤:a 用弹簧测力计先测出小石块在空气中的重力记为G石,进而得出m石;
b 用弹簧测力计悬吊着小石块,使之浸没在水杯中。并记下此时弹簧测力计的示数为F拉;
c 由F浮+F拉=G可求得小石块浸没在水中受到的浮力为F浮=G石-F拉,由F浮=ρ液gV排得,算出V排;
d 由F浮=ρ液gV排和G=mg=ρ物gV物及V物=V排得ρ石= ρ水。
[例二] 利用量筒、水、细针测出不沉于水的蜡块密度(ρ物<ρ水)。
① 实验原理 F浮=G(漂浮法)
② 步骤:a 先往量筒中倒入适量的水,记下水的体积为V0;
b 然后往量筒中放入小蜡块,待小蜡块静止后,记下水面现在所对应的刻度为V1,即蜡块漂浮时V排=V1-V0;
c 用细针将蜡块全部按入水中,记下现在水面刻度为V2,此时蜡块的体积为V蜡=V2-V0;
d 利用漂浮条件F浮=G,即ρ水gV排=ρ蜡gV蜡得出ρ蜡=ρ水。
(2)测液体的密度
[方法一] 原理:F浮=G-F拉和F浮=ρ液gV排。(称重法)
器材:弹簧测力计、烧杯、适量的水、适量的待测液体和一个密度大于水和液体的物体。
过程:用上述器材分别测出物体在水中和待测液体中的浮力,则有
即:ρ液=。
[方法二]原理:F浮=G物(漂浮法)
器材:量筒、水和待测液体、一个密度比水和待测液体小的物体。
过程:用上述器材分别测出物体在水中和待测液体中的V排即可,即:由G物=F浮水和G物=F浮液可知ρ水gV排水=ρ液gV排液,也即ρ液=。
考点一、液面高度变化的问题
典例1:(2022八上·镇海期末)如图所示,一块冰放在盛有的水的容器中,已知冰块与容器底部相接触并相互间有压力,则当冰完全融化成水后,容器中水面的位置将 。
变式1:(2023八上·杭州期末)小金发现一冰块内有小石块,测得总质量是200g,放在水槽中,恰好悬浮在水中,则冰块与小石块的总体积是 cm3。当冰熔化后小石块沉入了水槽底,此时水槽中的水面 (选填“上升”、“下降”或“不变”)。(ρ水=1×103kg/m3,ρ冰=0.9×103kg/m3)
变式2:(2022八上·余姚期末)如图所示,在一个足够深的水槽中漂浮着一个木杯,此时杯口到水面的垂直距离为h,水槽底部到水面的垂直距离为H,若从水槽中取少量水倒入木杯中,则h (填“变大”,“变小”或“不变”,下同),H 。
(2) (3)
变式3:(2022·浙江台州·八年级期末)小金把家里景观水池底部的鹅卵石取出清洗,他先将一个重为15N的空桶漂浮在水面上,然后将池底的鹅卵石捞出放置在桶内,桶仍漂浮在水面(不考虑捞出过程中带出的水,ρ水=1.0×103kg/m3)
(1)某块鹅卵石在水池底部时,它受到的浮力 它的重力(选填“大于”、“小于”或“等于”)。
(2)全部鹅卵石捞出放置在桶内时,水池内水面高度与鹅卵石未捞出时相比会_______(选填“上升”、“下降”或“不变”)。若此时桶排开水的体积为5.0×10-3m3,求桶内鹅卵石的总质量。
考点二、利用浮力测物体密度
典例1:(2022八上·宁海期中)小明用装有适量水的薄壁小试管、螺母和细线制成一个测量小石块密度的装置。将此装置放入水中静止时,试管署出水面的高度h1为5cm,如图甲所示:在试管中轻轻放入小石块,装夏在水中静止时,试管露出水面的高度h2为2cm,如图乙所示。已知小石块放入试管前后.试管中的液面差h3为2cm。则
(1)小试管所受浮力的方向为
(2)石块的密度为 kg/m3
变式1:下面是小金利用量筒和水测量橡皮泥密度的实验操作情景,
(1)乙图中橡皮泥受到的浮力为______牛。
(2)由图中读数可算出橡皮泥的密度是______kg/m3。
变式2:(2023八上·椒江期末)小科在验证阿基米德原理时,利用溢水杯、弹簧测力计、铁块、小桶、细线等进行实验,具体操作步骤如图:
(1)细心的同学发现图乙步骤中存在错误,请指出该错误是: 。如果不加改正,会导致浮力F浮 (选填“大于”、“等于”或“小于”)排开水的重力G排。
(2)纠正错误后,若图中测得的F1、F2、F3、F4关系满足 ,则阿基米德原理得到验证。
(3)实验后,小科发现利用实验所得数据还能测出所用铁块的密度,ρ铁= (水的密度用ρ水表示)。
变式3:(2023八上·鄞州期末)气体的密度与压强有关。为测量实验室内空气的密度,小明在实验室按如图所示步骤进行实验:
①如图甲,将一打足气的足球,放入装满水的容器中,测得溢出水的体积为426毫升。
②如图乙,将500毫升装满水的量筒倒置于水槽中,用气针和乳胶管将足球中的气体慢慢排入该量筒,同时调整量筒的位置,当量筒内外水面都与500毫升刻度线相平时,停止排气。共排气10次。
③如图丙,拔除气针和乳胶管,把排气后的足球放入装满水的容器中,测得溢出水的体积为420毫升。
(1)图乙中,当量筒内外水面都与500毫升刻度线相平时停止排气,其目的是 。
(2)图丙中,足球受到的浮力?
(3)根据测得的数据,计算实验室中空气的密度?
4.[2021·丽水] 归纳与演绎是科学学习中非常重要的科学方法,下表是兴趣小组归纳“根据ρ=,运用浮力知识间接测量固体密度”的方法,请完成表格。
方法 实验器材 操作过程 思维过程 数据处理 适用范围
一 弹簧测力计、烧杯、水 m=,V物=V排=,ρ物=== ρ物= kg/m3 ρ物>ρ液
二 量筒、细铁丝、水 ……ρ物= ( 用V1、V2、V3、ρ水表示) …… ρ物<ρ液
5.张超同学利用量筒和水测量橡皮泥的密度,请根据图完成下列填空。
(1)在量筒中装适量的水,读出水面对应的刻度值V1= 。
(2)把橡皮泥捏成碗状,小心放入量筒使之漂浮在水面上,读出此时水面对应的刻度值V2,根据漂浮原理可求出橡皮泥的质量m= 。(g取10 N/kg)
(3)再把橡皮泥团成球放入量筒使之沉入水底,读出此时水面对应的刻度值V3。
(4)利用密度计算公式可推导出橡皮泥密度的表达式为ρ= 。由图中读数可算出橡皮泥的密度是 kg/m3。
6.小晨设计了一个用排水法测某实心金属块的密度的实验。实验器材有小空桶、溢水杯、烧杯、量筒和水。实验步骤如下:
①让小空桶漂浮在盛满水的溢水杯中,如图 甲所示;
②将金属块浸没在水中,测得溢出水的体积为20 mL,如图乙所示;
③将烧杯中 20 mL水倒掉,从水中取出金属块,如图丙所示;
④将金属块放入小空桶,小空桶仍漂浮在水面上,测得此时溢出水的体积为 44 mL,如图丁所示。
请回答下列问题:
(1)被测金属块的密度是 g/cm3。(g取10 N/kg)
(2)在实验步骤③和④中,将沾有水的金属块放入小空桶,测出的金属块的密度将 (填“偏大”“不变”或“偏小”)。
考点三、浮力与曲线变化
典例1:(2022八上·余姚期中)将一个底面积为 0.01 m2的长方体木块用细线拴在一个空容器的底部,然后向容器中缓慢加水直到木块上表面与液面相平,如图甲所示。在整个过程中,木块底部受到水的压强随容器中水的深度的变化如图乙所示,则木块所受到的最大浮力为 N,木块重力为 N,细线对木块的最大拉力为 N。
变式1:(2022八上·鄞州期中)如图甲所示,一个棱长为10cm、重为9N的正方体物块M,水平放置在一个方形容器中,M与容器底部不密合。以恒定水流向容器内注水,容器中水M的深度h随时间t的变化关系如图乙所示,当t=100s时,物块M在水中处于 (选填“沉底”、“悬浮”或“漂浮”)状态,图乙中a的值为 cm。
变式2:(2020八上·奉化期末)如图甲所示,在容器底部固定一轻质弹簧,弹簧受到的拉力跟弹簧的伸长量关系如图乙所示,弹簧上端连有一边长为0.1m的正方体物块A,当容器中水的深度为20cm时,物块A有2/5的体积露出水面,此时弹簧恰好处于自然伸长状态。求:
(1)物块A的密度。
(2)往容器缓慢加水(水未溢出)至物块A恰好浸没时,弹簧的伸长量为多少 再继续加水,木块受到浮力怎么变化
变式3:(2022八上·平阳月考)如图甲所示,一个边长是10cm的立方体木块,下面用一段细线与木块相连,细线另一端固定在容器底(容器高比细线与木块边长之和大得多)。现向容器中慢慢加水,直到细线拉直,如图乙所示。若细线的拉力用F表示,倒入容器中水的深度用h表示(g= 10 N/kg)。
(1)图丙中的A点对应木块在水中的位置是处于 状态。
(2)该木块浸没在水中所受的浮力为多少牛顿?
(3)该木块的密度为多少?
(4)请在丁图中作此过程中木块所受浮力F浮随水的深度h变化的大致图象。
考点四、浮力的受力分析计算
典例1:(2023八上·海曙期末)如图,体积相同的两物体A、B用不可伸长的细线系住,放入水中后,A有四分之一体积露出水面,细线被拉直。已知A重4N,B受到的浮力为8N,A、B密度之比为2:5。那么下列说法正确的是( )
A,B所受的重力之比为5:2
B.A、B所受的浮力之比为1:4
C.细线对A的拉力大小为1N
D.B对容器底部的压力为零
变式1:(2022八上·平阳月考)物体浮在甲液面时有1/5的体积露出液面,物体浮在乙液面时有1/3的体积露出液面,则甲、乙两液体的密度之比是( )
A.5 :12 B.4 :15 C.5 :6 D.12 :5
变式2:如图用细线将正方体A和物体B相连放入水中,两物体静止后恰好悬浮,此时A上表面到水面的高度差为0.12m。已知A的体积为1.0×10﹣3m3,所受重力为8N;B的体积为0.5×10﹣3m3,g取10N/kg,求:(1)A的密度;
(2)细线对B的拉力大小。
变式3:如图所示,在一个装满水的容器中,轻质弹簧的一端连着小球,另一端固定在容器底部。已知小球的体积是500cm3,小球静止时受到弹簧对它的作用力为4N。则:
(1)此时小球受到的浮力为多少?
(2)如果剪断弹簧后,请分析小球的运动情况,并计算再次静止后小球受到的浮力是多少?
课后巩固
1.如图,一杯果汁(密度大于水),加冰后液面正好同杯口相平。则在冰块熔化过程中( )
A.液面不变,液体不溢出 B.液面不变,液体溢出 C.液面下降 D.无法确定
(1) (2) (3)
2.如图所示,容器内有水,有一试管下面挂一小铁块,浮在水面上。现将小铁块取下放入试管中,试管仍浮在水面,则( )
A.液面上升 B.试管底部受到液体的压强变大
C.液面下降 D.试管所受到的浮力不变
5.(2023八上·宁海期末)水平桌面上两个相同的烧杯中分别装有甲、乙两种不同液体,将两个用不同材料制成的正方体A、B(VA<VB),按如图两种方式放入两种液体中,待静止后B刚好浸没在甲液体中,两杯中液面恰好相平。下列说法正确的是( )
A.甲液体的密度大于乙液体的密度
B.甲液体对杯底的压强等于乙液体对杯底的压强
C.甲液体对B下表面的压强等于乙液体对A下表面的压强
D.装甲液体的烧杯对水平桌面的压力小于装乙液体的烧杯对水平桌面的压力
3.(2023八上·杭州期末)把一个木球轻轻放入盛满水的溢杯中(足够大),溢出100g水;若将此木球从水中取出,擦干后轻轻放入盛满酒精的溢杯中(足够大),则溢出酒精的质量是(ρ木=0.6×103kg/m3,ρ酒精=0.8×103kg/m3,ρ水=1×103kg/m3)( )
A.大于100g B.等于100g C.小于100g D.无法确定
4.(2022八上·杭州期中)将一个物块轻轻放入盛满水的烧杯中,静止后有81克水从烧杯中溢出;将其轻轻放入盛满酒精的烧杯中,静止后有72克酒精从烧杯中溢出。已知酒精密度:0.8×103kg/m3,则该物块在水中的状态及物块的密度分别为( )
A.悬浮 1.0×103kg/m3 B.漂浮 0.9×103kg/m3
C.漂浮 0.92×103kg/m3 D.下沉 1.2×103kg/m3
6.(2023八上·宁海期末)迪迪同学将质量为120g的物体放入盛满水的溢水杯中,当物体静止时,溢水杯中溢出了100cm3的水,物体受到的浮力为 N,则此时物体在水中 (选填“漂浮”、“悬浮”或“沉底”).
7.(2022八上·富阳期中)小科按照教材中"综合实践活动"的要求制作简易密度计。
(1)取一根粗细均匀的饮料吸管,在其下端塞入适量金属丝并用石蜡封口。塞入金属丝的目的是使吸管能漂浮在液体中。这根吸管竖直漂浮在不同液体中时,液体密度越大,它露出液面部分的长度 (选填“越长”、“越短”或“”不变”)
(2)小科根据图甲在吸管上标出1.0刻度线(单位g/cm , 下同),再利用上述关系式进行计算,标出了0.9、1.0、1.1的刻度线,如图乙A,B,C,D所示,则标示正确的图是
(3)将吸管放到水中的情境如丙图(a)所示,测得浸入的长度为H;放到另一液体中的情景如丙图(b)所示,浸入的长度为h。用ρ液、ρ水分别表示液体和水的密度,则h和ρ水、ρ液,H的关系式是h= 。
8.(2023八上·义乌期末)小明利用电子秤、长方体铁块、细线、圆柱形玻璃板、糖水,探究“影响浮力大小的因素”实验。
(1)如图甲,将搅拌均匀的糖水装入柱形杯中,置于电子秤上,示数为400.0g。用质量和体积均不计的细线系好铁块,缓慢浸入装有糖水的容器中,直到乙图所示的位置,发现该过程中电子秤示数逐渐增大。说明:铁块所受浮力大小与
有关;
(2)继续将铁块缓慢浸没到图丙所示位置,通过观察与比较,小明认为物体所受浮力大小与浸没后的深度
(选填“有关”或“无关”);
(3)将铁块沉入杯底,松开细线(细线已松弛),此时电子秤的示数如图丁所示,糖水密度为
kg/m3;(铁的密度是7.9克/厘米3)
(4)放置一段时间后,将铁块从糖水中慢慢提起。小明发现铁块离开杯底至上表面露出液面前,电子秤示数逐渐减小,造成这种现象的主要原因可能是
。
9.(2020八上·余杭月考)人们常用“冰山一角"来形容事物显露出来的仅仅是其很小的部分,更多的还隐藏在表面现象之下。事实上,冰山浮在海水中的确只露”一角"(如图所示)。若现有一座冰山,它露出海面的体积是2000m3 , (已知:海水的密度取ρ海水=1×103kg/m3 , 冰的密度ρ冰=0.9×103kg/m3)。则:
(1)假如此冰山完全熔化,则液面将________(填“不变”、“降低”或“上升");
(2)这座冰山的总体积为多少?
10.(2022八上·鹿城月考)小华发现用密度计测量液体密度需要大量液体,因此他用家里闲置的眼镜盒自制了密度计,该自制密度计高为16厘米,横截面积为20cm2,在盒子底部加入沙子使密度计能竖立水中,密度计自重200克。使用时烧杯中装有一定量的水。求:
(1)未放入待测液体之前,该密度计所受浮力多大
(2)往密度计中放入10毫升待测液,密度计浸入深度为10.6cm,则待测液的密度为多少
(3)为了提高自制密度计的精确度,请提出一条改进建议:
11.(2022八上·慈溪月考)如图甲所示,水平放置的方形容器里有一个重为9 N、边长为10 cm的立方体物块M,M与容器底部不密合。以6 mL/s的恒定水流向容器内注水,容器中水的深度h随时间t的变化关系如图乙所示。求:
(1)当t=100 s时,物块M在水中处于 (选填“沉底”“悬浮"或“漂浮”)状态。
(2)当t=100 s时,水对容器底部的压力大小是多少
(3)图乙中a的值是多少
12.(2022八上·长兴)边长为10cm的正方体物块放入水平桌面上的圆柱形容器底部(如图甲所示),逐渐向容器内倒入适量水(水未溢出),测量容器内水的深度h,分别计算出物块对应受到的浮力F浮,并绘制了如图乙(实线)所示的图象。把水换成液体A重复上述实验,绘制了如图乙(虚线)所示的图像。
(1)由图乙可知,正方体物块受到的重力为 N。
(2)正方体物块的密度为多少?
(3)液体A的密度为多少?
第3节 水的浮力3-重难点培优
考点一、液面高度变化的问题
液面变化问题主要可以总结为关于V排变化的分析。相对简单的试题只要把握好这一点即可。
将物体浸入(移出)柱形容器的液体中(如图1),若物体排开液体的体积为V排,容器的横截面积为S底,则物体浸入(移出)前后液面高度的变化量为=
浸入柱形容器中的柱形物体高出液面(如图2),当向容器中注入液体V加后,液面高度=
图1 图2 图3 图4
关于“冰化水”与“船载”问题
一块冰浮于水面,如图3那么当冰熔化前后,其水面将 (选填“升高”、“降低” 或“不变”)
证明:冰熔化前:由于漂浮,F浮=G物。则V排 = m冰g/ρ水g = m冰/ρ水。
冰熔化:由于m水= m冰,由ρ=m/V得 V化水=m水/ρ水=m冰/ρ水。
因 V排水= V化水,即冰熔化成水后,刚好填满原来被冰排开的水的体积,因此,水面保持不变。
① 若上题中的冰包含有气泡,则冰熔化后液面将如何变
② 若上题中的冰包有一小木块(ρ物<ρ水),则冰熔化后液面又将如何
③ 若上题中的冰包含有一小石块(ρ物>ρ水)则冰熔化后又如何
(2)如图4,铁块A叠放在木块B上,然后放在水缸中当将铁块从木块上拿下,并放在水缸底部时,水面高度将
知识点 不变 降低
二、如何用浮力知识来测固体或液体的密度
(1)测固体的密度
[例一] 请利用弹簧测力计、水、烧杯测出一块小石头(ρ物>ρ水)的密度。
① 实验原理 F浮=G-F拉 (称重法)
② 步骤:a 用弹簧测力计先测出小石块在空气中的重力记为G石,进而得出m石;
b 用弹簧测力计悬吊着小石块,使之浸没在水杯中。并记下此时弹簧测力计的示数为F拉;
c 由F浮+F拉=G可求得小石块浸没在水中受到的浮力为F浮=G石-F拉,由F浮=ρ液gV排得,算出V排;
d 由F浮=ρ液gV排和G=mg=ρ物gV物及V物=V排得ρ石= ρ水。
[例二] 利用量筒、水、细针测出不沉于水的蜡块密度(ρ物<ρ水)。
① 实验原理 F浮=G(漂浮法)
② 步骤:a 先往量筒中倒入适量的水,记下水的体积为V0;
b 然后往量筒中放入小蜡块,待小蜡块静止后,记下水面现在所对应的刻度为V1,即蜡块漂浮时V排=V1-V0;
c 用细针将蜡块全部按入水中,记下现在水面刻度为V2,此时蜡块的体积为V蜡=V2-V0;
d 利用漂浮条件F浮=G,即ρ水gV排=ρ蜡gV蜡得出ρ蜡=ρ水。
(2)测液体的密度
[方法一]
原理:F浮=G-F拉和F浮=ρ液gV排。(称重法)
器材:弹簧测力计、烧杯、适量的水、适量的待测液体和一个密度大于水和液体的物体。
过程:用上述器材分别测出物体在水中和待测液体中的浮力,则有
即:ρ液=。
[方法二]
原理:F浮=G物(漂浮法)
器材:量筒、水和待测液体、一个密度比水和待测液体小的物体。
过程:用上述器材分别测出物体在水中和待测液体中的V排即可,即:由G物=F浮水和G物=F浮液可知ρ水gV排水=ρ液gV排液,也即ρ液=。
考点一、液面高度变化的问题
典例1:(2022八上·镇海期末)如图所示,一块冰放在盛有的水的容器中,已知冰块与容器底部相接触并相互间有压力,则当冰完全融化成水后,容器中水面的位置将 。
【答案】上升
【解析】水面上升还是下降,取决于冰块排开水的体积与熔化成水后体积的大小关系,据此分析解答。
【解答】冰熔化前,它受到竖直向上的浮力和支持力,以及竖直向下的重力,
根据二力平衡的知识得到:F浮+F支=G冰,
所以F浮=ρ水V排g<G冰, ①
冰化水后质量不变,
根据G=mg可知,重力不变,即G冰=G水,
即:ρ冰V冰g=ρ水V水g ②
由①②可得:
ρ水V排g<ρ水V水g,
即:冰熔化为水的体积大于排开水的体积,
所以冰熔化后,水面将上升。
变式1:(2023八上·杭州期末)小金发现一冰块内有小石块,测得总质量是200g,放在水槽中,恰好悬浮在水中,则冰块与小石块的总体积是 cm3。当冰熔化后小石块沉入了水槽底,此时水槽中的水面 (选填“上升”、“下降”或“不变”)。(ρ水=1×103kg/m3,ρ冰=0.9×103kg/m3)
【答案】200;下降
【解析】(1)根据悬浮条件确定冰块的平均速度,再根据计算二者的总体积;
(2)将冰块熔化前二者排开水的总体积与熔化后水和石块的总体积进行比较即可。
【解答】(1)冰块和石块在水中悬浮,则它们的平均密度等于水的密度;
那么二者的总体积为:;
(2)冰块熔化前,二者在水中悬浮,则它们受到的浮力等于总重力;
冰块熔化后,此时冰块变成的水可以看似在水中悬浮,因此冰块受到的浮力不变;
而石块在水中下沉,那么它受到的浮力小于石块重力;
即冰块和石块受到的浮力小于它们的总重力;比较可知,它们受到的浮力减小了;
根据阿基米德原理F浮=ρ液gV排可知,它们排开水的总体积减小了,
那么水槽中的水面下降。
变式2:(2022八上·余姚期末)如图所示,在一个足够深的水槽中漂浮着一个木杯,此时杯口到水面的垂直距离为h,水槽底部到水面的垂直距离为H,若从水槽中取少量水倒入木杯中,则h (填“变大”,“变小”或“不变”,下同),H 。
【答案】变小;不变
【解析】(1)根据浮沉条件比较浮力的大小变化,再根据阿基米德原理F浮力=ρ液gV排分析水杯排开水的体积变化,根据V=Sh分析浸入深度的变化,从而确定露出水面高度的变化。
(2)水面高度的变化取决于水和杯子排开水的总体积的变化。
【解答】(1)水杯始终在水面漂浮,则它受到的浮力始终等于自身重力。从水槽中取少量的水倒入杯子中后,杯子的重力增大,则它受到的浮力增大。根据据阿基米德原理F浮力=ρ液gV排可知,杯子排开水的体积增大。根据V=Sh可知,杯子浸入水中的深度变大,而露出水面的高度h减小。
(2)原来杯子在水面漂浮,它受到的浮力等于重力,
则水和杯子排开水的总体积为:V总=V水+V排=V水+;
从水槽中取出少量水倒入杯子中后,杯子和水受到的浮力等于它们的总重力,
此时水和杯子排开水的总体积为:V总'=V水-V取出+=V水-V取出++;
而V取出=; 因此V总=V总';
即水和杯子排开水的总体积保持不变; 因此水面高度H保持不变。
变式3:(2022·浙江台州·八年级期末)小金把家里景观水池底部的鹅卵石取出清洗,他先将一个重为15N的空桶漂浮在水面上,然后将池底的鹅卵石捞出放置在桶内,桶仍漂浮在水面(不考虑捞出过程中带出的水,ρ水=1.0×103kg/m3)
(1)某块鹅卵石在水池底部时,它受到的浮力 它的重力(选填“大于”、“小于”或“等于”)。
(2)全部鹅卵石捞出放置在桶内时,水池内水面高度与鹅卵石未捞出时相比会_______(选填“上升”、“下降”或“不变”)。若此时桶排开水的体积为5.0×10-3m3,求桶内鹅卵石的总质量。
【答案】(1)小于
(2)上升;
F浮总=ρ液gV排=1×103Kg/m3×10N/kg×5.0×10-3m3=50N G石=F浮总-G桶=50N-15N=35N
【解析】(1)根据浮沉条件比较浮力和重力的大小
(2)水面上升还是下降,取决于鹅卵石排开水的体积大小,根据阿基米德原理F浮=ρ液gV排比较即可。
首先根据阿基米德原理F浮=ρ液gV排计算出桶和鹅卵石受到的总浮力,再根据G石=F浮总-G桶计算出鹅卵石的重力,最后根据计算出鹅卵石的质量。
【解答】(1)鹅卵石在池水里处于下沉状态,则它受到的浮力小于重力。
(2)鹅卵石在桶内处于漂浮状态,则此时它受到的浮力大于沉在池底时的浮力。根据阿基米德原理F浮=ρ液gV排可知,则此时它排开水的体积大于沉在池底时的体积,因此水池内水面高度与未捞出时相比会上升。
和鹅卵石受到的总浮力F浮总=ρ液gV排=1×103kg/m3×10N/kg×5.0×10-3m3=50N;
鹅卵石的重力:G石=F浮总-G桶=50N-15N=35N ;
鹅卵石的质量:。
考点二、利用浮力测物体密度
典例1:(2022八上·宁海期中)小明用装有适量水的薄壁小试管、螺母和细线制成一个测量小石块密度的装置。将此装置放入水中静止时,试管署出水面的高度h1为5cm,如图甲所示:在试管中轻轻放入小石块,装夏在水中静止时,试管露出水面的高度h2为2cm,如图乙所示。已知小石块放入试管前后.试管中的液面差h3为2cm。则
(1)小试管所受浮力的方向为
(2)石块的密度为 kg/m3
【答案】(1)竖直向上
(2)3×103
【解析】(1)浮力的方向为竖直向上;
(2)比较甲、乙两图可知,试管两次受到的浮力之差就是小石块的重力;进一步求出小石块的质量;
根据小石块放入试管前后,试管中的液面差h3为2cm可以求出小石块的体积;最后利用密度公式求出小石块的密度。
【解答】(1)小试管所受浮力的方向为竖直向上;
(2)比较甲、乙两图可知,两次受到的浮力之差就是小石块的重力,
即石块的重力G=ΔF浮=ρ水g(h1-h2)S容=ρ水g×(0.05m-0.02m)S容=ρ水gS容×0.03m,
小石块放入试管前后,试管中的液面差h3为2cm,
所以小石块的体积为V=(h1-h2-h3)S容=(0.05m-0.02m-0.02m)S容=0.01m×S容,
则小石块的密度。
变式1:下面是小金利用量筒和水测量橡皮泥密度的实验操作情景,
(1)乙图中橡皮泥受到的浮力为______牛。
(2)由图中读数可算出橡皮泥的密度是______kg/m3。
【答案】0.14 1.75×103
【解析】解:(1)[1]橡皮泥浸没之前水面对应的示数为V1=50mL=50cm3
橡皮泥漂浮在水面上水面对应的示数为V2=64mL=64cm3
乙图中橡皮泥排开液体的体积V'=V2-V1=64mL-50mL=14mL=14cm3=1.4×10-5m3
乙图中橡皮泥受到的浮力为F浮=ρ水gV排=1.0×103kg/m3×10N/kg×1.4×10-5m3=0.14N
(2)[2]橡皮泥团成球浸没在水中,量筒中水面对应的示数为V3=58mL=58cm3
橡皮泥漂浮在水面上,受到的重力等于排开水的重力,所以橡皮泥的质量等于排开水的质量,所以
m=m排水=(V2-V1)ρ水
橡皮泥的体积为V=V3-V1
所以橡皮泥的密度
变式2:(2023八上·椒江期末)小科在验证阿基米德原理时,利用溢水杯、弹簧测力计、铁块、小桶、细线等进行实验,具体操作步骤如图:
(1)细心的同学发现图乙步骤中存在错误,请指出该错误是: 。如果不加改正,会导致浮力F浮 (选填“大于”、“等于”或“小于”)排开水的重力G排。
(2)纠正错误后,若图中测得的F1、F2、F3、F4关系满足 ,则阿基米德原理得到验证。
(3)实验后,小科发现利用实验所得数据还能测出所用铁块的密度,ρ铁= (水的密度用ρ水表示)。
【答案】(1)溢水杯中没有装满水;大于
(2)F2﹣F3=F4﹣F1
(3) ρ水
【解析】(1)根据图乙可知,当溢水杯中装满水时,物体排开水的重力才会恰好等于它受到的浮力。如果没有装满水,那么放入物体后水面先上升到溢水杯口才会有水排出,而不是马上排出水,据此比较浮力和排开水的重力大小。
(2)根据阿基米德原理F浮=G排分析解答;
(3)根据称量法计算出铁块受到浮力,根据阿基米德原理计算出铁块的体积,根据密度公式计算铁块的密度。
【解答】(1)根据图片可知,图乙中存在的错误:溢水杯中没有装满水。如果不加改正,会导致浮力F浮大于排开水的重力G排。
(2)根据图片可知,图乙中物体的重力G=F2,丙图中物体浸没时测力计的示数为F3,
则物体受到的浮力:F浮=G-F拉=F2-F3;
空桶的重力G桶=F1,桶和排出水的总重力G总=F4;
则物体排开水的重力G排=G总-G桶=F4-F1;
根据阿基米德原理F浮=G排得到:F2-F3=F4-F1。
(3)综上所述,铁块的体积:;
则铁块的密度:。
变式3:(2023八上·鄞州期末)气体的密度与压强有关。为测量实验室内空气的密度,小明在实验室按如图所示步骤进行实验:
①如图甲,将一打足气的足球,放入装满水的容器中,测得溢出水的体积为426毫升。
②如图乙,将500毫升装满水的量筒倒置于水槽中,用气针和乳胶管将足球中的气体慢慢排入该量筒,同时调整量筒的位置,当量筒内外水面都与500毫升刻度线相平时,停止排气。共排气10次。
③如图丙,拔除气针和乳胶管,把排气后的足球放入装满水的容器中,测得溢出水的体积为420毫升。
(1)图乙中,当量筒内外水面都与500毫升刻度线相平时停止排气,其目的是 。
(2)图丙中,足球受到的浮力?
(3)根据测得的数据,计算实验室中空气的密度?
【答案】(1)使量筒内的气压等于外界气压
(2)根据丙图可知,
足球受到的浮力为:F浮=ρ液gV排=103kg/m3×10N/kg×420×10-6m3=4.2N;
(3)甲图中足球受到的浮力:F浮'=ρ液gV排'=103kg/m3×10N/kg×426×10-6m3=4.26N;
则足球的重力为:G=F浮'-F浮=4.26N-4.2N=0.06N;
足球内气体的体积:V=500mL×10=5000mL=5×10-3m3;
则气体的密度:。
【解析】(1)当量筒内外水面相平时,量筒内的气压等于外界大气压强,此时测出气体的体积就是正常情况的体积。
(2)根据阿基米德原理F浮=ρ液gV排计算丙图中足球受到的浮力;
(3)甲和丙中足球受到的浮力之差等于其中气体的重力,而气体的体积等于量筒内排气之和,最后根据密度公式计算气体的密度即可。
【解答】(1)图乙中,当量筒内外水面都与500毫升刻度线相平时停止排气,其目的是:使量筒内的气压等于外界气压。
4.[2021·丽水] 归纳与演绎是科学学习中非常重要的科学方法,下表是兴趣小组归纳“根据ρ=,运用浮力知识间接测量固体密度”的方法,请完成表格。
方法 实验器材 操作过程 思维过程 数据处理 适用范围
一 弹簧测力计、烧杯、水 m=,V物=V排=,ρ物=== ρ物= kg/m3 ρ物>ρ液
二 量筒、细铁丝、水 ……ρ物= ( 用V1、V2、V3、ρ水表示) …… ρ物<ρ液
5.张超同学利用量筒和水测量橡皮泥的密度,请根据图完成下列填空。
(1)在量筒中装适量的水,读出水面对应的刻度值V1= 。
(2)把橡皮泥捏成碗状,小心放入量筒使之漂浮在水面上,读出此时水面对应的刻度值V2,根据漂浮原理可求出橡皮泥的质量m= 。(g取10 N/kg)
(3)再把橡皮泥团成球放入量筒使之沉入水底,读出此时水面对应的刻度值V3。
(4)利用密度计算公式可推导出橡皮泥密度的表达式为ρ= 。由图中读数可算出橡皮泥的密度是 kg/m3。
6.小晨设计了一个用排水法测某实心金属块的密度的实验。实验器材有小空桶、溢水杯、烧杯、量筒和水。实验步骤如下:
①让小空桶漂浮在盛满水的溢水杯中,如图 甲所示;
②将金属块浸没在水中,测得溢出水的体积为20 mL,如图乙所示;
③将烧杯中 20 mL水倒掉,从水中取出金属块,如图丙所示;
④将金属块放入小空桶,小空桶仍漂浮在水面上,测得此时溢出水的体积为 44 mL,如图丁所示。
请回答下列问题:
(1)被测金属块的密度是 g/cm3。(g取10 N/kg)
(2)在实验步骤③和④中,将沾有水的金属块放入小空桶,测出的金属块的密度将 (填“偏大”“不变”或“偏小”)。
4、1.3×103
(1)ρ===3×103 kg/m3;
(2)因为物体漂浮在水中,
所以G=F浮=G排=ρ水(V2-V1)g,
所以m物=m排=ρ水(V2-V1),
物体的体积:V物=V3-V1,
物体的密度:ρ物==。
5.(1)50 cm3 (2)14 g
(4) 1.75×103
6.(1)2.2 (2)不变
考点三、浮力与曲线变化
典例1:(2022八上·余姚期中)将一个底面积为 0.01 m2的长方体木块用细线拴在一个空容器的底部,然后向容器中缓慢加水直到木块上表面与液面相平,如图甲所示。在整个过程中,木块底部受到水的压强随容器中水的深度的变化如图乙所示,则木块所受到的最大浮力为 N,木块重力为 N,细线对木块的最大拉力为 N。
【答案】15;9;6
【解析】(1)由图乙可知,木块恰好漂浮时木块底部受到水的压强,根据求出木块底部受到水向上的压力,根据浮力产生的原因F浮=F向上-F向下求出木块受到的浮力,根据漂浮条件求出木块的重力;
(2)木块浸没时排开水的体积最大,受到的浮力最大,细线对木块的拉力最大,根据图乙读出此时木块底部受到水的压强,根据求出木块底部受到水向上的压力,根据浮力产生的原因F浮=F向上-F向下求出木块受到的最大浮力;
(3)根据二力平衡的知识可知,细线对木块的最大拉力等于最大浮力减去自身的重力。
【解答】(1)由图乙可知,在9cm~16cm内,木块处于漂浮状态,此时木块底部受到水的压强p=900Pa,
由可得,木块底部受到水向上的压力:F向上=p向上S=900Pa×0.01m2=9N,
由浮力产生的原因F浮=F向上-F向下可得,木块受到的浮力:F浮=F向上-F向下=F向上=9N,
因物体漂浮时受到的浮力和自身的重力相等,
所以,木块的重力:G木=F浮=9N;
(2)木块浸没时排开水的体积最大,受到的浮力最大,细线对木块的拉力最大,此时木块下表面所处的深度最大,受到水的压强最大,
由图乙可知,木块上表面与液面相平时,木块底部受到水的压强p′=1500Pa,
此时木块底部受到水向上的压力:F向上′=p向上′S=1500Pa×0.01m2=15N,
木块受到的最大浮力:F浮大=F向上′-F向下=F向上′=15N,
(3)由力的平衡条件可得,细线对木块的最大拉力:F拉大=F浮大-G木=15N-9N=6N。
变式1:(2022八上·鄞州期中)如图甲所示,一个棱长为10cm、重为9N的正方体物块M,水平放置在一个方形容器中,M与容器底部不密合。以恒定水流向容器内注水,容器中水M的深度h随时间t的变化关系如图乙所示,当t=100s时,物块M在水中处于 (选填“沉底”、“悬浮”或“漂浮”)状态,图乙中a的值为 cm。
【答案】漂浮;9
【解析】(1)已知正方体物块M的棱长,由正方体的体积公式可求物块的体积,已知物块的重力可求物块的质量,根据公式可求物块的密度,再与水的密度进行比较,根据物块M的密度小于水的密度,判断物块M最终会漂浮,然后根据图像分析出物块M恰好漂浮的时间点为t=40s,进而判断出t=100s时物块M在水中的状态;
(2)根据物体漂浮条件求出物块M受到的浮力,根据阿基米德原理求出此时物块M排开水的体积,再由V排=SMh浸可求出此时物块浸入水中的深度,即为此时水的深度a的值。
【解答】(1)正方体物块M的体积:V=L3=(10cm)3=1000cm3=0.001m3;
物块M的质量:;
物块M的密度:;
即物块的密度小于水的密度,物块在水中最终会漂浮,
由图象可知,0~40s过程中,随着水的深度逐渐增加,物块M排开水的体积也变大,则物块M所受到水的浮力也变大,
当t=40s时,水的深度变化变慢,说明此时物块M刚好处于漂浮状态,因此当t=100s时,物块M在水中处于漂浮状态;
(2)当t=40s时,物块M刚好处于漂浮状态,则F浮=GM=9N,
根据F浮=ρ水gV排可得此时物块M排开水的体积:,
由V排=SMh浸可得,此时水的深度:。
变式2:(2020八上·奉化期末)如图甲所示,在容器底部固定一轻质弹簧,弹簧受到的拉力跟弹簧的伸长量关系如图乙所示,弹簧上端连有一边长为0.1m的正方体物块A,当容器中水的深度为20cm时,物块A有2/5的体积露出水面,此时弹簧恰好处于自然伸长状态。求:
(1)物块A的密度。
(2)往容器缓慢加水(水未溢出)至物块A恰好浸没时,弹簧的伸长量为多少 再继续加水,木块受到浮力怎么变化
【答案】(1)弹簧恰好处于自然状态时没有发生形变,弹簧对物体没有拉力,物体只受重力和浮力作用,
故F浮=G,即ρ水gV排=ρ物gV,所以ρ物= ρ水= ×1×103kg/m3=0.6×103kg/m3
(2)物块A刚好完全浸没水中时,F浮=ρ水gV=1×103kg/m3×10N/kg×10-3m3=10N
G=mg=ρ物gv=0.6×103kg/m3×10N/kg×10-3m3=6N
弹簧受到的拉力F1=F浮-G=10N-6N=4N
由图乙可知:此时弹簧伸长了4cm
因木块浸没在水中,排开液体体积不变,故浮力不变
【解析】(1)弹簧处于自然伸长状态时,物块不受弹力,那么此时物块受到的浮力等于自身的重力,即F浮=G,用阿基米德原理和密度公式将等式拆开,代入数据计算即可;
(2)当物块A完全浸没时,它受到平衡力,即F浮=G+F弹力;首先根据 F浮=ρ水gV 计算出浮力,再根据 G=mg=ρ物gV计算出它的重力,最后根据前面的关系计算出弹簧的弹力,并根据乙图计算弹簧伸长的长度。
变式3:(2022八上·平阳月考)如图甲所示,一个边长是10cm的立方体木块,下面用一段细线与木块相连,细线另一端固定在容器底(容器高比细线与木块边长之和大得多)。现向容器中慢慢加水,直到细线拉直,如图乙所示。若细线的拉力用F表示,倒入容器中水的深度用h表示(g= 10 N/kg)。
(1)图丙中的A点对应木块在水中的位置是处于 状态。
(2)该木块浸没在水中所受的浮力为多少牛顿?
(3)该木块的密度为多少?
(4)请在丁图中作此过程中木块所受浮力F浮随水的深度h变化的大致图象。
【答案】(1)漂浮
(2)木块的体积:V=10cm×10cm×10cm=1000cm3=1×10-3m3;
木块完全浸没在水中,则V排=V=1×10-3m3;
木块浸没在水中所受的浮力:F浮=ρgV排=1.0×103kg/m3×10N/kg×1×10-3m3=10N;
(3)由题意可知,线拉直后,水还在倒入,所以木块排开水的体积继续增大,浮力增大,则下端线的拉力也相应增大;当木块浸没后,木块排开水的体积不变,浮力不变,则下端线的拉力也不变。
由图象可知,木块浸没时所受拉力最大为4牛,
由力的平衡条件可得F浮=G+F,
所以木块的重力:G=F浮-F=10N-4N=6N,
则木块的质量:
木块的密度:。
(4)
【解析】(1)对物体进行受力分析,当物体不受绳子拉力作用时,物体只受重力和浮力的作用;
(2)已知立方体木块的边长可求得其体积,该木块完全浸没在水中时,V排=V,根据F浮=ρgV排可求出木块浸没在水中的浮力;
(3)由图丙可知浸没时绳子的拉力,根据平衡条件求出木块的重力,根据G=mg求出木块的质量,再利用可求出木块的密度;
(4)分析物体从液面逐渐浸入直到浸没的过程中、木块排开水的体积变化,再根据阿基米德原理F浮=ρ液gV排分析浮力的大小变化。
【解答】(1)根据图丙中的A点对应木块在水中的位置可知,物体只受重力和浮力的作用,绳子对物体的拉力为零,并且物体处于静止状态时,部分体积露出水面,因此此时处于漂浮状态;
(4)①在木块漂浮之前,随着水的深度增大,它排开水的体积增大,根据阿基米德原理F浮=ρ液gV排可知,它受到的浮力逐渐增大;
②当浮力与重力相等时,木块处于漂浮状态。随着水位的升高,木块的位置不断升高,但是浮力保持不变,应该为6N;
③当细线拉直后,木块的位置不能升高,则它排开水的体积继续增大。根据阿基米德原理F浮=ρ液gV排可知,它受到的浮力逐渐增大;
④当木块完全浸没后,它排开水的体积达到最大,此时浮力达到最大为10N。随着水位的升高,它受到的浮力保持不变。如下图所示:
考点四、浮力的受力分析计算
典例1:(2023八上·海曙期末)如图,体积相同的两物体A、B用不可伸长的细线系住,放入水中后,A有四分之一体积露出水面,细线被拉直。已知A重4N,B受到的浮力为8N,A、B密度之比为2:5。那么下列说法正确的是( )
A.A,B所受的重力之比为5:2 B.A、B所受的浮力之比为1:4
C.细线对A的拉力大小为1N D.B对容器底部的压力为零
【答案】D
【解析】(1)由题知,A、B密度之比ρA:ρB=2:5,VA:VB=1:1,利用G=mg=ρVg求A、B所受的重力之比;
(2)A、B的体积相同,都为V,A有四分之一体积露出水面,则A排开水的体积V排A=V,B排开水的体积V排B=V,利用阿基米德原理求A、B所受的浮力之比;
(3)知道B受到的浮力,根据A、B所受的浮力之比可求A受到的浮力,细线对A的拉力大小等于A受到的浮力减去A的重力;
(4)上面求出了A、B的重力之比,知道A的重力,可求B的重力;对B受力分析,求出B对容器底部的压力。
【解答】A.由题知,A、B密度之比ρA:ρB=2:5,VA:VB=1:1,
由G=mg=ρVg可得,A、B所受的重力之比:GA:GB=ρAVAg:ρBVBg=ρA:ρB=2:5,故A错误;
B.已知A、B的体积相同,设均为V,A有四分之一体积露出水面,
则A排开水的体积V排A=V,B排开水的体积V排B=V,
则A、B所受的浮力之比:F浮A:F浮B=ρ水V排Ag:ρ水V排Bg=V:V=3:4,故B错误;
C.由题知,B受到的浮力F浮B=8N,
因F浮A:F浮B=3:4,则A受到的浮力:F浮A=F浮B=×8N=6N,
A受到向上的浮力、向下的重力和拉力,
由力的平衡条件可得细线对A的拉力大小:F拉=F浮A-GA=6N-4N=2N,故C错误;
D.因为GA:GB=2:5,且GA=4N,所以GB=GA=×4N=10N,
B对容器底部的压力:F压=F浮B+F拉-GB=8N+2N-10N=0N,故D正确。
变式1:(2022八上·平阳月考)物体浮在甲液面时有1/5的体积露出液面,物体浮在乙液面时有1/3的体积露出液面,则甲、乙两液体的密度之比是( )
A.5 :12 B.4 :15 C.5 :6 D.12 :5
【答案】C
【解析】根据漂浮条件和阿基米德原理F浮=ρ液gV排分析判断。
【解答】物体在液面漂浮,则它受到的浮力始终等于重力,即浮力相等;
那么:F浮=F浮';
ρ甲gV排甲=ρ乙gV排乙;
ρ甲V排甲=ρ乙V排乙;
那么:.
故选C。
变式2:如图用细线将正方体A和物体B相连放入水中,两物体静止后恰好悬浮,此时A上表面到水面的高度差为0.12m。已知A的体积为1.0×10﹣3m3,所受重力为8N;B的体积为0.5×10﹣3m3,g取10N/kg,求:
(1)A的密度;
(2)细线对B的拉力大小。
【答案】(1)解: mA=GA/g=8N/10N/kg=0.8kg
ρA=mA/VA=0.8kg/1.0×10﹣3m3=0.8×103kg/m3
答:A的密度为0.8×103kg/m3
(2)A受到浮力F浮=ρgV排=1×103kg/m3×10N/kg×1.0×10﹣3m3=10N;因A恰好悬浮所以F浮=GA+F拉A
细线对A的拉力F拉A=F浮﹣GA=10N﹣8N=2N
因为物体间力的作用是相互.的,所以细线对B的拉力F拉B=F拉A=2N。答:细线对B的拉力2N
【解析】(1)首先根据计算物体A的质量,然后再根据计算物体A的密度;
(2)首先根据阿基米德原理计算出A浸没时受到的浮力,然后根据物体A的受力情况:计算细绳对A的拉力,最后根据相互作用力的规律求出细线对B的拉力。
变式3:如图所示,在一个装满水的容器中,轻质弹簧的一端连着小球,另一端固定在容器底部。已知小球的体积是500cm3,小球静止时受到弹簧对它的作用力为4N。则:
(1)此时小球受到的浮力为多少?
(2)如果剪断弹簧后,请分析小球的运动情况,并计算再次静止后小球受到的浮力是多少?
【答案】(1)∵小球完全浸没在水中 ∴V排=V物=500cm3=0.0005m3
F浮=ρ液g V排=1.0×103kg/m3×10N/kg×0.0005m3=5N
(2)解:小球静止时对其进行受力分析可分为二种情况如图所示
由图1可知,G=F浮+F弹=5N+4N=9N
剪断弹簧后,G>F浮 , 小球下沉至容器底部静止,此时F浮=5N
由图2可知,G=F浮-F弹=5N-4N=1N
剪断弹簧后,G<F浮,小球上浮至水面处于飘浮状态,此时F浮=G=1N
【解析】(1)物体浸没时, V排=V物,利用阿基米德原理公式 F浮=ρ液g V排求出 此时小球受到的浮力;(2) 小球静止时对其进行受力分析可分为二种情况:一种情况是 小球下沉至容器底部静止,求出浮力;另一种情况是小球上浮至水面处于飘浮状态。
1.如图,一杯果汁(密度大于水),加冰后液面正好同杯口相平。则在冰块熔化过程中( )
A.液面不变,液体不溢出 B.液面不变,液体溢出 C.液面下降 D.无法确定
【答案】B
【解析】将冰块排开果汁的体积和熔化成水的体积进行比较,如果后者大,那么液体溢出;如果前者大,那么液体不溢出。
冰块在液面上漂浮,那么它受到的浮力等于重力,
即F浮力=G; 那么它排开果汁的体积:;
冰块熔化后质量不变, 那么熔化成水的体积:;
因为ρ水<ρ果汁 , 所以V水>V果汁。
因此液面不变,但是液体溢出。
2.如图所示,容器内有水,有一试管下面挂一小铁块,浮在水面上。现将小铁块取下放入试管中,试管仍浮在水面,则( )
A.液面上升 B.试管底部受到液体的压强变大
C.液面下降 D.试管所受到的浮力不变
【答案】B
【解析】(1)液面上升还是下降,取决于排开水的体积。根据二力平衡的知识比较前后两种状态下受到的总浮力的变化,再根据阿基米德原理F浮=ρ液gV排比较V排的变化,最终确定液面的变化情况;
(2)分析前后两种情况下试管受到浮力的变化,再根据阿基米德原理F浮=ρ液gV排比较试管排开水的体积变化,进而得到试管底部的深度变化,最后根据液体压强公式p=ρ液gh确定试管底部受到压强的变化。
【解答】无论小铁块在试管外,还是在试管内,试管和铁块构成的整体都在水面漂浮,那么它们受到的浮力都等于自身的重力之和。因为它们的重力之和不变,所以受到的浮力不变。根据阿基米德原理F浮=ρ液gV排可知,前后两种情况下排开水的总体积保持不变,自然水面不会发生改变,故A、C错误;
当小铁块在试管外时,铁块也会受到浮力,因此它受到的浮力肯定小于它们受到的总浮力。当小铁块在试管内时,铁块不会受到浮力,因此试管受到的浮力等于它们受到的总浮力。前后比较可知,试管受到的浮力增大了,故D错误;
试管受到的浮力增大,根据阿基米德原理F浮=ρ液gV排可知,试管排开水的体积增大,因此试管底部的深度增大了。根据公式p=ρ液gh可知,试管底部受到液体的压强变大了,故B正确。
3.(2023八上·杭州期末)把一个木球轻轻放入盛满水的溢杯中(足够大),溢出100g水;若将此木球从水中取出,擦干后轻轻放入盛满酒精的溢杯中(足够大),则溢出酒精的质量是(ρ木=0.6×103kg/m3,ρ酒精=0.8×103kg/m3,ρ水=1×103kg/m3)( )
A.大于100g B.等于100g C.小于100g D.无法确定
【答案】B
【解析】将木球的密度与水和酒精的密度进行比较,根据浮沉条件计算它受到的浮力,进而计算出它排开酒精的质量。
【解答】因为木球的密度小于水的密度,所以木球在水中漂浮,那么它受到的浮力等于重力。
因为木球的密度小于酒精的密度,所以木球在酒精中漂浮,那么它受到的浮力等于重力。
比较可知,木球在水中受到的浮力等于在酒精中受到的浮力;
即F浮水=F浮酒;
G排水=G排酒;
m排水g=m排酒;
那么m排酒=m排水=100g。
故选B。
4.(2022八上·杭州期中)将一个物块轻轻放入盛满水的烧杯中,静止后有81克水从烧杯中溢出;将其轻轻放入盛满酒精的烧杯中,静止后有72克酒精从烧杯中溢出。已知酒精密度:0.8×103kg/m3,则该物块在水中的状态及物块的密度分别为( )
A.悬浮 1.0×103kg/m3 B.漂浮 0.9×103kg/m3
C.漂浮 0.92×103kg/m3 D.下沉 1.2×103kg/m3
【答案】B
【解析】分三种情况(大于等于水的密度、大于酒精的密度小于水的密度、小于等于酒精的密度)分析,得出物体的密度大于酒精的密度、小于水的密度,从而确定物体在水中漂浮,根据漂浮条件求出物体重,再根据在酒精中受到的浮力求出物体的体积,利用密度公式求物体的密度。【解答】①假设ρ物≥ρ水,物体将在水中悬浮或下沉在杯底,在酒精中下沉在杯底,此时排开水或酒精的体积相同,根据F浮=ρ液V排g可知受到的浮力关系为5:4,
根据F浮=G排=G溢=m溢g可知浮力关系为9:8,所以ρ物≥ρ水不可行;
②假设ρ物≤ρ酒精,物体将在水中漂浮,在酒精中漂浮或悬浮,这样受到的浮力相等,都等于自重,但是实际受到的浮力不相等,所以ρ物≤ρ酒精不可行;
可见物体的密度一定是大于酒精的密度、小于水的密度,所以物体在水中会漂浮,而在酒精中下沉到杯底:
③因为物体在水中漂浮,漂浮时物体所受浮力等于自身重力,即F浮=G物=m物g,
根据阿基米德原理可知F浮=G排=G溢=m溢g,
所以m物=m溢=81g,
因为物体在酒精中下沉,ρ酒精=0.8×103kg/m3=0.8g/cm3,
所以,
则物体的密度:。
故选B。
5.(2023八上·宁海期末)水平桌面上两个相同的烧杯中分别装有甲、乙两种不同液体,将两个用不同材料制成的正方体A、B(VA<VB),按如图两种方式放入两种液体中,待静止后B刚好浸没在甲液体中,两杯中液面恰好相平。下列说法正确的是( )
A.甲液体的密度大于乙液体的密度
B.甲液体对杯底的压强等于乙液体对杯底的压强
C.甲液体对B下表面的压强等于乙液体对A下表面的压强
D.装甲液体的烧杯对水平桌面的压力小于装乙液体的烧杯对水平桌面的压力
【答案】D
【解析】(1)把A、B两物体作为一个整体,该整体在两液体中都处于漂浮状态,根据漂浮条件可知所受浮力的大小关系;结合题意和图示判断V排的关系,根据F浮=ρ液gV排可比较两种液体的密度关系;
(2)知道两种液体的密度关系,且两杯中液面恰好相平,根据p=ρ液gh分析液体对杯底的压强关系;
(3)根据漂浮条件、浮力产生的原因以及分析液体对物体下表面的压强关系;
(4)先比较两种液体的体积关系和重力关系,再根据”烧杯对水平桌面的压力等于烧杯、物体和液体的总重力“进行分析。
【解答】A、把A、B两物体作为一个整体,由图知,该整体在两液体中都处于漂浮状态,
由漂浮条件可知F浮=GA+GB,所以该整体在两液体中受到的浮力相等;
由图知V排甲=VB,V排乙=VA,且VA<VB,所以V排甲>V排乙;
因整体在两液体中受到的浮力相等,且排开甲液体的体积较大,
由F浮=ρ液gV排可知,两液体的密度关系:ρ甲<ρ乙,故A错误;
B.由题意可知两液体的深度h相同,且ρ甲<ρ乙,由p=ρ液gh可知,甲液体对杯底的压强小于乙液体对杯底的压强,
故B错误;
C.因整体受到的浮力相等(即甲液体中B物体受到的浮力等于乙液体中A物体受到的浮力),且两物体上表面没有受到液体的压力,
所以由浮力产生的原因F浮=F向上-F向下可知,甲液体中B物体与乙液体中A物体的下表面受到的液体压力相等,
由图知B的底面积更大,由可知,甲液体对B下表面的压强小于乙液体对A下表面的压强,故C错误;
D.两烧杯中液面恰好相平且烧杯相同,则液体与物块排开液体的体积之和相同,但V排甲>V排乙,所以甲液体的体积较小。
又知ρ甲<ρ乙,则根据G液=m液g=ρ液gV液可知,甲液体的重力较小;
烧杯对水平桌面的压力F=G杯+GA+GB+G液,因两烧杯相同、其重力相同,且A、B两物体的重力不变,甲液体的重力较小,
所以装甲液体的烧杯对水平桌面的压力较小,
故D正确。
6.(2023八上·宁海期末)迪迪同学将质量为120g的物体放入盛满水的溢水杯中,当物体静止时,溢水杯中溢出了100cm3的水,物体受到的浮力为 N,则此时物体在水中 (选填“漂浮”、“悬浮”或“沉底”).
【答案】1;沉底
【解析】首先根据阿基米德原理F浮=ρ液gV排计算物体受到的浮力,再与重力比较,根据浮沉条件判断物体在水中的状态。
【解答】根据题意可知,
物体在水中受到的浮力:F浮=ρ液gV排=103kg/m3×10N/kg×100×10-6m3=1N;
物体的重力G=mg=0.12kg×10N/kg=1.2N;
即浮力小于重力,
那么物体在水中沉底。
7.(2022八上·富阳期中)小科按照教材中"综合实践活动"的要求制作简易密度计。
(1)取一根粗细均匀的饮料吸管,在其下端塞入适量金属丝并用石蜡封口。塞入金属丝的目的是使吸管能漂浮在液体中。这根吸管竖直漂浮在不同液体中时,液体密度越大,它露出液面部分的长度 (选填“越长”、“越短”或“”不变”)
(2)小科根据图甲在吸管上标出1.0刻度线(单位g/cm , 下同),再利用上述关系式进行计算,标出了0.9、1.0、1.1的刻度线,如图乙A,B,C,D所示,则标示正确的图是
(3)将吸管放到水中的情境如丙图(a)所示,测得浸入的长度为H;放到另一液体中的情景如丙图(b)所示,浸入的长度为h。用ρ液、ρ水分别表示液体和水的密度,则h和ρ水、ρ液,H的关系式是h= 。
【答案】(1)越长
(2)C
(3)
【解析】(1)根据浮沉条件和阿基米德原理F浮=ρ液gV排分析即可;
(2)根据阿基米德原理F浮=ρ液gV排分析吸管上刻度随液体密度的变化规律即可;
(3)根据浮沉条件和阿基米德原理F浮=ρ液gV排推导计算即可。
【解答】(1)密度计始终漂浮在液面上,则它受到的浮力始终等于重力,即浮力保持不变。
根据阿基米德原理F浮=ρ液gV排可知,当液体密度增大时,密度计排开液体的体积减小;
根据V露=V-V排可知,它露出液面的部分长度越大。
(2)根据阿基米德原理F浮=ρ液gV排=ρ液gSh排可知,液面的密度与密度计浸入的深度成反比,即液体密度越大,浸入深度越小,而此时刻度越靠下,那么从上到下,密度计上的刻度值越来越大,且越往下刻度越密集,故选C。
(3)根据丙图可知,密度计受到的浮力相等;
即Fa=Fb;
ρ水gV排=ρ液gV排;
ρ水gSH=ρ液gSh;
ρ水H=ρ液h;
解得:。
8.(2023八上·义乌期末)小明利用电子秤、长方体铁块、细线、圆柱形玻璃板、糖水,探究“影响浮力大小的因素”实验。
(1)如图甲,将搅拌均匀的糖水装入柱形杯中,置于电子秤上,示数为400.0g。用质量和体积均不计的细线系好铁块,缓慢浸入装有糖水的容器中,直到乙图所示的位置,发现该过程中电子秤示数逐渐增大。说明:铁块所受浮力大小与
有关;
(2)继续将铁块缓慢浸没到图丙所示位置,通过观察与比较,小明认为物体所受浮力大小与浸没后的深度
(选填“有关”或“无关”);
(3)将铁块沉入杯底,松开细线(细线已松弛),此时电子秤的示数如图丁所示,糖水密度为
kg/m3;(铁的密度是7.9克/厘米3)
(4)放置一段时间后,将铁块从糖水中慢慢提起。小明发现铁块离开杯底至上表面露出液面前,电子秤示数逐渐减小,造成这种现象的主要原因可能是
。
【答案】(1)排开液体的体积
(2)无关
(3)1.12×103
(4)放置一段时间后糖水密度不均匀
【解析】(1)电子秤的示数增大,说明铁块受到的浮力增大,分析缓慢入水过程中影响浮力的哪个因素发生改变即可。
(2)当深度增大时,如果电子秤的示数发生改变,那么说明浮力大小与浸没深度有关;否则,二者无关。
(3)甲和丁的示数之差等于铁块的质量,根据公式计算铁块的体积,也就是铁块排开糖水的体积,最后根据计算糖水密度即可。
(4)电子秤的示数逐渐减小,说明铁块受到的浮力逐渐减小,而它排开糖水的体积不变,根据阿基米德原理F浮=ρ液gV排可知,肯定是糖水的密度发生了变化,据此分析解答。
【解答】(1)在铁块缓慢浸入糖水中时,它排开糖水的体积不断增大,而电子秤的示数增大说明它受到的浮力增大,那么得到结论:铁块所受浮力大小与排开液体的体积有关。
(2)继续将铁块缓慢浸没到图丙所示位置,它浸没的深度不断增大,但是电子秤的示数保持不变,说明它受到的浮力不变,那么得到结论:物体所受浮力大小与浸没后的深度无关。
(3)根据甲、丁可知,铁块的质量为:m铁=558g-422.4g=135.6g;
则铁块的体积为:;
甲和乙的示数之差等于铁块排开糖水的质量:m排=422.4g-400g=22.4g;
则糖水的密度:。
(4)小明发现铁块离开杯底至上表面露出液面前,电子秤示数逐渐减小,造成这种现象的主要原因可能是:放置一段时间后糖水密度不均匀。
9.(2020八上·余杭月考)人们常用“冰山一角"来形容事物显露出来的仅仅是其很小的部分,更多的还隐藏在表面现象之下。事实上,冰山浮在海水中的确只露”一角"(如图所示)。若现有一座冰山,它露出海面的体积是2000m3 , (已知:海水的密度取ρ海水=1×103kg/m3 , 冰的密度ρ冰=0.9×103kg/m3)。则:
(1)假如此冰山完全熔化,则液面将________(填“不变”、“降低”或“上升");
(2)这座冰山的总体积为多少?
【答案】(1)不变
(2)冰山在海面漂浮,那么得到:
F浮=G;
ρ水gV排=ρ冰gV;
ρ水V排=ρ冰V;
103kg/m3×(V-2000m3)=0.9×103kg/m3×V;
解得:V=20000m3。
【解析】(1)冰熔化成水质量不变,根据密度公式计算出熔化成水的体积,根据阿基米德原理计算出冰山在海水中的V排 , 然后二者比较即可;
(2)首先根据漂浮条件列出浮力和重力的关系式,然后根据密度公式和阿基米德原理将公式拆开,代入数据计算出冰山的体积即可。
【解答】(1)冰山在海水表面漂浮,那么它受到的浮力等于重力,
它排开海水的体积:;
冰山熔化后,水的体积为:;
因为熔化前后,冰山的重力G不变,且海水的密度等于淡水密度,
所以V排=V;
因此冰山完全熔化受,液面会不变。
(2)冰山在海面漂浮,那么得到:
F浮=G;
ρ水gV排=ρ冰gV;
ρ水V排=ρ冰V;
103kg/m3×(V-2000m3)=0.9×103kg/m3×V;
解得:V=20000m3。
10.(2022八上·鹿城月考)小华发现用密度计测量液体密度需要大量液体,因此他用家里闲置的眼镜盒自制了密度计,该自制密度计高为16厘米,横截面积为20cm2,在盒子底部加入沙子使密度计能竖立水中,密度计自重200克。使用时烧杯中装有一定量的水。求:
(1)未放入待测液体之前,该密度计所受浮力多大
(2)往密度计中放入10毫升待测液,密度计浸入深度为10.6cm,则待测液的密度为多少
(3)为了提高自制密度计的精确度,请提出一条改进建议:
【答案】(1)∵漂浮
∴F浮=G=mg=0.2kg×10N/kg=2N
(2)∵F 浮’=ρ水gV 排’=103kg/m3×10N/kg×2×10-3m2×0.106m=2.12N
∴G 液=F 浮’-G=2.12N-2N=0.12N
∴
(3)将烧杯中的水换成密度更小的液体;减小密度计的横截面积;增加待测液的体积等
【解析】(1)当物体漂浮时,它受到的浮力等于重力,据此计算密度计受到的浮力;
(2)首先根据阿基米德原理F浮力=ρ液gV排计算出此时密度计受到的浮力,再根据二力平衡的知识计算出里面液体的重力,根据计算出里面液体的质量,最后利用密度公式计算液体密度。
(3)在测量液体密度时,密度计排开液体的体积越大,则浸入液体中的高度变化越大,那么密度计越精确,根据阿基米德原理F浮力=ρ液gV排分析即可。
【解答】(3)根据阿基米德原理F浮力=ρ液gV排=ρ液gSh排可知,要增大h排,可以减小液烧杯中液体的密度,或者减小密度计的横截面积,还可以增大待测液体的体积,从而增大浮力,进而增大h排。
11.(2022八上·慈溪月考)如图甲所示,水平放置的方形容器里有一个重为9 N、边长为10 cm的立方体物块M,M与容器底部不密合。以6 mL/s的恒定水流向容器内注水,容器中水的深度h随时间t的变化关系如图乙所示。求:
(1)当t=100 s时,物块M在水中处于 (选填“沉底”“悬浮"或“漂浮”)状态。
(2)当t=100 s时,水对容器底部的压力大小是多少
(3)图乙中a的值是多少
【答案】(1)漂浮
(2)当t=100s时,注入的水的体积V水=vt=6mL/s×100s=600mL=6×10-4m3,
则G水=ρ水gV水=1.0×103kg/m3×10N/kg×6×10-4m3=6N;
所以液体对底部的压力F=G水+GM=6N+9N=15N;
(3)当t=40s时,正好是物块M处于刚刚开始漂浮的状态,则F浮=GM=9N,
根据F浮=ρ液gV排可得:;
所以深度。
【解析】(1)已知物块M的边长,可求物块的体积,已知物块的重力可求物块的质量,根据密度公式可求物块的密度,再与水的密度进行比较,即可知道物体的在水中的浮沉状态;
(2)由于方形容器在水平方向上放置,则液体对底部的压力等于容器里液体和漂浮物体的总重力,所以根据V=vt求出当t=100s时注入的水的体积,然后求出水的重力,最后根据F=G水+GM即可求出压力;
(3)由乙可知:t=40s时,水的深度变化改变,即此时正好是物块M处于刚刚开始漂浮的状态,所以根据阿基米德原理F浮=ρ液gV排求出此时物块浸入水中的体积,最后根据计算出a的值。【解答】(1)物块M的体积V=(0.1m)3=0.001m3;
物块M的质量:;
物块M的密度;
即物块的密度小于水的密度,
根据图像可知,从40s~140s时,水面上升的速度减小,
即此时应该是物块离开容器底部,
那么当t=100s时,物体应该处于漂浮状态。
12.(2022八上·长兴月考)边长为10cm的正方体物块放入水平桌面上的圆柱形容器底部(如图甲所示),逐渐向容器内倒入适量水(水未溢出),测量容器内水的深度h,分别计算出物块对应受到的浮力F浮,并绘制了如图乙(实线)所示的图象。把水换成液体A重复上述实验,绘制了如图乙(虚线)所示的图像。
(1)由图乙可知,正方体物块受到的重力为 N。
(2)正方体物块的密度为多少?
(3)液体A的密度为多少?
【答案】(1)9
(2)正方体物块的体积V=L3=(10cm)3=1000cm3=0.001m3,
物体的密度:;
(3)由图象可知,当h=10cm以后物体在液体中受到的浮力F浮′=6N不变,
因F浮′<G,所以,物体处于沉底状态,
因物体完全浸没时排开液体的体积和自身的体积相等,
由F浮=ρ液gV排可得液体的密度为:。
【解析】(1)根据正方体物块的边长和水的深度从h=9cm以后物体受到的浮力9N不再发生变化,判断出物体的状态;物体处于漂浮状态时,受到的浮力和重力相等;
(2)知道边长可求体积,根据求出物体的密度;
(3)从图象中读出h=10cm以后物体在液体中受到的浮力,比较物体的重力和受到的浮力判断物体的状态,根据阿基米德原理F浮=ρ液gV排求出液体的密度。
【解答】(1)正方体物块的边长为10cm,由图象可知,水的深度从h=9cm以后物体受到的浮力9N不再发生变化,说明物体处于漂浮状态;
因物体漂浮时,受到的浮力和重力相等,
所以,物体的重力G=F浮=9N;
13.(2022八上·瑞安期中)某科学兴趣小组自制了一架简易液体密度计,使用说明书如下:
简易液体密度计使用说明书
结构 使用方法:1.弹簧测力计左边表示测力计示数,右边表示相应液体密度示数。2.将小金属块用细线挂于测力计挂钩处,测力计的示数为2牛,密度计的标记数值为0。3.将小金属块完全浸没于待测液体中。4.在右边刻度板上读出相应密度值。
(1)当金属块下表面刚好接触水面并下降,下列图中能正确反映这一过程中浮力F 和小金属 块下表面到水面距离h 的关系的图象是
A. B.
C. D.
(2)将小金属块(重为2牛,体积为40立方厘米)浸没在某种液体中时,左边测力计示数为1牛,则对应右边的密度值是多少千克/立方米?(写出计算过程)
(3)若将小金属块(重为2牛,体积为40立方厘米)换成大金属块(重5牛,体积为80立方厘米),已知两金属块材质不同,判断该密度计的量程和精确度将如何改变,并说明理由。
【答案】(1)D
(2)当金属块浸没时,其所受的浮力为:F浮=G-F拉==2牛-1牛=1牛(1分)
V排=V物=40厘米3=4x10-5米3
ρ=F浮/gV排=1牛/10牛/千克x4x10-5米3=2.5x103千克/米3
(3)精确度变大,量程变大。物块悬浮时,物块密度和液体密度相同,此时密度最大即为量程,由数据可知,大物块密度大,所以量程变大。根据F浮=G-F拉=G-p液gV排,当拉力变化量相同时,大物块比小物块体积大,V,变化量也大,所测液体密度的变化量小,所以精确度高。
【解析】(1)根据阿基米德原理F浮=ρ液gV排分析金属块受到浮力的变化;
(2)首先根据 F浮=G-F拉 计算出金属块受到的浮力,再根据阿基米德原理的变形式计算液体的密度。
(3)根据浮沉条件分析密度计量程的变化,根据“称量法” F浮=G-F拉 结合阿基米德原理F浮=ρ液gV排分析密度计分度值的变化,从而确定精确度的变化。
【解答】(1)随着金属块慢慢浸入水中时,它排开水的体积不断增大;当它完全浸没在水中时,它排开水的体积不变。根据阿基米德原理F浮=ρ液gV排可知,金属块受到的浮力先变大后不变。
典例分析
举一反三
典例分析
举一反三
典例分析
举一反三
典例分析
举一反三
课后巩固
同课章节目录
- 第1章 水和水的溶液
- 第1节 地球上的水
- 第2节 水的组成
- 第3节 水的浮力
- 第4节 物质在水中的分散状况
- 第5节 物质的溶解
- 第6节 物质的分离
- 第7节 水资源的利用、开发和保护
- 第2章 天气与气候
- 第1节 大气层
- 第2节 气温
- 第3节 大气的压强
- 第4节 风和降水
- 第5节 天气预报
- 第6节 气候和影响气候的因素
- 第7节 我国的气候特征与主要气象灾害
- 第3章 生命活动的调节
- 第1节 植物生命活动的调节
- 第2节 人体的激素调节
- 第3节 神经调节
- 第4节 动物的行为
- 第5节 体温的控制
- 第4章 电路探秘
- 第1节 电荷与电流
- 第2节 电流的测量
- 第3节 物质的导电性与电阻
- 第4节 变阻器
- 第5节 电压的测量
- 第6节 电流与电压、电阻的关系
- 第7节 电路分析与应用
- 研究性学习课题
- 一 测定本地区的“酸雨”情况及分析原因
- 二 太阳黑子活动与本地区降水的关系
- 三 训练小动物建立某种条件反射
- 四 调查在自然界或生命活动中的电现象
