24.1圆的有关性质 同步练习(含答案) 2023-2024学年人教版数学九年级上册
文档属性
| 名称 | 24.1圆的有关性质 同步练习(含答案) 2023-2024学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 277.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-15 18:46:07 | ||
图片预览


文档简介
24.1圆的有关性质 同步练习 2023-2024学年人教版数学九年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.如果两条弦相等,那么( )
A.这两条弦所对的弧相等 B.这两条弦所对的圆心角相等
C.这两条弦的弦心距相等 D.以上答案都不对
2.把地球和篮球的半径都增加一米,那么地球和篮球的大圆的周长也都增加了,谁增加得多一些呢( )
A.地球多 B.篮球多
C.一样多 D.不能确定
3.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( )
A.cm B.cm
C.cm或cm D.cm或cm
4.如图,在⊙O中,点A是 的中点,∠AOB=40°,则∠ADC的度数是( )
A.15° B.20° C.25° D.40°
5.如图,已知是的直径,过点C的弦平行于半径,若的度数是,则的度数是( )
A. B. C. D.
6.如图,AB是⊙O的直径,弦CD⊥AB于H,∠A=30°,CD=2 ,则⊙O的半径是( )
A.2 B. C.1 D.2
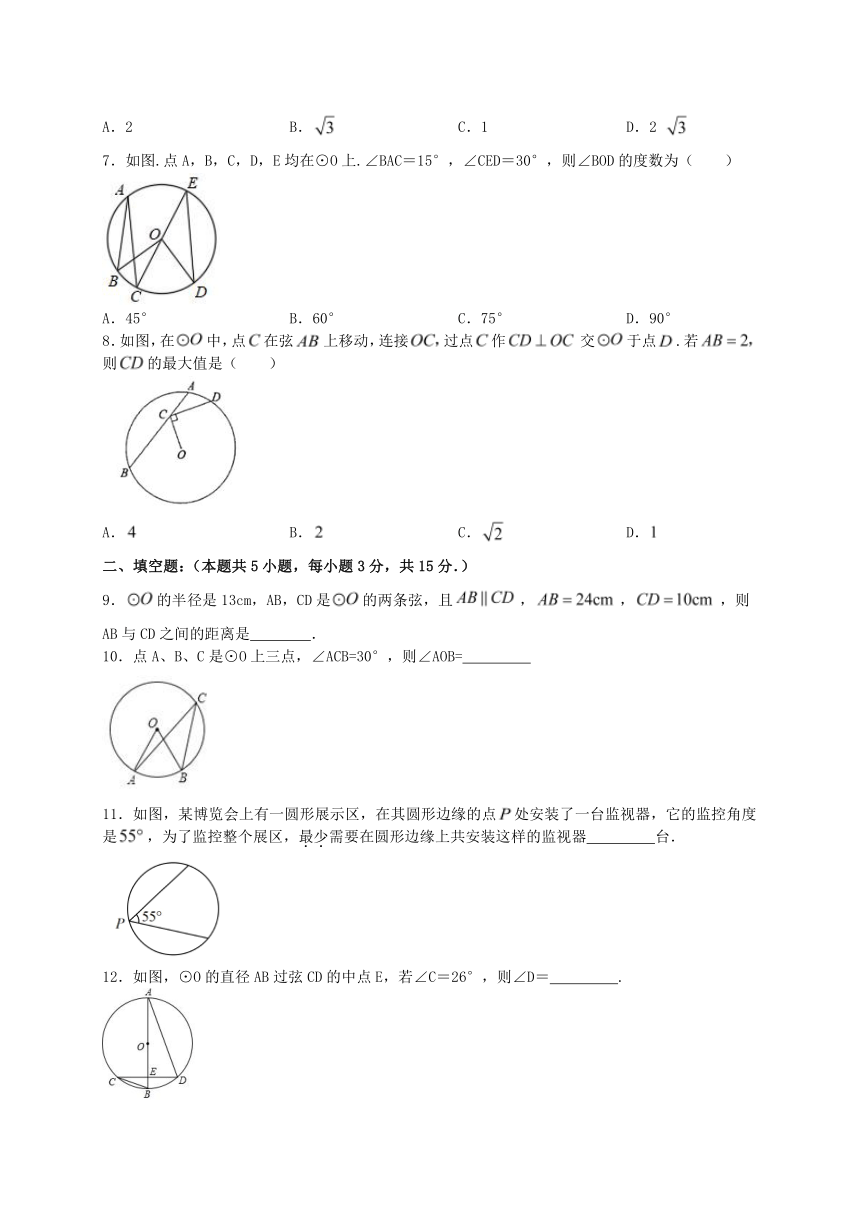
7.如图.点A,B,C,D,E均在⊙O上.∠BAC=15°,∠CED=30°,则∠BOD的度数为( )
A.45° B.60° C.75° D.90°
8.如图,在中,点在弦上移动,连接过点作交于点.若则的最大值是( )
A. B. C. D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.的半径是13cm,AB,CD是的两条弦,且,,,则AB与CD之间的距离是 .
10.点A、B、C是⊙O上三点,∠ACB=30°,则∠AOB=
11.如图,某博览会上有一圆形展示区,在其圆形边缘的点处安装了一台监视器,它的监控角度是,为了监控整个展区,最少需要在圆形边缘上共安装这样的监视器 台.
12.如图,⊙O的直径AB过弦CD的中点E,若∠C=26°,则∠D= .
13.如图,点 在 上,弦 垂直平分 ,垂足为 .若 ,则 的长为 .
三、解答题:(本题共5题,共45分)
14.一条排水管的截面如图所示.已知排水管的半径OB=10,水面宽AB=16.求截面圆心O到水面的距离.
15.如图,两个圆都以点O为圆心,大圆的弦交小圆于C,D两点,.求的长.
16.如图,的直径,、是圆上的两点,,,求,两点的距离.
17.如图,AB是⊙O的直径,点C,D是⊙O上的点,且OD∥BC,AC分别与BD,OD相交于点E,F.
(1)求证:点D为 的中点;
(2)若DF=7,AC=24,求⊙O的直径.
18.如图,都是的半径,.
(1)求证:;
(2)若,求的半径.
参考答案:
1.D 2.C 3.C 4.B 5.A 6.A 7.D 8.D
9.7cm或17cm
10.60°
11.4
12.64°
13.
14.解:过O作OC⊥AB垂足为C,
∵OC⊥AB
∴BC=8cm
在Rt△OBC中,由勾股定理得,
OC= = =6,
答:圆心O到水面的距离6.
15.证明:过点作,
,
,
又在中,
,
16.解:∵ ,
∴ ,
∵ 的直径 ,
∴ ,
∴
17.(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵OD∥BC,
∴∠OFA=90°,
∴OF⊥AC,
∴ = ,
即点D为 的中点
(2)解:OF⊥AC,
∴AF= AC=12,
∵DF=7,
∴OF=OD﹣DF=OA﹣7,
∵OA2=AF2+OF2,
∴OA2=122+(OA﹣7)2,
∴OA= ,
∴⊙O的直径为 .
18.(1)证明:∵,
∴,
∵,
∴,
,
.
(2)解:过点作半径于点E,则,
,
∴,
,
,
,
在中,
,
在中,,
,
,即的半径是
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.如果两条弦相等,那么( )
A.这两条弦所对的弧相等 B.这两条弦所对的圆心角相等
C.这两条弦的弦心距相等 D.以上答案都不对
2.把地球和篮球的半径都增加一米,那么地球和篮球的大圆的周长也都增加了,谁增加得多一些呢( )
A.地球多 B.篮球多
C.一样多 D.不能确定
3.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( )
A.cm B.cm
C.cm或cm D.cm或cm
4.如图,在⊙O中,点A是 的中点,∠AOB=40°,则∠ADC的度数是( )
A.15° B.20° C.25° D.40°
5.如图,已知是的直径,过点C的弦平行于半径,若的度数是,则的度数是( )
A. B. C. D.
6.如图,AB是⊙O的直径,弦CD⊥AB于H,∠A=30°,CD=2 ,则⊙O的半径是( )
A.2 B. C.1 D.2
7.如图.点A,B,C,D,E均在⊙O上.∠BAC=15°,∠CED=30°,则∠BOD的度数为( )
A.45° B.60° C.75° D.90°
8.如图,在中,点在弦上移动,连接过点作交于点.若则的最大值是( )
A. B. C. D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.的半径是13cm,AB,CD是的两条弦,且,,,则AB与CD之间的距离是 .
10.点A、B、C是⊙O上三点,∠ACB=30°,则∠AOB=
11.如图,某博览会上有一圆形展示区,在其圆形边缘的点处安装了一台监视器,它的监控角度是,为了监控整个展区,最少需要在圆形边缘上共安装这样的监视器 台.
12.如图,⊙O的直径AB过弦CD的中点E,若∠C=26°,则∠D= .
13.如图,点 在 上,弦 垂直平分 ,垂足为 .若 ,则 的长为 .
三、解答题:(本题共5题,共45分)
14.一条排水管的截面如图所示.已知排水管的半径OB=10,水面宽AB=16.求截面圆心O到水面的距离.
15.如图,两个圆都以点O为圆心,大圆的弦交小圆于C,D两点,.求的长.
16.如图,的直径,、是圆上的两点,,,求,两点的距离.
17.如图,AB是⊙O的直径,点C,D是⊙O上的点,且OD∥BC,AC分别与BD,OD相交于点E,F.
(1)求证:点D为 的中点;
(2)若DF=7,AC=24,求⊙O的直径.
18.如图,都是的半径,.
(1)求证:;
(2)若,求的半径.
参考答案:
1.D 2.C 3.C 4.B 5.A 6.A 7.D 8.D
9.7cm或17cm
10.60°
11.4
12.64°
13.
14.解:过O作OC⊥AB垂足为C,
∵OC⊥AB
∴BC=8cm
在Rt△OBC中,由勾股定理得,
OC= = =6,
答:圆心O到水面的距离6.
15.证明:过点作,
,
,
又在中,
,
16.解:∵ ,
∴ ,
∵ 的直径 ,
∴ ,
∴
17.(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵OD∥BC,
∴∠OFA=90°,
∴OF⊥AC,
∴ = ,
即点D为 的中点
(2)解:OF⊥AC,
∴AF= AC=12,
∵DF=7,
∴OF=OD﹣DF=OA﹣7,
∵OA2=AF2+OF2,
∴OA2=122+(OA﹣7)2,
∴OA= ,
∴⊙O的直径为 .
18.(1)证明:∵,
∴,
∵,
∴,
,
.
(2)解:过点作半径于点E,则,
,
∴,
,
,
,
在中,
,
在中,,
,
,即的半径是
同课章节目录
