22.3实际问题与二次函数 同步练习 (含答案) 2023-2024学年人教版数学九年级上册
文档属性
| 名称 | 22.3实际问题与二次函数 同步练习 (含答案) 2023-2024学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 469.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-15 18:45:47 | ||
图片预览


文档简介
22.3实际问题与二次函数 同步练习 2023-2024学年人教版数学九年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.某种商品的价格是元,准备进行两次降价.如果每次降价的百分率都是,经过两次降价后的价格(单位:元)随每次降价的百分率的变化而变化,则关于的函数解析式是( )
A. B. C. D.
2.正方形的边长为4,若边长增加x,那么面积增加y,则y关于x的函数表达式为( )
A. B. C. D.
3.在学校运动会上,一位运动员掷铅球,铅球的高与水平距离之间的函数关系式为,则此运动员的成绩是( )
A. B. C. D.
4.一个球从地面竖直向上弹起时的速度为10米/秒,经过t(秒)时球距离地面的高度h(米)适用公式h=10t-5t2,那么球弹起后又回到地面所花的时间t(秒)是( )
A.5 B.10 C.1 D.2
5.将进货单价为70元的某种商品按零售价100元/个售出时每天能卖出20个,若这种商品的零售价在一定范围内每降价1元,其日销售量就增加1个,为了获得最大利润,则应降价( )
A.5元 B.10元 C.15元 D.20元
6.某建筑物,从10m高的窗口A,用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面 m,则水流落地点B离墙的距离OB是( )
A.2m B.3m C.4m D.5m
7.某公园草坪的防护栏是由100段形状相同的抛物线形组成的.为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )
A.50m B.100m C.160m D.200m
8.如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC的边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则y与x函数关系的图象大致是( )
A. B. C. D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,当时,每天的销售量y(个)与销售价格x(元/个)之间满足关系式,设该食品零售店每天销售这款冷饮产品的利润为w元,则w与x之间的函数表达式为 .
10.如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,则水面下降1m时,水面宽度增加 m.
11.根据物理学规律,如果不考虑空气阻力,以的速度将小球沿与地面成角的方向击出,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系是,当飞行时间t为 s时,小球达到最高点.
12.如图,若被击打的小球飞行高度(单位:m)与飞行时间t(单位:s)之间具有的关系为,则小球从飞出到落地所用的时间为 s.
13.某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为 .
三、解答题:(本题共5题,共45分)
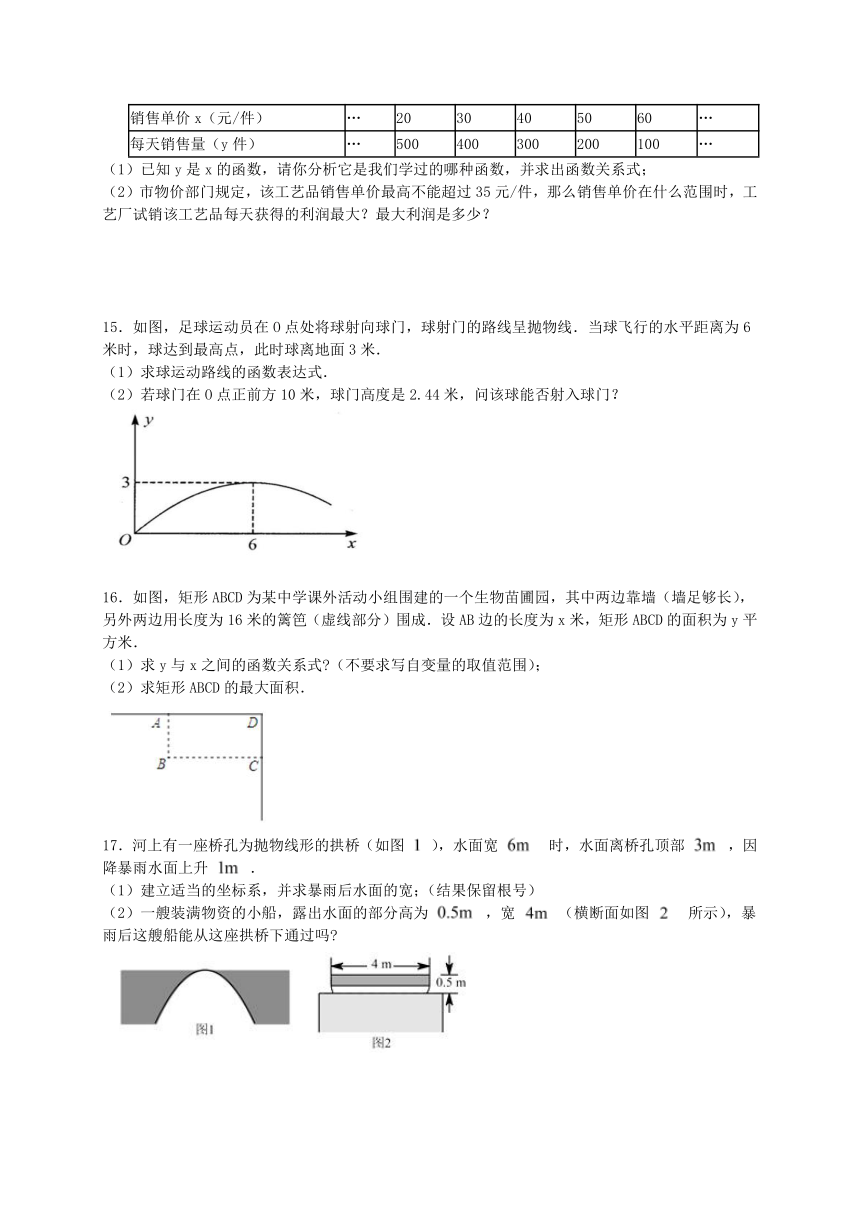
14.某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过调查,得到如下数据:
销售单价x(元/件) … 20 30 40 50 60 …
每天销售量(y件) … 500 400 300 200 100 …
(1)已知y是x的函数,请你分析它是我们学过的哪种函数,并求出函数关系式;
(2)市物价部门规定,该工艺品销售单价最高不能超过35元/件,那么销售单价在什么范围时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?
15.如图,足球运动员在O点处将球射向球门,球射门的路线呈抛物线.当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米.
(1)求球运动路线的函数表达式.
(2)若球门在O点正前方10米,球门高度是2.44米,问该球能否射入球门?
16.如图,矩形ABCD为某中学课外活动小组围建的一个生物苗圃园,其中两边靠墙(墙足够长),另外两边用长度为16米的篱笆(虚线部分)围成.设AB边的长度为x米,矩形ABCD的面积为y平方米.
(1)求y与x之间的函数关系式 (不要求写自变量的取值范围);
(2)求矩形ABCD的最大面积.
17.河上有一座桥孔为抛物线形的拱桥(如图 ),水面宽 时,水面离桥孔顶部 ,因降暴雨水面上升 .
(1)建立适当的坐标系,并求暴雨后水面的宽;(结果保留根号)
(2)一艘装满物资的小船,露出水面的部分高为 ,宽 (横断面如图 所示),暴雨后这艘船能从这座拱桥下通过吗
18.如图1所示,某公园有一个直径为16米的圆形喷水池,喷出的水柱为抛物线,且各方向喷出的水柱恰好落在水池内,过喷水管口所在铅垂线每一个截面均可得到两条关于对称的抛物线,如图2,以喷水池中心O为原点,喷水管口所在铅垂线为纵轴,建立平面直角坐标系.
(1)若喷出的水柱在距水池中心3米处达到最高,且高度为5米,求水柱所在抛物线的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
参考答案:
1.B 2.C 3.D 4.D 5.A 6.B 7.C 8.D
9.
10.(2 ﹣4)
11.2
12.5
13.0<a<6
14.解:(1)猜想y是x的一次函数.
设这个一次函数为y=kx+b(k≠0),
∵假设这个一次函数的图象经过(20,500),(30,400)这两点,
∴,解得,
∴y=﹣10x+700.
经验证,其他几个点也在该函数图象上,
故所求函数式是一次函数y=﹣10x+700.
(2)设工艺厂试销该工艺品每天获得的利润是W元,依题意得:
W=(x﹣10)(﹣10x+700)=﹣10x2+800x﹣7000=﹣10(x﹣40)2+9000,
∵﹣10<0,
∴抛物线开口向下,当x≤35时,W的值随着x的增大而增大,
∴销售单价定为35元/件时,工艺厂试销该工艺品每天获得的利润最大,
此时,W最大=8750元.
15.(1)解:由题意得,抛物线的顶点为(6,3)且经过原点,可设所求函数表达式为 y=a(x-6) 2+3,
把(0,0)代入上式,得 0=a(0-6) 2+3,解得a =- ,
∴球运动路线的函数表达式为: ;
(2)解:当 x=10 时,
∵ <2.44,
∴该球能射入球门.
16.解:(1)y=(16﹣x)x=﹣x2+16x;
(2)∵y=﹣x2+16x,
∴y=﹣(x﹣8)2+64.
∵0<x<16,
∴当x=8时,y的最大值为64.
答:矩形ABCD的最大面积为64平方米.
17.(1)解:如图,以抛物线的顶点为原点,以桥面为 轴,建立平面直角坐标系,由题意可知抛物线过点 ,设抛物线的函数表达式为: .把 代入 ,可求 ,则抛物线对应的函数表达式为 .
当水面上涨 米后,水面所在的位置为直线 ,
令 得,则 ,解得: , ,
∴此时水面宽为为: (米)
(2)解:由题意 :当船在桥拱的正中心航行时,船的边缘距抛物线对称轴水平距离为 米,在 中,令 得, ,
∵船上货物最高点距拱顶为: (米)且 ,
∴这艘船能从这座拱桥下通过.
18.(1)解:设水柱所在抛物线的函数表达式为,
将代入,得:,
解得:,
水柱所在抛物线的函数表达式为;
同理:
∴
(2)解:当时,则,
解得:(舍去),,
为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心7米以内
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.某种商品的价格是元,准备进行两次降价.如果每次降价的百分率都是,经过两次降价后的价格(单位:元)随每次降价的百分率的变化而变化,则关于的函数解析式是( )
A. B. C. D.
2.正方形的边长为4,若边长增加x,那么面积增加y,则y关于x的函数表达式为( )
A. B. C. D.
3.在学校运动会上,一位运动员掷铅球,铅球的高与水平距离之间的函数关系式为,则此运动员的成绩是( )
A. B. C. D.
4.一个球从地面竖直向上弹起时的速度为10米/秒,经过t(秒)时球距离地面的高度h(米)适用公式h=10t-5t2,那么球弹起后又回到地面所花的时间t(秒)是( )
A.5 B.10 C.1 D.2
5.将进货单价为70元的某种商品按零售价100元/个售出时每天能卖出20个,若这种商品的零售价在一定范围内每降价1元,其日销售量就增加1个,为了获得最大利润,则应降价( )
A.5元 B.10元 C.15元 D.20元
6.某建筑物,从10m高的窗口A,用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面 m,则水流落地点B离墙的距离OB是( )
A.2m B.3m C.4m D.5m
7.某公园草坪的防护栏是由100段形状相同的抛物线形组成的.为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )
A.50m B.100m C.160m D.200m
8.如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC的边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则y与x函数关系的图象大致是( )
A. B. C. D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,当时,每天的销售量y(个)与销售价格x(元/个)之间满足关系式,设该食品零售店每天销售这款冷饮产品的利润为w元,则w与x之间的函数表达式为 .
10.如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,则水面下降1m时,水面宽度增加 m.
11.根据物理学规律,如果不考虑空气阻力,以的速度将小球沿与地面成角的方向击出,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系是,当飞行时间t为 s时,小球达到最高点.
12.如图,若被击打的小球飞行高度(单位:m)与飞行时间t(单位:s)之间具有的关系为,则小球从飞出到落地所用的时间为 s.
13.某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为 .
三、解答题:(本题共5题,共45分)
14.某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过调查,得到如下数据:
销售单价x(元/件) … 20 30 40 50 60 …
每天销售量(y件) … 500 400 300 200 100 …
(1)已知y是x的函数,请你分析它是我们学过的哪种函数,并求出函数关系式;
(2)市物价部门规定,该工艺品销售单价最高不能超过35元/件,那么销售单价在什么范围时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?
15.如图,足球运动员在O点处将球射向球门,球射门的路线呈抛物线.当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米.
(1)求球运动路线的函数表达式.
(2)若球门在O点正前方10米,球门高度是2.44米,问该球能否射入球门?
16.如图,矩形ABCD为某中学课外活动小组围建的一个生物苗圃园,其中两边靠墙(墙足够长),另外两边用长度为16米的篱笆(虚线部分)围成.设AB边的长度为x米,矩形ABCD的面积为y平方米.
(1)求y与x之间的函数关系式 (不要求写自变量的取值范围);
(2)求矩形ABCD的最大面积.
17.河上有一座桥孔为抛物线形的拱桥(如图 ),水面宽 时,水面离桥孔顶部 ,因降暴雨水面上升 .
(1)建立适当的坐标系,并求暴雨后水面的宽;(结果保留根号)
(2)一艘装满物资的小船,露出水面的部分高为 ,宽 (横断面如图 所示),暴雨后这艘船能从这座拱桥下通过吗
18.如图1所示,某公园有一个直径为16米的圆形喷水池,喷出的水柱为抛物线,且各方向喷出的水柱恰好落在水池内,过喷水管口所在铅垂线每一个截面均可得到两条关于对称的抛物线,如图2,以喷水池中心O为原点,喷水管口所在铅垂线为纵轴,建立平面直角坐标系.
(1)若喷出的水柱在距水池中心3米处达到最高,且高度为5米,求水柱所在抛物线的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
参考答案:
1.B 2.C 3.D 4.D 5.A 6.B 7.C 8.D
9.
10.(2 ﹣4)
11.2
12.5
13.0<a<6
14.解:(1)猜想y是x的一次函数.
设这个一次函数为y=kx+b(k≠0),
∵假设这个一次函数的图象经过(20,500),(30,400)这两点,
∴,解得,
∴y=﹣10x+700.
经验证,其他几个点也在该函数图象上,
故所求函数式是一次函数y=﹣10x+700.
(2)设工艺厂试销该工艺品每天获得的利润是W元,依题意得:
W=(x﹣10)(﹣10x+700)=﹣10x2+800x﹣7000=﹣10(x﹣40)2+9000,
∵﹣10<0,
∴抛物线开口向下,当x≤35时,W的值随着x的增大而增大,
∴销售单价定为35元/件时,工艺厂试销该工艺品每天获得的利润最大,
此时,W最大=8750元.
15.(1)解:由题意得,抛物线的顶点为(6,3)且经过原点,可设所求函数表达式为 y=a(x-6) 2+3,
把(0,0)代入上式,得 0=a(0-6) 2+3,解得a =- ,
∴球运动路线的函数表达式为: ;
(2)解:当 x=10 时,
∵ <2.44,
∴该球能射入球门.
16.解:(1)y=(16﹣x)x=﹣x2+16x;
(2)∵y=﹣x2+16x,
∴y=﹣(x﹣8)2+64.
∵0<x<16,
∴当x=8时,y的最大值为64.
答:矩形ABCD的最大面积为64平方米.
17.(1)解:如图,以抛物线的顶点为原点,以桥面为 轴,建立平面直角坐标系,由题意可知抛物线过点 ,设抛物线的函数表达式为: .把 代入 ,可求 ,则抛物线对应的函数表达式为 .
当水面上涨 米后,水面所在的位置为直线 ,
令 得,则 ,解得: , ,
∴此时水面宽为为: (米)
(2)解:由题意 :当船在桥拱的正中心航行时,船的边缘距抛物线对称轴水平距离为 米,在 中,令 得, ,
∵船上货物最高点距拱顶为: (米)且 ,
∴这艘船能从这座拱桥下通过.
18.(1)解:设水柱所在抛物线的函数表达式为,
将代入,得:,
解得:,
水柱所在抛物线的函数表达式为;
同理:
∴
(2)解:当时,则,
解得:(舍去),,
为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心7米以内
同课章节目录
