2023-2024学年北京市重点大学附中八年级(上)开学数学试卷(含解析)
文档属性
| 名称 | 2023-2024学年北京市重点大学附中八年级(上)开学数学试卷(含解析) | 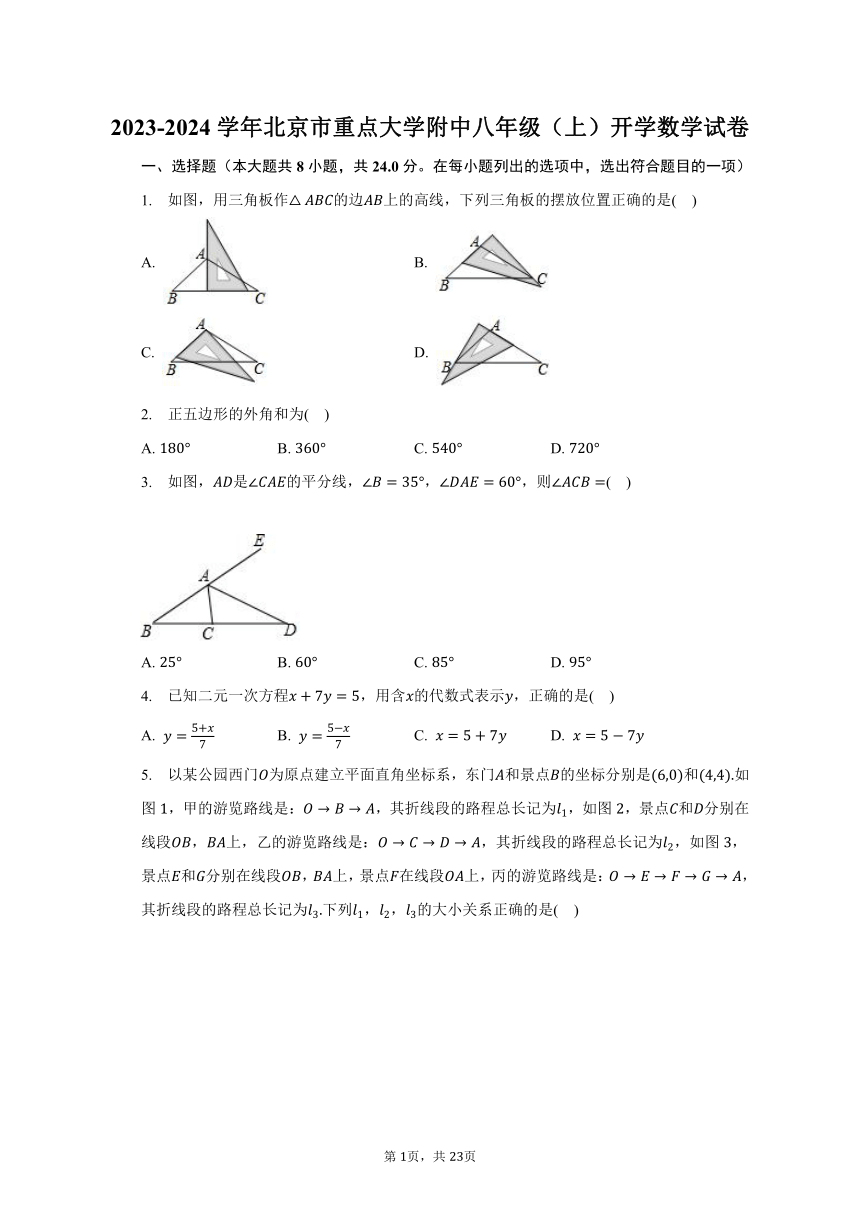 | |
| 格式 | docx | ||
| 文件大小 | 473.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 16:34:24 | ||
图片预览




文档简介
2023-2024学年北京市重点大学附中八年级(上)开学数学试卷
一、选择题(本大题共8小题,共24.0分。在每小题列出的选项中,选出符合题目的一项)
1. 如图,用三角板作的边上的高线,下列三角板的摆放位置正确的是( )
A. B.
C. D.
2. 正五边形的外角和为( )
A. B. C. D.
3. 如图,是的平分线,,,则( )
A. B. C. D.
4. 已知二元一次方程,用含的代数式表示,正确的是( )
A. B. C. D.
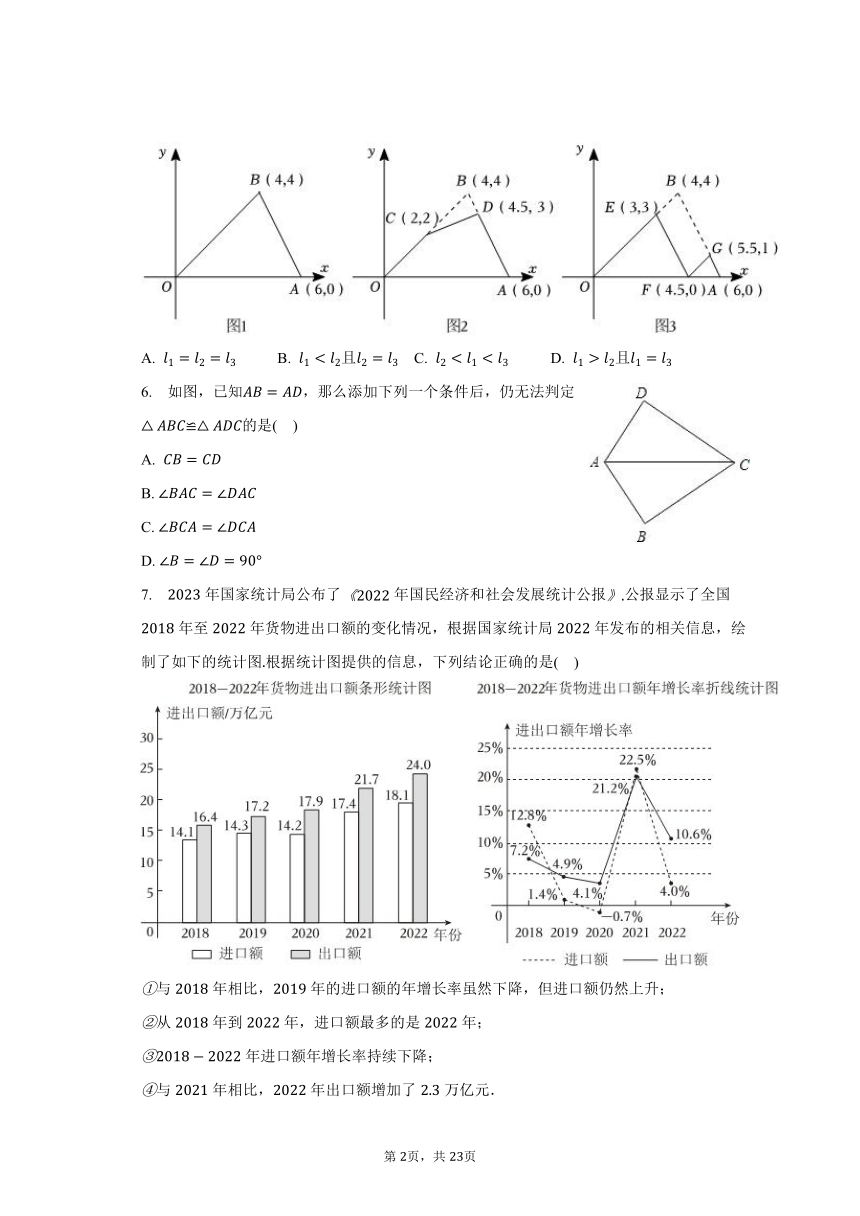
5. 以某公园西门为原点建立平面直角坐标系,东门和景点的坐标分别是和如图,甲的游览路线是:,其折线段的路程总长记为,如图,景点和分别在线段,上,乙的游览路线是:,其折线段的路程总长记为,如图,景点和分别在线段,上,景点在线段上,丙的游览路线是:,其折线段的路程总长记为下列,,的大小关系正确的是( )
A. B. 且 C. D. 且
6. 如图,已知,那么添加下列一个条件后,仍无法判定≌的是( )
A.
B.
C.
D.
7. 年国家统计局公布了年国民经济和社会发展统计公报公报显示了全国年至年货物进出口额的变化情况,根据国家统计局年发布的相关信息,绘制了如下的统计图根据统计图提供的信息,下列结论正确的是( )
与年相比,年的进口额的年增长率虽然下降,但进口额仍然上升;
从年到年,进口额最多的是年;
年进口额年增长率持续下降;
与年相比,年出口额增加了万亿元.
A. B. C. D.
8. 已知,则下列结论正确的是( )
A. B.
C. D.
二、填空题(本大题共8小题,共24.0分)
9. 已知关于的不等式的解集如图所示,那么的值是______ .
10. 计算: ______ .
11. 已知关于,的二元一次方程组满足,则的取值范围是______ .
12. 已知,,则用含的式子表示为______ .
13. 如图,在中,,,,平分则的度数为______ .
14. 在中,,点是上一点,将沿翻折后得到,边交于点若,.
则的度数为______ ;
若中有两个角相等,则 ______ .
15. 两个完全相同的正五边形都有一边在直线上,且有一个公共顶点,其摆放方式如图所示,则等于______度.
16. 某陶艺工坊有和两款电热窑,可以烧制不同尺寸的陶艺品,两款电热窑每次可同时放置陶艺品的尺寸和数量如表所示.
尺寸
数量个
款式 大 中 小
烧制一个大尺寸陶艺品的位置可替换为烧制两个中尺寸或六个小尺寸陶艺品,但烧制较小陶艺品的位置不能替换为烧制较大陶艺品.
某批次需要生产个大尺寸陶艺品,个中尺寸陶艺品,个小尺寸陶艺品.
烧制这批陶艺品,款电热窑至少使用______ 次;
若款电热窑每次烧制成本为元,款电热窑每次烧制成本为元,则烧制这批陶艺品成本最低为______ 元
三、解答题(本大题共6小题,共48.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
计算:
解不等式组:;
已知方程,当时,当时,求和的值.
18. 本小题分
已知如图所示,
画出中边上的高线,在内部作射线使得,交边于点,请你依题意补全图形;
判断与之间的关系,并说明理由.
19. 本小题分
如图,点,,,在直线上之间不能直接测量,点,在异侧,测得,,求证:.
20. 本小题分
在平面直角坐标系中,的三个顶点分别是,,.
在所给的图中,画出这个平面直角坐标系;
点经过平移后对应点为,将作同样的平移得到,画出平移后的;
在的条件下,点在直线上,若,直接写出点的坐标;
在的条件下,已知,点,点,所围成的区域内包括边界恰有个整点,求的取值范围.
21. 本小题分
如图,中,,,点为射线上一动点,连结,作且.
如图,过点作交于点,求证:;
如图,连结交于点,若,,求证:点为中点;
当点在射线上,连结与直线交于点,若,,则______直接写出结果
22. 本小题分
已知点和图形,为图形上一点,若存在点,使得点为线段的中点不重合,则称点为图形关于点的倍点.
如图,在平面直角坐标系中,点,,,.
若点的坐标为,则在,,中,是正方形关于点的倍点的是______ ;
点的坐标为,若在第一三象限的角平分线才存在正方形关于点的倍点,求的取值范围;
已知点,,若线段上的所有点均可成为正方形关于其边上某一点的倍点,直接写出点的取值范围.
答案和解析
1.【答案】
【解析】解:作的是边上的高,作的不是三角形的高,作的是边上的高,所以都不是的边上的高,而作的是过顶点且与垂直的线,是边上的高线,符合题意.
故选:.
根据高线的定义即可得出结论.
本题考查的是三角形的高的定义,熟知三角形高线的定义是解答此题的关键.
2.【答案】
【解析】解:任意多边形的外角和都是,
故正五边形的外角和的度数为.
故选:.
根据多边形的外角和等于,即可求解.
本题主要考查多边形的外角和定理,解答本题的关键是掌握任意多边形的外角和都是.
3.【答案】
【解析】【解答】解:是的平分线,
,
,
故选:.
【分析】
本题考查的是三角形的外角的性质、角平分线的定义,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.
根据角平分线的定义得到,根据三角形的外角的性质计算即可.
4.【答案】
【解析】解:,
,
则.
故选:.
要用的代数式表示,先移项,再将系数化为即可.
本题主要考查了解二元一次方程,掌握解二元一次方程的步骤是关键.
5.【答案】
【解析】解:根据题意可得,,
;
将线段平移,可得到线段,线段移可得到线段,
,,
,
,
故选:.
根据三角形三边的关系即可证明,根据平移的性质可证明.
本题考查了三角形三边关系平移的性质,题目新颖,灵活运用所学知识是关键
6.【答案】
【解析】【分析】
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:、、、、注意:、不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
【解答】解:、添加,根据,能判定≌,故A选项不符合题意;
B、添加,根据,能判定≌,故B选项不符合题意;
C、添加时,不能判定≌,故C选项符合题意;
D、添加,根据,能判定≌,故D选项不符合题意.
故选C.
7.【答案】
【解析】解:由条形图与折线图可知,的进口额为万亿元,进口额的年增长率为,的进口额为万亿元,进口额的年增长率为,所以与年相比,年的进口额的年增长率虽然下降,但进口额仍然上升,故结论正确,符合题意;
由条形图可知,从年到年,进口额最多的是年,为万亿元,故结论正确,符合题意;
由折线图可知,年进口额年增长率先下降再上升再下降,故结论错误,不符合题意;
由条形图可知,与年相比,年出口额增加了万亿元,故结论正确,符合题意;
故选:.
根据条形统计图与折线统计图所给的信息进行求解即可.
本题考查的是条形统计图和折线统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据,折线统计图表示的是事物的变化情况.
8.【答案】
【解析】解:,
,
,
,
故选:.
根据不等式的性质,进行计算即可解答.
本题考查了不等式的性质,熟练掌握不等式的性质是解题的关键.
9.【答案】
【解析】解:不等式的解集为:,
又不等式的在数轴上的解集为,
,
故.
故答案为:.
不等式的解集是,数轴表示的解集是则,.
本题考查不等式的解集在数轴上的表示方法,正确计算不等式的值是解题关键.
10.【答案】
【解析】解:原式
.
先把二次根式化成最简形式,然后合并同类二次根式即可.
本题主要考查了二次根式的计算,解题关键是把二次根式化成最简二次根式.
11.【答案】
【解析】【分析】
本题考查解一元一次不等式、二元一次方程组的解,解答本题的关键是明确利用加减消元法得到的值.
根据方程组的特点,用第一个方程减第二个方程,即可得到,再根据,即可得到,从而可以求得的取值范围.
【解答】
解:,
,得,
,
,
解得,
故答案为.
12.【答案】
【解析】解:,
,
,
,
,
.
故答案为:.
根据已知条件得出,再代入进行计算,即可得出答案.
此题考查了列代数式,解题的关键是根据已知条件得出;一定注意是用含的式子表示.
13.【答案】
【解析】解:在中,,,
,
,
,
在中,,
平分.
,
.
故答案为:.
先求出,,再求出即可解答.
本题考查三角形内角和定理和外角的性质,熟练掌握以上知识是解题.
14.【答案】
【解析】解:,,
,,
故答案为:;
,
,
,
,
,
,
当时,,
解得,,
当时,,
解得,,
,
不合题意,故舍去,
当,,
解得,,
,
不合题意舍去.
综上可知,存在这样的的值,使得中有两个角相等,且.
故答案为:.
根据三角形内角和定理分别求出,即可;
分、、三种情况,列方程解答即可.
本题考查的是翻转变换、三角形内角和定理、等腰三角形的性质、平行线的判定,掌握三角形内角和等于、翻转变换的性质是解题的关键.
15.【答案】
【解析】解:如图,
由正五边形的内角和,得,
,
.
,
故答案为:.
根据多边形的内角和,可得,,,,根据等腰三角形的内角和,可得,根据角的和差,可得答案.
本题考查了多边形的内角与外角,利用多边形的内角和得出每个内角是解题关键.
16.【答案】
【解析】解:设烧制这批陶艺品需使用款电热窑次,
根据题意得:,
解得:,
又为正整数,
的最小值为,
款电热窑至少使用次.
故答案为:;
当使用款电热窑烧制次时,将第次的个大尺寸陶艺品位置替换成个中尺寸陶艺品,个大尺寸陶艺品位置替换成个小尺寸陶艺品,
还需烧制中尺寸陶艺品个,小尺寸陶艺品个,
又款电热窑一次可烧制个中尺寸陶艺品,个小尺寸陶艺品,
还需使用款电热窑烧制一次,
此方案所需成本为元.
当款电热窑使用次时,所需成本为元.
,
烧制这批陶艺品成本最低为元.
故答案为:.
设烧制这批陶艺品需使用款电热窑次,由烧制大尺寸陶艺品只能使用款电热窑及烧制的大尺寸陶艺品不少于个,可得出关于的一元一次不等式,解之可得出的取值范围,再取其中的最小整数值,即可得出结论;
当使用款电热窑烧制次时,可求出恰好还需使用款电热窑烧制一次,求出该方案的成本,再求出使用款电热窑烧制次所需成本,比较后即可得出结论.
本题考查了一元一次不等式的应用以及有理数的混合运算,解题的关键是:根据各数量之间的关系,正确列出一元一次不等式;根据各数量之间的关系,求出各烧制方案所需的成本.
17.【答案】解:,
解不等式,得,
解不等式,得.
故不等式组的解集是;
由题意得,,
,得,
解得,
把代入,得,,
解得.
故,.
【解析】先求出每个不等式的解集,再求出不等式组的解集即可;
根据题意列出关于、的二元一次方程组,再解方程组即可.
本题考查的是解二元一次方程组和解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
18.【答案】解:以为圆心,任意长为半径作弧交于,,作线段的垂直平分线交于,作线段的垂直平分线交于,作射线,如图:
线段即为中边上的高线,射线即为所求;
,理由如下:
是高,
,
,
,
,
,即.
【解析】以为圆心,任意长为半径作弧交于,,作线段的垂直平分线交于,作线段的垂直平分线交于,作射线,线段即为中边上的高线,射线即为所求;
根据是高,可得,而,即得.
本题考查作图复杂作图,解题的关键是掌握作线段的垂直平分线的方法.
19.【答案】证明:,
,
在与中
,
≌,
.
,即.
【解析】先证明,再根据即可证明.
本题考查全等三角形的判定和性质,解题的关键是掌握三角形全等的判定定理,正确寻找三角形全等所需的条件,属于基础题,中考常考题型.
20.【答案】解:如图,
如图:即为所求;
点在直线上,若,
设点的坐标为,
当点在之间时,,,
,
解得:,
点的坐标为,
当点在点下方时,,,
,
解得:,
点的坐标为,
综上所述,点的坐标为或.
如图,
点,点,且,
点与点关于直线对称,
若所围成的区域内包括边界恰有个整点,则需要两点之间恰好有个整点,
当,时,两点之间恰好有个整点,此时;
当,时,两点之间恰好有个整点,此时;
故当点,点分别在,之间时不包含,满足要求;
的取值范围是.
【解析】根据三个点的坐标作图即可;
将点、分别向右平移格、向下平移格得到其对应点,再首尾顺次连接即可;
设点的坐标为,分两种情况列出方程可得出答案;
画出图形,由题意可知点与点关于直线对称,求出的值可得出答案.
本题考查作图平移变换,坐标与图形的性质,解题的关键是掌握平移变换的定义和性质,并据此得出变换后的对应点.
21.【答案】证明:,
,
,
同理,,
,
在和中,
≌,
,
,
或
作于,
由得,,,
在和中,
,
≌,
,,
,
,
同理,当点在线段上时,
【解析】证明≌,根据全等三角形的性质得到,等量代换证明结论;
作于,证明≌,得到,求出,的长,得到答案;
过作的延长线交于点,根据全等三角形的性质得到,,代入计算即可.
本题考查的是全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理是解题的关键.
当点在的延长线上时,过作的延长线交于点,
,,
由知:≌,≌,
,,
,
,
同理,当点在线段上时,
22.【答案】,
【解析】解:设是正方形上一点,点的坐标为,根据“倍点”定义,若是图形关于点的倍点,
则有:,
解得:,
在正方形上,
是正方形关于点的倍点;
若是图形关于点的倍点,
则有:,
解得:,
不在正方形上,
不是正方形关于点的倍点;
若是图形关于点的倍点,
则有:,
解得:,
在正方形上,
是正方形关于点的倍点;
故答案为:,.
角平分线上的点到两边的距离相等,
故第一,三象限的角平分线经过点,,
设第一,三象限的角平分线的解析式为,
将代入,
解得:,
故第一,三象限的角平分线的解析式;
设直线上存在的点的坐标为,正方形上的点的坐标为,
则 ,
解得:,
点在直线上,则,
即,
正方形上的点的坐标为,
且,,,,
,即,
解得:.
设直线的解析式为,将点,的坐标代入,
,
解得:,
直线的解析式为;
线段上的所有点均可成为正方形关于其边上某一点的倍点,
当线段上的所有点是正方形关于其边上点的倍点时,当点与点重合时,正方形上的点关于点的倍点在如图四边形上,
同理,当点在正方形的顶点上时,对应的倍点图形为:
当点在正方形的边上时,正方形上的点关于点的倍点在如图四边形上,
同理,当点在正方形的四条边上时,对应的倍点图形为:
综上,正方形关于其边上某一点的倍点所在范围为如图虚线框内减去部分:
直线的解析式为,故线段上的所有点均可成为正方形关于其边上某一点的倍点,如图:
此时或.
设是正方形上一点,根据“倍点”的定义,代入求得点的坐标,结合题意逐一判断即可;
先根据角平分线的性质求得第一,三象限的角平分线的解析式;设直线上存在的点的坐标为,正方形上的点的坐标为,根据“倍点”的定义,和一次函数图象上点的特征,求得,根据正方形上点的坐标可得,即可求解;
先求得直线的解析式为;根据题意分析得出倍点所在的范围,结合题意即可得到答案.
本题考查了一次函数的性质,中点坐标公式及“倍点”的定义等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
第1页,共1页
一、选择题(本大题共8小题,共24.0分。在每小题列出的选项中,选出符合题目的一项)
1. 如图,用三角板作的边上的高线,下列三角板的摆放位置正确的是( )
A. B.
C. D.
2. 正五边形的外角和为( )
A. B. C. D.
3. 如图,是的平分线,,,则( )
A. B. C. D.
4. 已知二元一次方程,用含的代数式表示,正确的是( )
A. B. C. D.
5. 以某公园西门为原点建立平面直角坐标系,东门和景点的坐标分别是和如图,甲的游览路线是:,其折线段的路程总长记为,如图,景点和分别在线段,上,乙的游览路线是:,其折线段的路程总长记为,如图,景点和分别在线段,上,景点在线段上,丙的游览路线是:,其折线段的路程总长记为下列,,的大小关系正确的是( )
A. B. 且 C. D. 且
6. 如图,已知,那么添加下列一个条件后,仍无法判定≌的是( )
A.
B.
C.
D.
7. 年国家统计局公布了年国民经济和社会发展统计公报公报显示了全国年至年货物进出口额的变化情况,根据国家统计局年发布的相关信息,绘制了如下的统计图根据统计图提供的信息,下列结论正确的是( )
与年相比,年的进口额的年增长率虽然下降,但进口额仍然上升;
从年到年,进口额最多的是年;
年进口额年增长率持续下降;
与年相比,年出口额增加了万亿元.
A. B. C. D.
8. 已知,则下列结论正确的是( )
A. B.
C. D.
二、填空题(本大题共8小题,共24.0分)
9. 已知关于的不等式的解集如图所示,那么的值是______ .
10. 计算: ______ .
11. 已知关于,的二元一次方程组满足,则的取值范围是______ .
12. 已知,,则用含的式子表示为______ .
13. 如图,在中,,,,平分则的度数为______ .
14. 在中,,点是上一点,将沿翻折后得到,边交于点若,.
则的度数为______ ;
若中有两个角相等,则 ______ .
15. 两个完全相同的正五边形都有一边在直线上,且有一个公共顶点,其摆放方式如图所示,则等于______度.
16. 某陶艺工坊有和两款电热窑,可以烧制不同尺寸的陶艺品,两款电热窑每次可同时放置陶艺品的尺寸和数量如表所示.
尺寸
数量个
款式 大 中 小
烧制一个大尺寸陶艺品的位置可替换为烧制两个中尺寸或六个小尺寸陶艺品,但烧制较小陶艺品的位置不能替换为烧制较大陶艺品.
某批次需要生产个大尺寸陶艺品,个中尺寸陶艺品,个小尺寸陶艺品.
烧制这批陶艺品,款电热窑至少使用______ 次;
若款电热窑每次烧制成本为元,款电热窑每次烧制成本为元,则烧制这批陶艺品成本最低为______ 元
三、解答题(本大题共6小题,共48.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
计算:
解不等式组:;
已知方程,当时,当时,求和的值.
18. 本小题分
已知如图所示,
画出中边上的高线,在内部作射线使得,交边于点,请你依题意补全图形;
判断与之间的关系,并说明理由.
19. 本小题分
如图,点,,,在直线上之间不能直接测量,点,在异侧,测得,,求证:.
20. 本小题分
在平面直角坐标系中,的三个顶点分别是,,.
在所给的图中,画出这个平面直角坐标系;
点经过平移后对应点为,将作同样的平移得到,画出平移后的;
在的条件下,点在直线上,若,直接写出点的坐标;
在的条件下,已知,点,点,所围成的区域内包括边界恰有个整点,求的取值范围.
21. 本小题分
如图,中,,,点为射线上一动点,连结,作且.
如图,过点作交于点,求证:;
如图,连结交于点,若,,求证:点为中点;
当点在射线上,连结与直线交于点,若,,则______直接写出结果
22. 本小题分
已知点和图形,为图形上一点,若存在点,使得点为线段的中点不重合,则称点为图形关于点的倍点.
如图,在平面直角坐标系中,点,,,.
若点的坐标为,则在,,中,是正方形关于点的倍点的是______ ;
点的坐标为,若在第一三象限的角平分线才存在正方形关于点的倍点,求的取值范围;
已知点,,若线段上的所有点均可成为正方形关于其边上某一点的倍点,直接写出点的取值范围.
答案和解析
1.【答案】
【解析】解:作的是边上的高,作的不是三角形的高,作的是边上的高,所以都不是的边上的高,而作的是过顶点且与垂直的线,是边上的高线,符合题意.
故选:.
根据高线的定义即可得出结论.
本题考查的是三角形的高的定义,熟知三角形高线的定义是解答此题的关键.
2.【答案】
【解析】解:任意多边形的外角和都是,
故正五边形的外角和的度数为.
故选:.
根据多边形的外角和等于,即可求解.
本题主要考查多边形的外角和定理,解答本题的关键是掌握任意多边形的外角和都是.
3.【答案】
【解析】【解答】解:是的平分线,
,
,
故选:.
【分析】
本题考查的是三角形的外角的性质、角平分线的定义,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.
根据角平分线的定义得到,根据三角形的外角的性质计算即可.
4.【答案】
【解析】解:,
,
则.
故选:.
要用的代数式表示,先移项,再将系数化为即可.
本题主要考查了解二元一次方程,掌握解二元一次方程的步骤是关键.
5.【答案】
【解析】解:根据题意可得,,
;
将线段平移,可得到线段,线段移可得到线段,
,,
,
,
故选:.
根据三角形三边的关系即可证明,根据平移的性质可证明.
本题考查了三角形三边关系平移的性质,题目新颖,灵活运用所学知识是关键
6.【答案】
【解析】【分析】
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:、、、、注意:、不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
【解答】解:、添加,根据,能判定≌,故A选项不符合题意;
B、添加,根据,能判定≌,故B选项不符合题意;
C、添加时,不能判定≌,故C选项符合题意;
D、添加,根据,能判定≌,故D选项不符合题意.
故选C.
7.【答案】
【解析】解:由条形图与折线图可知,的进口额为万亿元,进口额的年增长率为,的进口额为万亿元,进口额的年增长率为,所以与年相比,年的进口额的年增长率虽然下降,但进口额仍然上升,故结论正确,符合题意;
由条形图可知,从年到年,进口额最多的是年,为万亿元,故结论正确,符合题意;
由折线图可知,年进口额年增长率先下降再上升再下降,故结论错误,不符合题意;
由条形图可知,与年相比,年出口额增加了万亿元,故结论正确,符合题意;
故选:.
根据条形统计图与折线统计图所给的信息进行求解即可.
本题考查的是条形统计图和折线统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据,折线统计图表示的是事物的变化情况.
8.【答案】
【解析】解:,
,
,
,
故选:.
根据不等式的性质,进行计算即可解答.
本题考查了不等式的性质,熟练掌握不等式的性质是解题的关键.
9.【答案】
【解析】解:不等式的解集为:,
又不等式的在数轴上的解集为,
,
故.
故答案为:.
不等式的解集是,数轴表示的解集是则,.
本题考查不等式的解集在数轴上的表示方法,正确计算不等式的值是解题关键.
10.【答案】
【解析】解:原式
.
先把二次根式化成最简形式,然后合并同类二次根式即可.
本题主要考查了二次根式的计算,解题关键是把二次根式化成最简二次根式.
11.【答案】
【解析】【分析】
本题考查解一元一次不等式、二元一次方程组的解,解答本题的关键是明确利用加减消元法得到的值.
根据方程组的特点,用第一个方程减第二个方程,即可得到,再根据,即可得到,从而可以求得的取值范围.
【解答】
解:,
,得,
,
,
解得,
故答案为.
12.【答案】
【解析】解:,
,
,
,
,
.
故答案为:.
根据已知条件得出,再代入进行计算,即可得出答案.
此题考查了列代数式,解题的关键是根据已知条件得出;一定注意是用含的式子表示.
13.【答案】
【解析】解:在中,,,
,
,
,
在中,,
平分.
,
.
故答案为:.
先求出,,再求出即可解答.
本题考查三角形内角和定理和外角的性质,熟练掌握以上知识是解题.
14.【答案】
【解析】解:,,
,,
故答案为:;
,
,
,
,
,
,
当时,,
解得,,
当时,,
解得,,
,
不合题意,故舍去,
当,,
解得,,
,
不合题意舍去.
综上可知,存在这样的的值,使得中有两个角相等,且.
故答案为:.
根据三角形内角和定理分别求出,即可;
分、、三种情况,列方程解答即可.
本题考查的是翻转变换、三角形内角和定理、等腰三角形的性质、平行线的判定,掌握三角形内角和等于、翻转变换的性质是解题的关键.
15.【答案】
【解析】解:如图,
由正五边形的内角和,得,
,
.
,
故答案为:.
根据多边形的内角和,可得,,,,根据等腰三角形的内角和,可得,根据角的和差,可得答案.
本题考查了多边形的内角与外角,利用多边形的内角和得出每个内角是解题关键.
16.【答案】
【解析】解:设烧制这批陶艺品需使用款电热窑次,
根据题意得:,
解得:,
又为正整数,
的最小值为,
款电热窑至少使用次.
故答案为:;
当使用款电热窑烧制次时,将第次的个大尺寸陶艺品位置替换成个中尺寸陶艺品,个大尺寸陶艺品位置替换成个小尺寸陶艺品,
还需烧制中尺寸陶艺品个,小尺寸陶艺品个,
又款电热窑一次可烧制个中尺寸陶艺品,个小尺寸陶艺品,
还需使用款电热窑烧制一次,
此方案所需成本为元.
当款电热窑使用次时,所需成本为元.
,
烧制这批陶艺品成本最低为元.
故答案为:.
设烧制这批陶艺品需使用款电热窑次,由烧制大尺寸陶艺品只能使用款电热窑及烧制的大尺寸陶艺品不少于个,可得出关于的一元一次不等式,解之可得出的取值范围,再取其中的最小整数值,即可得出结论;
当使用款电热窑烧制次时,可求出恰好还需使用款电热窑烧制一次,求出该方案的成本,再求出使用款电热窑烧制次所需成本,比较后即可得出结论.
本题考查了一元一次不等式的应用以及有理数的混合运算,解题的关键是:根据各数量之间的关系,正确列出一元一次不等式;根据各数量之间的关系,求出各烧制方案所需的成本.
17.【答案】解:,
解不等式,得,
解不等式,得.
故不等式组的解集是;
由题意得,,
,得,
解得,
把代入,得,,
解得.
故,.
【解析】先求出每个不等式的解集,再求出不等式组的解集即可;
根据题意列出关于、的二元一次方程组,再解方程组即可.
本题考查的是解二元一次方程组和解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
18.【答案】解:以为圆心,任意长为半径作弧交于,,作线段的垂直平分线交于,作线段的垂直平分线交于,作射线,如图:
线段即为中边上的高线,射线即为所求;
,理由如下:
是高,
,
,
,
,
,即.
【解析】以为圆心,任意长为半径作弧交于,,作线段的垂直平分线交于,作线段的垂直平分线交于,作射线,线段即为中边上的高线,射线即为所求;
根据是高,可得,而,即得.
本题考查作图复杂作图,解题的关键是掌握作线段的垂直平分线的方法.
19.【答案】证明:,
,
在与中
,
≌,
.
,即.
【解析】先证明,再根据即可证明.
本题考查全等三角形的判定和性质,解题的关键是掌握三角形全等的判定定理,正确寻找三角形全等所需的条件,属于基础题,中考常考题型.
20.【答案】解:如图,
如图:即为所求;
点在直线上,若,
设点的坐标为,
当点在之间时,,,
,
解得:,
点的坐标为,
当点在点下方时,,,
,
解得:,
点的坐标为,
综上所述,点的坐标为或.
如图,
点,点,且,
点与点关于直线对称,
若所围成的区域内包括边界恰有个整点,则需要两点之间恰好有个整点,
当,时,两点之间恰好有个整点,此时;
当,时,两点之间恰好有个整点,此时;
故当点,点分别在,之间时不包含,满足要求;
的取值范围是.
【解析】根据三个点的坐标作图即可;
将点、分别向右平移格、向下平移格得到其对应点,再首尾顺次连接即可;
设点的坐标为,分两种情况列出方程可得出答案;
画出图形,由题意可知点与点关于直线对称,求出的值可得出答案.
本题考查作图平移变换,坐标与图形的性质,解题的关键是掌握平移变换的定义和性质,并据此得出变换后的对应点.
21.【答案】证明:,
,
,
同理,,
,
在和中,
≌,
,
,
或
作于,
由得,,,
在和中,
,
≌,
,,
,
,
同理,当点在线段上时,
【解析】证明≌,根据全等三角形的性质得到,等量代换证明结论;
作于,证明≌,得到,求出,的长,得到答案;
过作的延长线交于点,根据全等三角形的性质得到,,代入计算即可.
本题考查的是全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理是解题的关键.
当点在的延长线上时,过作的延长线交于点,
,,
由知:≌,≌,
,,
,
,
同理,当点在线段上时,
22.【答案】,
【解析】解:设是正方形上一点,点的坐标为,根据“倍点”定义,若是图形关于点的倍点,
则有:,
解得:,
在正方形上,
是正方形关于点的倍点;
若是图形关于点的倍点,
则有:,
解得:,
不在正方形上,
不是正方形关于点的倍点;
若是图形关于点的倍点,
则有:,
解得:,
在正方形上,
是正方形关于点的倍点;
故答案为:,.
角平分线上的点到两边的距离相等,
故第一,三象限的角平分线经过点,,
设第一,三象限的角平分线的解析式为,
将代入,
解得:,
故第一,三象限的角平分线的解析式;
设直线上存在的点的坐标为,正方形上的点的坐标为,
则 ,
解得:,
点在直线上,则,
即,
正方形上的点的坐标为,
且,,,,
,即,
解得:.
设直线的解析式为,将点,的坐标代入,
,
解得:,
直线的解析式为;
线段上的所有点均可成为正方形关于其边上某一点的倍点,
当线段上的所有点是正方形关于其边上点的倍点时,当点与点重合时,正方形上的点关于点的倍点在如图四边形上,
同理,当点在正方形的顶点上时,对应的倍点图形为:
当点在正方形的边上时,正方形上的点关于点的倍点在如图四边形上,
同理,当点在正方形的四条边上时,对应的倍点图形为:
综上,正方形关于其边上某一点的倍点所在范围为如图虚线框内减去部分:
直线的解析式为,故线段上的所有点均可成为正方形关于其边上某一点的倍点,如图:
此时或.
设是正方形上一点,根据“倍点”的定义,代入求得点的坐标,结合题意逐一判断即可;
先根据角平分线的性质求得第一,三象限的角平分线的解析式;设直线上存在的点的坐标为,正方形上的点的坐标为,根据“倍点”的定义,和一次函数图象上点的特征,求得,根据正方形上点的坐标可得,即可求解;
先求得直线的解析式为;根据题意分析得出倍点所在的范围,结合题意即可得到答案.
本题考查了一次函数的性质,中点坐标公式及“倍点”的定义等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
第1页,共1页
同课章节目录
