4.4 探索三角形相似的条件同步练习(无答案)2023-2024学年北师大版九年级数学上册
文档属性
| 名称 | 4.4 探索三角形相似的条件同步练习(无答案)2023-2024学年北师大版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 153.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 18:38:39 | ||
图片预览


文档简介
北师大版九年级上册4.4 探索三角形相似的条件
一、选择题
1. 下列命题中正确的有( )
①有一个角等于80°的两个等腰三角形相似;
②两边对应成比例的两个等腰三角形相似;
③有一个角对应相等的两个等腰三角形相似;
④底边对应相等的两个等腰三角形相似.
A.0个 B.1个 C.2个 D.3个
2. 矩形ABCD中,点E、F分别在AD、CD上,且∠BEF=90 ,则三角形Ⅰ,Ⅱ,Ⅲ,Ⅳ一定相似的是 ( ).
A.Ⅰ和Ⅱ B.Ⅰ和Ⅲ C.Ⅰ和Ⅳ D.Ⅲ和Ⅳ
3. 已知△ABC∽△A′B′C′,且相似比为3,则下列结论正确的是( )
A.AB是A′B′的3倍 B.A′B′是AB的3倍
C.∠A是∠A′的3倍 D.∠A′是∠A的3倍
4. 如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①、②、③、④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )
A.①与②相似 B.①与③相似
C.①与④相似 D.②与④相似
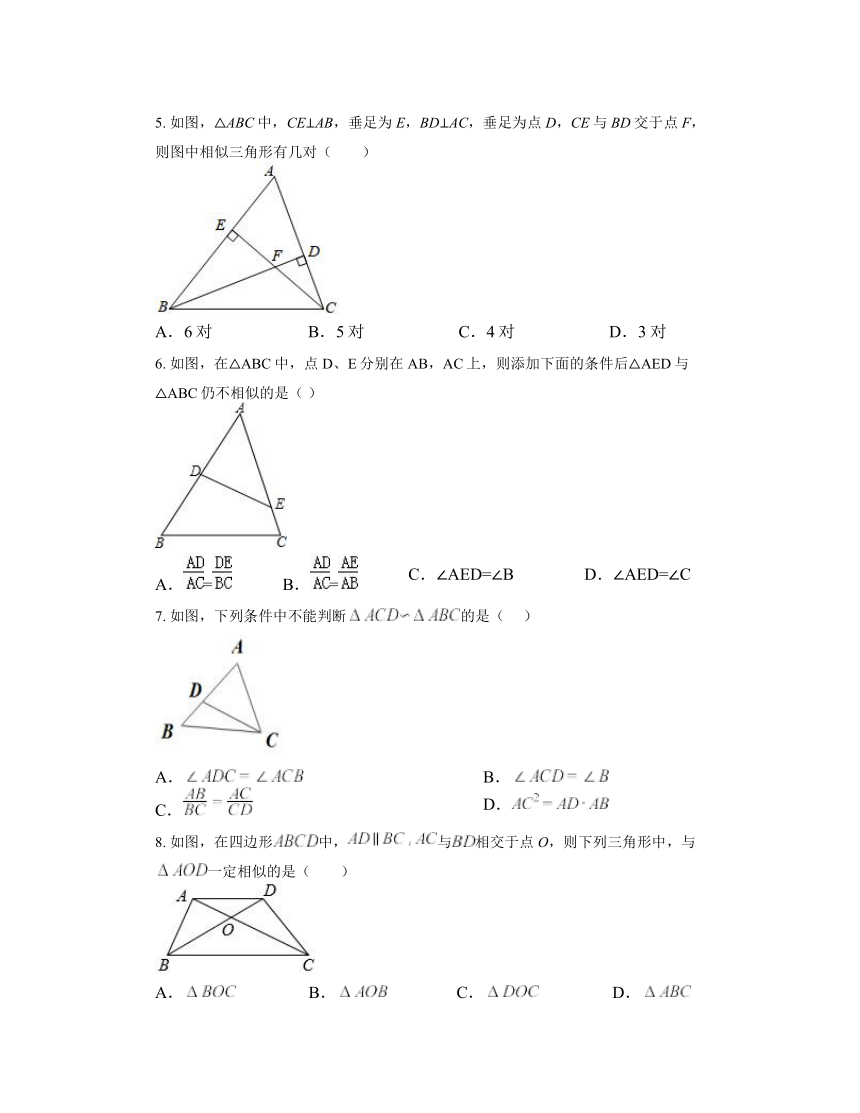
5. 如图,△ABC中,CE⊥AB,垂足为E,BD⊥AC,垂足为点D,CE与BD交于点F,则图中相似三角形有几对( )
A.6对 B.5对 C.4对 D.3对
6. 如图,在△ABC中,点D、E分别在AB,AC上,则添加下面的条件后△AED与△ABC仍不相似的是( )
A.= B.= C.∠AED=∠B D.∠AED=∠C
7. 如图,下列条件中不能判断的是( )
A. B.
C. D.
8. 如图,在四边形中,与相交于点O,则下列三角形中,与一定相似的是( )
A. B. C. D.
9. 如图,中,点D在线段上,连接,要使与相似,只需添加一个条件即可,这个条件不能是( )
A. B. C. D.
10. 如图,交于点D,,,,,则的长等于( )
A. B. C. D.
11. 如图,在锐角三角形ABC中,∠BAC=60°,BF,CE为高,点D为BC的中点,连接EF,ED,FD,有下列四个结论:①ED=FD;②∠ABC=60°时,EF∥BC;③BF=2AF;④AF:AB=AE:AC.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
12. 如图,,,,则的值为( )
A. B. C. D.
二、填空题
13. 若在△ABC内有一点D,使得∠ADB=∠ADC,AD=a,CD=b,则当BD=______时,△ABD与△ACD相似.
14. 如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=2,△ABC的面积是3,那么这个正方形的边长是_________.
15. 如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120m,DC=60m,EC=50m,求得河宽AB=______m.
16. 如图,在中,D为斜边AB上一点,AD=5,BD=4,四边形CEDF为正方形,则图中阴影部分的面积为_____________;
三、解答题
17. 如图,点B、C在线段上,且,,是边长为6的等边三角形.
求证:.
18. 如图,在平面直角坐标系xoy中,点O为坐标原点,矩形AOCD的边OC、OA分别在x轴、y轴上,点D的坐标为(6,4),点P是线段AD边上的任意一点(不含端点A、D),连结PC,过点P作PE⊥PC交AO于E点.
(1)当点P坐标为(4,4)时,求点E的坐标;
(2)当点P坐标为(5,4)时,在线段AD上是否存在不同于P的点Q,使得QC⊥QE?若存在,求出点Q的坐标;若不存在,请说明理由;
(3)当点P在AD上运动时,对应的点E也随之在AO上运动,求OE的取值范围.
19. 如图,点G是边长为4的正方形ABCD的边BC上的一点,矩形DEFG的边EF过点A,GD=5.
(1)寻找并证明图中的两组相似三角形;
(2)求HG、FG的长.
20. 如图(1),抛物线与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为(﹣2,0).
(1)求此抛物线的解析式;
(2)①若点D是第一象限内抛物线上的一个动点,过点D作DE⊥x轴于E,连接CD,以OE为直径作⊙M,如图(2),试求当CD与⊙M相切时D点的坐标;
②点F是x轴上的动点,在抛物线上是否存在一点G,使A、C、G、F四点为顶点的四边形是平行四边形?若存在,求出点G的坐标;若不存在,请说明理由.
一、选择题
1. 下列命题中正确的有( )
①有一个角等于80°的两个等腰三角形相似;
②两边对应成比例的两个等腰三角形相似;
③有一个角对应相等的两个等腰三角形相似;
④底边对应相等的两个等腰三角形相似.
A.0个 B.1个 C.2个 D.3个
2. 矩形ABCD中,点E、F分别在AD、CD上,且∠BEF=90 ,则三角形Ⅰ,Ⅱ,Ⅲ,Ⅳ一定相似的是 ( ).
A.Ⅰ和Ⅱ B.Ⅰ和Ⅲ C.Ⅰ和Ⅳ D.Ⅲ和Ⅳ
3. 已知△ABC∽△A′B′C′,且相似比为3,则下列结论正确的是( )
A.AB是A′B′的3倍 B.A′B′是AB的3倍
C.∠A是∠A′的3倍 D.∠A′是∠A的3倍
4. 如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①、②、③、④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )
A.①与②相似 B.①与③相似
C.①与④相似 D.②与④相似
5. 如图,△ABC中,CE⊥AB,垂足为E,BD⊥AC,垂足为点D,CE与BD交于点F,则图中相似三角形有几对( )
A.6对 B.5对 C.4对 D.3对
6. 如图,在△ABC中,点D、E分别在AB,AC上,则添加下面的条件后△AED与△ABC仍不相似的是( )
A.= B.= C.∠AED=∠B D.∠AED=∠C
7. 如图,下列条件中不能判断的是( )
A. B.
C. D.
8. 如图,在四边形中,与相交于点O,则下列三角形中,与一定相似的是( )
A. B. C. D.
9. 如图,中,点D在线段上,连接,要使与相似,只需添加一个条件即可,这个条件不能是( )
A. B. C. D.
10. 如图,交于点D,,,,,则的长等于( )
A. B. C. D.
11. 如图,在锐角三角形ABC中,∠BAC=60°,BF,CE为高,点D为BC的中点,连接EF,ED,FD,有下列四个结论:①ED=FD;②∠ABC=60°时,EF∥BC;③BF=2AF;④AF:AB=AE:AC.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
12. 如图,,,,则的值为( )
A. B. C. D.
二、填空题
13. 若在△ABC内有一点D,使得∠ADB=∠ADC,AD=a,CD=b,则当BD=______时,△ABD与△ACD相似.
14. 如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=2,△ABC的面积是3,那么这个正方形的边长是_________.
15. 如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120m,DC=60m,EC=50m,求得河宽AB=______m.
16. 如图,在中,D为斜边AB上一点,AD=5,BD=4,四边形CEDF为正方形,则图中阴影部分的面积为_____________;
三、解答题
17. 如图,点B、C在线段上,且,,是边长为6的等边三角形.
求证:.
18. 如图,在平面直角坐标系xoy中,点O为坐标原点,矩形AOCD的边OC、OA分别在x轴、y轴上,点D的坐标为(6,4),点P是线段AD边上的任意一点(不含端点A、D),连结PC,过点P作PE⊥PC交AO于E点.
(1)当点P坐标为(4,4)时,求点E的坐标;
(2)当点P坐标为(5,4)时,在线段AD上是否存在不同于P的点Q,使得QC⊥QE?若存在,求出点Q的坐标;若不存在,请说明理由;
(3)当点P在AD上运动时,对应的点E也随之在AO上运动,求OE的取值范围.
19. 如图,点G是边长为4的正方形ABCD的边BC上的一点,矩形DEFG的边EF过点A,GD=5.
(1)寻找并证明图中的两组相似三角形;
(2)求HG、FG的长.
20. 如图(1),抛物线与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为(﹣2,0).
(1)求此抛物线的解析式;
(2)①若点D是第一象限内抛物线上的一个动点,过点D作DE⊥x轴于E,连接CD,以OE为直径作⊙M,如图(2),试求当CD与⊙M相切时D点的坐标;
②点F是x轴上的动点,在抛物线上是否存在一点G,使A、C、G、F四点为顶点的四边形是平行四边形?若存在,求出点G的坐标;若不存在,请说明理由.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
