11.2.2三角形的外角 同步练习(无答案) 2023-2024学年人教版数学八年级上册
文档属性
| 名称 | 11.2.2三角形的外角 同步练习(无答案) 2023-2024学年人教版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 167.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 18:23:32 | ||
图片预览


文档简介
11.2.2三角形的外角 同步练习
一、单选题
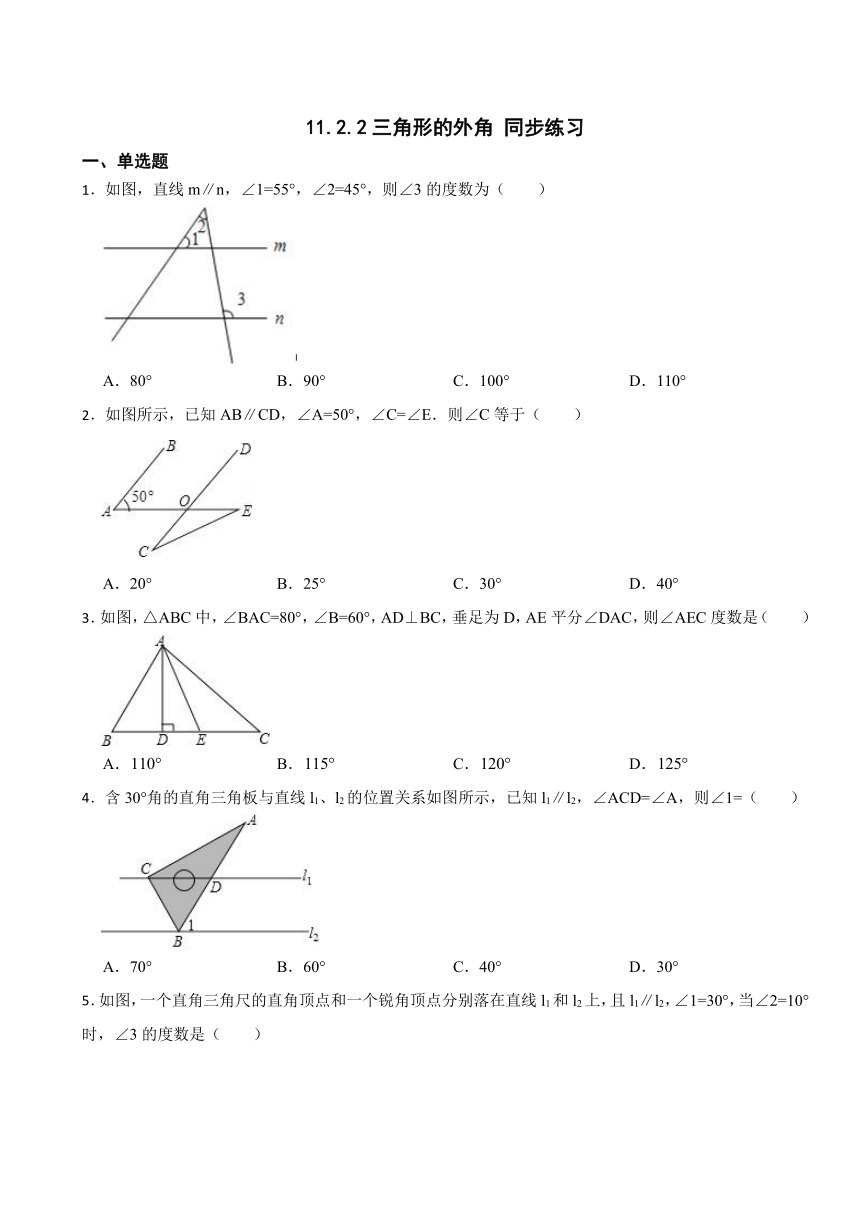
1.如图,直线m∥n,∠1=55°,∠2=45°,则∠3的度数为( )
A.80° B.90° C.100° D.110°
2.如图所示,已知AB∥CD,∠A=50°,∠C=∠E.则∠C等于( )
A.20° B.25° C.30° D.40°
3.如图,△ABC中,∠BAC=80°,∠B=60°,AD⊥BC,垂足为D,AE平分∠DAC,则∠AEC度数是( )
A. B. C. D.
4.含30°角的直角三角板与直线l1、l2的位置关系如图所示,已知l1∥l2,∠ACD=∠A,则∠1=( )
A.70° B.60° C.40° D.30°
5.如图,一个直角三角尺的直角顶点和一个锐角顶点分别落在直线l1和l2上,且l1∥l2,∠1=30°,当∠2=10°时,∠3的度数是( )
A.45° B.40° C.35° D.30°
6.如图,AD是∠CAE的平分线,∠B=35°,∠DAE=60°,则∠ACD=( )
A.25° B.85° C.60° D.95°
7.如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠BED的度数是( )
A.16° B.33° C.49° D.66°
8.如右下图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=25°,则∠2的度数为( )
A.20° B.25° C.30° D.35°
9.如图所示,D是△ABC边AC上的一点,E是BD上的一点,∠1,∠2,∠A之间的关系描述正确的是( )
A.∠A <∠1>∠2 B.∠2>∠1>∠A
C.∠1>∠2>∠A D.无法确定
10.如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点 (点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:
①α+β,②α-β,③β-α,④360°-α-β,
则∠AEC的度数可能是( )
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题
11.如图,已知∠ABE=130°,∠C=70°,则∠A= ;
12.如图,将三角尺的直角顶点放在直尺的一边上, , ,则 的度数为 .
13.如图,直线a,b被直线c所截,若a∥b,∠1=110°,∠2=40°,则∠3= °.
14.“三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图所示的“三等分角仪”能三等分任何一个角.这个三等分角仪由两很有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D, E可在槽中滑动,若∠BDE=78°,则∠AOB等于 度.
15.如图,已知,,点E、F在线段上,且满足平分,平分,可以左右平行移动.给出下列四个结论.其中正确的结论有 (填写所有正确结论的序号).
①;
②;
③;
④
三、解答题
16.已知:如图,在△ABC中,∠B=∠C,AD平分外角∠EAC.
求证:AD∥BC.
17.一个零件的形状如图所示,按规定∠A=90 ,∠C=25 ,∠B=25 ,检验员已量得∠BDC=150 ,请问:这个零件合格吗?说明理由。
18.已知:如图,∠CAE是△ABC的外角,AD∥BC且∠1=∠2,求证:AB=AC.
19.如图,AD是△ABC的高,BE平分∠ABC交AD于E,若∠C=70°,∠BED=64°,求∠BAC的度数.
20.如图,已知:平分,点F是反向延长线上的一点,,.求:和的度数.
21.如图,在直角坐标系中,点A、B分别在射线OX、OY上移动,BE是∠ABY的角平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明.
一、单选题
1.如图,直线m∥n,∠1=55°,∠2=45°,则∠3的度数为( )
A.80° B.90° C.100° D.110°
2.如图所示,已知AB∥CD,∠A=50°,∠C=∠E.则∠C等于( )
A.20° B.25° C.30° D.40°
3.如图,△ABC中,∠BAC=80°,∠B=60°,AD⊥BC,垂足为D,AE平分∠DAC,则∠AEC度数是( )
A. B. C. D.
4.含30°角的直角三角板与直线l1、l2的位置关系如图所示,已知l1∥l2,∠ACD=∠A,则∠1=( )
A.70° B.60° C.40° D.30°
5.如图,一个直角三角尺的直角顶点和一个锐角顶点分别落在直线l1和l2上,且l1∥l2,∠1=30°,当∠2=10°时,∠3的度数是( )
A.45° B.40° C.35° D.30°
6.如图,AD是∠CAE的平分线,∠B=35°,∠DAE=60°,则∠ACD=( )
A.25° B.85° C.60° D.95°
7.如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠BED的度数是( )
A.16° B.33° C.49° D.66°
8.如右下图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=25°,则∠2的度数为( )
A.20° B.25° C.30° D.35°
9.如图所示,D是△ABC边AC上的一点,E是BD上的一点,∠1,∠2,∠A之间的关系描述正确的是( )
A.∠A <∠1>∠2 B.∠2>∠1>∠A
C.∠1>∠2>∠A D.无法确定
10.如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点 (点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:
①α+β,②α-β,③β-α,④360°-α-β,
则∠AEC的度数可能是( )
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题
11.如图,已知∠ABE=130°,∠C=70°,则∠A= ;
12.如图,将三角尺的直角顶点放在直尺的一边上, , ,则 的度数为 .
13.如图,直线a,b被直线c所截,若a∥b,∠1=110°,∠2=40°,则∠3= °.
14.“三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图所示的“三等分角仪”能三等分任何一个角.这个三等分角仪由两很有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D, E可在槽中滑动,若∠BDE=78°,则∠AOB等于 度.
15.如图,已知,,点E、F在线段上,且满足平分,平分,可以左右平行移动.给出下列四个结论.其中正确的结论有 (填写所有正确结论的序号).
①;
②;
③;
④
三、解答题
16.已知:如图,在△ABC中,∠B=∠C,AD平分外角∠EAC.
求证:AD∥BC.
17.一个零件的形状如图所示,按规定∠A=90 ,∠C=25 ,∠B=25 ,检验员已量得∠BDC=150 ,请问:这个零件合格吗?说明理由。
18.已知:如图,∠CAE是△ABC的外角,AD∥BC且∠1=∠2,求证:AB=AC.
19.如图,AD是△ABC的高,BE平分∠ABC交AD于E,若∠C=70°,∠BED=64°,求∠BAC的度数.
20.如图,已知:平分,点F是反向延长线上的一点,,.求:和的度数.
21.如图,在直角坐标系中,点A、B分别在射线OX、OY上移动,BE是∠ABY的角平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明.
