11.3多边形及其内角和 同步练习(含答案)2023—2024学年人教版数学八年级上册
文档属性
| 名称 | 11.3多边形及其内角和 同步练习(含答案)2023—2024学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 142.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 18:43:07 | ||
图片预览

文档简介
11.3多边形及其内角和
一、选择题
1.如果一个多边形从一个顶点出发最多能画三条对角线,则这个多边形的边数为( )
A.4 B.5 C.6 D.7
2. 一个多边形对角线的条数是边数的3倍,则这个多边形是( )
A.七边形 B.八边形 C.九边形 D.十边形
3.一个多边形内角和是900°,则这个多边形是( )
A.六边形 B.七边形 C.八边形 D.九边形
4.n边形所有对角线的条数有( )
A. 条 B. 条 C. 条 D. 条
5.十边形的内角和是外角和的( )倍.
A.3 B.4 C.5 D.6
6.若一个多边形的内角和为 540°,那么这个多边形对角线的条数为( )
A.5 B.6 C.7 D.8
7.如图,已知,那么的度数为( )
A. B. C. D.
8.在学习多边形的内角和外角知识以后,2班的小朋友们在操场做了一个实验,如图,张梓佑从点出发沿直线前进8米到达点后向左旋转度,再沿直线前进8米,到达点后,又向左旋转度,照这样走下去,第一次回到出发地点时,她共走了72米,请计算出张梓佑每次旋转的角度为( )
A. B. C. D.
二、填空题
9.如果过某多边形的一个顶点的对角线有6条,则该多边形一共有 条对角线.
10.正多边形的一个内角是108°,则这个多边形的边数是 .
11.过多边形某个顶点的所有对角线,将这个多边形分成7个三角形,这个多边形是 .
12.一个多边形的内角和与它的外角和之比为,则这个多边形的边数是 .
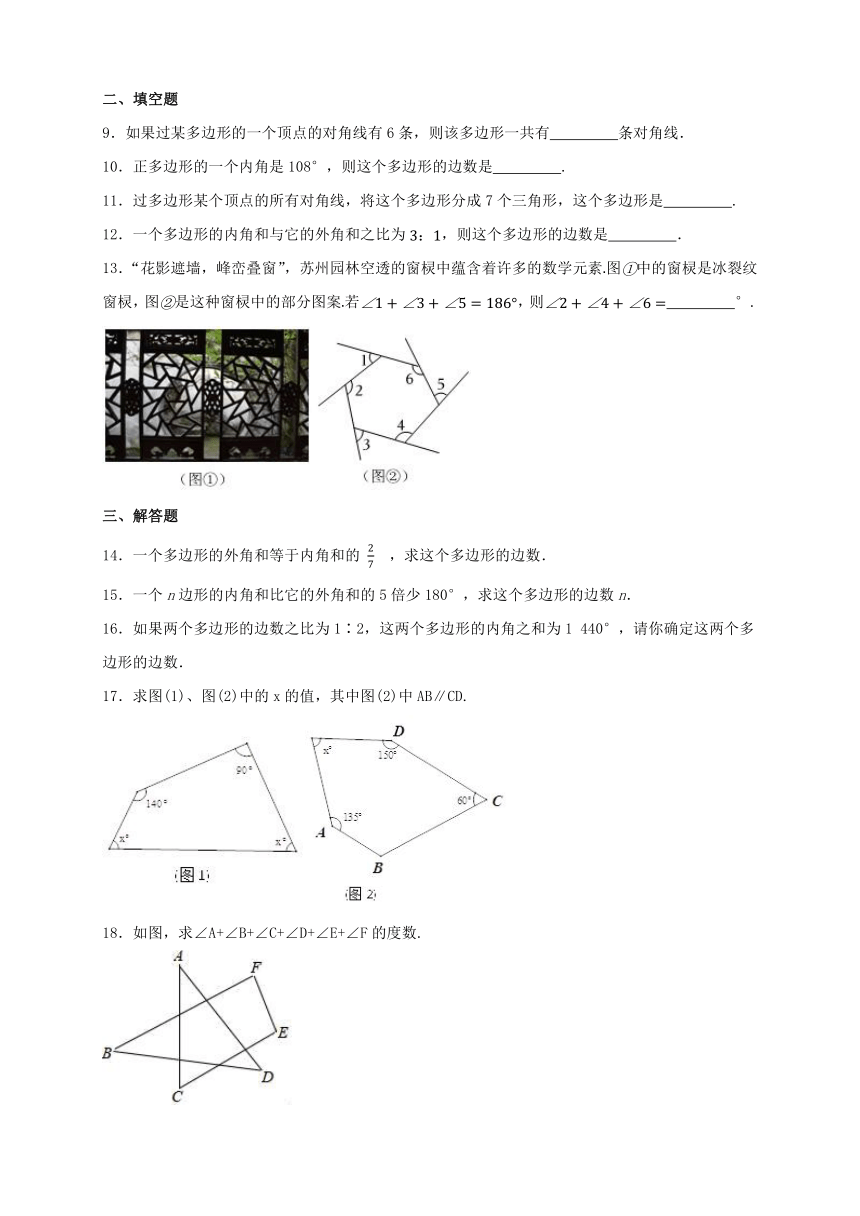
13.“花影遮墙,峰峦叠窗”,苏州园林空透的窗棂中蕴含着许多的数学元素图中的窗棂是冰裂纹窗棂,图是这种窗棂中的部分图案若,则 °.
三、解答题
14.一个多边形的外角和等于内角和的 ,求这个多边形的边数.
15.一个n边形的内角和比它的外角和的5倍少180°,求这个多边形的边数n.
16.如果两个多边形的边数之比为1∶2,这两个多边形的内角之和为1 440°,请你确定这两个多边形的边数.
17.求图(1)、图(2)中的x的值,其中图(2)中AB∥CD.
18.如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
参考答案
1.C
2.C
3.D
4.C
5.B
6.A
7.D
8.B
9.27
10.5
11.
12.8
13.366
14.解:设这个多边形的边数为n,则
(n-2)·180= 360
解之得 n=9
答:这个多边形的边数是9.
15.解:由题意得:(n-3)×180°=360°×5-180°,
∴n-3=9,
∴n=12.
16.解:设边数较少的多边形的边数为n,则 (n-2)·180+(2n-2)·180=1 440. 解得n=4,2n=8. 答:这两个多边形的边数分别为4,8.
17.解:(1)根据题意得,x°+x°+140°+90°=360°,
解得,x=65;
( 2 )∵AB∥CD,
∴∠B+∠C=180°,
∵∠C=60°,
∴∠B=120°,
∴x°+135°+120°+60°+150°=(5-2)×180°,
解得,x=75.
18.解:连接BC,
∵在△BOC和△AOD中,∠1=∠2,
∴∠A+∠D=∠DBC+∠ACB,
∴∠A+∠B+∠C+∠D+∠E+∠F=∠DBC+∠ACB+∠DBF+∠ACE+∠E+∠F=∠FBC+∠BCE+∠E+∠F=360°
一、选择题
1.如果一个多边形从一个顶点出发最多能画三条对角线,则这个多边形的边数为( )
A.4 B.5 C.6 D.7
2. 一个多边形对角线的条数是边数的3倍,则这个多边形是( )
A.七边形 B.八边形 C.九边形 D.十边形
3.一个多边形内角和是900°,则这个多边形是( )
A.六边形 B.七边形 C.八边形 D.九边形
4.n边形所有对角线的条数有( )
A. 条 B. 条 C. 条 D. 条
5.十边形的内角和是外角和的( )倍.
A.3 B.4 C.5 D.6
6.若一个多边形的内角和为 540°,那么这个多边形对角线的条数为( )
A.5 B.6 C.7 D.8
7.如图,已知,那么的度数为( )
A. B. C. D.
8.在学习多边形的内角和外角知识以后,2班的小朋友们在操场做了一个实验,如图,张梓佑从点出发沿直线前进8米到达点后向左旋转度,再沿直线前进8米,到达点后,又向左旋转度,照这样走下去,第一次回到出发地点时,她共走了72米,请计算出张梓佑每次旋转的角度为( )
A. B. C. D.
二、填空题
9.如果过某多边形的一个顶点的对角线有6条,则该多边形一共有 条对角线.
10.正多边形的一个内角是108°,则这个多边形的边数是 .
11.过多边形某个顶点的所有对角线,将这个多边形分成7个三角形,这个多边形是 .
12.一个多边形的内角和与它的外角和之比为,则这个多边形的边数是 .
13.“花影遮墙,峰峦叠窗”,苏州园林空透的窗棂中蕴含着许多的数学元素图中的窗棂是冰裂纹窗棂,图是这种窗棂中的部分图案若,则 °.
三、解答题
14.一个多边形的外角和等于内角和的 ,求这个多边形的边数.
15.一个n边形的内角和比它的外角和的5倍少180°,求这个多边形的边数n.
16.如果两个多边形的边数之比为1∶2,这两个多边形的内角之和为1 440°,请你确定这两个多边形的边数.
17.求图(1)、图(2)中的x的值,其中图(2)中AB∥CD.
18.如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
参考答案
1.C
2.C
3.D
4.C
5.B
6.A
7.D
8.B
9.27
10.5
11.
12.8
13.366
14.解:设这个多边形的边数为n,则
(n-2)·180= 360
解之得 n=9
答:这个多边形的边数是9.
15.解:由题意得:(n-3)×180°=360°×5-180°,
∴n-3=9,
∴n=12.
16.解:设边数较少的多边形的边数为n,则 (n-2)·180+(2n-2)·180=1 440. 解得n=4,2n=8. 答:这两个多边形的边数分别为4,8.
17.解:(1)根据题意得,x°+x°+140°+90°=360°,
解得,x=65;
( 2 )∵AB∥CD,
∴∠B+∠C=180°,
∵∠C=60°,
∴∠B=120°,
∴x°+135°+120°+60°+150°=(5-2)×180°,
解得,x=75.
18.解:连接BC,
∵在△BOC和△AOD中,∠1=∠2,
∴∠A+∠D=∠DBC+∠ACB,
∴∠A+∠B+∠C+∠D+∠E+∠F=∠DBC+∠ACB+∠DBF+∠ACE+∠E+∠F=∠FBC+∠BCE+∠E+∠F=360°
