13.3.1 等腰三角形练习(无答案)2023—2024学年人教版数学八年级上册
文档属性
| 名称 | 13.3.1 等腰三角形练习(无答案)2023—2024学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 193.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 00:00:00 | ||
图片预览

文档简介
等腰三角形
一、单选题
1.等腰三角形具有“三线合一”的性质,以下哪个不是三线之一( )
A.底边上的高 B.腰上的高 C.底边上的中线 D.顶角的角平分线
2.等腰三角形有一个角是,则它的底角是( )
A. B. C. D.
3.在平面直角坐标系xOy中,已知点,在y轴上确定点P,使为等腰三角形,则符合条件的有( )个.
A.5 B.4 C.3 D.2
4.等腰三角形有一个外角是110°,则其顶角度数是( )
A.70° B.70°或40° C.40° D.110°或40°
5.已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB,AC于点D,E,若DE=8,则线段BD+CE的长为( )
A.5 B.6 C.7 D.8
6.如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=70°,则∠BAC的大小为( )
A.40° B.30° C.70° D.50°
7.如图,中,垂直平分,点P为直线上的任一点,则周长的最小值是( )
A.10 B.14 C.15 D.19
二、填空题
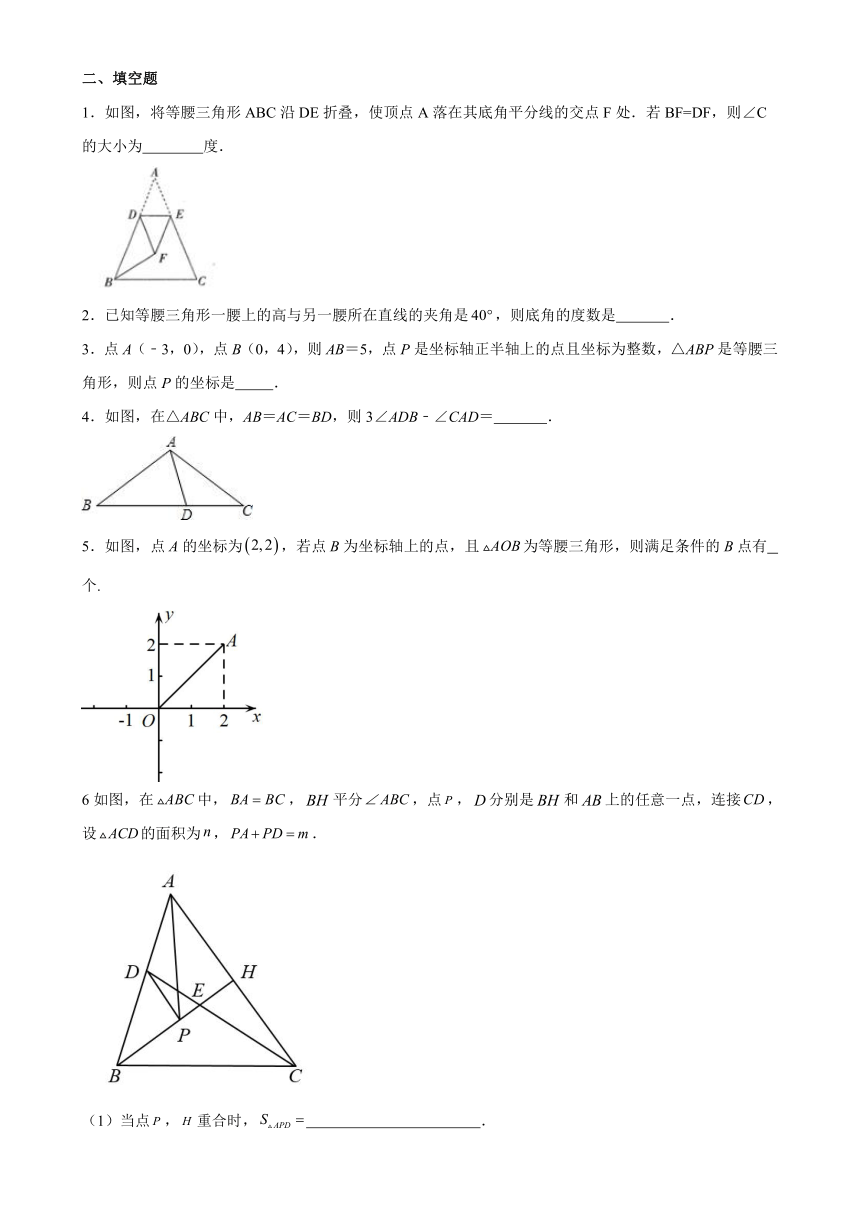
1.如图,将等腰三角形ABC沿DE折叠,使顶点A落在其底角平分线的交点F处.若BF=DF,则∠C的大小为 度.
2.已知等腰三角形一腰上的高与另一腰所在直线的夹角是,则底角的度数是 .
3.点A(﹣3,0),点B(0,4),则AB=5,点P是坐标轴正半轴上的点且坐标为整数,△ABP是等腰三角形,则点P的坐标是 .
4.如图,在△ABC中,AB=AC=BD,则3∠ADB﹣∠CAD= .
5.如图,点A的坐标为,若点B为坐标轴上的点,且为等腰三角形,则满足条件的B点有 个.
6如图,在中,,平分,点,分别是和上的任意一点,连接,设的面积为,.
(1)当点,重合时, .
(2)连接交于点,则 (填“”,“”,“”,“”或“”);
三、解答题
1.如图,在△ABC中,CD=CA,CE⊥AD于点E,BF⊥AD于点F.求证:∠ACE=∠DBF.
2.在 中, ,点 , 分别在 、 上, , 与 相交于点 .求证: ,并请直接写出图中其他所有相等的线段.
3.如图,已知D是∠ABC的平分线与△ABC的外角平分线的交点,DE∥BC,交AB于点E,交AC于点F.
求证:EF=BE-CF
4.如图,在 中, , 于D,E是 上的一点, 交 的延长线于F.求证: .
5.在八年级上册“轴对称图形”一章69页中我们曾做过“折纸与证明”的数学活动:折纸,常常能为证明一个命题提供思路和方法.请用你所学知识解决下列问题.
将()沿折叠,使点C刚好落在边上的点E处.
(1)图1中,,则___________;___________;
(2)如图2,若,试说明:.
一、单选题
1.等腰三角形具有“三线合一”的性质,以下哪个不是三线之一( )
A.底边上的高 B.腰上的高 C.底边上的中线 D.顶角的角平分线
2.等腰三角形有一个角是,则它的底角是( )
A. B. C. D.
3.在平面直角坐标系xOy中,已知点,在y轴上确定点P,使为等腰三角形,则符合条件的有( )个.
A.5 B.4 C.3 D.2
4.等腰三角形有一个外角是110°,则其顶角度数是( )
A.70° B.70°或40° C.40° D.110°或40°
5.已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB,AC于点D,E,若DE=8,则线段BD+CE的长为( )
A.5 B.6 C.7 D.8
6.如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=70°,则∠BAC的大小为( )
A.40° B.30° C.70° D.50°
7.如图,中,垂直平分,点P为直线上的任一点,则周长的最小值是( )
A.10 B.14 C.15 D.19
二、填空题
1.如图,将等腰三角形ABC沿DE折叠,使顶点A落在其底角平分线的交点F处.若BF=DF,则∠C的大小为 度.
2.已知等腰三角形一腰上的高与另一腰所在直线的夹角是,则底角的度数是 .
3.点A(﹣3,0),点B(0,4),则AB=5,点P是坐标轴正半轴上的点且坐标为整数,△ABP是等腰三角形,则点P的坐标是 .
4.如图,在△ABC中,AB=AC=BD,则3∠ADB﹣∠CAD= .
5.如图,点A的坐标为,若点B为坐标轴上的点,且为等腰三角形,则满足条件的B点有 个.
6如图,在中,,平分,点,分别是和上的任意一点,连接,设的面积为,.
(1)当点,重合时, .
(2)连接交于点,则 (填“”,“”,“”,“”或“”);
三、解答题
1.如图,在△ABC中,CD=CA,CE⊥AD于点E,BF⊥AD于点F.求证:∠ACE=∠DBF.
2.在 中, ,点 , 分别在 、 上, , 与 相交于点 .求证: ,并请直接写出图中其他所有相等的线段.
3.如图,已知D是∠ABC的平分线与△ABC的外角平分线的交点,DE∥BC,交AB于点E,交AC于点F.
求证:EF=BE-CF
4.如图,在 中, , 于D,E是 上的一点, 交 的延长线于F.求证: .
5.在八年级上册“轴对称图形”一章69页中我们曾做过“折纸与证明”的数学活动:折纸,常常能为证明一个命题提供思路和方法.请用你所学知识解决下列问题.
将()沿折叠,使点C刚好落在边上的点E处.
(1)图1中,,则___________;___________;
(2)如图2,若,试说明:.
