13.4 课题学习 最短路径问题 导学案(含答案)2023—2024学年人教版数学 八年级上册
文档属性
| 名称 | 13.4 课题学习 最短路径问题 导学案(含答案)2023—2024学年人教版数学 八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 955.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 19:31:27 | ||
图片预览


文档简介
13.4 课题学习 最短路径问题
人教版数学 八年级上册
1.最短路径问题解题根据:
(1)两点的所有连线中,段线最短.
(2)连接直线外一点与直线上各点的所有线段中,垂线段最短.
2.最短路径问题类型:
(1)在直线上找一点,使这个点到直最短路径问题线异侧的两个点的距离(PA+PB)最短。
如图所示,连接AB,与直线相交于一点P,根据“两点之间线段最短",可知P点就是要找的点.
(2)在直线上找一点,使这个点到直线同侧的两个点的距离的和(PA+PB)最小.
如图所示.在直线旁作以直线为对称轴的A点的对称点A',再将这一对称点A'与另一点B连接交直线于P点,这个点P即为所求的点。
(3)在直线1、2上分别求点M、N,使△PMN的周长最小.
如图所示,分别作点P关于两直线1、2的对称点P',P",连接P'P",与两直线的交点即为点M,N。△PMN周长的最小值为线段P'P"的值。
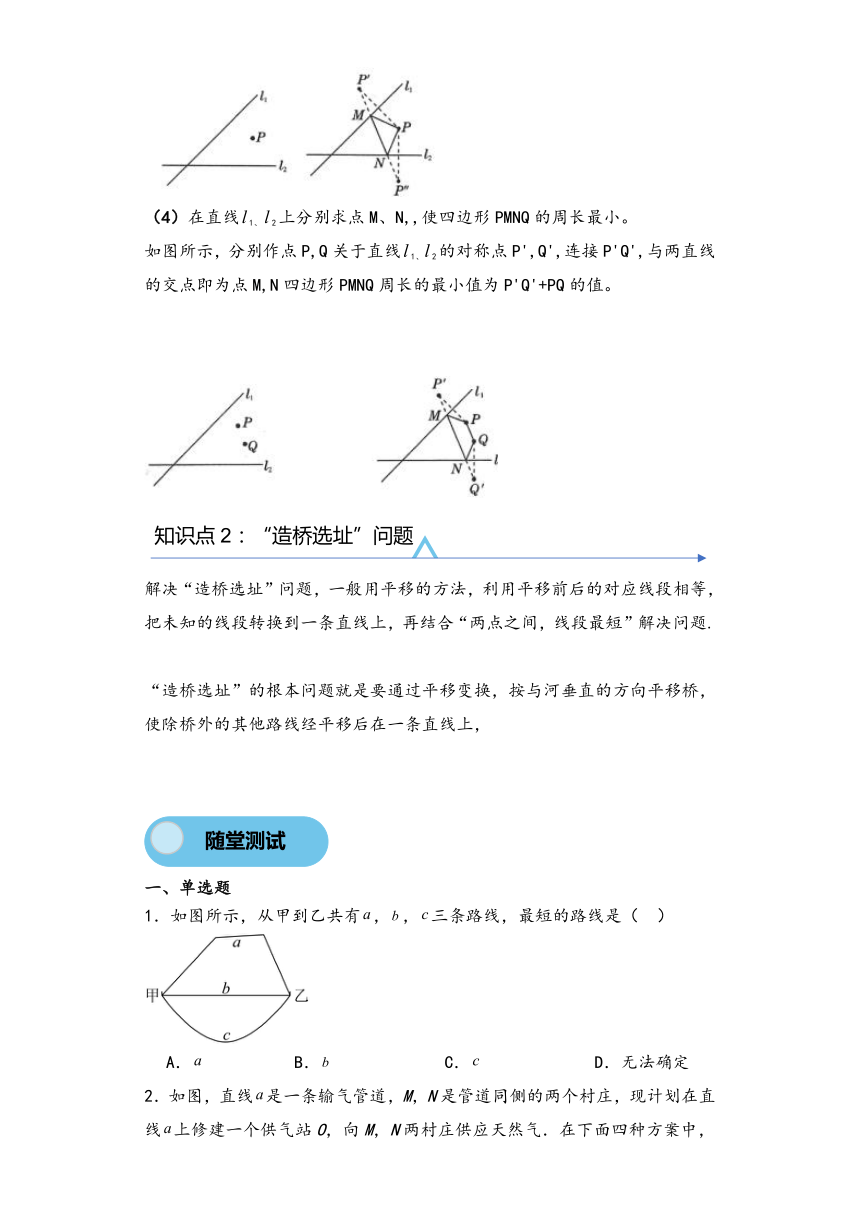
(4)在直线1、2上分别求点M、N,,使四边形PMNQ的周长最小。
如图所示,分别作点P,Q关于直线1、2的对称点P',Q',连接P'Q',与两直线的交点即为点M,N四边形PMNQ周长的最小值为P'Q'+PQ的值。
解决“造桥选址”问题,一般用平移的方法,利用平移前后的对应线段相等,把未知的线段转换到一条直线上,再结合“两点之间,线段最短”解决问题.
“造桥选址”的根本问题就是要通过平移变换,按与河垂直的方向平移桥,使除桥外的其他路线经平移后在一条直线上,
一、单选题
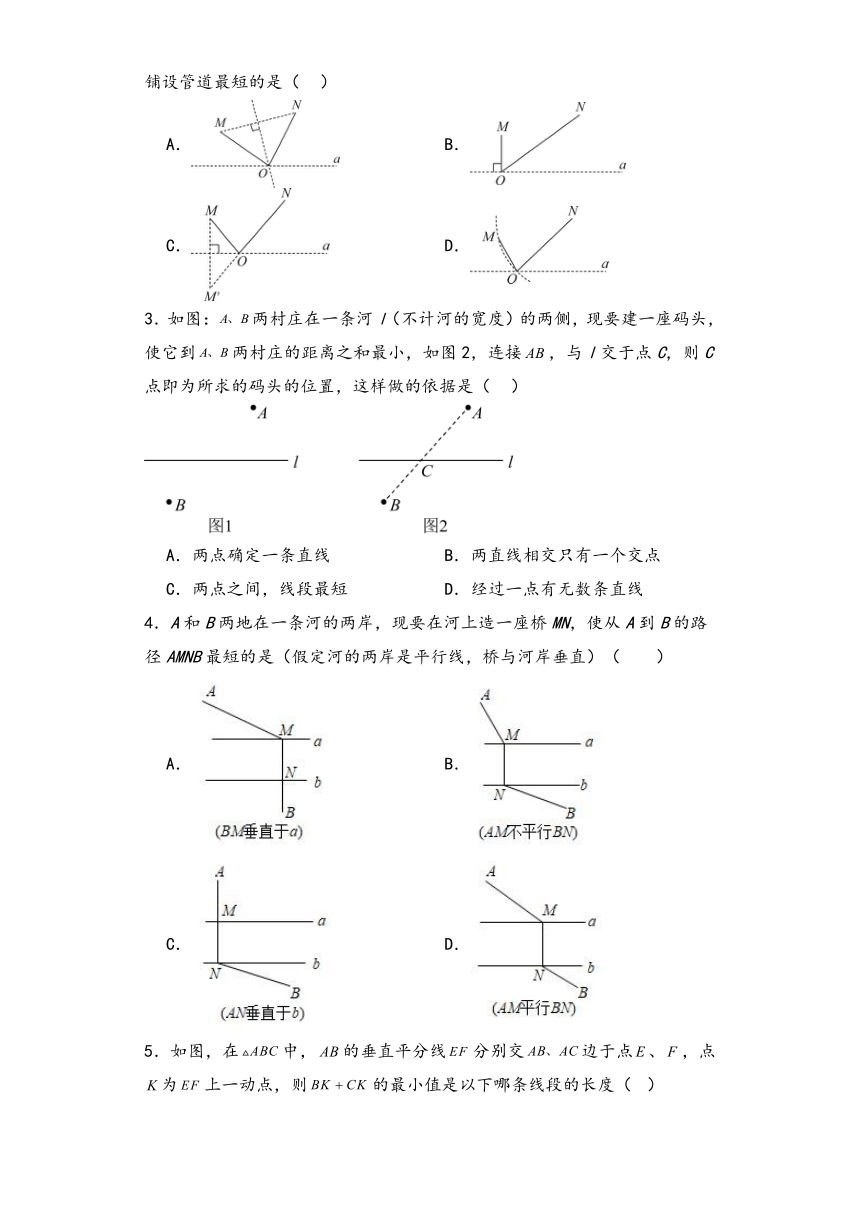
1.如图所示,从甲到乙共有,,三条路线,最短的路线是( )
A. B. C. D.无法确定
2.如图,直线是一条输气管道,M,N是管道同侧的两个村庄,现计划在直线上修建一个供气站O,向M,N两村庄供应天然气.在下面四种方案中,铺设管道最短的是( )
A. B.
C. D.
3.如图:两村庄在一条河l(不计河的宽度)的两侧,现要建一座码头,使它到两村庄的距离之和最小,如图2,连接,与l交于点C,则C点即为所求的码头的位置,这样做的依据是( )
A.两点确定一条直线 B.两直线相交只有一个交点
C.两点之间,线段最短 D.经过一点有无数条直线
4.A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行线,桥与河岸垂直)( )
A. B.
C. D.
5.如图,在中,的垂直平分线分别交边于点、,点为上一动点,则的最小值是以下哪条线段的长度( )
A. B. C. D.
6.如图,从地到地的最短路线是( )
A. B.
C. D.
7.如图,边长为的等边中,是上中线且,点在上,连接,在的右侧作等边,连接,则周长的最小值是( )
A. B. C. D.
8.如图,在中,AB=AC=7,AD=8.3,点E在AD上,CE=CB,CF平分∠BCE交AD于点F.点P是线段CF上一动点,则EP+AP的最小值为( )
A.6 B.7 C.7.5 D.8.3
二、填空题
9.如图,已知空间站与星球距离为,信号飞船在星球附近沿圆形轨道行驶,,之间的距离为数据表示飞船与空间站的实时距离,那么的最小值 .
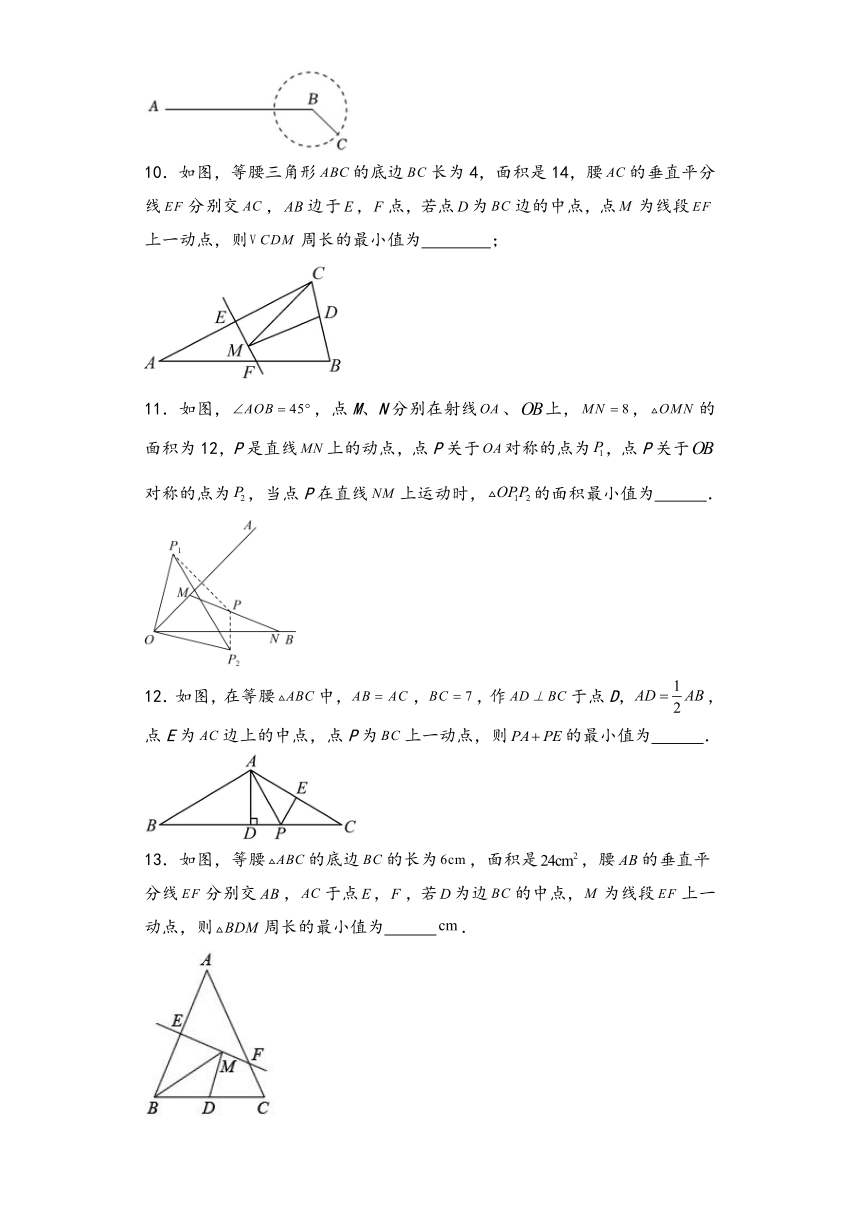
10.如图,等腰三角形的底边长为4,面积是14,腰的垂直平分线分别交,边于,点,若点为边的中点,点为线段上一动点,则周长的最小值为 ;
11.如图,,点M、N分别在射线、上,,的面积为12,P是直线上的动点,点P关于对称的点为,点P关于对称的点为,当点P在直线上运动时,的面积最小值为 .
12.如图,在等腰中,,,作于点D,,点E为边上的中点,点P为上一动点,则的最小值为 .
13.如图,等腰的底边的长为,面积是,腰的垂直平分线分别交,于点,,若为边的中点,为线段上一动点,则周长的最小值为 .
三、解答题
14.如图,在正方形网格中,点A、B、C、M、N都在格点上.
(1)作关于直线对称的图形;
(2)点P在直线上,当周长最小时,仅用无刻度的直尺在直线上作出点P的位置.
15.如图.
(1)在网格中画出关于轴对称的.
(2)写出关于轴对称的的各顶点坐标.
(3)在轴上确定一点,使最短.(只需作图保留作图痕迹)
16.如图,在四边形中,,,,分别是,上的点,当的周长最小时,求的度数.
17.如图,已知≌,将沿所在的直线折叠至的位置,点B的对应点为,连结.
(1)直接填空:与的位置关系是__________;
(2)点P、Q分别是线段、上的两个动点(不与点A、B、C重合),已知的面积为36,,求的最小值;
(3)试探索:的内角满足什么条件时,是直角三角形?
参考答案:
1.B
2.C
3.C
4.D
5.C
6.A
7.B
8.B
9./
10.9
11.
12.
13.11
14.(1)见解析
(2)见解析
【详解】(1)解:如图,即为所求;
(2)∵点关于的对称点为,连接交直线于点,
此时周长最小.
点即为所求.
15.(1)作图见详解
(2),,
(3)作图见详解
【详解】(1)解:根据题意得,,,,
∵点关于轴对称的点的特点是横坐标变为原来的相反数,纵坐标不变,
∴,,,如图所示,连接,
∴即为所求图形.
(2)解:由(1)可知,,,,
∵点关于轴对称的点的特点是横坐标不变,纵坐标变为原来的相反数,
∴,,.
(3)解:如图所示,作点关于轴对称的点,连接,则与轴交于点,
∴根据对称可得,,
∴,
∵点两点之间线段最短,
∴最短,即的值最小,
∴如图所示,点的位置即为所求点的位置.
16.
【详解】解:如答图①,分别作点关于直线,的对称点,,
则,.
的周长,
当,,,四点共线(如答图②)时,的周长取到最小值.
,,
.
根据轴对称的性质可得,.
又由三角形的一个外角等于和它不相邻的两个内角和,可得,
又
,
,
,
,
.
17.(1)
(2)9
(3)当时,;当时,
【详解】(1)解:∵沿所在的直线折叠至的位置,点B的对应点为,
∴,
故答案为:;
(2)解:如图所示,在上取点,使得,连接,
根据对称的性质,,
∴,
要求的最小值,求的最小值即可,
∴当B、P、M三点共线,且时,取得最小值,
此时,如图所示,
由对称的性质,,
∵取得最小值时,,
∴,
即:,解得:,
∴的最小值为9;
(3)解:①当时,;
∵由翻折变换的性质可知,,
∴,
∵,
∴,
∴,
∴;
②由翻折的性质,当时,.
形状和大小不变,位置变化,对应边和对应角相等是解题关键.
人教版数学 八年级上册
1.最短路径问题解题根据:
(1)两点的所有连线中,段线最短.
(2)连接直线外一点与直线上各点的所有线段中,垂线段最短.
2.最短路径问题类型:
(1)在直线上找一点,使这个点到直最短路径问题线异侧的两个点的距离(PA+PB)最短。
如图所示,连接AB,与直线相交于一点P,根据“两点之间线段最短",可知P点就是要找的点.
(2)在直线上找一点,使这个点到直线同侧的两个点的距离的和(PA+PB)最小.
如图所示.在直线旁作以直线为对称轴的A点的对称点A',再将这一对称点A'与另一点B连接交直线于P点,这个点P即为所求的点。
(3)在直线1、2上分别求点M、N,使△PMN的周长最小.
如图所示,分别作点P关于两直线1、2的对称点P',P",连接P'P",与两直线的交点即为点M,N。△PMN周长的最小值为线段P'P"的值。
(4)在直线1、2上分别求点M、N,,使四边形PMNQ的周长最小。
如图所示,分别作点P,Q关于直线1、2的对称点P',Q',连接P'Q',与两直线的交点即为点M,N四边形PMNQ周长的最小值为P'Q'+PQ的值。
解决“造桥选址”问题,一般用平移的方法,利用平移前后的对应线段相等,把未知的线段转换到一条直线上,再结合“两点之间,线段最短”解决问题.
“造桥选址”的根本问题就是要通过平移变换,按与河垂直的方向平移桥,使除桥外的其他路线经平移后在一条直线上,
一、单选题
1.如图所示,从甲到乙共有,,三条路线,最短的路线是( )
A. B. C. D.无法确定
2.如图,直线是一条输气管道,M,N是管道同侧的两个村庄,现计划在直线上修建一个供气站O,向M,N两村庄供应天然气.在下面四种方案中,铺设管道最短的是( )
A. B.
C. D.
3.如图:两村庄在一条河l(不计河的宽度)的两侧,现要建一座码头,使它到两村庄的距离之和最小,如图2,连接,与l交于点C,则C点即为所求的码头的位置,这样做的依据是( )
A.两点确定一条直线 B.两直线相交只有一个交点
C.两点之间,线段最短 D.经过一点有无数条直线
4.A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行线,桥与河岸垂直)( )
A. B.
C. D.
5.如图,在中,的垂直平分线分别交边于点、,点为上一动点,则的最小值是以下哪条线段的长度( )
A. B. C. D.
6.如图,从地到地的最短路线是( )
A. B.
C. D.
7.如图,边长为的等边中,是上中线且,点在上,连接,在的右侧作等边,连接,则周长的最小值是( )
A. B. C. D.
8.如图,在中,AB=AC=7,AD=8.3,点E在AD上,CE=CB,CF平分∠BCE交AD于点F.点P是线段CF上一动点,则EP+AP的最小值为( )
A.6 B.7 C.7.5 D.8.3
二、填空题
9.如图,已知空间站与星球距离为,信号飞船在星球附近沿圆形轨道行驶,,之间的距离为数据表示飞船与空间站的实时距离,那么的最小值 .
10.如图,等腰三角形的底边长为4,面积是14,腰的垂直平分线分别交,边于,点,若点为边的中点,点为线段上一动点,则周长的最小值为 ;
11.如图,,点M、N分别在射线、上,,的面积为12,P是直线上的动点,点P关于对称的点为,点P关于对称的点为,当点P在直线上运动时,的面积最小值为 .
12.如图,在等腰中,,,作于点D,,点E为边上的中点,点P为上一动点,则的最小值为 .
13.如图,等腰的底边的长为,面积是,腰的垂直平分线分别交,于点,,若为边的中点,为线段上一动点,则周长的最小值为 .
三、解答题
14.如图,在正方形网格中,点A、B、C、M、N都在格点上.
(1)作关于直线对称的图形;
(2)点P在直线上,当周长最小时,仅用无刻度的直尺在直线上作出点P的位置.
15.如图.
(1)在网格中画出关于轴对称的.
(2)写出关于轴对称的的各顶点坐标.
(3)在轴上确定一点,使最短.(只需作图保留作图痕迹)
16.如图,在四边形中,,,,分别是,上的点,当的周长最小时,求的度数.
17.如图,已知≌,将沿所在的直线折叠至的位置,点B的对应点为,连结.
(1)直接填空:与的位置关系是__________;
(2)点P、Q分别是线段、上的两个动点(不与点A、B、C重合),已知的面积为36,,求的最小值;
(3)试探索:的内角满足什么条件时,是直角三角形?
参考答案:
1.B
2.C
3.C
4.D
5.C
6.A
7.B
8.B
9./
10.9
11.
12.
13.11
14.(1)见解析
(2)见解析
【详解】(1)解:如图,即为所求;
(2)∵点关于的对称点为,连接交直线于点,
此时周长最小.
点即为所求.
15.(1)作图见详解
(2),,
(3)作图见详解
【详解】(1)解:根据题意得,,,,
∵点关于轴对称的点的特点是横坐标变为原来的相反数,纵坐标不变,
∴,,,如图所示,连接,
∴即为所求图形.
(2)解:由(1)可知,,,,
∵点关于轴对称的点的特点是横坐标不变,纵坐标变为原来的相反数,
∴,,.
(3)解:如图所示,作点关于轴对称的点,连接,则与轴交于点,
∴根据对称可得,,
∴,
∵点两点之间线段最短,
∴最短,即的值最小,
∴如图所示,点的位置即为所求点的位置.
16.
【详解】解:如答图①,分别作点关于直线,的对称点,,
则,.
的周长,
当,,,四点共线(如答图②)时,的周长取到最小值.
,,
.
根据轴对称的性质可得,.
又由三角形的一个外角等于和它不相邻的两个内角和,可得,
又
,
,
,
,
.
17.(1)
(2)9
(3)当时,;当时,
【详解】(1)解:∵沿所在的直线折叠至的位置,点B的对应点为,
∴,
故答案为:;
(2)解:如图所示,在上取点,使得,连接,
根据对称的性质,,
∴,
要求的最小值,求的最小值即可,
∴当B、P、M三点共线,且时,取得最小值,
此时,如图所示,
由对称的性质,,
∵取得最小值时,,
∴,
即:,解得:,
∴的最小值为9;
(3)解:①当时,;
∵由翻折变换的性质可知,,
∴,
∵,
∴,
∴,
∴;
②由翻折的性质,当时,.
形状和大小不变,位置变化,对应边和对应角相等是解题关键.
