第1章 三角形 单元测试卷(含解析)2023—2024学年鲁教版(五四制)数学七年级上册
文档属性
| 名称 | 第1章 三角形 单元测试卷(含解析)2023—2024学年鲁教版(五四制)数学七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 102.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 19:33:59 | ||
图片预览



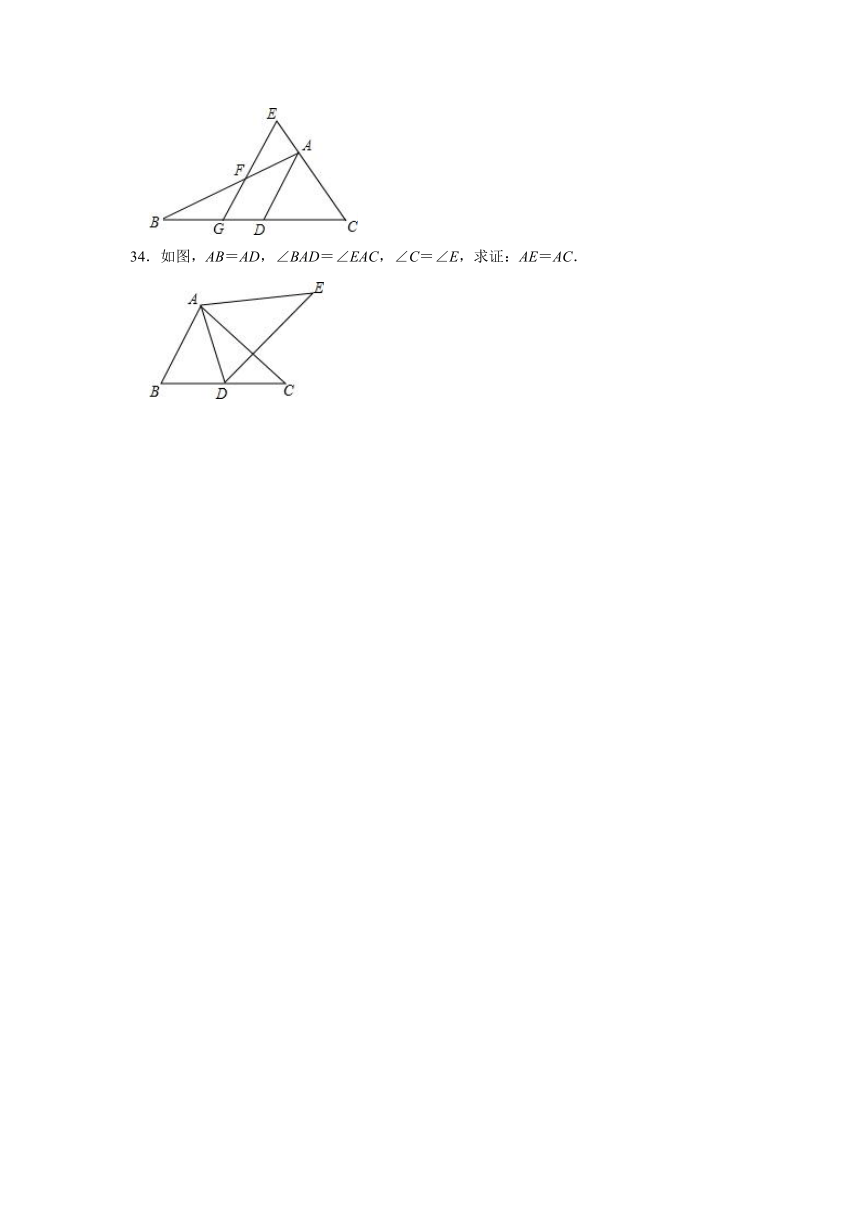
文档简介
鲁教五四新版七年级数学上册
《第1章 三角形》2023年单元测试卷
一.填空题(共12小题)
1.在△ABC中,∠C=100°,∠B=10°,则∠A= .
2.已知△ABC的两条边长分别为2和5,则第三边c的取值范围是 .
3.已知等腰三角形的一个外角是70°,则它顶角的度数为 .
4.如果一个三角形的两边长分别为3.3cm和5.8cm,且第三边的长度为整数,则第三边最短的长度为 .
5.如图,在△ABC中,∠1=∠2,∠3=∠4,∠A=65°,则∠F= .
6.若一个三角形三个内角度数的比为1:2:3,则这个三角形是 .
7.三角形按边分类可分为:三边都不相等的三角形和 三角形两类.
8.将直角三角形(∠ACB为直角)沿线段CD折叠,使B落在B′处,若∠ACB′=60°,则∠ACD= .
9.如果一个三角形的一个内角等于另外两个内角的差,那么这个三角形是 三角形.
10.△ABC的三个内角之比为3:4:5,则这三个内角中最大的内角为 .
11.在△ABC中,∠A=∠B=∠C,则∠C= .
12.等腰三角形的两边分别是2和5,第三边的长度为 .
二.填空题(共6小题)
13.如图,在△ABC中,∠A的对边是 ;在△ABD中,∠A的对边是 .
14.△ABC中,AB=AC,点D为BC上一点,且DA=DB,此时△ACD也恰好为等腰三角形,则∠BAC= .
15.如图,在△ABC中,它的三个内角分别是 , , ,三条边分别是 , , .
16.图中有 个三角形.
17.如图,直角三角形的个数为 .
18.已知△ABC的三个内角的度数之比∠A:∠B:∠C=2:3:5,则∠B= °,∠C= °.
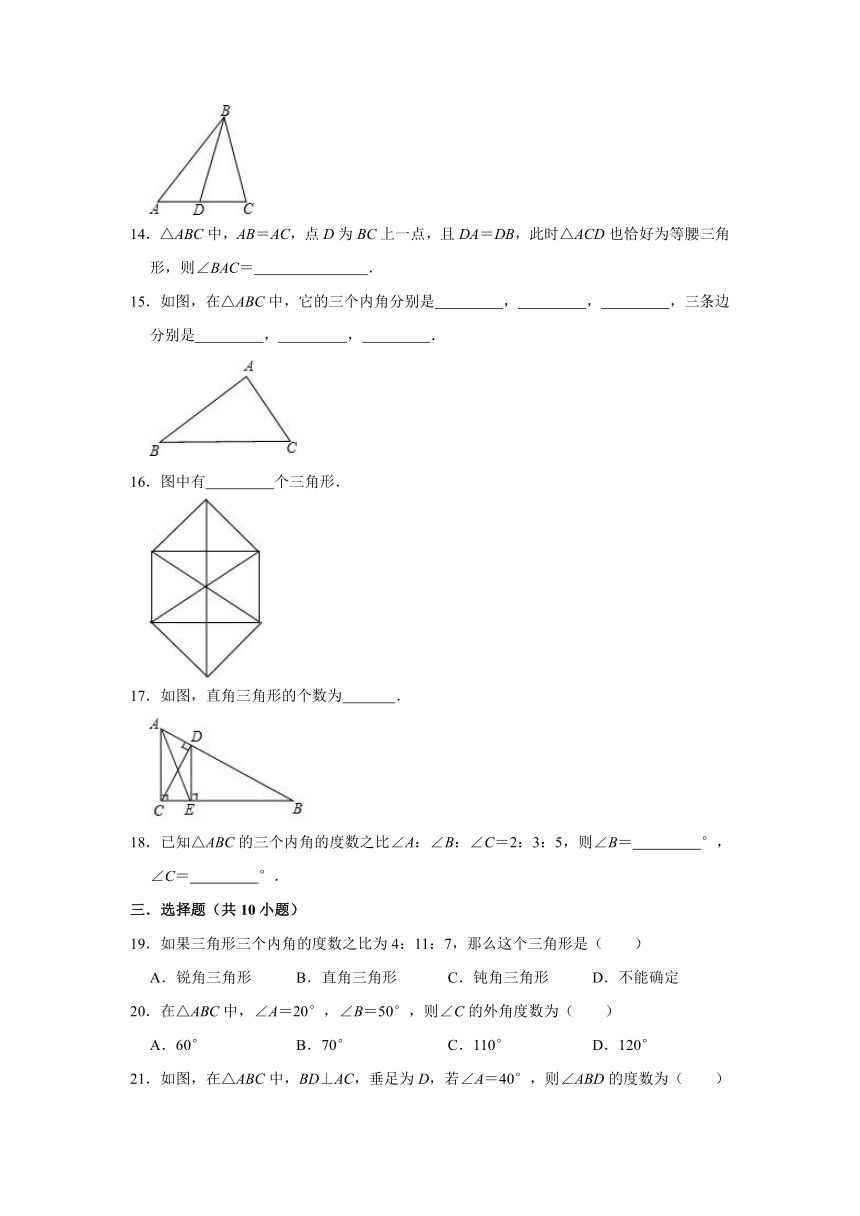
三.选择题(共10小题)
19.如果三角形三个内角的度数之比为4:11:7,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
20.在△ABC中,∠A=20°,∠B=50°,则∠C的外角度数为( )
A.60° B.70° C.110° D.120°
21.如图,在△ABC中,BD⊥AC,垂足为D,若∠A=40°,则∠ABD的度数为( )
A.60° B.50° C.40° D.30°
22.一钝角三角形的钝角为120°,则其两锐角的角平分线相交所夹的钝角为( )
A.120° B.135° C.145° D.150°
23.一个等腰三角形有两边分别为5厘米和8厘米,则周长是( )
A.18厘米 B.21厘米
C.18厘米或21厘米 D.无法确定
24.下列各组长度的线段,能构成三角形的一组是( )
A.1cm,3cm,2cm B.3.5cm,7.1cm,3.6cm
C.6cm,1cm,6cm D.4cm,10cm,4cm
25.当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“标准三角形”,其中α为“标准角”,如果一个“标准三角形”的“标准角”为100°,那么这个“标准三角形”的最小内角度数为( )
A.30° B.45° C.50° D.60°
26.如图,BE、CF是△ABC的角平分线,∠ABC=80°,∠ACB=60°,BE、CF相交于D,则∠BDC的度数是( )
A.110° B.70° C.80° D.75°
27.五条线段的长度分别为1cm、2cm、3cm、4cm、5cm,以其中的三条线段组成三角形,则可组成不同的三角形的个数是( )
A.1个 B.2个 C.3个 D.4个
28.在△ABC中,∠C=80°,∠B=60°,那么∠A的度数是( )
A.20° B.40° C.60° D.70°
四.解答题(共6小题)
29.如图,E、F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.求证:△AFD≌△CEB.
30.如图,已知BE⊥AD,CF⊥AD,请判断△CDF与△BDE是否全等,若全等请写出证明过程,若不全等请你添加一个条件使它们全等,并写出证明过程.
31.如图,AD和BC相交于点O,BE⊥AD于点E,DF⊥BC于点F,BE=DF,∠ABC=∠CDA.求证:AB=CD.
32.如图,已知BD⊥AC,CF⊥AB.
(1)若BE=AC,求证:△BFE≌△CFA.
(2)取BC中点为G,连接FG,DG,求证:FG=DG.
33.已知,如图,在△ABC中,AD平分∠BAC,E是CA延长线上的一点,EG∥AD,交AB于F,求证:AE=AF.
34.如图,AB=AD,∠BAD=∠EAC,∠C=∠E,求证:AE=AC.
鲁教五四新版七年级数学上册
《第1章 三角形》2023年单元测试卷
参考答案与试题解析
一.填空题(共12小题)
1.【解答】解:∵在△ABC中,∠C=100°,∠B=10°,
∴∠A=180°﹣∠B﹣∠C=180°﹣10°﹣100°=70°,
故答案为:70°.
2.【解答】解:由题意,得
5﹣2<c<5+2,
即3<c<7.
故答案为:3<c<7.
3.【解答】解:等腰三角形一个外角为70°,那相邻的内角为110°,
三角形内角和为180°,如果这个内角为底角,内角和将超过180°,
所以110°只可能是顶角.
故答案为:110°.
4.【解答】解:设第三边为a,
根据三角形的三边关系,得:5.8﹣3.3<a<3.3+5.8,
即2.5<a<9.1,
∵a为整数,
∴a的最小值为3.
故答案为:3cm.
5.【解答】解:∵∠A=65°,
∴∠ABC+∠ACB=115°,
∵∠1=∠2,∠3=∠4,
∴∠2+∠4=×115°=57.5°,
∴∠F=180°﹣(∠2+∠4)=122.5°.
故答案为:122.5°.
6.【解答】解:∵一个三角形三个内角度数的比为1:2:3,
∴设三角形的三个内角分别是x,2x,3x,
∴x+2x+3x=180°,解得x=30°,
∴3x=90°.
故答案为:直角三角形.
7.【解答】解:三角形按边分类可以分为不等边三角形和等腰三角形;
故答案为:等腰.
8.【解答】解:∵△B′CD时由△BCD翻折得到的,
∴∠BCD=∠B′CD,
又∵∠BCD+∠B′CD=∠B′CB=∠ACB+∠ACB′=90°+60°=150°,
∴∠BCD=75°,
又∵∠ACD+∠BCD=∠ACB=90°,
∴∠ACD=15°.
故答案为:15°.
9.【解答】解:
∵∠A+∠B+∠C=180°,∠C=∠A+∠B,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,
故答案为:直角.
10.【解答】解:设三角形的三个内角的度数分别为3x,4x,5x,
所以3x+4x+5x=180°,
解得x=15°,
所以5x=75°.
故答案为:75°.
11.【解答】解:∵∠A=∠B=∠C,
则设∠A=x,则∠B=x,∠C=10x,
∵∠A+∠B+∠C=180°,
∴x+x+10x=180°,
解得x=15°,
∴∠C=10×15°=150°,
故答案为:150°.
12.【解答】解:①若腰长为2,则底边为5,
2+2<5,
不能构成三角形.
②若腰长为5,则底边为2
第三边为5.
故答案为:5
二.填空题(共6小题)
13.【解答】解:在△ABC中,∠A的对边是BC;
在△ABD中,∠A的对边是BD;
故答案为:BC;BD.
14.【解答】解:∵AB=AC,
∴∠B=∠C,
∵AD=BD,
∴∠BAD=∠B,
∵△ACD也恰好为等腰三角形,
如图1,当AD=CD,
∴∠CAD=∠C,
∴∠BAC=×180°=90°,
如图2,当AC=CD,
∴∠CAD=∠ADC,
∵∠ADC=∠B+∠BAD=2∠B,
∵∠C+∠CAD+∠ADC=180°,
∴∠C+2∠C+2∠C=180°,
∴∠C=36°,
∴∠BAD=36°,∠CAD=72°,
∴∠BAC=108°.
故答案为:90°或108°.
15.【解答】解:组成△ABC的线段是AC、AB、BC.在△ABC里面的三个角∠A、∠B、∠C叫做三角形的三个内角;
故答案为:∠A、∠B、∠C、AB、AC、BC.
16.【解答】解:图中有10+8+4=22个三角形,
故答案为:22.
17.【解答】解:如图,直角三角形有:△ADC、△BCD、△CDE、△BDE、△ACE、△ACB,一共6个,
故答案为:6.
18.【解答】解:∵∠A+∠B+∠C=180°,∠A:∠B:∠C=2:3:5,
∴∠C=×180°=90°,∠B=×180°=54°,
故答案为:54,90.
三.选择题(共10小题)
19.【解答】解:∵三角形三个内角度数的比为11:7:4,
∴设三个内角度数分别为11x°,7x°,4x°,由题意得:
11x+7x+4x=180,
解得:x=,
11x=,
所以是直角三角形,
故选:B.
20.【解答】解:∵△ABC中,∠A=20°,∠B=50°,
∴∠C=180°﹣(∠A+∠B)=180°﹣(20°+50°)=110°,
∴∠C的外角=180°﹣∠C=180°﹣110°=70°.
故选:B.
21.【解答】解:∵BD⊥AC,
∴∠ADB=90°,
∵∠A=40°,
∴∠ABD=90°﹣40°=50°.
故选:B.
22.【解答】解:∵有一个角为120°,
∴另两个角的度数和为180°﹣120°=60°,
∴另两个角被角平分线所分成的角的和为30°,
根据三角形内角和定理可求出另两个角的角平分线所夹的钝角为180°﹣30°=150°.
故选:D.
23.【解答】解:∵等腰三角形两边为5和8厘米
∴等腰三角形三边可能为5,5,8或5,8,8
∴周长可能为18或21厘米.
故选:C.
24.【解答】解:根据三角形任意两边的和大于第三边,得
A中,1+2=3,不能组成三角形;
B中,3.5+3.6=7.1,不能组成三角形;
C中,1+6=7>6,能够组成三角形;
D中,4+4=8<10,不能组成三角形.
故选:C.
25.【解答】解:由题意得:α=2β,α=100°,则β=50°,
180°﹣100°﹣50°=30°,
故选:A.
26.【解答】解:∵BE、CF是△ABC的角平分线,∠ABC=80°,∠ACB=60°,
∴∠CBE=∠ABC=40°,∠FCB=∠ACB=30°,
∴∠BDC=180°﹣70°=110°.
故选:A.
27.【解答】解:以其中的三条线段为边组成三角形的有:2cm,3cm,4cm;2cm,4cm,5cm;3cm,4cm,5cm共有3种情况.
故选:C.
28.【解答】解:∠A=180°﹣∠B﹣∠C=180°﹣60°﹣80°=40°.
故选:B.
四.解答题(共6小题)
29.【解答】证明:∵DF∥BE,
∴∠DFA=∠CEB,
在△ADF和△CBE中,
,
∴△AFD≌△CEB(SAS).
30.【解答】解:添加的条件为BD=DC,证明如下:
∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°.
在△CDF和△BDE中,
∵,
∴△CDF≌△BDE(AAS).
31.【解答】证明:∵△OBE和△ODF中,,
∴△OBE≌△ODF,
∴OB=OD,
∴在△ABO和△CDO中,,
∴△ABO≌△CDO,
∴AB=CD.
32.【解答】证明:(1)∵BD⊥AC,CF⊥AB,
∴∠BFE=∠CFA=90°,
∵∠BEF=∠CED,
∴∠FBE=∠FCA,
在△BFE和△CFA中,
∴△BFE≌△CFA(AAS);
(2)∵BD⊥AC,CF⊥AB,
∴△BFC和△BDC都是直角三角形,
∵点G是BC边的中点,
∴BC=2FG,BC=2DG,
∴FG=DG.
33.【解答】证明:∵AD是△ABC的平分线,
∴∠BAD=∠CAD,
∵GE∥AD,
∴∠AFE=∠BAD,∠E=∠CAD,
∴∠AFE=∠G,
∴AE=AF.
34.【解答】证明:∵∠BAD=∠EAC,
∴∠BAD+∠DAC=∠EAC+∠DAC,
即∠BAC=∠DAE,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(AAS),
∴AE=AC.
《第1章 三角形》2023年单元测试卷
一.填空题(共12小题)
1.在△ABC中,∠C=100°,∠B=10°,则∠A= .
2.已知△ABC的两条边长分别为2和5,则第三边c的取值范围是 .
3.已知等腰三角形的一个外角是70°,则它顶角的度数为 .
4.如果一个三角形的两边长分别为3.3cm和5.8cm,且第三边的长度为整数,则第三边最短的长度为 .
5.如图,在△ABC中,∠1=∠2,∠3=∠4,∠A=65°,则∠F= .
6.若一个三角形三个内角度数的比为1:2:3,则这个三角形是 .
7.三角形按边分类可分为:三边都不相等的三角形和 三角形两类.
8.将直角三角形(∠ACB为直角)沿线段CD折叠,使B落在B′处,若∠ACB′=60°,则∠ACD= .
9.如果一个三角形的一个内角等于另外两个内角的差,那么这个三角形是 三角形.
10.△ABC的三个内角之比为3:4:5,则这三个内角中最大的内角为 .
11.在△ABC中,∠A=∠B=∠C,则∠C= .
12.等腰三角形的两边分别是2和5,第三边的长度为 .
二.填空题(共6小题)
13.如图,在△ABC中,∠A的对边是 ;在△ABD中,∠A的对边是 .
14.△ABC中,AB=AC,点D为BC上一点,且DA=DB,此时△ACD也恰好为等腰三角形,则∠BAC= .
15.如图,在△ABC中,它的三个内角分别是 , , ,三条边分别是 , , .
16.图中有 个三角形.
17.如图,直角三角形的个数为 .
18.已知△ABC的三个内角的度数之比∠A:∠B:∠C=2:3:5,则∠B= °,∠C= °.
三.选择题(共10小题)
19.如果三角形三个内角的度数之比为4:11:7,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
20.在△ABC中,∠A=20°,∠B=50°,则∠C的外角度数为( )
A.60° B.70° C.110° D.120°
21.如图,在△ABC中,BD⊥AC,垂足为D,若∠A=40°,则∠ABD的度数为( )
A.60° B.50° C.40° D.30°
22.一钝角三角形的钝角为120°,则其两锐角的角平分线相交所夹的钝角为( )
A.120° B.135° C.145° D.150°
23.一个等腰三角形有两边分别为5厘米和8厘米,则周长是( )
A.18厘米 B.21厘米
C.18厘米或21厘米 D.无法确定
24.下列各组长度的线段,能构成三角形的一组是( )
A.1cm,3cm,2cm B.3.5cm,7.1cm,3.6cm
C.6cm,1cm,6cm D.4cm,10cm,4cm
25.当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“标准三角形”,其中α为“标准角”,如果一个“标准三角形”的“标准角”为100°,那么这个“标准三角形”的最小内角度数为( )
A.30° B.45° C.50° D.60°
26.如图,BE、CF是△ABC的角平分线,∠ABC=80°,∠ACB=60°,BE、CF相交于D,则∠BDC的度数是( )
A.110° B.70° C.80° D.75°
27.五条线段的长度分别为1cm、2cm、3cm、4cm、5cm,以其中的三条线段组成三角形,则可组成不同的三角形的个数是( )
A.1个 B.2个 C.3个 D.4个
28.在△ABC中,∠C=80°,∠B=60°,那么∠A的度数是( )
A.20° B.40° C.60° D.70°
四.解答题(共6小题)
29.如图,E、F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.求证:△AFD≌△CEB.
30.如图,已知BE⊥AD,CF⊥AD,请判断△CDF与△BDE是否全等,若全等请写出证明过程,若不全等请你添加一个条件使它们全等,并写出证明过程.
31.如图,AD和BC相交于点O,BE⊥AD于点E,DF⊥BC于点F,BE=DF,∠ABC=∠CDA.求证:AB=CD.
32.如图,已知BD⊥AC,CF⊥AB.
(1)若BE=AC,求证:△BFE≌△CFA.
(2)取BC中点为G,连接FG,DG,求证:FG=DG.
33.已知,如图,在△ABC中,AD平分∠BAC,E是CA延长线上的一点,EG∥AD,交AB于F,求证:AE=AF.
34.如图,AB=AD,∠BAD=∠EAC,∠C=∠E,求证:AE=AC.
鲁教五四新版七年级数学上册
《第1章 三角形》2023年单元测试卷
参考答案与试题解析
一.填空题(共12小题)
1.【解答】解:∵在△ABC中,∠C=100°,∠B=10°,
∴∠A=180°﹣∠B﹣∠C=180°﹣10°﹣100°=70°,
故答案为:70°.
2.【解答】解:由题意,得
5﹣2<c<5+2,
即3<c<7.
故答案为:3<c<7.
3.【解答】解:等腰三角形一个外角为70°,那相邻的内角为110°,
三角形内角和为180°,如果这个内角为底角,内角和将超过180°,
所以110°只可能是顶角.
故答案为:110°.
4.【解答】解:设第三边为a,
根据三角形的三边关系,得:5.8﹣3.3<a<3.3+5.8,
即2.5<a<9.1,
∵a为整数,
∴a的最小值为3.
故答案为:3cm.
5.【解答】解:∵∠A=65°,
∴∠ABC+∠ACB=115°,
∵∠1=∠2,∠3=∠4,
∴∠2+∠4=×115°=57.5°,
∴∠F=180°﹣(∠2+∠4)=122.5°.
故答案为:122.5°.
6.【解答】解:∵一个三角形三个内角度数的比为1:2:3,
∴设三角形的三个内角分别是x,2x,3x,
∴x+2x+3x=180°,解得x=30°,
∴3x=90°.
故答案为:直角三角形.
7.【解答】解:三角形按边分类可以分为不等边三角形和等腰三角形;
故答案为:等腰.
8.【解答】解:∵△B′CD时由△BCD翻折得到的,
∴∠BCD=∠B′CD,
又∵∠BCD+∠B′CD=∠B′CB=∠ACB+∠ACB′=90°+60°=150°,
∴∠BCD=75°,
又∵∠ACD+∠BCD=∠ACB=90°,
∴∠ACD=15°.
故答案为:15°.
9.【解答】解:
∵∠A+∠B+∠C=180°,∠C=∠A+∠B,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,
故答案为:直角.
10.【解答】解:设三角形的三个内角的度数分别为3x,4x,5x,
所以3x+4x+5x=180°,
解得x=15°,
所以5x=75°.
故答案为:75°.
11.【解答】解:∵∠A=∠B=∠C,
则设∠A=x,则∠B=x,∠C=10x,
∵∠A+∠B+∠C=180°,
∴x+x+10x=180°,
解得x=15°,
∴∠C=10×15°=150°,
故答案为:150°.
12.【解答】解:①若腰长为2,则底边为5,
2+2<5,
不能构成三角形.
②若腰长为5,则底边为2
第三边为5.
故答案为:5
二.填空题(共6小题)
13.【解答】解:在△ABC中,∠A的对边是BC;
在△ABD中,∠A的对边是BD;
故答案为:BC;BD.
14.【解答】解:∵AB=AC,
∴∠B=∠C,
∵AD=BD,
∴∠BAD=∠B,
∵△ACD也恰好为等腰三角形,
如图1,当AD=CD,
∴∠CAD=∠C,
∴∠BAC=×180°=90°,
如图2,当AC=CD,
∴∠CAD=∠ADC,
∵∠ADC=∠B+∠BAD=2∠B,
∵∠C+∠CAD+∠ADC=180°,
∴∠C+2∠C+2∠C=180°,
∴∠C=36°,
∴∠BAD=36°,∠CAD=72°,
∴∠BAC=108°.
故答案为:90°或108°.
15.【解答】解:组成△ABC的线段是AC、AB、BC.在△ABC里面的三个角∠A、∠B、∠C叫做三角形的三个内角;
故答案为:∠A、∠B、∠C、AB、AC、BC.
16.【解答】解:图中有10+8+4=22个三角形,
故答案为:22.
17.【解答】解:如图,直角三角形有:△ADC、△BCD、△CDE、△BDE、△ACE、△ACB,一共6个,
故答案为:6.
18.【解答】解:∵∠A+∠B+∠C=180°,∠A:∠B:∠C=2:3:5,
∴∠C=×180°=90°,∠B=×180°=54°,
故答案为:54,90.
三.选择题(共10小题)
19.【解答】解:∵三角形三个内角度数的比为11:7:4,
∴设三个内角度数分别为11x°,7x°,4x°,由题意得:
11x+7x+4x=180,
解得:x=,
11x=,
所以是直角三角形,
故选:B.
20.【解答】解:∵△ABC中,∠A=20°,∠B=50°,
∴∠C=180°﹣(∠A+∠B)=180°﹣(20°+50°)=110°,
∴∠C的外角=180°﹣∠C=180°﹣110°=70°.
故选:B.
21.【解答】解:∵BD⊥AC,
∴∠ADB=90°,
∵∠A=40°,
∴∠ABD=90°﹣40°=50°.
故选:B.
22.【解答】解:∵有一个角为120°,
∴另两个角的度数和为180°﹣120°=60°,
∴另两个角被角平分线所分成的角的和为30°,
根据三角形内角和定理可求出另两个角的角平分线所夹的钝角为180°﹣30°=150°.
故选:D.
23.【解答】解:∵等腰三角形两边为5和8厘米
∴等腰三角形三边可能为5,5,8或5,8,8
∴周长可能为18或21厘米.
故选:C.
24.【解答】解:根据三角形任意两边的和大于第三边,得
A中,1+2=3,不能组成三角形;
B中,3.5+3.6=7.1,不能组成三角形;
C中,1+6=7>6,能够组成三角形;
D中,4+4=8<10,不能组成三角形.
故选:C.
25.【解答】解:由题意得:α=2β,α=100°,则β=50°,
180°﹣100°﹣50°=30°,
故选:A.
26.【解答】解:∵BE、CF是△ABC的角平分线,∠ABC=80°,∠ACB=60°,
∴∠CBE=∠ABC=40°,∠FCB=∠ACB=30°,
∴∠BDC=180°﹣70°=110°.
故选:A.
27.【解答】解:以其中的三条线段为边组成三角形的有:2cm,3cm,4cm;2cm,4cm,5cm;3cm,4cm,5cm共有3种情况.
故选:C.
28.【解答】解:∠A=180°﹣∠B﹣∠C=180°﹣60°﹣80°=40°.
故选:B.
四.解答题(共6小题)
29.【解答】证明:∵DF∥BE,
∴∠DFA=∠CEB,
在△ADF和△CBE中,
,
∴△AFD≌△CEB(SAS).
30.【解答】解:添加的条件为BD=DC,证明如下:
∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°.
在△CDF和△BDE中,
∵,
∴△CDF≌△BDE(AAS).
31.【解答】证明:∵△OBE和△ODF中,,
∴△OBE≌△ODF,
∴OB=OD,
∴在△ABO和△CDO中,,
∴△ABO≌△CDO,
∴AB=CD.
32.【解答】证明:(1)∵BD⊥AC,CF⊥AB,
∴∠BFE=∠CFA=90°,
∵∠BEF=∠CED,
∴∠FBE=∠FCA,
在△BFE和△CFA中,
∴△BFE≌△CFA(AAS);
(2)∵BD⊥AC,CF⊥AB,
∴△BFC和△BDC都是直角三角形,
∵点G是BC边的中点,
∴BC=2FG,BC=2DG,
∴FG=DG.
33.【解答】证明:∵AD是△ABC的平分线,
∴∠BAD=∠CAD,
∵GE∥AD,
∴∠AFE=∠BAD,∠E=∠CAD,
∴∠AFE=∠G,
∴AE=AF.
34.【解答】证明:∵∠BAD=∠EAC,
∴∠BAD+∠DAC=∠EAC+∠DAC,
即∠BAC=∠DAE,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(AAS),
∴AE=AC.
