第3章 整式及其加减 单元试卷 (含解析)2023-2024学年鲁教版(五四制)六年级数学第一学期
文档属性
| 名称 | 第3章 整式及其加减 单元试卷 (含解析)2023-2024学年鲁教版(五四制)六年级数学第一学期 |  | |
| 格式 | docx | ||
| 文件大小 | 243.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 19:34:28 | ||
图片预览


文档简介
鲁教五四新版六年级(上)单元试卷
第3章 整式及其加减
一.选择题(共10小题)
1.如图,漠漠和嘉嘉做数学游戏:假设嘉嘉抽到牌的点数为x,漠漠猜中的结果为y,则y等于( )
A.2 B.3 C.6 D.x+2
2.用棋子摆出如图所示的一组“口”字,按照这种方法照,则摆第n(n为正整数)个“口”字需用棋子( )枚.
A.4n B.4n﹣4 C.4n+4 D.n2
3.观察下列各图形中小正方形的个数,依此规律,第(11)个图形中小正方形的个数为( )
A.78 B.66 C.55 D.50
4.下列图形是将正三角形按一定规律排列,则第4个图形中所有正三角形的个数有( )
A.160 B.161 C.162 D.163
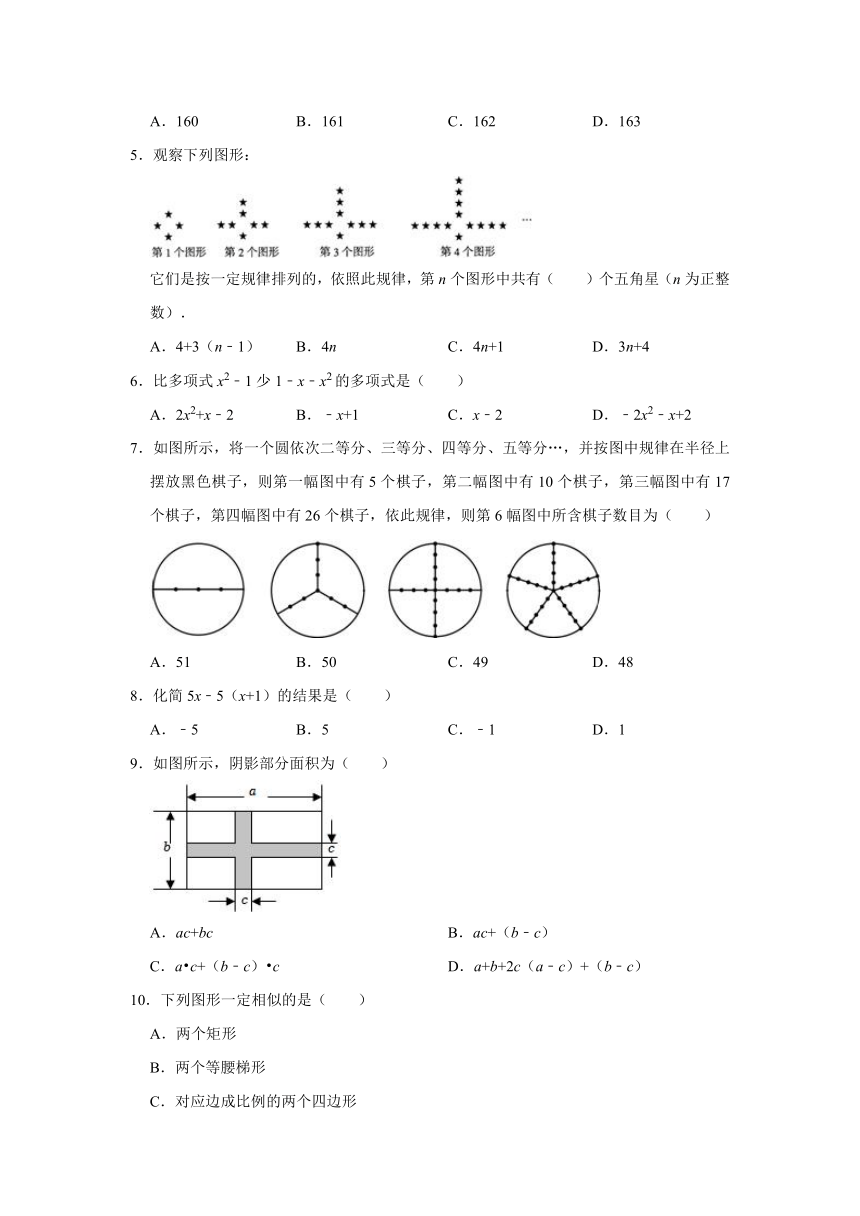
5.观察下列图形:
它们是按一定规律排列的,依照此规律,第n个图形中共有( )个五角星(n为正整数).
A.4+3(n﹣1) B.4n C.4n+1 D.3n+4
6.比多项式x2﹣1少1﹣x﹣x2的多项式是( )
A.2x2+x﹣2 B.﹣x+1 C.x﹣2 D.﹣2x2﹣x+2
7.如图所示,将一个圆依次二等分、三等分、四等分、五等分…,并按图中规律在半径上摆放黑色棋子,则第一幅图中有5个棋子,第二幅图中有10个棋子,第三幅图中有17个棋子,第四幅图中有26个棋子,依此规律,则第6幅图中所含棋子数目为( )
A.51 B.50 C.49 D.48
8.化简5x﹣5(x+1)的结果是( )
A.﹣5 B.5 C.﹣1 D.1
9.如图所示,阴影部分面积为( )
A.ac+bc B.ac+(b﹣c)
C.a c+(b﹣c) c D.a+b+2c(a﹣c)+(b﹣c)
10.下列图形一定相似的是( )
A.两个矩形
B.两个等腰梯形
C.对应边成比例的两个四边形
D.有一个内角相等的菱形
二.填空题(共16小题)
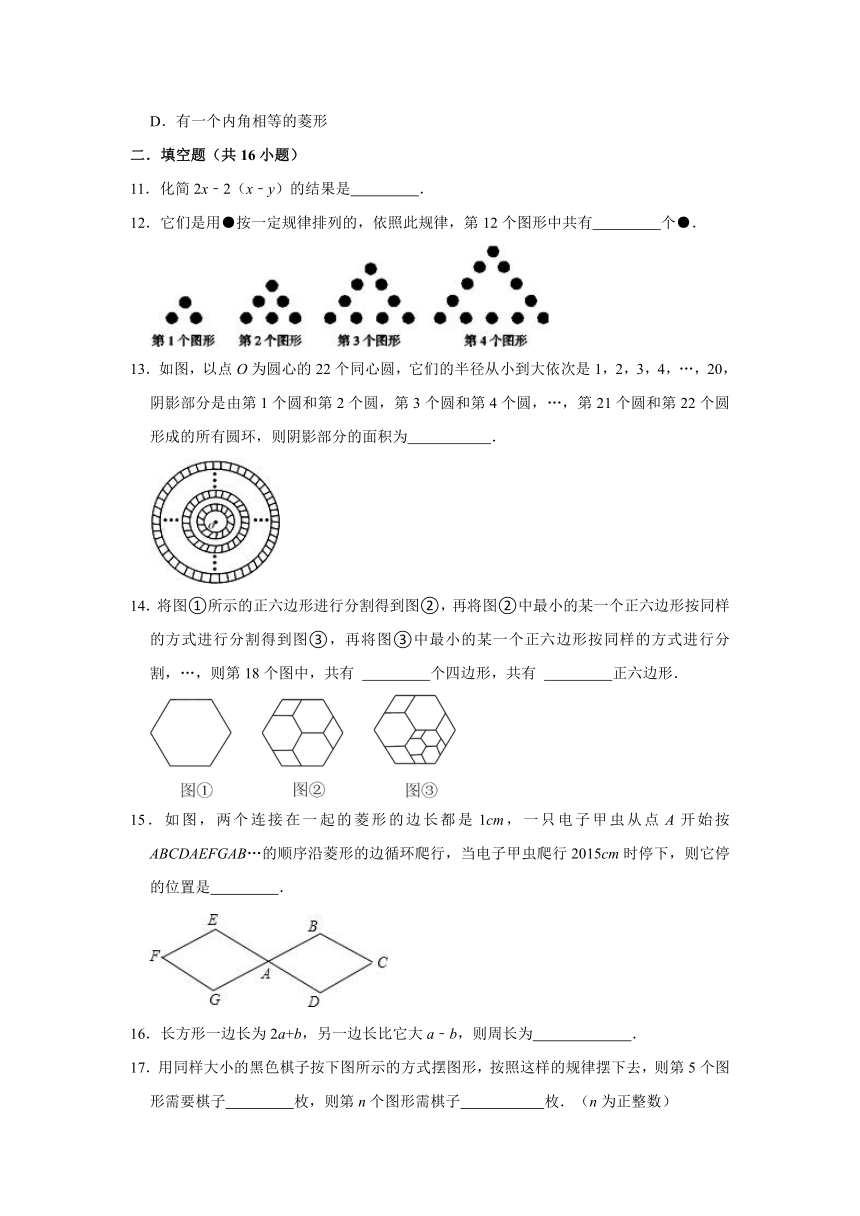
11.化简2x﹣2(x﹣y)的结果是 .
12.它们是用●按一定规律排列的,依照此规律,第12个图形中共有 个●.
13.如图,以点O为圆心的22个同心圆,它们的半径从小到大依次是1,2,3,4,…,20,阴影部分是由第1个圆和第2个圆,第3个圆和第4个圆,…,第21个圆和第22个圆形成的所有圆环,则阴影部分的面积为 .
14.将图①所示的正六边形进行分割得到图②,再将图②中最小的某一个正六边形按同样的方式进行分割得到图③,再将图③中最小的某一个正六边形按同样的方式进行分割,…,则第18个图中,共有 个四边形,共有 正六边形.
15.如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2015cm时停下,则它停的位置是 .
16.长方形一边长为2a+b,另一边长比它大a﹣b,则周长为 .
17.用同样大小的黑色棋子按下图所示的方式摆图形,按照这样的规律摆下去,则第5个图形需要棋子 枚,则第n个图形需棋子 枚.(n为正整数)
18.“梅花朵朵迎春来”,下面四个图形是由小梅花摆成的一组有规律的图案,按图中规律,第n个图形中小梅花的个数是 .
19.在已知的线段AB上取10个点(包括A,B两点),这些点把线段AB共分成 条线段.
20.如图用火柴摆出一系列图案,按这种方式摆下去,当每边摆10根时(即n=10)时,需要的火柴棒总数为 根.
21.高杨同学用木棒和硬币拼成如图所示的“列车”形状,第1个图需要4根木棒,2枚硬币,第2个图需要7根木棒,4枚硬币,照这样的方式摆下去,第n个图需要 根木棒, 枚硬币.
22.下列图形都是由同样大小的五角星按一定的规律组成,其中第①个图形一共有2个五角星,第②个图形一共有8个五角星,第③个图形一共有18个五角星,…,则第⑥个图形中五角星的个数为 .
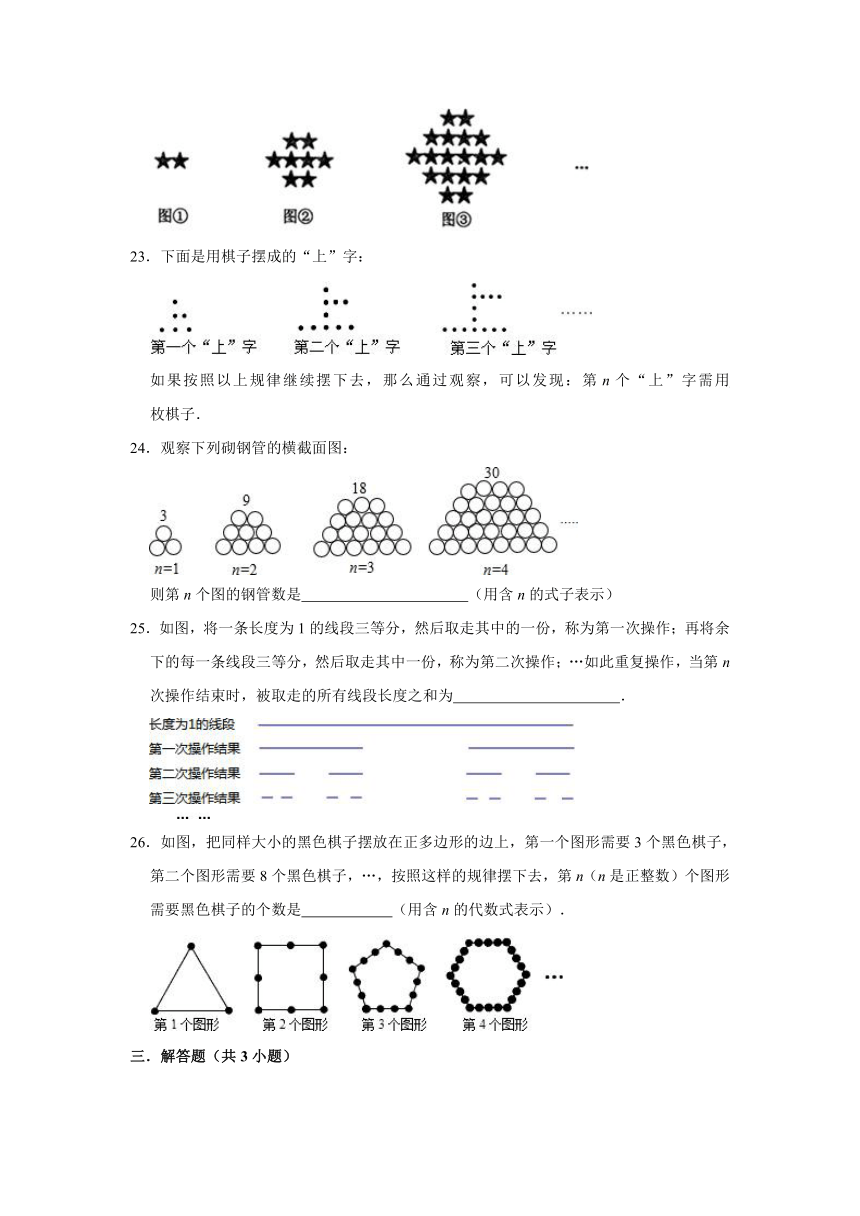
23.下面是用棋子摆成的“上”字:
如果按照以上规律继续摆下去,那么通过观察,可以发现:第n个“上”字需用 枚棋子.
24.观察下列砌钢管的横截面图:
则第n个图的钢管数是 (用含n的式子表示)
25.如图,将一条长度为1的线段三等分,然后取走其中的一份,称为第一次操作;再将余下的每一条线段三等分,然后取走其中一份,称为第二次操作;…如此重复操作,当第n次操作结束时,被取走的所有线段长度之和为 .
26.如图,把同样大小的黑色棋子摆放在正多边形的边上,第一个图形需要3个黑色棋子,第二个图形需要8个黑色棋子,…,按照这样的规律摆下去,第n(n是正整数)个图形需要黑色棋子的个数是 (用含n的代数式表示).
三.解答题(共3小题)
27.先化简,再求值:3a2b﹣[﹣2a2b﹣6(ab﹣a2b)+4ab]﹣3ab,其中a=3,b=﹣.
28.将正六边形纸片按下列要求分割(每次分割,纸片均不得有剩余):
第一次分割:将正六边形纸片分割成三个全等的菱形,然后选取其中的一个菱形在分割成一个正六边形和两个全等的正三角形;
第二次分割:将第一次分割后所得的正六边形纸片分割成三个全等的菱形,然后选取其中的一个菱形在分割成一个正六边形和两个全等的正三角形;
按上述分割方法进行下去…
(1)请你在下图中画出第一次分割的示意图;
(2)若原正六边形的面积为a,请你通过操作和观察,将第1次,第2次,第3次分割后所得的正六边形的面积填入下表:
分割次数(n) 1 2 3 …
正六边形的面积S
(3)观察所填表格,并结合操作,请你猜想:分割后所得的正六边形的面积S与分割次数n有何关系?(S用含a和n的代数式表示,不需要写出推理过程)
29.如图①,是用3根相同火柴棒拼成的一个三角图形,记为一个基本图形,将此基本图形不断的复制,使得相邻的两个基本图形的边重合,这样得到图②,图③…
(1)观察以上图形,图④中所用火柴棒的根数为 ,
猜想:在图n中,所用火柴棒的根数为 (用n表示);
(2)如图,将图n放在直角坐标系中,设其中第一个基本图形的中心O1的坐标为(,y1),则y1= ;O2014的坐标为 .
鲁教五四新版六年级(上)单元试卷
第3章 整式及其加减
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:根据题意得:(3x+6)÷3﹣x=y,
解得:y=2.
故选:A.
2.【解答】解:n=1时,棋子个数为4=1×4;
n=2时,棋子个数为8=2×4;
n=3时,棋子个数为12=3×4;
…;
n=n时,棋子个数为n×4=4n.
故选:A.
3.【解答】解:由题意得:第一个图形中小正方形的个数为1,
第二个为1+2=3,
第三个为1+2+3=6,
第四个为1+2+3+4=10,
…;
第(11)个图形中小正方形的个数为:1+2+3+4+5+6+7+8+9+10+11=66.
故选:B.
4.【解答】方法一:
解:第一个图形正三角形的个数为5,
第二个图形正三角形的个数为5×3+2=17,
第三个图形正三角形的个数为17×3+2=53,
第四个图形正三角形的个数为53×3+2=161,
故选B.
方法二:
,,,,…,
∴,
(a2﹣a1)+(a3﹣a2)+(a4﹣a3)+…+(an﹣an﹣1)=an﹣a1,
∴an﹣a1=4×(3+32+…+3n﹣1)=4×(3+32+…+3n﹣1)=(用错位相减法可求出)
∴,
∵a1=5,
∴.
故选:B.
5.【解答】解:根据已知图形得:
第1个图形五角星个数:1×3+1,
第2个图形五角星个数:2×3+1,
第3个图形五角星个数:3×3+1,
第4个图形五角星个数:4×3+1,
由此规律得:
第2个图形五角星个数:n×3+1,
故第n个图形中共有3n+1个图形;
A答案为4+3(n﹣1)=3n+1.
故选:A.
6.【解答】解:x2﹣1﹣(1﹣x﹣x2)=x2﹣1﹣1+x+x2=2x2+x﹣2.
故选:A.
7.【解答】解:∵第一幅图中有22+1=5个棋子,
第二幅图中有32+1=10个棋子,
第三幅图中有42+1=17个棋子,
第四幅图中有52+1=26个棋子,
…
∴第n幅图中所含棋子数目为(n+1)2+1,
∴第6幅图中所含棋子数目为49+1=50.
故选:B.
8.【解答】解:原式=5x﹣5x﹣5=﹣5.
故选:A.
9.【解答】解:观察图形可知,阴影部分面积为ab﹣(a﹣c)(b﹣c)=ab﹣ab+ac+bc﹣c2=ac+(b﹣c)c.
故选:C.
10.【解答】解:A、两个矩形的对应角相等,但对应边的比不一定相等,故错误;
B、两个等腰梯形不一定相似,故错误;
C、对应边成比例且对应角相等的两个四边形是全等形,故错误;
D、有一个内角相等的菱形是相似图形,故正确,
故选:D.
二.填空题(共16小题)
11.【解答】解:原式=2x﹣2x+2y=2y,
故答案为:2y
12.【解答】解:根据规律可知
第n个图形有3n个●,
所以第12个图形共有12×3=36个●.
故答案为:36.
13.【解答】解:由题意可得:阴影部分的面积和为:
π(22﹣12)+π(42﹣32)+π(62﹣52)+…+π(202﹣192)+π(222﹣212)
=3π+7π+11π+15π+…+39π+43π
=(3π+43π)×11÷2
=253π.
故答案为:253π.
14.【解答】解:观察第二个图形,有3个四边形,1+3=4(个)正六边形,
第三个图形,有6个四边形,1+3+3=7(个)正六边形
依此类推,
第n个图形中,有3(n﹣1)个四边形,1+3(n﹣1)=(3n﹣2)个正六边形.
∴第18个图中,
共有3×(18﹣1)=51(个)四边形,共有3×18﹣2=52(个)正六边形.
故答案为:51,52.
15.【解答】解:一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,从出发到第1次回到点A共爬行了8cm,
而2015=251×8+7,
所以当电子甲虫爬行2015cm时停下,它停的位置是G点.
故点G.
16.【解答】解:另一边的长为:(2a+b)+(a﹣b)=3a.
∴周长为[(2a+b)+3a]×2=10a+2b.
17.【解答】解:第一个图需棋子3+1=4;
第二个图需棋子3×2+1=7;
第三个图需棋子3×3+1=10;
第四个图需棋子3×4+1=13;
第五个图需棋子3×5+1=16;
…
第n个图需棋子3n+1枚.
故答案为:16,3n+1.
18.【解答】解:第1个图案是由2个组成:
即为:2=1×2;
第2个图案是由9个组成:
即为:9=3×3;
第3个图案是由5×4=20个组成:
即为:20=5×4;
第4个图案是由35个组成:
即为:35=7×5;
以此类推:第n个图案的个数:(2n﹣1)(n+1).
故答案为:(2n﹣1)(n+1).
19.【解答】解:设线段有n个点,分成的线段有m条,有以下规律:
n个m条
2 1
3 1+2
4 1+2+3
:
:
:
n m=1+…+(n﹣1)=
10个点把线段AB共分成=45条.
20.【解答】解:通过图形变化可知:
n=1时 火柴棒总数为 3×1
n=2时 火柴棒总数为 3×(1+2),
n=3时 火柴棒总数为 3(1+2+3),
∴n=10时 火柴棒总数为 3×(1+2+3+…+9+10)
故答案为165
21.【解答】解:第1个图形需要木棒4=1+3×1根,硬币2=2×1枚;
第2个图形需要木棒7=1+3×2根,硬币4=2×2枚;
第3个图形需要木棒10=1+3×3根,硬币6=2×3枚;
…
则第n个图形需要木棒数为:1+3n,硬币:2n.
故答案为:(3n+1),2n.
22.【解答】解:第①个图形中五角星的个数为2=2×12;
第②个图形中五角星的个数为2+4+2=8=2×4=2×22;
第③个图形中五角星的个数为2+4+6+4+2=18=2×32;
第④个图形中五角星的个数为2×42;
所以第⑥个图形中五角星的个数为2×62=2×36=72.
故答案为72.
23.【解答】解:“上”字共有四个端点每次每个端点增加一枚棋子,而初始时内部有两枚棋子不发生变化,
所以第n个字需要4n+2枚棋子.
故答案为:4n+2.
24.【解答】解:第一个图中钢管数为1+2=3;
第二个图中钢管数为2+3+4=9;
第三个图中钢管数为3+4+5+6=18;
第四个图中钢管数为4+5+6+7+8=30,
依此类推,第n个图中钢管数为n+(n+1)+(n+2)+…+2n=+=n2+n,
故答案为:n2+n.
25.【解答】解:第一次操作后余下的线段之和为1﹣,
第二次操作后余下的线段之和为(1﹣)2,
…
第n次操作后余下的线段之和为(1﹣)n=,
则被取走的所有线段长度之和为1﹣.
故答案为:1﹣.
26.【解答】解:结合图形,发现:
第n(n是正整数)个图形需要黑色棋子的个数是n(n+2)=n2+2n(个).
三.解答题(共3小题)
27.【解答】解:原式=3a2b+2a2b+6ab﹣4a2b﹣4ab﹣3ab=a2b﹣ab,
当a=3,b=﹣时,原式=﹣3+1=﹣2.
28.【解答】(1)如图:
;
(2)
分割次数(n) 1 2 3 …
正六边形的面积S …
;
(3).
29.【解答】解:(1)观察以上图形,图④中所用火柴棒的根数为9,
猜想:在图n中,所用火柴棒的根数为2n+1(用n表示);
(2)将图n放在直角坐标系中,设其中第一个基本图形的中心O1的坐标为(,y1),O2的坐标为(2,2),O3的坐标为(3,1),O4的坐标为(4,2),…O2014的坐标为(2014,2).
故答案为:(1)9;2n+1;(2)1;(2014,2).
第3章 整式及其加减
一.选择题(共10小题)
1.如图,漠漠和嘉嘉做数学游戏:假设嘉嘉抽到牌的点数为x,漠漠猜中的结果为y,则y等于( )
A.2 B.3 C.6 D.x+2
2.用棋子摆出如图所示的一组“口”字,按照这种方法照,则摆第n(n为正整数)个“口”字需用棋子( )枚.
A.4n B.4n﹣4 C.4n+4 D.n2
3.观察下列各图形中小正方形的个数,依此规律,第(11)个图形中小正方形的个数为( )
A.78 B.66 C.55 D.50
4.下列图形是将正三角形按一定规律排列,则第4个图形中所有正三角形的个数有( )
A.160 B.161 C.162 D.163
5.观察下列图形:
它们是按一定规律排列的,依照此规律,第n个图形中共有( )个五角星(n为正整数).
A.4+3(n﹣1) B.4n C.4n+1 D.3n+4
6.比多项式x2﹣1少1﹣x﹣x2的多项式是( )
A.2x2+x﹣2 B.﹣x+1 C.x﹣2 D.﹣2x2﹣x+2
7.如图所示,将一个圆依次二等分、三等分、四等分、五等分…,并按图中规律在半径上摆放黑色棋子,则第一幅图中有5个棋子,第二幅图中有10个棋子,第三幅图中有17个棋子,第四幅图中有26个棋子,依此规律,则第6幅图中所含棋子数目为( )
A.51 B.50 C.49 D.48
8.化简5x﹣5(x+1)的结果是( )
A.﹣5 B.5 C.﹣1 D.1
9.如图所示,阴影部分面积为( )
A.ac+bc B.ac+(b﹣c)
C.a c+(b﹣c) c D.a+b+2c(a﹣c)+(b﹣c)
10.下列图形一定相似的是( )
A.两个矩形
B.两个等腰梯形
C.对应边成比例的两个四边形
D.有一个内角相等的菱形
二.填空题(共16小题)
11.化简2x﹣2(x﹣y)的结果是 .
12.它们是用●按一定规律排列的,依照此规律,第12个图形中共有 个●.
13.如图,以点O为圆心的22个同心圆,它们的半径从小到大依次是1,2,3,4,…,20,阴影部分是由第1个圆和第2个圆,第3个圆和第4个圆,…,第21个圆和第22个圆形成的所有圆环,则阴影部分的面积为 .
14.将图①所示的正六边形进行分割得到图②,再将图②中最小的某一个正六边形按同样的方式进行分割得到图③,再将图③中最小的某一个正六边形按同样的方式进行分割,…,则第18个图中,共有 个四边形,共有 正六边形.
15.如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2015cm时停下,则它停的位置是 .
16.长方形一边长为2a+b,另一边长比它大a﹣b,则周长为 .
17.用同样大小的黑色棋子按下图所示的方式摆图形,按照这样的规律摆下去,则第5个图形需要棋子 枚,则第n个图形需棋子 枚.(n为正整数)
18.“梅花朵朵迎春来”,下面四个图形是由小梅花摆成的一组有规律的图案,按图中规律,第n个图形中小梅花的个数是 .
19.在已知的线段AB上取10个点(包括A,B两点),这些点把线段AB共分成 条线段.
20.如图用火柴摆出一系列图案,按这种方式摆下去,当每边摆10根时(即n=10)时,需要的火柴棒总数为 根.
21.高杨同学用木棒和硬币拼成如图所示的“列车”形状,第1个图需要4根木棒,2枚硬币,第2个图需要7根木棒,4枚硬币,照这样的方式摆下去,第n个图需要 根木棒, 枚硬币.
22.下列图形都是由同样大小的五角星按一定的规律组成,其中第①个图形一共有2个五角星,第②个图形一共有8个五角星,第③个图形一共有18个五角星,…,则第⑥个图形中五角星的个数为 .
23.下面是用棋子摆成的“上”字:
如果按照以上规律继续摆下去,那么通过观察,可以发现:第n个“上”字需用 枚棋子.
24.观察下列砌钢管的横截面图:
则第n个图的钢管数是 (用含n的式子表示)
25.如图,将一条长度为1的线段三等分,然后取走其中的一份,称为第一次操作;再将余下的每一条线段三等分,然后取走其中一份,称为第二次操作;…如此重复操作,当第n次操作结束时,被取走的所有线段长度之和为 .
26.如图,把同样大小的黑色棋子摆放在正多边形的边上,第一个图形需要3个黑色棋子,第二个图形需要8个黑色棋子,…,按照这样的规律摆下去,第n(n是正整数)个图形需要黑色棋子的个数是 (用含n的代数式表示).
三.解答题(共3小题)
27.先化简,再求值:3a2b﹣[﹣2a2b﹣6(ab﹣a2b)+4ab]﹣3ab,其中a=3,b=﹣.
28.将正六边形纸片按下列要求分割(每次分割,纸片均不得有剩余):
第一次分割:将正六边形纸片分割成三个全等的菱形,然后选取其中的一个菱形在分割成一个正六边形和两个全等的正三角形;
第二次分割:将第一次分割后所得的正六边形纸片分割成三个全等的菱形,然后选取其中的一个菱形在分割成一个正六边形和两个全等的正三角形;
按上述分割方法进行下去…
(1)请你在下图中画出第一次分割的示意图;
(2)若原正六边形的面积为a,请你通过操作和观察,将第1次,第2次,第3次分割后所得的正六边形的面积填入下表:
分割次数(n) 1 2 3 …
正六边形的面积S
(3)观察所填表格,并结合操作,请你猜想:分割后所得的正六边形的面积S与分割次数n有何关系?(S用含a和n的代数式表示,不需要写出推理过程)
29.如图①,是用3根相同火柴棒拼成的一个三角图形,记为一个基本图形,将此基本图形不断的复制,使得相邻的两个基本图形的边重合,这样得到图②,图③…
(1)观察以上图形,图④中所用火柴棒的根数为 ,
猜想:在图n中,所用火柴棒的根数为 (用n表示);
(2)如图,将图n放在直角坐标系中,设其中第一个基本图形的中心O1的坐标为(,y1),则y1= ;O2014的坐标为 .
鲁教五四新版六年级(上)单元试卷
第3章 整式及其加减
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:根据题意得:(3x+6)÷3﹣x=y,
解得:y=2.
故选:A.
2.【解答】解:n=1时,棋子个数为4=1×4;
n=2时,棋子个数为8=2×4;
n=3时,棋子个数为12=3×4;
…;
n=n时,棋子个数为n×4=4n.
故选:A.
3.【解答】解:由题意得:第一个图形中小正方形的个数为1,
第二个为1+2=3,
第三个为1+2+3=6,
第四个为1+2+3+4=10,
…;
第(11)个图形中小正方形的个数为:1+2+3+4+5+6+7+8+9+10+11=66.
故选:B.
4.【解答】方法一:
解:第一个图形正三角形的个数为5,
第二个图形正三角形的个数为5×3+2=17,
第三个图形正三角形的个数为17×3+2=53,
第四个图形正三角形的个数为53×3+2=161,
故选B.
方法二:
,,,,…,
∴,
(a2﹣a1)+(a3﹣a2)+(a4﹣a3)+…+(an﹣an﹣1)=an﹣a1,
∴an﹣a1=4×(3+32+…+3n﹣1)=4×(3+32+…+3n﹣1)=(用错位相减法可求出)
∴,
∵a1=5,
∴.
故选:B.
5.【解答】解:根据已知图形得:
第1个图形五角星个数:1×3+1,
第2个图形五角星个数:2×3+1,
第3个图形五角星个数:3×3+1,
第4个图形五角星个数:4×3+1,
由此规律得:
第2个图形五角星个数:n×3+1,
故第n个图形中共有3n+1个图形;
A答案为4+3(n﹣1)=3n+1.
故选:A.
6.【解答】解:x2﹣1﹣(1﹣x﹣x2)=x2﹣1﹣1+x+x2=2x2+x﹣2.
故选:A.
7.【解答】解:∵第一幅图中有22+1=5个棋子,
第二幅图中有32+1=10个棋子,
第三幅图中有42+1=17个棋子,
第四幅图中有52+1=26个棋子,
…
∴第n幅图中所含棋子数目为(n+1)2+1,
∴第6幅图中所含棋子数目为49+1=50.
故选:B.
8.【解答】解:原式=5x﹣5x﹣5=﹣5.
故选:A.
9.【解答】解:观察图形可知,阴影部分面积为ab﹣(a﹣c)(b﹣c)=ab﹣ab+ac+bc﹣c2=ac+(b﹣c)c.
故选:C.
10.【解答】解:A、两个矩形的对应角相等,但对应边的比不一定相等,故错误;
B、两个等腰梯形不一定相似,故错误;
C、对应边成比例且对应角相等的两个四边形是全等形,故错误;
D、有一个内角相等的菱形是相似图形,故正确,
故选:D.
二.填空题(共16小题)
11.【解答】解:原式=2x﹣2x+2y=2y,
故答案为:2y
12.【解答】解:根据规律可知
第n个图形有3n个●,
所以第12个图形共有12×3=36个●.
故答案为:36.
13.【解答】解:由题意可得:阴影部分的面积和为:
π(22﹣12)+π(42﹣32)+π(62﹣52)+…+π(202﹣192)+π(222﹣212)
=3π+7π+11π+15π+…+39π+43π
=(3π+43π)×11÷2
=253π.
故答案为:253π.
14.【解答】解:观察第二个图形,有3个四边形,1+3=4(个)正六边形,
第三个图形,有6个四边形,1+3+3=7(个)正六边形
依此类推,
第n个图形中,有3(n﹣1)个四边形,1+3(n﹣1)=(3n﹣2)个正六边形.
∴第18个图中,
共有3×(18﹣1)=51(个)四边形,共有3×18﹣2=52(个)正六边形.
故答案为:51,52.
15.【解答】解:一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,从出发到第1次回到点A共爬行了8cm,
而2015=251×8+7,
所以当电子甲虫爬行2015cm时停下,它停的位置是G点.
故点G.
16.【解答】解:另一边的长为:(2a+b)+(a﹣b)=3a.
∴周长为[(2a+b)+3a]×2=10a+2b.
17.【解答】解:第一个图需棋子3+1=4;
第二个图需棋子3×2+1=7;
第三个图需棋子3×3+1=10;
第四个图需棋子3×4+1=13;
第五个图需棋子3×5+1=16;
…
第n个图需棋子3n+1枚.
故答案为:16,3n+1.
18.【解答】解:第1个图案是由2个组成:
即为:2=1×2;
第2个图案是由9个组成:
即为:9=3×3;
第3个图案是由5×4=20个组成:
即为:20=5×4;
第4个图案是由35个组成:
即为:35=7×5;
以此类推:第n个图案的个数:(2n﹣1)(n+1).
故答案为:(2n﹣1)(n+1).
19.【解答】解:设线段有n个点,分成的线段有m条,有以下规律:
n个m条
2 1
3 1+2
4 1+2+3
:
:
:
n m=1+…+(n﹣1)=
10个点把线段AB共分成=45条.
20.【解答】解:通过图形变化可知:
n=1时 火柴棒总数为 3×1
n=2时 火柴棒总数为 3×(1+2),
n=3时 火柴棒总数为 3(1+2+3),
∴n=10时 火柴棒总数为 3×(1+2+3+…+9+10)
故答案为165
21.【解答】解:第1个图形需要木棒4=1+3×1根,硬币2=2×1枚;
第2个图形需要木棒7=1+3×2根,硬币4=2×2枚;
第3个图形需要木棒10=1+3×3根,硬币6=2×3枚;
…
则第n个图形需要木棒数为:1+3n,硬币:2n.
故答案为:(3n+1),2n.
22.【解答】解:第①个图形中五角星的个数为2=2×12;
第②个图形中五角星的个数为2+4+2=8=2×4=2×22;
第③个图形中五角星的个数为2+4+6+4+2=18=2×32;
第④个图形中五角星的个数为2×42;
所以第⑥个图形中五角星的个数为2×62=2×36=72.
故答案为72.
23.【解答】解:“上”字共有四个端点每次每个端点增加一枚棋子,而初始时内部有两枚棋子不发生变化,
所以第n个字需要4n+2枚棋子.
故答案为:4n+2.
24.【解答】解:第一个图中钢管数为1+2=3;
第二个图中钢管数为2+3+4=9;
第三个图中钢管数为3+4+5+6=18;
第四个图中钢管数为4+5+6+7+8=30,
依此类推,第n个图中钢管数为n+(n+1)+(n+2)+…+2n=+=n2+n,
故答案为:n2+n.
25.【解答】解:第一次操作后余下的线段之和为1﹣,
第二次操作后余下的线段之和为(1﹣)2,
…
第n次操作后余下的线段之和为(1﹣)n=,
则被取走的所有线段长度之和为1﹣.
故答案为:1﹣.
26.【解答】解:结合图形,发现:
第n(n是正整数)个图形需要黑色棋子的个数是n(n+2)=n2+2n(个).
三.解答题(共3小题)
27.【解答】解:原式=3a2b+2a2b+6ab﹣4a2b﹣4ab﹣3ab=a2b﹣ab,
当a=3,b=﹣时,原式=﹣3+1=﹣2.
28.【解答】(1)如图:
;
(2)
分割次数(n) 1 2 3 …
正六边形的面积S …
;
(3).
29.【解答】解:(1)观察以上图形,图④中所用火柴棒的根数为9,
猜想:在图n中,所用火柴棒的根数为2n+1(用n表示);
(2)将图n放在直角坐标系中,设其中第一个基本图形的中心O1的坐标为(,y1),O2的坐标为(2,2),O3的坐标为(3,1),O4的坐标为(4,2),…O2014的坐标为(2014,2).
故答案为:(1)9;2n+1;(2)1;(2014,2).
