第4章 圆和扇形 单元试卷(含解析)2023-2024学年沪教版(上海)六年级数学第一学期
文档属性
| 名称 | 第4章 圆和扇形 单元试卷(含解析)2023-2024学年沪教版(上海)六年级数学第一学期 |

|
|
| 格式 | docx | ||
| 文件大小 | 319.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 00:00:00 | ||
图片预览



文档简介
沪教新版六年级(上)单元试卷:第4章 圆和扇形
一、选择题(共13小题)
1.如图,用两根等长的金属丝,各自首尾相接,分别围成正方形ABCD和扇形A1D1C1,使A1D1=AD,D1C1=DC,正方形面积为P,扇形面积为Q,那么P和Q的关系是( )
A.P<Q B.P=Q C.P>Q D.无法确定
2.如图,AB为半圆的直径,且AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )
A.π B.2π C. D.4π
3.如图,已知扇形的圆心角为60°,半径为,则图中弓形的面积为( )
A. B. C. D.
4.如图,在正方形ABCD中,对角线BD的长为.若将BD绕点B旋转后,点D落在BC延长线上的点D′处,点D经过的路径为,则图中阴影部分的面积是( )
A.﹣1 B.﹣ C.﹣ D.π﹣2
5.如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是( )
A.π﹣1 B.π﹣2 C.π﹣2 D.π﹣1
6.如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心,ED为半径作半圆,交A、B所在的直线于M、N两点,分别以直径MD、ND为直径作半圆,则阴影部分面积为( )
A.9 B.18 C.36 D.72
7.如图,已知⊙O的周长为4π,的长为π,则图中阴影部分的面积为( )
A.π﹣2 B.π﹣ C.π D.2
8.如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2,则S阴影=( )
A.π B.2π C. D.π
9.如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为( )
A. B. C. D.
10.如图,半径为2cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为( )
A.(﹣1)cm2 B.(+1)cm2 C.1cm2 D.cm2
11.在圆心角为120°的扇形AOB中,半径OA=6cm,则扇形OAB的面积是( )
A.6πcm2 B.8πcm2 C.12πcm2 D.24πcm2
12.如图,三个小正方形的边长都为1,则图中阴影部分面积的和是( )
A. B. C. D.
13.如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为( )
A.﹣ B.﹣2 C.π﹣ D.﹣
二、填空题(共17小题)
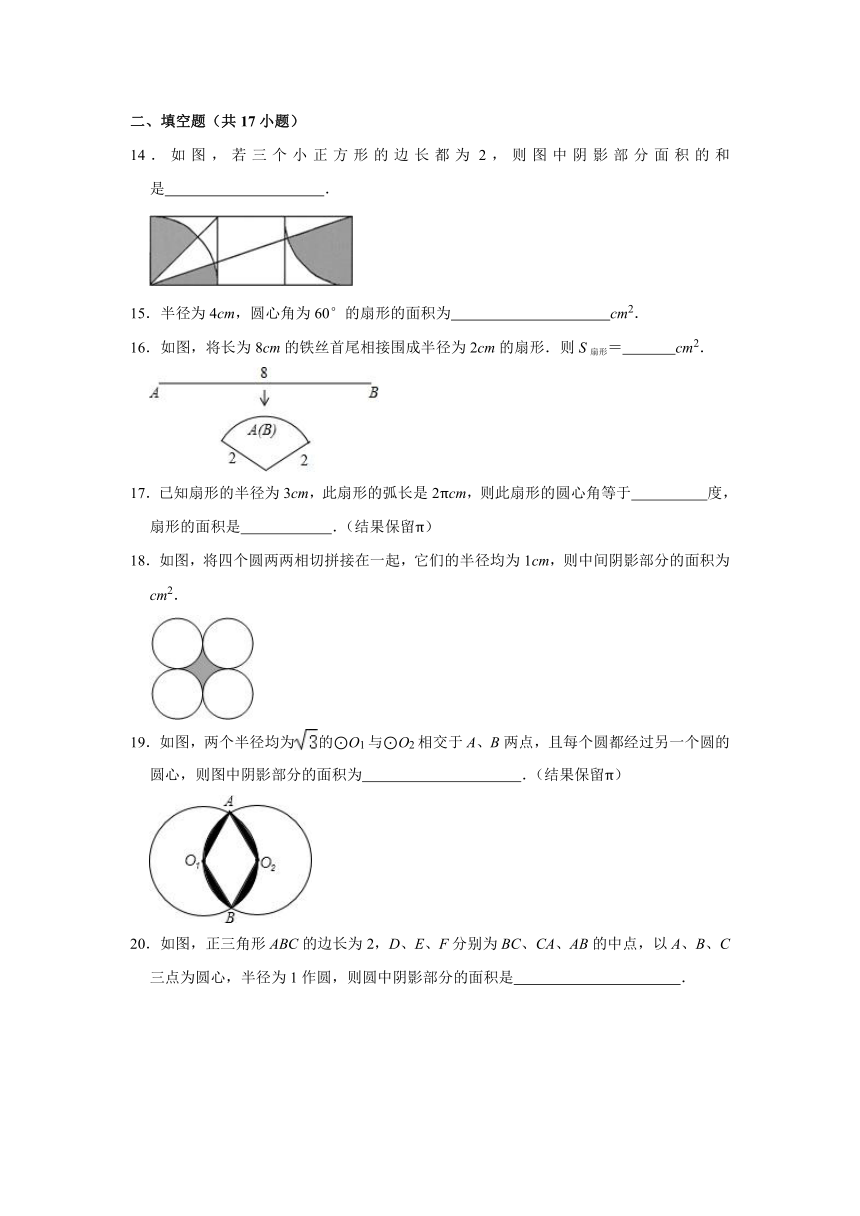
14.如图,若三个小正方形的边长都为2,则图中阴影部分面积的和是 .
15.半径为4cm,圆心角为60°的扇形的面积为 cm2.
16.如图,将长为8cm的铁丝首尾相接围成半径为2cm的扇形.则S扇形= cm2.
17.已知扇形的半径为3cm,此扇形的弧长是2πcm,则此扇形的圆心角等于 度,扇形的面积是 .(结果保留π)
18.如图,将四个圆两两相切拼接在一起,它们的半径均为1cm,则中间阴影部分的面积为 cm2.
19.如图,两个半径均为的⊙O1与⊙O2相交于A、B两点,且每个圆都经过另一个圆的圆心,则图中阴影部分的面积为 .(结果保留π)
20.如图,正三角形ABC的边长为2,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心,半径为1作圆,则圆中阴影部分的面积是 .
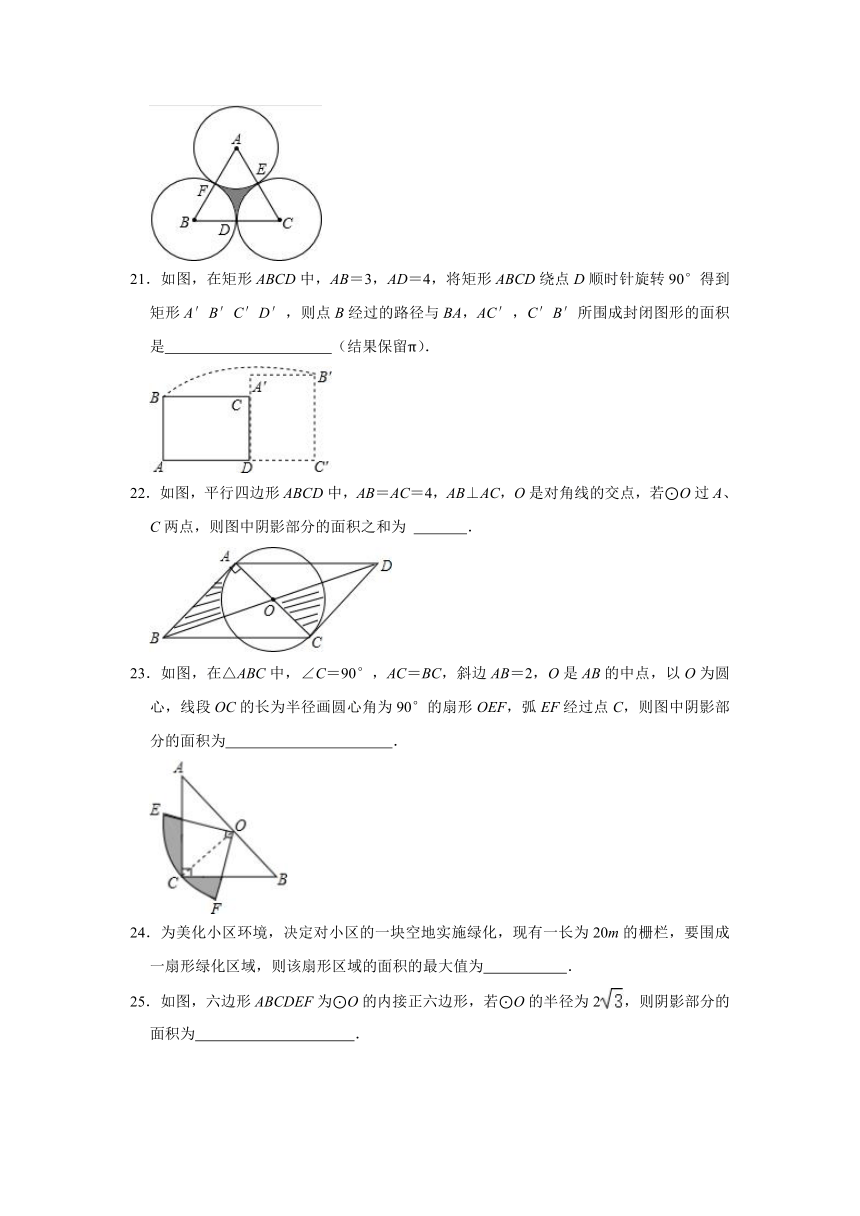
21.如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是 (结果保留π).
22.如图,平行四边形ABCD中,AB=AC=4,AB⊥AC,O是对角线的交点,若⊙O过A、C两点,则图中阴影部分的面积之和为 .
23.如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为 .
24.为美化小区环境,决定对小区的一块空地实施绿化,现有一长为20m的栅栏,要围成一扇形绿化区域,则该扇形区域的面积的最大值为 .
25.如图,六边形ABCDEF为⊙O的内接正六边形,若⊙O的半径为2,则阴影部分的面积为 .
26.如图,某实践小组要在广场一角的扇形区域内种植红、黄两种花,半径OA=4米,C是OA的中点,点D在上,CD∥OB,则图中种植黄花(即阴影部分)的面积是 (结果保留π).
27.一个扇形的圆心角为120°,半径为3,则这个扇形的面积为 (结果保留π)
28.如图,在 ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是 (结果保留π).
29.如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为 cm2.
30.如图,三个小正方形的边长都为1,则图中阴影部分面积的和是 (结果保留π).
沪教新版六年级(上)单元试卷:第4章 圆和扇形
参考答案与试题解析
一、选择题(共13小题)
1.【解答】解:正方形面积P=AB2,扇形面积Q=lr=×2AB AB=AB2,
其中l为扇形弧长,等于正方形2个边长,r为扇形半径,等于正方形边长,
则P=Q.
故选:B.
2.【解答】解:∵S阴影=S扇形ABA′+S半圆﹣S半圆
=S扇形ABA′
=
=2π.
故选:B.
3.【解答】解:过A作AD⊥CB,
∵∠CAB=60°,AC=AB,
∴△ABC是等边三角形,
∵AC=,
∴AD=AC sin60°=×=,
∴△ABC面积:=,
∵扇形面积:=,
∴弓形的面积为:﹣=,
故选:C.
4.【解答】解:∵四边形ABCD是正方形,
∴∠DBD′=45°,BC=CD,
∵BD的长为,
∴BC=CD=1,
∴S扇形BDD′==,
S△CBD=1×1=,
∴阴影部分的面积:﹣.
故选:C.
5.【解答】解:在Rt△ACB中,AB==2,
∵BC是半圆的直径,
∴∠CDB=90°,
在等腰Rt△ACB中,CD垂直平分AB,CD=BD=,
∴D为半圆的中点,
∴S阴影部分=S扇形ACB﹣S△ADC=π×22﹣×()2=π﹣1.
故选:D.
6.【解答】解:根据图形可知阴影部分的面积=两个小的半圆的面积+△DMN的面积﹣大半圆的面积.
∵MN是半圆的直径,
∴∠MDN=90°.
在Rt△MDN中,MN2=MD2+DN2,
∴两个小半圆的面积=大半圆的面积.
∴阴影部分的面积=△DMN的面积.
在Rt△AED中,DE===3,
∴阴影部分的面积=△DMN的面积==.
故选:B.
7.【解答】解:∵⊙O的周长为4π,
∴⊙O的半径是r=4π÷2π=2,
∵的长为π,
∴的长等于⊙O的周长的,
∴∠AOB=90°,
∴S阴影==π﹣2.
故选:A.
8.【解答】解:如图,CD⊥AB,交AB于点E,
∵AB是直径,
∴CE=DE=CD=,
又∵∠CDB=30°
∴∠COE=60°,
∴OE=1,OC=2,
∴BE=1,
∴S△BED=S△OEC,
∴S阴影=S扇形BOC==.
故选:D.
9.【解答】解:连接CD,作DM⊥BC,DN⊥AC.
∵CA=CB,∠ACB=90°,点D为AB的中点,
∴DC=AB=1,四边形DMCN是正方形,DM=.
则扇形FDE的面积是:=.
∵CA=CB,∠ACB=90°,点D为AB的中点,
∴CD平分∠BCA,
又∵DM⊥BC,DN⊥AC,
∴DM=DN,
∵∠GDH=∠MDN=90°,
∴∠GDM=∠HDN,
则在△DMG和△DNH中,
,
∴△DMG≌△DNH(ASA),
∴S四边形DGCH=S四边形DMCN=.
则阴影部分的面积是:﹣.
故选:D.
10.【解答】解:方法一:∵扇形OAB的圆心角为90°,扇形半径为2,
∴扇形面积为:=π(cm2),
半圆面积为:×π×12=(cm2),
∴SQ+SM=SM+SP=(cm2),
∴SQ=SP,
连接AB,OD,
∵两半圆的直径相等,
∴∠AOD=∠BOD=45°,
∴S绿色=S△AOD=×2×1=1(cm2),
∴阴影部分Q的面积为:S扇形AOB﹣S半圆﹣S绿色=π﹣﹣1=﹣1(cm2).
方法二:记这两个半圆的圆心分别为点E,点F,这两个半圆的交点为G,连接EG,FG,
则FG=FD=EO=EG,
又∠AOB=90°,
∴四边形OEGF为正方形,
∴S阴影=S扇形AOB﹣S正方形OEGF﹣2S扇形GEA=×π×22﹣12﹣2××π×12
=﹣1.
故选:A.
11.【解答】解:∵在圆心角为120°的扇形AOB中,半径OA=6cm,
∴扇形OAB的面积是:=12π(cm2),
故选:C.
12.【解答】解:
∵四边形都是正方形,
∴边长都等于1,∠EHG=90°,∠ABD=∠ABC=45°,
∵如图(II)和(IIII)的面积相等,
∴把图形(II)补到图形(IIII)上,
∴图中阴影部分的面积S=+×=,
故选:B.
13.【解答】解:过O点作OE⊥CD于E,
∵AB为⊙O的切线,
∴∠ABO=90°,
∵∠A=30°,
∴∠AOB=60°,
∴∠COD=120°,∠OCD=∠ODC=30°,
∵⊙O的半径为2,
∴OE=1,CE=DE=,
∴CD=2,
∴图中阴影部分的面积为:﹣×2×1=π﹣.
故选:A.
二、填空题(共17小题)
14.【解答】解:如图,由题意得:
∠MPN=45°,∠AOB=90°;
由正方形的对称性知:
图中阴影部分面积的和=S扇形MPN+S扇形AOB
==,
故答案为.
15.【解答】解:半径为4cm,圆心角为60°的扇形的面积为:=π(cm2).
故答案为:π.
16.【解答】解:由题意知,弧长=8﹣2×2=4cm,
扇形的面积是×4×2=4cm2,
故答案为:4.
17.【解答】解:设扇形的圆心角的度数是n°,则
=2π,
解得:n=120,
扇形的面积是:=3π(cm2).
故答案为:120,3πcm2.
18.【解答】解:∵半径为1cm的四个圆两两相切,
∴四边形是边长为2cm的正方形,圆的面积为πcm2,
阴影部分的面积=2×2﹣π=4﹣π(cm2),
故答案为:4﹣π.
19.【解答】解:连接O1O2,过点O1作O1C⊥AO2于点C,
由题意可得:AO1=O1O2=AO2=,
∴△AO1O2是等边三角形,
∴CO1=O1O2sin60°=,
∴S=××=,
==,
∴=﹣S=﹣,
∴图中阴影部分的面积为:4(﹣)=2π﹣3.
故答案为:2π﹣3.
20.【解答】解:连接AD.
∵△ABC是正三角形,BD=CD=1,
∴∠BAC=∠B=∠C=60°,AD⊥BC.
∴AD=.
∴阴影部分的面积=×2×﹣3×=﹣.
故答案为:﹣.
21.【解答】解:如图,连接BD与B′D,
点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是:
S扇形BDB′+S矩形ABCD=π×52+3×4=+12.
故答案为:+12.
22.【解答】解:∵∠AOB=∠COD,
∴S阴影=S△AOB.
∵四边形ABCD是平行四边形,
∴OA=AC=×4=2.
∵AB⊥AC,
∴S阴影=S△AOB=OA AB=×2×4=4.
故答案为:4.
23.【解答】解:连接OC,作OM⊥BC,ON⊥AC.
∵CA=CB,∠ACB=90°,点O为AB的中点,
∴OC=AB=1,四边形OMCN是正方形,OM=.
则扇形FOE的面积是:=.
∵OA=OB,∠ACB=90°,点O为AB的中点,
∴OC平分∠BCA,
又∵OM⊥BC,ON⊥AC,
∴OM=ON,
∵∠GOH=∠MON=90°,
∴∠GOM=∠HON,
则在△OMG和△ONH中,
,
∴△OMG≌△ONH(AAS),
∴S四边形OGCH=S四边形OMCN=()2=.
则阴影部分的面积是:﹣.
故答案为:﹣.
24.【解答】解:设扇形区域的半径为xm,则扇形的弧长为(20﹣2x)m,该扇形区域的面积为ym2,
则y=x(20﹣2x)=﹣x2+10x=﹣(x﹣5)2+25,
∴该扇形区域的面积的最大值为25m2.
故答案为:25m2.
25.【解答】解:∵圆的半径为2,
∴面积为12π,
∵空白正六边形为六个边长为2的正三角形,
∴每个三角形面积为×2××sin60°=3,
∴正六边形面积为18,
∴阴影面积为(12π﹣18)×=2,
故答案为:2.
26.【解答】解:连接OD,
∵C是OA的中点,OA=OD,
∴OC=OD=2,CD=2,
∴∠ODC=30°,则∠DOA=60°,
种植黄花(即阴影部分)的面积=扇形AOD的面积﹣△DOC的面积
=﹣×2×2
=π﹣2,
故答案为:π﹣2.
27.【解答】解:由题意得,n=120°,R=3,
故S扇形===3π.
故答案为:3π.
28.【解答】解:过D点作DF⊥AB于点F.
∵AD=2,AB=4,∠A=30°,
∴DF=AD sin30°=1,EB=AB﹣AE=2,
∴阴影部分的面积:
4×1﹣﹣2×1÷2
=4﹣π﹣1
=3﹣π.
故答案为:3﹣π.
29.【解答】解:连接OC,过C点作CF⊥OA于F,
∵半径OA=2cm,C为的中点,D、E分别是OA、OB的中点,
∴OD=OE=1cm,OC=2cm,∠AOC=45°,
∴CF=,
∴空白图形ACD的面积=扇形OAC的面积﹣三角形OCD的面积
=﹣×
=π﹣(cm2)
三角形ODE的面积=OD×OE=(cm2),
∴图中阴影部分的面积=扇形OAB的面积﹣空白图形ACD的面积﹣三角形ODE的面积
=﹣(π﹣)﹣
=π+﹣(cm2).
故图中阴影部分的面积为(π+﹣)cm2.
故答案为:(π+﹣).
30.【解答】解:根据图示知,∠1+∠2=180°﹣90°﹣45°=45°,
∵∠ABC+∠ADC=180°,
∴图中阴影部分的圆心角的和是90°+90°﹣∠1﹣∠2=135°,
∴阴影部分的面积应为:S==.
故答案为:.
一、选择题(共13小题)
1.如图,用两根等长的金属丝,各自首尾相接,分别围成正方形ABCD和扇形A1D1C1,使A1D1=AD,D1C1=DC,正方形面积为P,扇形面积为Q,那么P和Q的关系是( )
A.P<Q B.P=Q C.P>Q D.无法确定
2.如图,AB为半圆的直径,且AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )
A.π B.2π C. D.4π
3.如图,已知扇形的圆心角为60°,半径为,则图中弓形的面积为( )
A. B. C. D.
4.如图,在正方形ABCD中,对角线BD的长为.若将BD绕点B旋转后,点D落在BC延长线上的点D′处,点D经过的路径为,则图中阴影部分的面积是( )
A.﹣1 B.﹣ C.﹣ D.π﹣2
5.如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是( )
A.π﹣1 B.π﹣2 C.π﹣2 D.π﹣1
6.如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心,ED为半径作半圆,交A、B所在的直线于M、N两点,分别以直径MD、ND为直径作半圆,则阴影部分面积为( )
A.9 B.18 C.36 D.72
7.如图,已知⊙O的周长为4π,的长为π,则图中阴影部分的面积为( )
A.π﹣2 B.π﹣ C.π D.2
8.如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2,则S阴影=( )
A.π B.2π C. D.π
9.如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为( )
A. B. C. D.
10.如图,半径为2cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为( )
A.(﹣1)cm2 B.(+1)cm2 C.1cm2 D.cm2
11.在圆心角为120°的扇形AOB中,半径OA=6cm,则扇形OAB的面积是( )
A.6πcm2 B.8πcm2 C.12πcm2 D.24πcm2
12.如图,三个小正方形的边长都为1,则图中阴影部分面积的和是( )
A. B. C. D.
13.如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为( )
A.﹣ B.﹣2 C.π﹣ D.﹣
二、填空题(共17小题)
14.如图,若三个小正方形的边长都为2,则图中阴影部分面积的和是 .
15.半径为4cm,圆心角为60°的扇形的面积为 cm2.
16.如图,将长为8cm的铁丝首尾相接围成半径为2cm的扇形.则S扇形= cm2.
17.已知扇形的半径为3cm,此扇形的弧长是2πcm,则此扇形的圆心角等于 度,扇形的面积是 .(结果保留π)
18.如图,将四个圆两两相切拼接在一起,它们的半径均为1cm,则中间阴影部分的面积为 cm2.
19.如图,两个半径均为的⊙O1与⊙O2相交于A、B两点,且每个圆都经过另一个圆的圆心,则图中阴影部分的面积为 .(结果保留π)
20.如图,正三角形ABC的边长为2,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心,半径为1作圆,则圆中阴影部分的面积是 .
21.如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是 (结果保留π).
22.如图,平行四边形ABCD中,AB=AC=4,AB⊥AC,O是对角线的交点,若⊙O过A、C两点,则图中阴影部分的面积之和为 .
23.如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为 .
24.为美化小区环境,决定对小区的一块空地实施绿化,现有一长为20m的栅栏,要围成一扇形绿化区域,则该扇形区域的面积的最大值为 .
25.如图,六边形ABCDEF为⊙O的内接正六边形,若⊙O的半径为2,则阴影部分的面积为 .
26.如图,某实践小组要在广场一角的扇形区域内种植红、黄两种花,半径OA=4米,C是OA的中点,点D在上,CD∥OB,则图中种植黄花(即阴影部分)的面积是 (结果保留π).
27.一个扇形的圆心角为120°,半径为3,则这个扇形的面积为 (结果保留π)
28.如图,在 ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是 (结果保留π).
29.如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为 cm2.
30.如图,三个小正方形的边长都为1,则图中阴影部分面积的和是 (结果保留π).
沪教新版六年级(上)单元试卷:第4章 圆和扇形
参考答案与试题解析
一、选择题(共13小题)
1.【解答】解:正方形面积P=AB2,扇形面积Q=lr=×2AB AB=AB2,
其中l为扇形弧长,等于正方形2个边长,r为扇形半径,等于正方形边长,
则P=Q.
故选:B.
2.【解答】解:∵S阴影=S扇形ABA′+S半圆﹣S半圆
=S扇形ABA′
=
=2π.
故选:B.
3.【解答】解:过A作AD⊥CB,
∵∠CAB=60°,AC=AB,
∴△ABC是等边三角形,
∵AC=,
∴AD=AC sin60°=×=,
∴△ABC面积:=,
∵扇形面积:=,
∴弓形的面积为:﹣=,
故选:C.
4.【解答】解:∵四边形ABCD是正方形,
∴∠DBD′=45°,BC=CD,
∵BD的长为,
∴BC=CD=1,
∴S扇形BDD′==,
S△CBD=1×1=,
∴阴影部分的面积:﹣.
故选:C.
5.【解答】解:在Rt△ACB中,AB==2,
∵BC是半圆的直径,
∴∠CDB=90°,
在等腰Rt△ACB中,CD垂直平分AB,CD=BD=,
∴D为半圆的中点,
∴S阴影部分=S扇形ACB﹣S△ADC=π×22﹣×()2=π﹣1.
故选:D.
6.【解答】解:根据图形可知阴影部分的面积=两个小的半圆的面积+△DMN的面积﹣大半圆的面积.
∵MN是半圆的直径,
∴∠MDN=90°.
在Rt△MDN中,MN2=MD2+DN2,
∴两个小半圆的面积=大半圆的面积.
∴阴影部分的面积=△DMN的面积.
在Rt△AED中,DE===3,
∴阴影部分的面积=△DMN的面积==.
故选:B.
7.【解答】解:∵⊙O的周长为4π,
∴⊙O的半径是r=4π÷2π=2,
∵的长为π,
∴的长等于⊙O的周长的,
∴∠AOB=90°,
∴S阴影==π﹣2.
故选:A.
8.【解答】解:如图,CD⊥AB,交AB于点E,
∵AB是直径,
∴CE=DE=CD=,
又∵∠CDB=30°
∴∠COE=60°,
∴OE=1,OC=2,
∴BE=1,
∴S△BED=S△OEC,
∴S阴影=S扇形BOC==.
故选:D.
9.【解答】解:连接CD,作DM⊥BC,DN⊥AC.
∵CA=CB,∠ACB=90°,点D为AB的中点,
∴DC=AB=1,四边形DMCN是正方形,DM=.
则扇形FDE的面积是:=.
∵CA=CB,∠ACB=90°,点D为AB的中点,
∴CD平分∠BCA,
又∵DM⊥BC,DN⊥AC,
∴DM=DN,
∵∠GDH=∠MDN=90°,
∴∠GDM=∠HDN,
则在△DMG和△DNH中,
,
∴△DMG≌△DNH(ASA),
∴S四边形DGCH=S四边形DMCN=.
则阴影部分的面积是:﹣.
故选:D.
10.【解答】解:方法一:∵扇形OAB的圆心角为90°,扇形半径为2,
∴扇形面积为:=π(cm2),
半圆面积为:×π×12=(cm2),
∴SQ+SM=SM+SP=(cm2),
∴SQ=SP,
连接AB,OD,
∵两半圆的直径相等,
∴∠AOD=∠BOD=45°,
∴S绿色=S△AOD=×2×1=1(cm2),
∴阴影部分Q的面积为:S扇形AOB﹣S半圆﹣S绿色=π﹣﹣1=﹣1(cm2).
方法二:记这两个半圆的圆心分别为点E,点F,这两个半圆的交点为G,连接EG,FG,
则FG=FD=EO=EG,
又∠AOB=90°,
∴四边形OEGF为正方形,
∴S阴影=S扇形AOB﹣S正方形OEGF﹣2S扇形GEA=×π×22﹣12﹣2××π×12
=﹣1.
故选:A.
11.【解答】解:∵在圆心角为120°的扇形AOB中,半径OA=6cm,
∴扇形OAB的面积是:=12π(cm2),
故选:C.
12.【解答】解:
∵四边形都是正方形,
∴边长都等于1,∠EHG=90°,∠ABD=∠ABC=45°,
∵如图(II)和(IIII)的面积相等,
∴把图形(II)补到图形(IIII)上,
∴图中阴影部分的面积S=+×=,
故选:B.
13.【解答】解:过O点作OE⊥CD于E,
∵AB为⊙O的切线,
∴∠ABO=90°,
∵∠A=30°,
∴∠AOB=60°,
∴∠COD=120°,∠OCD=∠ODC=30°,
∵⊙O的半径为2,
∴OE=1,CE=DE=,
∴CD=2,
∴图中阴影部分的面积为:﹣×2×1=π﹣.
故选:A.
二、填空题(共17小题)
14.【解答】解:如图,由题意得:
∠MPN=45°,∠AOB=90°;
由正方形的对称性知:
图中阴影部分面积的和=S扇形MPN+S扇形AOB
==,
故答案为.
15.【解答】解:半径为4cm,圆心角为60°的扇形的面积为:=π(cm2).
故答案为:π.
16.【解答】解:由题意知,弧长=8﹣2×2=4cm,
扇形的面积是×4×2=4cm2,
故答案为:4.
17.【解答】解:设扇形的圆心角的度数是n°,则
=2π,
解得:n=120,
扇形的面积是:=3π(cm2).
故答案为:120,3πcm2.
18.【解答】解:∵半径为1cm的四个圆两两相切,
∴四边形是边长为2cm的正方形,圆的面积为πcm2,
阴影部分的面积=2×2﹣π=4﹣π(cm2),
故答案为:4﹣π.
19.【解答】解:连接O1O2,过点O1作O1C⊥AO2于点C,
由题意可得:AO1=O1O2=AO2=,
∴△AO1O2是等边三角形,
∴CO1=O1O2sin60°=,
∴S=××=,
==,
∴=﹣S=﹣,
∴图中阴影部分的面积为:4(﹣)=2π﹣3.
故答案为:2π﹣3.
20.【解答】解:连接AD.
∵△ABC是正三角形,BD=CD=1,
∴∠BAC=∠B=∠C=60°,AD⊥BC.
∴AD=.
∴阴影部分的面积=×2×﹣3×=﹣.
故答案为:﹣.
21.【解答】解:如图,连接BD与B′D,
点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是:
S扇形BDB′+S矩形ABCD=π×52+3×4=+12.
故答案为:+12.
22.【解答】解:∵∠AOB=∠COD,
∴S阴影=S△AOB.
∵四边形ABCD是平行四边形,
∴OA=AC=×4=2.
∵AB⊥AC,
∴S阴影=S△AOB=OA AB=×2×4=4.
故答案为:4.
23.【解答】解:连接OC,作OM⊥BC,ON⊥AC.
∵CA=CB,∠ACB=90°,点O为AB的中点,
∴OC=AB=1,四边形OMCN是正方形,OM=.
则扇形FOE的面积是:=.
∵OA=OB,∠ACB=90°,点O为AB的中点,
∴OC平分∠BCA,
又∵OM⊥BC,ON⊥AC,
∴OM=ON,
∵∠GOH=∠MON=90°,
∴∠GOM=∠HON,
则在△OMG和△ONH中,
,
∴△OMG≌△ONH(AAS),
∴S四边形OGCH=S四边形OMCN=()2=.
则阴影部分的面积是:﹣.
故答案为:﹣.
24.【解答】解:设扇形区域的半径为xm,则扇形的弧长为(20﹣2x)m,该扇形区域的面积为ym2,
则y=x(20﹣2x)=﹣x2+10x=﹣(x﹣5)2+25,
∴该扇形区域的面积的最大值为25m2.
故答案为:25m2.
25.【解答】解:∵圆的半径为2,
∴面积为12π,
∵空白正六边形为六个边长为2的正三角形,
∴每个三角形面积为×2××sin60°=3,
∴正六边形面积为18,
∴阴影面积为(12π﹣18)×=2,
故答案为:2.
26.【解答】解:连接OD,
∵C是OA的中点,OA=OD,
∴OC=OD=2,CD=2,
∴∠ODC=30°,则∠DOA=60°,
种植黄花(即阴影部分)的面积=扇形AOD的面积﹣△DOC的面积
=﹣×2×2
=π﹣2,
故答案为:π﹣2.
27.【解答】解:由题意得,n=120°,R=3,
故S扇形===3π.
故答案为:3π.
28.【解答】解:过D点作DF⊥AB于点F.
∵AD=2,AB=4,∠A=30°,
∴DF=AD sin30°=1,EB=AB﹣AE=2,
∴阴影部分的面积:
4×1﹣﹣2×1÷2
=4﹣π﹣1
=3﹣π.
故答案为:3﹣π.
29.【解答】解:连接OC,过C点作CF⊥OA于F,
∵半径OA=2cm,C为的中点,D、E分别是OA、OB的中点,
∴OD=OE=1cm,OC=2cm,∠AOC=45°,
∴CF=,
∴空白图形ACD的面积=扇形OAC的面积﹣三角形OCD的面积
=﹣×
=π﹣(cm2)
三角形ODE的面积=OD×OE=(cm2),
∴图中阴影部分的面积=扇形OAB的面积﹣空白图形ACD的面积﹣三角形ODE的面积
=﹣(π﹣)﹣
=π+﹣(cm2).
故图中阴影部分的面积为(π+﹣)cm2.
故答案为:(π+﹣).
30.【解答】解:根据图示知,∠1+∠2=180°﹣90°﹣45°=45°,
∵∠ABC+∠ADC=180°,
∴图中阴影部分的圆心角的和是90°+90°﹣∠1﹣∠2=135°,
∴阴影部分的面积应为:S==.
故答案为:.
