第三章 数据的集中趋势和离散程度 小结与思考 课件(共36张PPT) 九年级数学上册苏科版
文档属性
| 名称 | 第三章 数据的集中趋势和离散程度 小结与思考 课件(共36张PPT) 九年级数学上册苏科版 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 19:53:59 | ||
图片预览









文档简介
(共36张PPT)
第3章 · 数据的集中趋势和离散程度
小结与思考
学习目标
1. 整理本章所学知识,构建本章知识框架 ;
2. 进一步理解平均数、众数和中位数的概念,会求一组数据的方差,并在理解概念的基础上,对生活中的某些数据进行分析,做出合理的判断与预测.
s2=[(x1-)2+(x2-)2+…+(xn-)2]
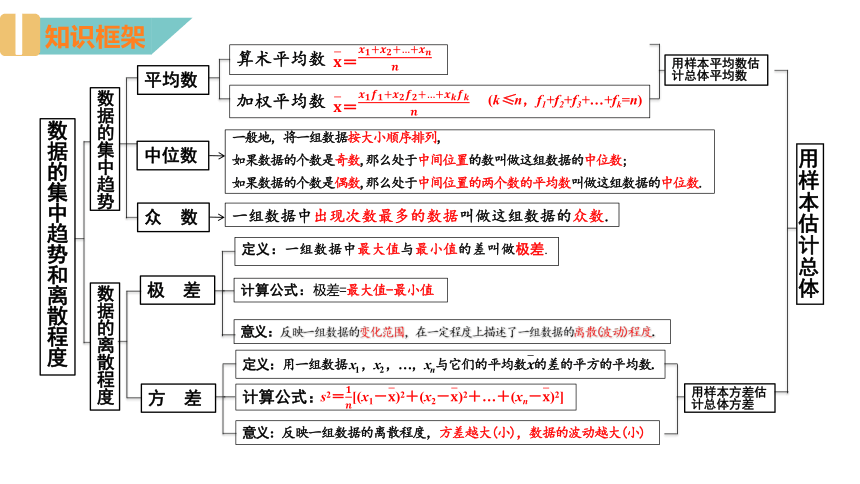
知识框架
数据的集中趋势和离散程度
数据的集中趋势
算术平均数
平均数
加权平均数
中位数
数据的离散程度
极 差
一组数据中出现次数最多的数据叫做这组数据的众数.
定义:一组数据中最大值与最小值的差叫做极差.
方 差
计算公式:极差=最大值-最小值
意义:反映一组数据的变化范围,在一定程度上描述了一组数据的离散(波动)程度.
圆内接四边形的对角互补.
一般地,将一组数据按大小顺序排列,
如果数据的个数是奇数,那么处于中间位置的数叫做这组数据的中位数;
如果数据的个数是偶数,那么处于中间位置的两个数的平均数叫做这组数据的中位数.
众 数
定义:用一组数据 x1 ,x2 ,…,xn 与它们的平均数的差的平方的平均数.
计算公式:
意义:反映一组数据的离散程度,方差越大(小),数据的波动越大(小)
=
=
(k≤n,f1+f2+f3+…+fk=n)
用样本平均数估计总体平均数
用样本方差估计总体方差
用样本估计总体
考点分析
考点一 平均数的计算及应用
例(2022·江苏盐城)合理的膳食可以保证青少年体格和智力的正常发育.综合实践小组为了解某校学生膳食营养状况,从该校1380名学生中调查了100名学生的膳食情况,调查数据整理如下:
中国营养学会推荐的三大营养素供能比参考值 蛋白质 10%~15%
脂肪 20%~30%
碳水化合物 50%~65%
注:供能比为某物质提供的能量占人体所需总能量的百分比.
考点分析
(1)本次调查采用___________的调查方法;(填“普查”或“抽样调查”)
(2)通过对调查数据的计算,样本中的蛋白质平均供能比约为14.6%,请计算样本中的脂肪平均供能比和碳水化合物平均供能比;
抽样调查
解:样本中所有学生的脂肪平均供能比为:
样本中所有学生的碳水化合物平均供能比为:
答:样本中的脂肪平均供能比为38.59%,碳水化合物平均供能比为46.825%.
考点分析
(3)结合以上的调查和计算,对照下表中的参考值,请你针对该校学生膳食状况存在的问题提一条建议.
解:(3)该校学生蛋白质平均供能比在合理的范围内,脂肪平均供能比高于参考值,碳水化合物供能比低于参考值,膳食不合理,营养搭配不均衡,建议增加碳水化合物的摄入量,减少脂肪的摄入量.(答案不唯一,建议合理即可)
巩固练习
1. (2020·江苏淮安) 已知一组数据1、3,a、10的平均数为5,则a=____.
6
2. (2023·湖南)某校组织青年教师教学竞赛活动,包含教学设计和现场教学展示两个方面.其中教学设计占20%,现场展示占80%.某参赛教师的教学设计90分,现场展示95分,则她的最后得分为______.
解:依题意,她的最后得分为:
90×20%+95×80%=94分
94
巩固练习
3.(2022·江苏泰州)学校要从王静,李玉两同学中选拔一人参加运动会志愿者工作,选拔项目为普通话,体育知识和旅游知识.并将成绩依次按4∶3∶3计分. 两人的各项选拔成绩如下表所示,则最终胜出的同学是_______.
∵81分>80分,
∴最终胜出的同学是李玉.
解:王静得分:
李玉得分:
普通话 体育知识 旅游知识
王静 80 90 70
李玉 90 80 70
李玉
4. (2022·江苏徐州) 如图,下列装在相同的透明密封盒内的古钱币,其密封盒上分别标有古钱币的尺寸及质量,例如:钱币“文星高照”密封盒上所标“45.4*2.8mm,24.4g”是指该枚古钱币的直径为45.4mm,厚度为2.8mm,质量为24.4g.已知这些古钱币的材质相同.
巩固练习
由于古钱币无法从密封盒内取出,为判断密封盒上所标古钱币的质量是否有错,桐桐用电子秤测得每枚古钱币与其密封盒的总质量如下:
名称 文星高照 状元及第 鹿鹤同春 顺风大吉 连中三元
总质量/g 58.7 58.1 55.2 54.3 55.8
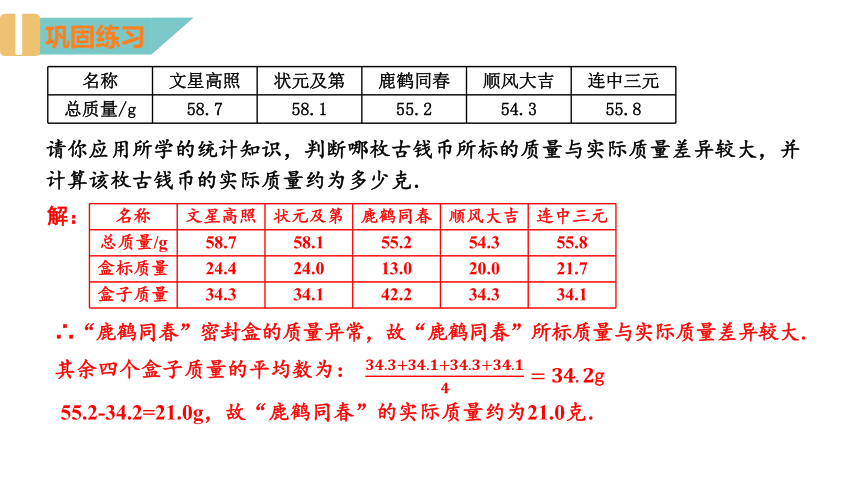
请你应用所学的统计知识,判断哪枚古钱币所标的质量与实际质量差异较大,并计算该枚古钱币的实际质量约为多少克.
名称 文星高照 状元及第 鹿鹤同春 顺风大吉 连中三元
总质量/g 58.7 58.1 55.2 54.3 55.8
盒标质量 24.4 24.0 13.0 20.0 21.7
盒子质量 34.3 34.1 42.2 34.3 34.1
解:
∴“鹿鹤同春”密封盒的质量异常,故“鹿鹤同春”所标质量与实际质量差异较大.
其余四个盒子质量的平均数为:
g
55.2-34.2=21.0g,故“鹿鹤同春”的实际质量约为21.0克.
巩固练习
考点二 中位数和众数的计算及应用
考点分析
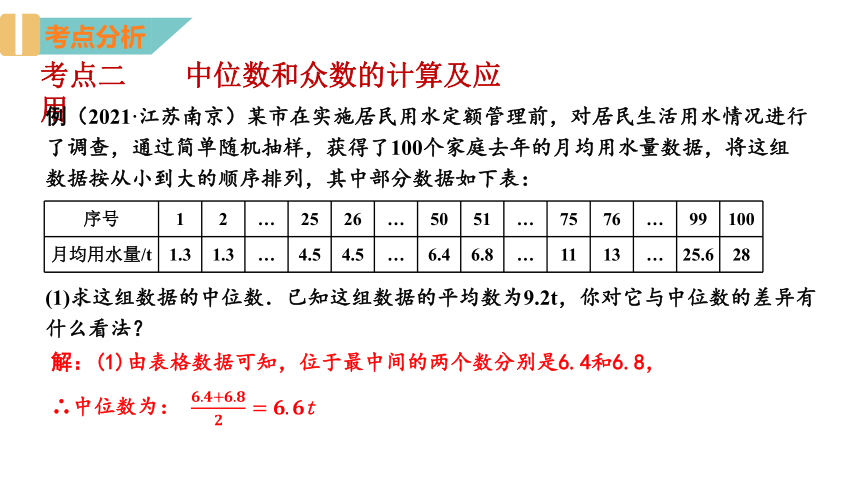
例(2021·江苏南京)某市在实施居民用水定额管理前,对居民生活用水情况进行了调查,通过简单随机抽样,获得了100个家庭去年的月均用水量数据,将这组数据按从小到大的顺序排列,其中部分数据如下表:
序号 1 2 … 25 26 … 50 51 … 75 76 … 99 100
月均用水量/t 1.3 1.3 … 4.5 4.5 … 6.4 6.8 … 11 13 … 25.6 28
(1)求这组数据的中位数.已知这组数据的平均数为9.2t,你对它与中位数的差异有什么看法?
解:(1)由表格数据可知,位于最中间的两个数分别是6.4和6.8,
t
∴中位数为:
考点分析
而这组数据的平均数为9.2t,它们之间差异较大,主要是因为它们各自的特点决定的,主要原因如下:①因为平均数与每一个数据都有关,其中任何数据的变动都会相应引起平均数的变动;主要缺点是易受极端值的影响,这里的极端值是指偏大或偏小数,当出现偏大数时,平均数将会被抬高,当出现偏小数时,平均数会降低;②中位数将数据按照从小到大或从大到小的顺序排列,如果数据个数是奇数,则处于最中间位置的数就是这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数是这组数据的中位数,它的求出不需或只需简单的计算,它不受极端值的影响.这100个数据中,最大的数据是28,最小的是1.3,因此平均数受到极端值的影响,造成与中位数差异较大.
考点分析
(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使75%的家庭水费支出不受影响,你觉得这个标准应该定为多少?
(2)因为第75户用数量为11t,第76户用数量为13t,因此标准应定为11≤a<13(其中 a为标准用水量,单位:t).
为了鼓励节约用水则标准应定为11t.
巩固练习
1. (2023·江苏徐州) 徐州云龙山共九节,蜿蜒起伏,形似游龙,每节山的海拔如图所示.
其中,海拔为中位数的是( )
A.第五节山 B.第六节山 C.第八节山 D.第九节山
C
2. (2023·江苏泰州) 七(1)班40名同学上周家务劳动时间的频数分布直方图如图所示,设这组数据的中位数为mh,则m_____2.6(填“>”“=“<”)
解:因为有40个数据,中位数应是数据有小到大排
列第20、21个数据的平均数,由频数分布直方图可知:第1-5组的人数分别为5,7,12,9,7,
所以第20、21个数据都在第3组,即2.0-2.5,这两个数的平均数一定小于2.6.
<
巩固练习
30
巩固练习
3.(2022·江苏淮安)某公司对25名营销人员4月份销售某种商品的情况统计如下:
销售量(件) 60 50 40 35 30 20
人数 1 4 4 6 7 3
则这25名营销人员销售量的众数是_________.
巩固练习
4. (2022·江苏南通)为了了解八年级学生本学期参加社会实践活动的天数情况,A、B两个县区分别随机抽查了200名八年级学生.根据调查结果绘制了统计图表,部分图表如下:
A、B两个县区的统计表
平均数 众数 中位数
A县区 3.85 3 3
B县区 3.85 4 2.5
(1)若A县区八年级共有约5000名学生,估计该县区八年级学生参加社会实践活动不少于3天的学生约为______名;
(1) 解:根据A县区统计图得,该县区八年级学生参加社会实践活动不少于3天的比例为:30%+25%+15%+5%=75%,
∴该县区八年级学生参加社会实践活动不少于3天的学生约为:5000×75%=3750名.
3750
巩固练习
(2)请对A,B两个县区八年级学生参加社会实践活动的天数情况进行比较,做出判断,并说明理由.
解:(2)∵A县区和B县区的平均活动天数均为3.85天,∴A县区和B县区的平均活动天数相同;∵A县区的中位数是3,B县区的中位数是2.5,∴B县区参加社会实践活动小于3天的人数比A县区多,从中位数看,A县区要好;∵A县区的众数是3,B县区的众数是4,∴A县区参加社会实践人数最多的是3天,B县区参加社会实践人数最多的是4天,从众数看,B县区要好.
考点三 极差、方差的计算及应用
考点分析
例(2023·山东)为备战东营市第十二届运动会,某县区对甲、乙、丙、丁四名射击运动员进行射击测试,他们射击测试成绩的平均数(单位:环)及方差S2(单位:环2)如下表所示:
甲 乙 丙 丁
9.6 8.9 9.6 9.6
S2 1.4 0.8 2.3 0.8
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择_______.
丁
解:选择一名成绩好的运动员,从平均数最大的运动员中选取,由表可知,甲,丙,丁的平均值最大,都是9.6,
∴从甲,丙,丁中选取,
∵甲的方差是1.4,丙的方差是2.3,丁的方差是0.8,
∴<<
∴发挥最稳定的运动员是丁,
∴从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择丁.
巩固练习
1.(2022秋·山东)若一组数据-1、0、2、4、x的极差为6,则x的值是( )
A.-2 B.2或-5 C.5 D.5或-2
D
2.(2023·四川眉山)已知一组数据为2,3,4,5,6,则该组数据的方差为( )
A.2 B.4 C.6 D.10
A
巩固练习
3.(2023·广西)甲、乙、丙、丁四名同学参加立定跳远训练,他们成绩的平均数相同,方差如下:=2.1,=3.5,=9,=0.7,则成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
D
4.(2023·四川)若一组数据的方差为2,则数据的方差是( )
A.2 B.5 C.6 D.11
A
当数据都加上一个数(或减去一个数)时,平均数也加或减这个数,方差不变,即数据的波动情况不变;
当数据都乘以一个数(或除以一个数)时,平均数也乘以或除以这个数,方差变为这个数的平方倍.
巩固练习
5.(2023·四川)小楠和小凯积极参加学校组织的科普大赛,下图是根据5次预赛成绩绘制的折线统计图,以下说法不合理的是( )
A.与小凯相比,小楠5次成绩的方差大
B.与小凯相比,小楠5次成绩的极差小
C.与小凯相比,小楠的成绩比较稳定
D.小凯的极差为11分
A
巩固练习
6.(2022·江苏扬州)某射击运动队进行了五次射击测试,甲、乙两名选手的测试成绩如图所示,甲、乙两选手成绩的方差分别记为、则.(填“>”“<”或“=”)
>
考点四 平均数、中位数、众数和方差的综合应用
考点分析
例(2023·广东)小红家到学校有两条公共汽车线路,为了解两条线路的乘车所用时间,小红做了试验,第一周(5个工作日)选择A线路,第二周(5个工作日)选择B线路,每天在固定时间段内乘车2次并分别记录所用时间,数据统计如下:(单位:min)
数据统计表
试验序号 1 2 3 4 5 6 7 8 9 10
A线路所用时间 15 32 15 16 34 18 21 14 35 20
B线路所用时间 25 29 23 25 27 26 31 28 30 24
数据折线统计图
考点分析
根据以上信息解答下列问题:
平均数 中位数 众数 方差
A线路所用时间 22 a 15 63.2
B线路所用时间 b 26.5 c 6.36
(1)填空:a=_____;b=______;c=_____;
(2)应用你所学的统计知识,帮助小红分析如何选择乘车线路.
19
26.8
25
解:(2)根据统计量上来分析可知,A线路所用时间平均数小于B线路所用时间平均数线路,A线路所用时间中位数也小于B线路所用时间中位数,但A线路所用时间的方差比较大,说明A线路比较短,但容易出现拥堵情况,B线路比较长,但交通畅通,总体上来讲A路线优于B路线.
考点分析
因此,我的建议是:根据上学到校剩余时间而定,如果上学到校剩余时间比较短,比如剩余时间是21分钟,则选择A路线,因为A路线的时间不大于21分钟的次数有7次,而B路线的时间都大于21分钟;如果剩余时间不短也不长,比如剩余时间是31分钟,则选择B路线,因为B路线的时间都不大于31分钟,而A路线的时间大于31分钟有3次,选择B路线可以确保不迟到;如果剩余时间足够长,比如剩余时间是36分钟,则选择A路线,在保证不迟到的情况,选择平均时间更少,中位数更小的路线.
巩固练习
1.(2022秋·江苏盐城)某个小作坊有5名员工(含老板),某一个月的工资(单位:元)为:3000,3000,3000,3000,10000,能反应这5名员工工资的集中趋势的是( )
A.平均数 B.中位数 C.方差 D.极差
B
平均数、中位数反应数据的集中趋势,方差反应数据的波动程度,极差反应数据的分散程度.
巩固练习
2.(2023·辽宁)某中学甲、乙两支国旗护卫队的队员身高(单位:cm)数据如下:
甲队:178,177,179,179,178,178,177,178,177,179;
乙队:178,177,177,176,178,175,177,181,180,181.
若要判断哪支护卫队队员身高更为整齐,应该比较两组数据的( )
A.平均数 B.众数 C.中位数 D.方差
D
巩固练习
3.(2023·山东)长时间观看手机、电脑等电子产品对视力影响非常大.6月6日是“全国爱眼日”,为了解学生的视力情况,某学校从甲、乙两个班级各随机抽取8名学生进行调查,并将统计数据绘制成如图所示的折线统计图,则下列说法正确的是( )
A.甲班视力值的平均数大于乙班视力值的平均数
B.甲班视力值的中位数大于乙班视力值的中位数
C.甲班视力值的极差小于乙班视力值的极差
D.甲班视力值的方差小于乙班视力值的方差
D
巩固练习
4.(2020·江苏连云港)“红色小讲解员”演讲比赛中,7位评委分别给出某位选手的原始评分.评定该选手成绩时,从7个原始评分中去掉一个最高分、一个最低分,得到5个有效评分.5个有效评分与7个原始评分相比,这两组数据一定不变的是( ).
A.中位数 B.众数 C.平均数 D.方差
A
巩固练习
5.(2023·河南)蓬勃发展的快递业,为全国各地的新鲜水果及时走进千家万户提供了极大便利.不同的快递公司在配送、服务、收费和投递范围等方面各具优势.樱桃种植户小丽经过初步了解,打算从甲、乙两家快递公司中选择一家合作,为此,小丽收集了10家樱桃种植户对两家公司的相关评价,并整理、描述、分析如下:
a.配送速度得分(满分10分):
甲:6 6 7 7 7 8 9 9 9 10
乙:6 7 7 8 8 8 8 9 9 10
b.服务质量得分统计图(满分10分):
巩固练习
c.配送速度和服务质量得分统计表:
项目统计量快递公司 配送速度得分 服务质量得分 平均数 中位数 平均数 方差
甲 7.8 m 7
乙 8 8 7
根据以上信息,回答下列问题:
(1)表格中的m=______;(填“>”“=”或“<”).
(2)综合上表中的统计量,你认为小丽应选择哪家公司?请说明理由.
7.5
<
解:(2)∵配送速度得分甲和乙的得分相差不大,
服务质量得分甲和乙的平均数相同,但是甲的方差明显小于乙的方差,
∴甲更稳定,
∴小丽应选择甲公司.
巩固练习
(3)为了从甲、乙两家公司中选出更合适的公司,你认为还应收集什么信息(列出一条即可)?
解:(3)还应收集甲、乙两家公司的收费情况.(答案不唯一,言之有理即可)
巩固练习
6.(2023春·河南)为了让师生更规范地操作教室里的一体机设备,学校信息中心制作了“教室一体机设备培训”视频,并在视频课时间进行播放.结束后为了解初一、初二各班一体机管理员对设备操作知识的掌握程度,信息中心对他们进行了相关的知识测试现从初一、初二年级各随机抽取了15名一体机管理员的成绩,得分用x表示,共分成4组:A:60≤x<70,B:70≤x<80,C:80≤x<90,D:90≤x<100,对得分进行整理分析,给出了下面部分信息:
初一年级一体机管理员的测试成绩在C组中的数据为:85,81,88.
初二年级一体机管理员的测试成绩:71,76,81,82,83,86,86,88,89,90,93,95,100,100,100.
巩固练习
成绩统计表如表:
(注:极差为样本中最大数据与最小数据差)
年级 平均数 中位数 最高分 众数 极差
初一 88 a 98 98 32
初二 88 88 100 b c
(1)a=_____,b=_______,c=_______;
(2)通过以上数据分析,你认为哪个年级的一体机管理员对一体机设备操作的知识掌握更好?并说明理由(写出一条理由即可).
85
100
29
解:(2)根据以上数据,我认为初二年级一体机管理员对设备操作的知识掌握更好.
理由:初一、初二两个年级的平均成绩一样,而初二年级的中位数、最高分、众数均高于初一年级,说明初二年级掌握更好
课堂小结
谈谈你本节课的收获是什么?
第3章 · 数据的集中趋势和离散程度
小结与思考
学习目标
1. 整理本章所学知识,构建本章知识框架 ;
2. 进一步理解平均数、众数和中位数的概念,会求一组数据的方差,并在理解概念的基础上,对生活中的某些数据进行分析,做出合理的判断与预测.
s2=[(x1-)2+(x2-)2+…+(xn-)2]
知识框架
数据的集中趋势和离散程度
数据的集中趋势
算术平均数
平均数
加权平均数
中位数
数据的离散程度
极 差
一组数据中出现次数最多的数据叫做这组数据的众数.
定义:一组数据中最大值与最小值的差叫做极差.
方 差
计算公式:极差=最大值-最小值
意义:反映一组数据的变化范围,在一定程度上描述了一组数据的离散(波动)程度.
圆内接四边形的对角互补.
一般地,将一组数据按大小顺序排列,
如果数据的个数是奇数,那么处于中间位置的数叫做这组数据的中位数;
如果数据的个数是偶数,那么处于中间位置的两个数的平均数叫做这组数据的中位数.
众 数
定义:用一组数据 x1 ,x2 ,…,xn 与它们的平均数的差的平方的平均数.
计算公式:
意义:反映一组数据的离散程度,方差越大(小),数据的波动越大(小)
=
=
(k≤n,f1+f2+f3+…+fk=n)
用样本平均数估计总体平均数
用样本方差估计总体方差
用样本估计总体
考点分析
考点一 平均数的计算及应用
例(2022·江苏盐城)合理的膳食可以保证青少年体格和智力的正常发育.综合实践小组为了解某校学生膳食营养状况,从该校1380名学生中调查了100名学生的膳食情况,调查数据整理如下:
中国营养学会推荐的三大营养素供能比参考值 蛋白质 10%~15%
脂肪 20%~30%
碳水化合物 50%~65%
注:供能比为某物质提供的能量占人体所需总能量的百分比.
考点分析
(1)本次调查采用___________的调查方法;(填“普查”或“抽样调查”)
(2)通过对调查数据的计算,样本中的蛋白质平均供能比约为14.6%,请计算样本中的脂肪平均供能比和碳水化合物平均供能比;
抽样调查
解:样本中所有学生的脂肪平均供能比为:
样本中所有学生的碳水化合物平均供能比为:
答:样本中的脂肪平均供能比为38.59%,碳水化合物平均供能比为46.825%.
考点分析
(3)结合以上的调查和计算,对照下表中的参考值,请你针对该校学生膳食状况存在的问题提一条建议.
解:(3)该校学生蛋白质平均供能比在合理的范围内,脂肪平均供能比高于参考值,碳水化合物供能比低于参考值,膳食不合理,营养搭配不均衡,建议增加碳水化合物的摄入量,减少脂肪的摄入量.(答案不唯一,建议合理即可)
巩固练习
1. (2020·江苏淮安) 已知一组数据1、3,a、10的平均数为5,则a=____.
6
2. (2023·湖南)某校组织青年教师教学竞赛活动,包含教学设计和现场教学展示两个方面.其中教学设计占20%,现场展示占80%.某参赛教师的教学设计90分,现场展示95分,则她的最后得分为______.
解:依题意,她的最后得分为:
90×20%+95×80%=94分
94
巩固练习
3.(2022·江苏泰州)学校要从王静,李玉两同学中选拔一人参加运动会志愿者工作,选拔项目为普通话,体育知识和旅游知识.并将成绩依次按4∶3∶3计分. 两人的各项选拔成绩如下表所示,则最终胜出的同学是_______.
∵81分>80分,
∴最终胜出的同学是李玉.
解:王静得分:
李玉得分:
普通话 体育知识 旅游知识
王静 80 90 70
李玉 90 80 70
李玉
4. (2022·江苏徐州) 如图,下列装在相同的透明密封盒内的古钱币,其密封盒上分别标有古钱币的尺寸及质量,例如:钱币“文星高照”密封盒上所标“45.4*2.8mm,24.4g”是指该枚古钱币的直径为45.4mm,厚度为2.8mm,质量为24.4g.已知这些古钱币的材质相同.
巩固练习
由于古钱币无法从密封盒内取出,为判断密封盒上所标古钱币的质量是否有错,桐桐用电子秤测得每枚古钱币与其密封盒的总质量如下:
名称 文星高照 状元及第 鹿鹤同春 顺风大吉 连中三元
总质量/g 58.7 58.1 55.2 54.3 55.8
请你应用所学的统计知识,判断哪枚古钱币所标的质量与实际质量差异较大,并计算该枚古钱币的实际质量约为多少克.
名称 文星高照 状元及第 鹿鹤同春 顺风大吉 连中三元
总质量/g 58.7 58.1 55.2 54.3 55.8
盒标质量 24.4 24.0 13.0 20.0 21.7
盒子质量 34.3 34.1 42.2 34.3 34.1
解:
∴“鹿鹤同春”密封盒的质量异常,故“鹿鹤同春”所标质量与实际质量差异较大.
其余四个盒子质量的平均数为:
g
55.2-34.2=21.0g,故“鹿鹤同春”的实际质量约为21.0克.
巩固练习
考点二 中位数和众数的计算及应用
考点分析
例(2021·江苏南京)某市在实施居民用水定额管理前,对居民生活用水情况进行了调查,通过简单随机抽样,获得了100个家庭去年的月均用水量数据,将这组数据按从小到大的顺序排列,其中部分数据如下表:
序号 1 2 … 25 26 … 50 51 … 75 76 … 99 100
月均用水量/t 1.3 1.3 … 4.5 4.5 … 6.4 6.8 … 11 13 … 25.6 28
(1)求这组数据的中位数.已知这组数据的平均数为9.2t,你对它与中位数的差异有什么看法?
解:(1)由表格数据可知,位于最中间的两个数分别是6.4和6.8,
t
∴中位数为:
考点分析
而这组数据的平均数为9.2t,它们之间差异较大,主要是因为它们各自的特点决定的,主要原因如下:①因为平均数与每一个数据都有关,其中任何数据的变动都会相应引起平均数的变动;主要缺点是易受极端值的影响,这里的极端值是指偏大或偏小数,当出现偏大数时,平均数将会被抬高,当出现偏小数时,平均数会降低;②中位数将数据按照从小到大或从大到小的顺序排列,如果数据个数是奇数,则处于最中间位置的数就是这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数是这组数据的中位数,它的求出不需或只需简单的计算,它不受极端值的影响.这100个数据中,最大的数据是28,最小的是1.3,因此平均数受到极端值的影响,造成与中位数差异较大.
考点分析
(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使75%的家庭水费支出不受影响,你觉得这个标准应该定为多少?
(2)因为第75户用数量为11t,第76户用数量为13t,因此标准应定为11≤a<13(其中 a为标准用水量,单位:t).
为了鼓励节约用水则标准应定为11t.
巩固练习
1. (2023·江苏徐州) 徐州云龙山共九节,蜿蜒起伏,形似游龙,每节山的海拔如图所示.
其中,海拔为中位数的是( )
A.第五节山 B.第六节山 C.第八节山 D.第九节山
C
2. (2023·江苏泰州) 七(1)班40名同学上周家务劳动时间的频数分布直方图如图所示,设这组数据的中位数为mh,则m_____2.6(填“>”“=“<”)
解:因为有40个数据,中位数应是数据有小到大排
列第20、21个数据的平均数,由频数分布直方图可知:第1-5组的人数分别为5,7,12,9,7,
所以第20、21个数据都在第3组,即2.0-2.5,这两个数的平均数一定小于2.6.
<
巩固练习
30
巩固练习
3.(2022·江苏淮安)某公司对25名营销人员4月份销售某种商品的情况统计如下:
销售量(件) 60 50 40 35 30 20
人数 1 4 4 6 7 3
则这25名营销人员销售量的众数是_________.
巩固练习
4. (2022·江苏南通)为了了解八年级学生本学期参加社会实践活动的天数情况,A、B两个县区分别随机抽查了200名八年级学生.根据调查结果绘制了统计图表,部分图表如下:
A、B两个县区的统计表
平均数 众数 中位数
A县区 3.85 3 3
B县区 3.85 4 2.5
(1)若A县区八年级共有约5000名学生,估计该县区八年级学生参加社会实践活动不少于3天的学生约为______名;
(1) 解:根据A县区统计图得,该县区八年级学生参加社会实践活动不少于3天的比例为:30%+25%+15%+5%=75%,
∴该县区八年级学生参加社会实践活动不少于3天的学生约为:5000×75%=3750名.
3750
巩固练习
(2)请对A,B两个县区八年级学生参加社会实践活动的天数情况进行比较,做出判断,并说明理由.
解:(2)∵A县区和B县区的平均活动天数均为3.85天,∴A县区和B县区的平均活动天数相同;∵A县区的中位数是3,B县区的中位数是2.5,∴B县区参加社会实践活动小于3天的人数比A县区多,从中位数看,A县区要好;∵A县区的众数是3,B县区的众数是4,∴A县区参加社会实践人数最多的是3天,B县区参加社会实践人数最多的是4天,从众数看,B县区要好.
考点三 极差、方差的计算及应用
考点分析
例(2023·山东)为备战东营市第十二届运动会,某县区对甲、乙、丙、丁四名射击运动员进行射击测试,他们射击测试成绩的平均数(单位:环)及方差S2(单位:环2)如下表所示:
甲 乙 丙 丁
9.6 8.9 9.6 9.6
S2 1.4 0.8 2.3 0.8
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择_______.
丁
解:选择一名成绩好的运动员,从平均数最大的运动员中选取,由表可知,甲,丙,丁的平均值最大,都是9.6,
∴从甲,丙,丁中选取,
∵甲的方差是1.4,丙的方差是2.3,丁的方差是0.8,
∴<<
∴发挥最稳定的运动员是丁,
∴从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择丁.
巩固练习
1.(2022秋·山东)若一组数据-1、0、2、4、x的极差为6,则x的值是( )
A.-2 B.2或-5 C.5 D.5或-2
D
2.(2023·四川眉山)已知一组数据为2,3,4,5,6,则该组数据的方差为( )
A.2 B.4 C.6 D.10
A
巩固练习
3.(2023·广西)甲、乙、丙、丁四名同学参加立定跳远训练,他们成绩的平均数相同,方差如下:=2.1,=3.5,=9,=0.7,则成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
D
4.(2023·四川)若一组数据的方差为2,则数据的方差是( )
A.2 B.5 C.6 D.11
A
当数据都加上一个数(或减去一个数)时,平均数也加或减这个数,方差不变,即数据的波动情况不变;
当数据都乘以一个数(或除以一个数)时,平均数也乘以或除以这个数,方差变为这个数的平方倍.
巩固练习
5.(2023·四川)小楠和小凯积极参加学校组织的科普大赛,下图是根据5次预赛成绩绘制的折线统计图,以下说法不合理的是( )
A.与小凯相比,小楠5次成绩的方差大
B.与小凯相比,小楠5次成绩的极差小
C.与小凯相比,小楠的成绩比较稳定
D.小凯的极差为11分
A
巩固练习
6.(2022·江苏扬州)某射击运动队进行了五次射击测试,甲、乙两名选手的测试成绩如图所示,甲、乙两选手成绩的方差分别记为、则.(填“>”“<”或“=”)
>
考点四 平均数、中位数、众数和方差的综合应用
考点分析
例(2023·广东)小红家到学校有两条公共汽车线路,为了解两条线路的乘车所用时间,小红做了试验,第一周(5个工作日)选择A线路,第二周(5个工作日)选择B线路,每天在固定时间段内乘车2次并分别记录所用时间,数据统计如下:(单位:min)
数据统计表
试验序号 1 2 3 4 5 6 7 8 9 10
A线路所用时间 15 32 15 16 34 18 21 14 35 20
B线路所用时间 25 29 23 25 27 26 31 28 30 24
数据折线统计图
考点分析
根据以上信息解答下列问题:
平均数 中位数 众数 方差
A线路所用时间 22 a 15 63.2
B线路所用时间 b 26.5 c 6.36
(1)填空:a=_____;b=______;c=_____;
(2)应用你所学的统计知识,帮助小红分析如何选择乘车线路.
19
26.8
25
解:(2)根据统计量上来分析可知,A线路所用时间平均数小于B线路所用时间平均数线路,A线路所用时间中位数也小于B线路所用时间中位数,但A线路所用时间的方差比较大,说明A线路比较短,但容易出现拥堵情况,B线路比较长,但交通畅通,总体上来讲A路线优于B路线.
考点分析
因此,我的建议是:根据上学到校剩余时间而定,如果上学到校剩余时间比较短,比如剩余时间是21分钟,则选择A路线,因为A路线的时间不大于21分钟的次数有7次,而B路线的时间都大于21分钟;如果剩余时间不短也不长,比如剩余时间是31分钟,则选择B路线,因为B路线的时间都不大于31分钟,而A路线的时间大于31分钟有3次,选择B路线可以确保不迟到;如果剩余时间足够长,比如剩余时间是36分钟,则选择A路线,在保证不迟到的情况,选择平均时间更少,中位数更小的路线.
巩固练习
1.(2022秋·江苏盐城)某个小作坊有5名员工(含老板),某一个月的工资(单位:元)为:3000,3000,3000,3000,10000,能反应这5名员工工资的集中趋势的是( )
A.平均数 B.中位数 C.方差 D.极差
B
平均数、中位数反应数据的集中趋势,方差反应数据的波动程度,极差反应数据的分散程度.
巩固练习
2.(2023·辽宁)某中学甲、乙两支国旗护卫队的队员身高(单位:cm)数据如下:
甲队:178,177,179,179,178,178,177,178,177,179;
乙队:178,177,177,176,178,175,177,181,180,181.
若要判断哪支护卫队队员身高更为整齐,应该比较两组数据的( )
A.平均数 B.众数 C.中位数 D.方差
D
巩固练习
3.(2023·山东)长时间观看手机、电脑等电子产品对视力影响非常大.6月6日是“全国爱眼日”,为了解学生的视力情况,某学校从甲、乙两个班级各随机抽取8名学生进行调查,并将统计数据绘制成如图所示的折线统计图,则下列说法正确的是( )
A.甲班视力值的平均数大于乙班视力值的平均数
B.甲班视力值的中位数大于乙班视力值的中位数
C.甲班视力值的极差小于乙班视力值的极差
D.甲班视力值的方差小于乙班视力值的方差
D
巩固练习
4.(2020·江苏连云港)“红色小讲解员”演讲比赛中,7位评委分别给出某位选手的原始评分.评定该选手成绩时,从7个原始评分中去掉一个最高分、一个最低分,得到5个有效评分.5个有效评分与7个原始评分相比,这两组数据一定不变的是( ).
A.中位数 B.众数 C.平均数 D.方差
A
巩固练习
5.(2023·河南)蓬勃发展的快递业,为全国各地的新鲜水果及时走进千家万户提供了极大便利.不同的快递公司在配送、服务、收费和投递范围等方面各具优势.樱桃种植户小丽经过初步了解,打算从甲、乙两家快递公司中选择一家合作,为此,小丽收集了10家樱桃种植户对两家公司的相关评价,并整理、描述、分析如下:
a.配送速度得分(满分10分):
甲:6 6 7 7 7 8 9 9 9 10
乙:6 7 7 8 8 8 8 9 9 10
b.服务质量得分统计图(满分10分):
巩固练习
c.配送速度和服务质量得分统计表:
项目统计量快递公司 配送速度得分 服务质量得分 平均数 中位数 平均数 方差
甲 7.8 m 7
乙 8 8 7
根据以上信息,回答下列问题:
(1)表格中的m=______;(填“>”“=”或“<”).
(2)综合上表中的统计量,你认为小丽应选择哪家公司?请说明理由.
7.5
<
解:(2)∵配送速度得分甲和乙的得分相差不大,
服务质量得分甲和乙的平均数相同,但是甲的方差明显小于乙的方差,
∴甲更稳定,
∴小丽应选择甲公司.
巩固练习
(3)为了从甲、乙两家公司中选出更合适的公司,你认为还应收集什么信息(列出一条即可)?
解:(3)还应收集甲、乙两家公司的收费情况.(答案不唯一,言之有理即可)
巩固练习
6.(2023春·河南)为了让师生更规范地操作教室里的一体机设备,学校信息中心制作了“教室一体机设备培训”视频,并在视频课时间进行播放.结束后为了解初一、初二各班一体机管理员对设备操作知识的掌握程度,信息中心对他们进行了相关的知识测试现从初一、初二年级各随机抽取了15名一体机管理员的成绩,得分用x表示,共分成4组:A:60≤x<70,B:70≤x<80,C:80≤x<90,D:90≤x<100,对得分进行整理分析,给出了下面部分信息:
初一年级一体机管理员的测试成绩在C组中的数据为:85,81,88.
初二年级一体机管理员的测试成绩:71,76,81,82,83,86,86,88,89,90,93,95,100,100,100.
巩固练习
成绩统计表如表:
(注:极差为样本中最大数据与最小数据差)
年级 平均数 中位数 最高分 众数 极差
初一 88 a 98 98 32
初二 88 88 100 b c
(1)a=_____,b=_______,c=_______;
(2)通过以上数据分析,你认为哪个年级的一体机管理员对一体机设备操作的知识掌握更好?并说明理由(写出一条理由即可).
85
100
29
解:(2)根据以上数据,我认为初二年级一体机管理员对设备操作的知识掌握更好.
理由:初一、初二两个年级的平均成绩一样,而初二年级的中位数、最高分、众数均高于初一年级,说明初二年级掌握更好
课堂小结
谈谈你本节课的收获是什么?
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
