数学人教A版(2019)选择性必修第一册2.5.2圆与圆的位置关系课件(共50张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.5.2圆与圆的位置关系课件(共50张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 07:27:07 | ||
图片预览









文档简介
(共50张PPT)
第二章《直线和圆的方程》2.5.2 圆与圆的位置关系了解圆与圆的位置关系.
掌握圆与圆的位置关系的判断方法
能用圆与圆的位置关系解决一些简单问题
学习目标
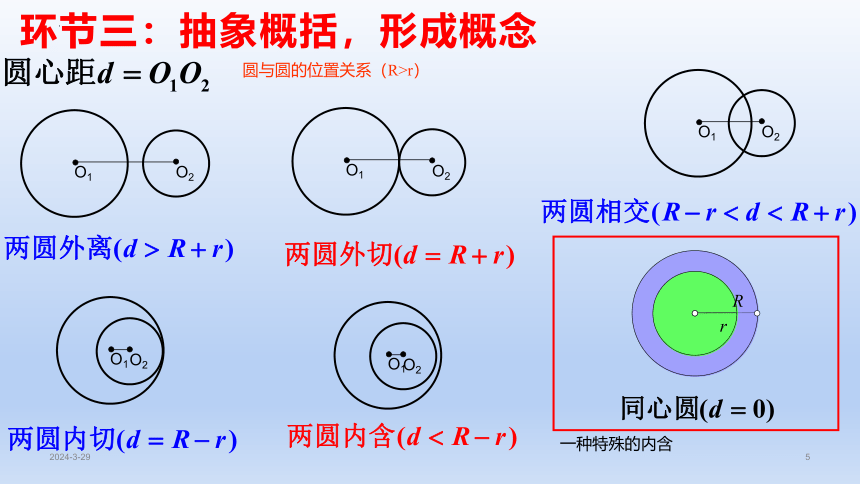
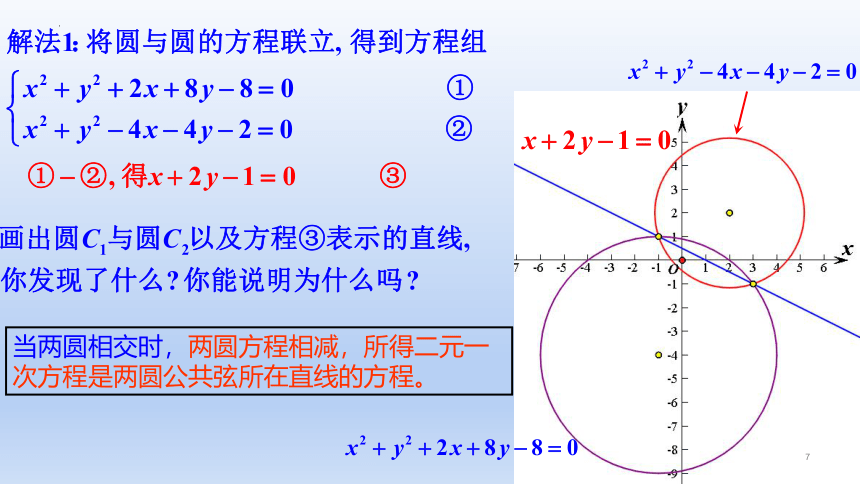
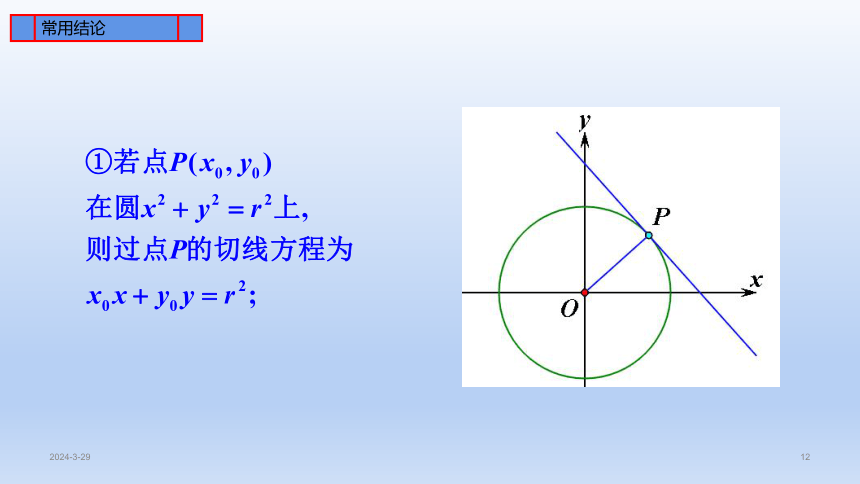
【实际情境】每逢节假日农村集市上出现各式各样套圈活动,套硬币更是博人眼球,商家圈起来一小片空地,撒满一元,五角和一角的硬币,玩家花10元钱可套30环,看似简单套起来却没有那么容易,要求套环落地后不触碰硬币,毕竟硬币面值越大,想套中就越难。问题1:(1)每次套圈时把目标硬币和套环看成两个圆,那么这两个圆满足什么位置关系才算套中?(2)为什么硬币面值越大,想套中就越难?(3)两个圆的位置关系和圆心距以及半径存在怎样的数量关系?环节一:创设情境,引入课题前面我们运用直线的方程、圆的方程,研究了直线与圆的位置关系.现在我们类比上述研究方法,运用圆的方程,通过定量计算研究圆与圆的位置关系.我们知道,两个圆之间存在以下三种位置关系:(1)两圆相交,有两个公共点;(2)两圆相切,包括外切与内切,只有一个公共点;(3)两圆相离,包括外离与内含,没有公共点.思考类比运用直线和圆的方程,研究直线与圆的位置关系的方法,如何利用圆的方程,判断它们之间的位置关系?环节二:观察分析,感知概念O1O2O1O2O1O2O1O2O1O2圆与圆的位置关系(R>r)rR一种特殊的内含环节三:抽象概括,形成概念环节四:辨析理解,深化概念当两圆相交时,两圆方程相减,所得二元一次方程是两圆公共弦所在直线的方程。yxABC2C1图2.5-6yxABC2C1图2.5-6AOBPMxy图2.5-7分析:我们可以通过建立适当的平面直角坐标系,求得满足条件的动点M的轨迹方程,从而得到点M的轨迹;通过研究它的轨迹方程与圆O方程的关系,判断这个轨迹与圆O的位置关系.环节五:课堂练习,巩固运用常用结论常用结论常用结论环节六:归纳总结,反思提升1.知识清单:(1)两圆的位置关系.(2)两圆的公共弦.(3)圆系方程.(4)圆与圆的综合性问题.2.方法归纳:几何法、代数法.3.常见误区:将两圆内切和外切相混.环节七:目标检测,作业布置教科书习题2.5第7,8,10题.练习(第98页)习题2.5(第98页)OMECxyABMCC1解法二:相交圆系BACOxyBACOxy解法二:相交圆系CABMOxyMNCFEMNCFE11.如图,某台机器的三个轮齿,A和B啮合,C和B也啮合.若A轮的直径为200 cm,B轮的直径为120 cm,C轮的直径为250 cm,且∠A=45°.试建立适当的坐标系,用坐标法求出A,C两齿轮的中心距离(精确到1 cm).
第二章《直线和圆的方程》2.5.2 圆与圆的位置关系了解圆与圆的位置关系.
掌握圆与圆的位置关系的判断方法
能用圆与圆的位置关系解决一些简单问题
学习目标
【实际情境】每逢节假日农村集市上出现各式各样套圈活动,套硬币更是博人眼球,商家圈起来一小片空地,撒满一元,五角和一角的硬币,玩家花10元钱可套30环,看似简单套起来却没有那么容易,要求套环落地后不触碰硬币,毕竟硬币面值越大,想套中就越难。问题1:(1)每次套圈时把目标硬币和套环看成两个圆,那么这两个圆满足什么位置关系才算套中?(2)为什么硬币面值越大,想套中就越难?(3)两个圆的位置关系和圆心距以及半径存在怎样的数量关系?环节一:创设情境,引入课题前面我们运用直线的方程、圆的方程,研究了直线与圆的位置关系.现在我们类比上述研究方法,运用圆的方程,通过定量计算研究圆与圆的位置关系.我们知道,两个圆之间存在以下三种位置关系:(1)两圆相交,有两个公共点;(2)两圆相切,包括外切与内切,只有一个公共点;(3)两圆相离,包括外离与内含,没有公共点.思考类比运用直线和圆的方程,研究直线与圆的位置关系的方法,如何利用圆的方程,判断它们之间的位置关系?环节二:观察分析,感知概念O1O2O1O2O1O2O1O2O1O2圆与圆的位置关系(R>r)rR一种特殊的内含环节三:抽象概括,形成概念环节四:辨析理解,深化概念当两圆相交时,两圆方程相减,所得二元一次方程是两圆公共弦所在直线的方程。yxABC2C1图2.5-6yxABC2C1图2.5-6AOBPMxy图2.5-7分析:我们可以通过建立适当的平面直角坐标系,求得满足条件的动点M的轨迹方程,从而得到点M的轨迹;通过研究它的轨迹方程与圆O方程的关系,判断这个轨迹与圆O的位置关系.环节五:课堂练习,巩固运用常用结论常用结论常用结论环节六:归纳总结,反思提升1.知识清单:(1)两圆的位置关系.(2)两圆的公共弦.(3)圆系方程.(4)圆与圆的综合性问题.2.方法归纳:几何法、代数法.3.常见误区:将两圆内切和外切相混.环节七:目标检测,作业布置教科书习题2.5第7,8,10题.练习(第98页)习题2.5(第98页)OMECxyABMCC1解法二:相交圆系BACOxyBACOxy解法二:相交圆系CABMOxyMNCFEMNCFE11.如图,某台机器的三个轮齿,A和B啮合,C和B也啮合.若A轮的直径为200 cm,B轮的直径为120 cm,C轮的直径为250 cm,且∠A=45°.试建立适当的坐标系,用坐标法求出A,C两齿轮的中心距离(精确到1 cm).
