人教版四年级数学上册第三单元角的度量(知识点梳理+能力百分练)一(含解析)
文档属性
| 名称 | 人教版四年级数学上册第三单元角的度量(知识点梳理+能力百分练)一(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 829.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 08:15:54 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版四年级上册第三单元角的度量(知识点梳理+能力百分练)一
知识点梳理
1、线段、射线与直线的区别与联系:线段有两个端点,长度有限,不能延伸,可以测量;直线没有端点,无限长,向两端无限延伸,不可以测量;射线有一个端点,无限长,向一端无限延伸,不可以测量。直线和射线没有具体的长度.
2、线段、射线和直线的特点:经过一-点可以两无数条射线和直线,经过两点只能画一条直线。
3、角是从一点引出两条射线所组成的图形.所以它的两条边可以无限延伸,并不是边越长,角的度数越大。
4、角通常用符号“∠”表示,例如角1可以记作∠1.
5、角的计量单位是“度”,用符号“。”表示,将圆分成360等份,其中的1份所对的角是1度,记作1°。
6、使用量角器要做到“两合一看”。即把量角器的中心与角的顶点重合,0"刻度线与角的一条边重合,角的另一条边所对的量角器上的刻度,就是这个角的度数。
7、用三角尺可以画一些特殊度数的角,如30° ,60° ,90°等。
8、角分为五类:0°<锐角<90°、直角= 90°、90°<钝角< 180°、平角= 180°、周角= 360°。它们的大小关系是:锐角<直角<钝角<平角<周角。
能力百分练
一、选择题(共16分)
1.下面图形中,( )是射线。
A. B.
C. D.
2.下面关系中,正确的是( )。
A.1周角=4平角=2直角 B.1周角=2平角=3直角
C.1周角=2平角=4直角 D.1周角=3平角=4直角
3.用一副三角板不能拼出的角是( )。
A.75° B.120° C.150° D.160°
4.下面的各角中,可以用一副三角板画出来的是( )。
A.100° B.125° C.85° D.105°
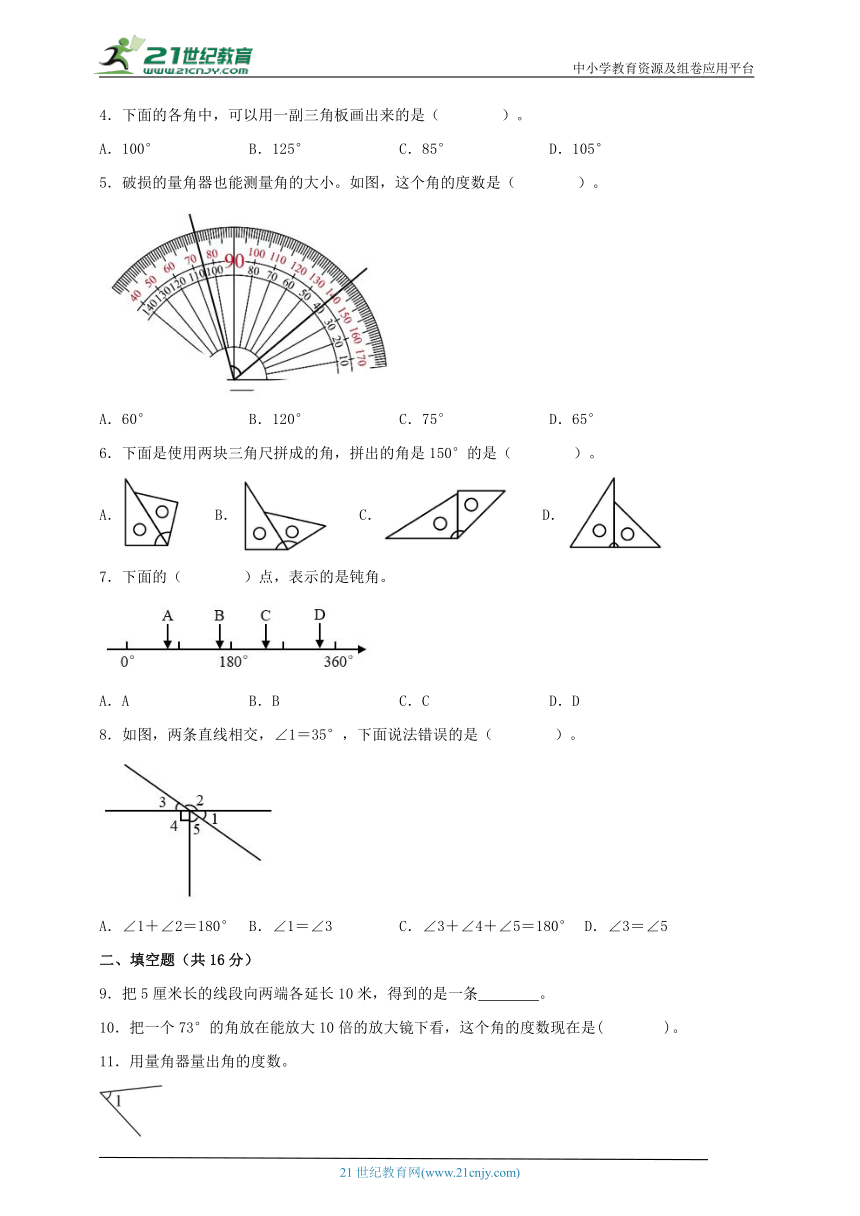
5.破损的量角器也能测量角的大小。如图,这个角的度数是( )。
A.60° B.120° C.75° D.65°
6.下面是使用两块三角尺拼成的角,拼出的角是150°的是( )。
A. B. C. D.
7.下面的( )点,表示的是钝角。
A.A B.B C.C D.D
8.如图,两条直线相交,∠1=35°,下面说法错误的是( )。
A.∠1+∠2=180° B.∠1=∠3 C.∠3+∠4+∠5=180° D.∠3=∠5
二、填空题(共16分)
9.把5厘米长的线段向两端各延长10米,得到的是一条 。
10.把一个73°的角放在能放大10倍的放大镜下看,这个角的度数现在是( )。
11.用量角器量出角的度数。
∠1=( )。
12.把长方形的一个角折叠,如图所示。∠1=32°,那么∠2的度数是 。
13.如图,直线AB上共有( )条线段,( )条射线。
14.将一张圆形纸片对折3次后展开,相邻两条折痕所形成的角是( )度。
15.用一副三角尺拼出的最大钝角是( )度。
16.把一个平角分成两个角,如果其中一个角是锐角,那么另一个角是( )角。
三、判断题(共8分)
17.大于180°而小于90°的角是钝角。( )
18.角的边越短,角就越小。( )
19.如图,图中共有8个角。( )
20.奇思画了一条长0.2米的直线。( )
四、计算题(共6分)
21.(6分)求出下面各角的度数。
已知图中∠1=52°,求出∠2、∠3。
五、连线题(共6分)
22.(6分)红花配绿叶,连一连。
六、作图题(共12分)
23.(6分)用量角器画一个65°的角(保留作图痕迹)。
24.(6分)过点A画一条射线,并在射线上截取一条2厘米长的线段。
七、解答题(共36分)
25.(6分)你能猜出这几个角的度数吗?并说明原因。
26.(6分)如图所示,∠1=∠2,你能说明∠3和∠4相等吗?
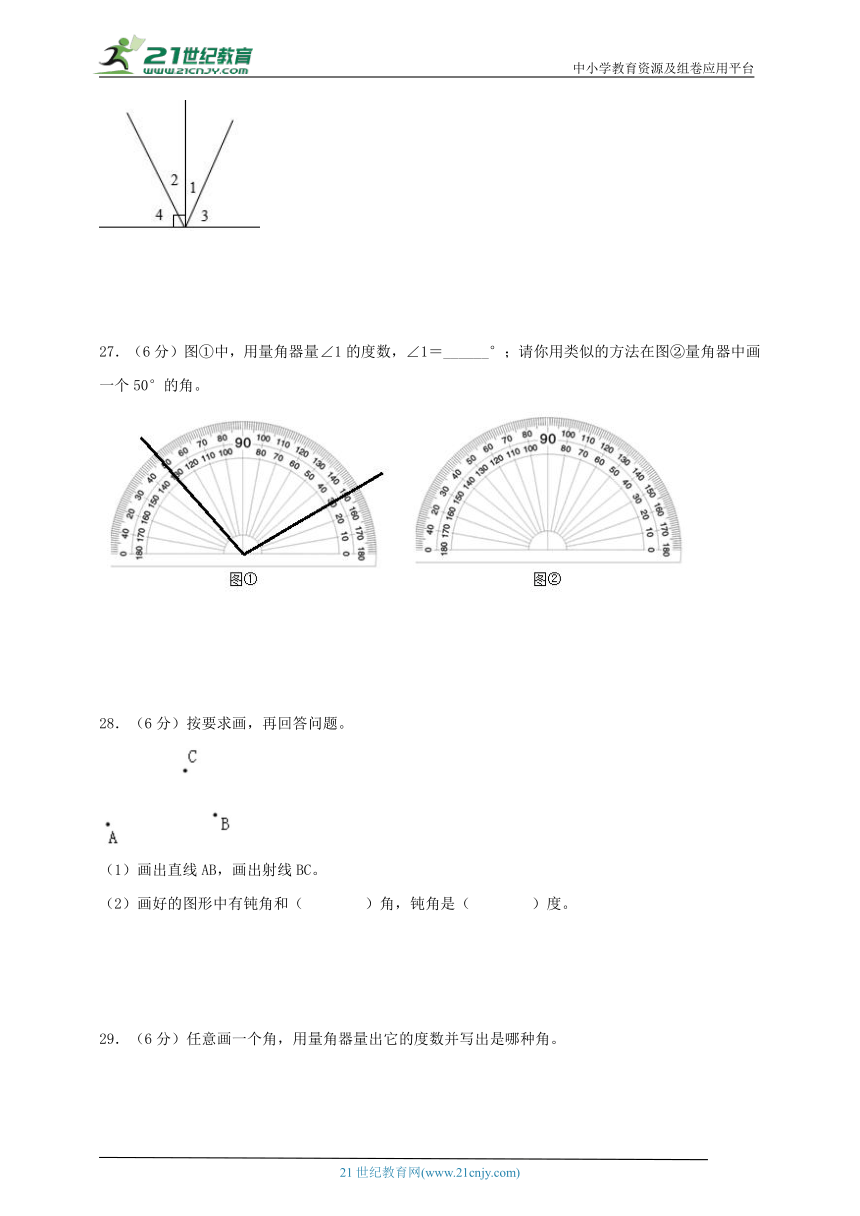
27.(6分)图①中,用量角器量∠1的度数,∠1=______°;请你用类似的方法在图②量角器中画一个50°的角。
28.(6分)按要求画,再回答问题。
(1)画出直线AB,画出射线BC。
(2)画好的图形中有钝角和( )角,钝角是( )度。
29.(6分)任意画一个角,用量角器量出它的度数并写出是哪种角。
30.(6分)把下列线进行分类,找出各类线之间有什么相同和不同之处?
参考答案
1.C
【分析】把线段向一端无限延伸,就得到一条射线,射线只有一个端点,据此解答即可。
【详解】A.有两个端点,是线段;
B.从一点引出两条射线所组成的图形叫做角;
C.只有一个端点,是射线;
D.没有端点,是直线。
故答案为:C
【点睛】此题主要考查线段、直线、射线以及角的认识与特征。
2.C
【分析】周角等于360度,平角等于180度,直角等于90度,据此计算解答。
【详解】360°÷180°=2(个)
180°÷90°=2(个)
360°÷90°=4(个)
所以1周角=2平角=4直角。
故答案为:C
【点睛】本题考查了周角、平角及直角之间的关系。
3.D
【分析】一副三角板,其中一个三角板的角有30°、60°、90°,等腰直角三角板的角有45°、45°、90°,用它们进行拼组,即可解答。
【详解】A.30°+45°=75°,用一副三角板能拼出75°的角;
B.90°+30°=120°,用一副三角板能拼出120°的角;
C.90°+60°=150°,用一副三角板能拼出150°的角;
D.用一副三角板不能拼出160°的角。
故答案为:D
【点睛】本题考查了学生用一副三角板拼成不同角度的能力。
4.D
【分析】一副三角板中的各个角的度数分别是30°、60°、45°、90°。将它们进行组合,可得到的角有60°-45°=15°,60°+45°=105°,60°+90°=150°,90°+45°=135°,90°+30°=120°,30°+45°=75°,据此即可解答。
【详解】A.不可以用一副三角板拼成100°;
B.不可以用一副三角板拼成125°;
C.不可以用一副三角板拼成 85°;
D.60°+45°=105°,所以能用一副三角板拼成105°;
故答案为:D
【点睛】本题考查了学生用一副三角尺拼成角度情况的掌握,能用一副三角尺画出的角都是15°的整数倍。
5.D
【分析】根据图示,量角器显示这个角在75°和140°之间,利用大度数减小度数即可得到角的度数。
【详解】140°-75°=65°
这个角的度数是65°。
故答案为:D
【点睛】本题主要考查学生利用量角器测量角的度数的能力。
6.B
【分析】一副三角尺中的各个角的度数分别是30°、60°、45°、90°,求拼出的角的度数,把两个角的度数相加即可。
【详解】A.60°+45°=105°
B.60°+90°=150°
C.90°+30°=120°
D.90°+90°=180°
所以拼出的角是150°的是。
故答案为:B
【点睛】本题主要考查图形的拼组,关键是利用三角尺各角的度数解答。
7.B
【分析】钝角指的是角度大于90°小于180°的角,据此即可解答。
【详解】从图中可以看出A小于90°,C、D大于180°,B处在90°到180°之间。
故答案为:B
【点睛】本题考查的是角度的分类,弄清钝角的概念是关键。
8.D
【分析】根据题图可知,∠1和∠2组成一个平角,则∠1+∠2=180°。∠2和∠3组成一个平角,则∠2+∠3=180°。也就是∠1=∠3。∠3、∠4和∠5组成一个平角,则∠3+∠4+∠5=180°。∠1和∠5组成一个直角,则∠5=90°-∠1,而∠1=∠3,则∠3≠∠5。
【详解】A.∠1+∠2=180°,说法正确;
B.∠1=∠3=180°-∠2,说法正确;
C.∠3+∠4+∠5=180°,说法正确;
D.∠3=∠1=35°,∠5=90°-∠1=90°-35°=55°,则∠3≠∠5。说法错误。
故答案为:D
【点睛】解决此类问题时,要善于利用图中隐藏的特殊角(直角、平角、周角),以及它与各角之间的关系,利用已知角,求出未知角。
9.线段
【分析】根据线段的含义:线段有两个端点,有限长;据此解答即可。
【详解】把5厘米长的线段向两端各延长10米,得到的是一条线段。
【点睛】此题考查了线段的含义,应注意理解和掌握。
10.73°/73度
【分析】用放大镜看角时,放大的是角的边,不改变角的形状和大小,据此解答。
【详解】把一个73°的角放在能放大10倍的放大镜下看,这个角的度数现在是73°。
【点睛】本题主要考查角的度量,解题关键是正确掌握放大镜的特性,只改变边的长度,而不能改变角的开口大小。
11.50°
【分析】用量角器度量角的方法是:把量角器的中心与角的顶点重合,0刻度线与边的一边重合,角的另一边所经过的量角器上所显示的刻度就是被量角的度数。
【详解】用量角器量出角的度数,∠1=50°。
【点睛】用量角器量角要做“两重合”,“一看准”。“两重合”是先把量角器的中心与角的顶点重重合;把量角器的零刻度线与角的一边重合;“一看准”是指最后看角的另一边所对的量角器上的刻度,就是所量的角的度数。
12.26°
【分析】长方形的4个角都是直角。将一个角折叠后,∠1盖住了一个与它度数相等的角,也就是2∠1与∠2的和是90°,∠2=90°-2×∠1,据此解答。
【详解】∠2=90°-32×2°
=90°-64°
=26°
【点睛】解决此类问题时,要善于利用图中隐藏的特殊角(直角、平角、周角),以及它与各角之间的关系,利用已知角,求出未知角。
13. 6 8
【分析】由题目可知,从短到长,线段共有(3+2+1)条,每个端点发出两条射线,所以共8条射线,即可解题。
【详解】由分析可知:
3+2+1=6(条)
所以直线AB上共有6条线段,8条射线。
【点睛】此题主要考查了线段和射线的定义,要熟练掌握。
14.45
【分析】一张圆形的纸片,圆心角是360度,对折一次,就是把圆心角平均分成2份,得到两个180度的平角,再对折一次就把平角再平均分成2个一样的90度直角,再对折又把直角平均分成了45度的角,据此解答。
【详解】如图所示:
360÷2÷2÷2
=180÷2÷2
=90÷2
=45(度)
将一张圆形纸片对折3次后展开,相邻两条折痕所形成的角是45度。
【点睛】本题考查了周角、平角及直角的认识。解答此题时,可亲自动手操作一下。
15.150
【分析】一副三角尺有两个直角三角板,其中一个直角三角板的角度数分别是30度,60度,90度,另一个直角三角板的角度数分别是45度,45度,90度,结合钝角是大于90度且小于180度的角,即可解答。
【详解】根据分析可知,用一副三角尺能够拼出的钝角有:
30+90=120(度)
60+45=105(度)
60+90=150(度)
所以用一副三角尺拼出的最大钝角是150度。
【点睛】本题主要考查用三角板拼角和角的分类,属于基础知识,要熟练掌握。
16.钝
【分析】根据锐角、直角、钝角、平角的意义,小于90度的角叫做锐角;等于90度的角叫做直角;大于90度小于180度的角叫做钝角,等于180度的角叫做平角,据此解答即可。
【详解】由分析可知:平角=锐角+钝角,所以把一个平角分成两个角,如果其中一个角是锐角,那么另一个角一定是钝角。
【点睛】此题考查的目的是理解掌握锐角、直角、钝角、平角的意义,需熟练掌握。
17.×
【详解】
如图所示,∠1是一个钝角。小于180°大于90°的角是钝角,题干说法错误。
故答案为:×
18.×
【分析】根据角的概念:由一点引出的两条射线所围成的图形,叫做角;角的大小与两条边的长短(射线,无限长)无关,只与开口的大小有关;进而判断即可。
【详解】由分析可知:角的大小只与开口的大小有关,与两条边的长短无关;所以原题的说法错误。
故答案为:×
【点睛】此题考查了角的概念和影响角的大小的因素。
19.×
【分析】图中5条射线,每相邻两条射线组成1个小角,这样的小角有4个,每相邻两个小角合成1个角,这样的角有3个,相邻三个小角合成一个角,这样的角有2个,全部4个小角合成1个角;据此解答即可。
【详解】1+2+3+4
=3+3+4
=6+4
=10(个)
所以,图中共有10个角,故原题说法错误。
故答案为:×
【点睛】此题重点考查在多个角组成的组合图形中计角个数的方法。
20.×
【分析】一根拉紧的线、紧绷的弦都可以看作线段,线段有两个端点,可以测量出长度;把线段向两端无限延伸就可以得到一条直线,直线没有端点,是无限长的,因此不可以测量出长度,依此判断。
【详解】奇思画了一条长0.2米的线段,原题干说法错误。
故答案为:×
【点睛】熟练掌握直线、线段的特点是解答此题的关键。
21.∠2=38°;∠3=142°
【分析】1直角=90°,1平角=180°,根据题意可知:∠1+∠2+90°=180°,因此∠2=180°-90°-∠1;∠3+∠2=180°,因此∠3=180°-∠2;依此计算。
【详解】∠2=180°-90°-52°=90°-52°=38°;
∠3=180°-38°=142°。
即∠2=38°,∠3=142°。
22.见详解
【分析】根据锐角、钝角、直角、平角、周角的含义可知:锐角是大于0°小于90°的角;钝角是大于90°小于180°的角;直角是等于90°的角;平角是等于180°的角;周角是等于360°的角;据此连线即可。
【详解】
【点睛】熟悉锐角、直角、钝角、平角、周角的度数范围是解答此题的关键。
23.见详解
【分析】画一条射线,使量角器的中心和射线的端点重合,0°刻度线和射线重合。在量角器65°刻度线的地方点一个点。以画出的射线的端点为端点,通过刚画的点,再画一条射线。据此画出65°的角。
【详解】
【点睛】本题考查用量角器画角的方法。画角注意两重和,量角器的中心和射线的端点重合,0°刻度线和射线重合。
24.见解答
【分析】射线只有一个端点,因此以点A为端点向一边画一条直的线即可得到一条射线;
线段有两个端点,因此可以以A点为线段的一个端点,并且使A点对准直尺的0刻度线,直尺紧靠所画的射线,2厘米处就是这条线段的另一个端点,依此画图即可。
【详解】画图如下:
【点睛】熟练掌握射线、线段的特点,是解答此题的关键。
25.30°;可能是110°或70°(原因见详解)
【分析】量角的步骤是:先把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合,角的另一边所对的量角器上的刻度,就是这个角的度数,依此解答。
【详解】此图中的角是30°,因为与这个角一条边与0°刻度线重合,另一边在量角器的30°刻度线上。
此图中,只看到角的一边在110°或70°的刻度线上,而没有看到角的另一边在哪一条刻度线上,因此这个角的度数无法确定,当角的另一边在左边的0°刻度线上时,此时这个角为110°;当角的另一边在右边的0°刻度线上时,此时这个角为70°,即这个角可能是110°,也可能是70°。
【点睛】熟练掌握用量角器测量角的度数的方法是解答此题的关键。
26.∠3=∠4
【分析】根据直角的定义,可知∠2+∠4=90°,∠1+∠3=90°,因为∠1=∠2,则∠4=∠3。
【详解】因为∠2+∠4=90°
∠1+∠3=90°
所以∠4=90°-∠2
∠3=90°-∠1
因为∠1=∠2
所以∠3=∠4
【点睛】解答本题的关键是明确直角的定义。
27.100;见解析
【分析】(1)用量角器的圆点和角的顶点重合,30°刻度线和角的一条边重合,另一条边在量角器上的刻度是130°,用130°减去30°就是该角的度数;
(2)150°-100°=50°,根据用量角器画角的方法,用量角器的圆点和角的顶点重合,100°刻度线和角的一条边重合,另一条边在量角器上的150°刻度线,据此画角即可。
【详解】(1)∠1=130°-30°=100°
(2)画图如下:
【点睛】熟练掌握用量角器画角的方法以及角的度量方法,是解答此题的关键。
28.(1)见详解
(2)锐;120;
【分析】(1)直线没有端点,是无限长的,因此用直尺过A点和B点画一条直的线,即可得到一条直线;
射线只有一个端点,因此以点B为端点,过C点画一条直的线即可得到一条射线;依此画图即可。
(2)量角的步骤是:先把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合,角的另一边所对的量角器上的刻度,就是这个角的度数,依此测量并根据角的分类标准填空即可。
【详解】(1)画图如下:
(2)根据测量可知,画好的图形中的两个角分别是60°和120°,因此画好的图形中有钝角和锐角,钝角是120度。
【点睛】解答此题的关键是要熟练掌握角的分类标准,角的度量方法,以及射线和直线的特点。
29.见详解
【分析】从一点出发画两条射线,就得到一个角,再用量角器测量出角的度数,标注在角上,根据角的度数判断是什么角。
【详解】
这个角的度数是110°,是钝角。
【点睛】本题主要考查学生对角的分类、画角、用量角器度量角的度数方法的掌握。
30.见详解过程
【分析】根据直线、射线和线段的含义:直线无端点,无限长,无法度量;射线有一个端点,无限长,无法度量;线段有限长,有两个端点,可以度量;进而进行判断即可。
【详解】直线有:(5);(7);
射线有:(1);(4);(6);
线段有:(2);(3);
相同之处:直线、射线和线段都是平面图形。
不同之处:直线无端点,无限长,无法度量;射线有一个端点,无限长,无法度量;线段有限长,有两个端点,可以度量。
【点睛】此题考查了直线、射线和线段的含义以及特点。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版四年级上册第三单元角的度量(知识点梳理+能力百分练)一
知识点梳理
1、线段、射线与直线的区别与联系:线段有两个端点,长度有限,不能延伸,可以测量;直线没有端点,无限长,向两端无限延伸,不可以测量;射线有一个端点,无限长,向一端无限延伸,不可以测量。直线和射线没有具体的长度.
2、线段、射线和直线的特点:经过一-点可以两无数条射线和直线,经过两点只能画一条直线。
3、角是从一点引出两条射线所组成的图形.所以它的两条边可以无限延伸,并不是边越长,角的度数越大。
4、角通常用符号“∠”表示,例如角1可以记作∠1.
5、角的计量单位是“度”,用符号“。”表示,将圆分成360等份,其中的1份所对的角是1度,记作1°。
6、使用量角器要做到“两合一看”。即把量角器的中心与角的顶点重合,0"刻度线与角的一条边重合,角的另一条边所对的量角器上的刻度,就是这个角的度数。
7、用三角尺可以画一些特殊度数的角,如30° ,60° ,90°等。
8、角分为五类:0°<锐角<90°、直角= 90°、90°<钝角< 180°、平角= 180°、周角= 360°。它们的大小关系是:锐角<直角<钝角<平角<周角。
能力百分练
一、选择题(共16分)
1.下面图形中,( )是射线。
A. B.
C. D.
2.下面关系中,正确的是( )。
A.1周角=4平角=2直角 B.1周角=2平角=3直角
C.1周角=2平角=4直角 D.1周角=3平角=4直角
3.用一副三角板不能拼出的角是( )。
A.75° B.120° C.150° D.160°
4.下面的各角中,可以用一副三角板画出来的是( )。
A.100° B.125° C.85° D.105°
5.破损的量角器也能测量角的大小。如图,这个角的度数是( )。
A.60° B.120° C.75° D.65°
6.下面是使用两块三角尺拼成的角,拼出的角是150°的是( )。
A. B. C. D.
7.下面的( )点,表示的是钝角。
A.A B.B C.C D.D
8.如图,两条直线相交,∠1=35°,下面说法错误的是( )。
A.∠1+∠2=180° B.∠1=∠3 C.∠3+∠4+∠5=180° D.∠3=∠5
二、填空题(共16分)
9.把5厘米长的线段向两端各延长10米,得到的是一条 。
10.把一个73°的角放在能放大10倍的放大镜下看,这个角的度数现在是( )。
11.用量角器量出角的度数。
∠1=( )。
12.把长方形的一个角折叠,如图所示。∠1=32°,那么∠2的度数是 。
13.如图,直线AB上共有( )条线段,( )条射线。
14.将一张圆形纸片对折3次后展开,相邻两条折痕所形成的角是( )度。
15.用一副三角尺拼出的最大钝角是( )度。
16.把一个平角分成两个角,如果其中一个角是锐角,那么另一个角是( )角。
三、判断题(共8分)
17.大于180°而小于90°的角是钝角。( )
18.角的边越短,角就越小。( )
19.如图,图中共有8个角。( )
20.奇思画了一条长0.2米的直线。( )
四、计算题(共6分)
21.(6分)求出下面各角的度数。
已知图中∠1=52°,求出∠2、∠3。
五、连线题(共6分)
22.(6分)红花配绿叶,连一连。
六、作图题(共12分)
23.(6分)用量角器画一个65°的角(保留作图痕迹)。
24.(6分)过点A画一条射线,并在射线上截取一条2厘米长的线段。
七、解答题(共36分)
25.(6分)你能猜出这几个角的度数吗?并说明原因。
26.(6分)如图所示,∠1=∠2,你能说明∠3和∠4相等吗?
27.(6分)图①中,用量角器量∠1的度数,∠1=______°;请你用类似的方法在图②量角器中画一个50°的角。
28.(6分)按要求画,再回答问题。
(1)画出直线AB,画出射线BC。
(2)画好的图形中有钝角和( )角,钝角是( )度。
29.(6分)任意画一个角,用量角器量出它的度数并写出是哪种角。
30.(6分)把下列线进行分类,找出各类线之间有什么相同和不同之处?
参考答案
1.C
【分析】把线段向一端无限延伸,就得到一条射线,射线只有一个端点,据此解答即可。
【详解】A.有两个端点,是线段;
B.从一点引出两条射线所组成的图形叫做角;
C.只有一个端点,是射线;
D.没有端点,是直线。
故答案为:C
【点睛】此题主要考查线段、直线、射线以及角的认识与特征。
2.C
【分析】周角等于360度,平角等于180度,直角等于90度,据此计算解答。
【详解】360°÷180°=2(个)
180°÷90°=2(个)
360°÷90°=4(个)
所以1周角=2平角=4直角。
故答案为:C
【点睛】本题考查了周角、平角及直角之间的关系。
3.D
【分析】一副三角板,其中一个三角板的角有30°、60°、90°,等腰直角三角板的角有45°、45°、90°,用它们进行拼组,即可解答。
【详解】A.30°+45°=75°,用一副三角板能拼出75°的角;
B.90°+30°=120°,用一副三角板能拼出120°的角;
C.90°+60°=150°,用一副三角板能拼出150°的角;
D.用一副三角板不能拼出160°的角。
故答案为:D
【点睛】本题考查了学生用一副三角板拼成不同角度的能力。
4.D
【分析】一副三角板中的各个角的度数分别是30°、60°、45°、90°。将它们进行组合,可得到的角有60°-45°=15°,60°+45°=105°,60°+90°=150°,90°+45°=135°,90°+30°=120°,30°+45°=75°,据此即可解答。
【详解】A.不可以用一副三角板拼成100°;
B.不可以用一副三角板拼成125°;
C.不可以用一副三角板拼成 85°;
D.60°+45°=105°,所以能用一副三角板拼成105°;
故答案为:D
【点睛】本题考查了学生用一副三角尺拼成角度情况的掌握,能用一副三角尺画出的角都是15°的整数倍。
5.D
【分析】根据图示,量角器显示这个角在75°和140°之间,利用大度数减小度数即可得到角的度数。
【详解】140°-75°=65°
这个角的度数是65°。
故答案为:D
【点睛】本题主要考查学生利用量角器测量角的度数的能力。
6.B
【分析】一副三角尺中的各个角的度数分别是30°、60°、45°、90°,求拼出的角的度数,把两个角的度数相加即可。
【详解】A.60°+45°=105°
B.60°+90°=150°
C.90°+30°=120°
D.90°+90°=180°
所以拼出的角是150°的是。
故答案为:B
【点睛】本题主要考查图形的拼组,关键是利用三角尺各角的度数解答。
7.B
【分析】钝角指的是角度大于90°小于180°的角,据此即可解答。
【详解】从图中可以看出A小于90°,C、D大于180°,B处在90°到180°之间。
故答案为:B
【点睛】本题考查的是角度的分类,弄清钝角的概念是关键。
8.D
【分析】根据题图可知,∠1和∠2组成一个平角,则∠1+∠2=180°。∠2和∠3组成一个平角,则∠2+∠3=180°。也就是∠1=∠3。∠3、∠4和∠5组成一个平角,则∠3+∠4+∠5=180°。∠1和∠5组成一个直角,则∠5=90°-∠1,而∠1=∠3,则∠3≠∠5。
【详解】A.∠1+∠2=180°,说法正确;
B.∠1=∠3=180°-∠2,说法正确;
C.∠3+∠4+∠5=180°,说法正确;
D.∠3=∠1=35°,∠5=90°-∠1=90°-35°=55°,则∠3≠∠5。说法错误。
故答案为:D
【点睛】解决此类问题时,要善于利用图中隐藏的特殊角(直角、平角、周角),以及它与各角之间的关系,利用已知角,求出未知角。
9.线段
【分析】根据线段的含义:线段有两个端点,有限长;据此解答即可。
【详解】把5厘米长的线段向两端各延长10米,得到的是一条线段。
【点睛】此题考查了线段的含义,应注意理解和掌握。
10.73°/73度
【分析】用放大镜看角时,放大的是角的边,不改变角的形状和大小,据此解答。
【详解】把一个73°的角放在能放大10倍的放大镜下看,这个角的度数现在是73°。
【点睛】本题主要考查角的度量,解题关键是正确掌握放大镜的特性,只改变边的长度,而不能改变角的开口大小。
11.50°
【分析】用量角器度量角的方法是:把量角器的中心与角的顶点重合,0刻度线与边的一边重合,角的另一边所经过的量角器上所显示的刻度就是被量角的度数。
【详解】用量角器量出角的度数,∠1=50°。
【点睛】用量角器量角要做“两重合”,“一看准”。“两重合”是先把量角器的中心与角的顶点重重合;把量角器的零刻度线与角的一边重合;“一看准”是指最后看角的另一边所对的量角器上的刻度,就是所量的角的度数。
12.26°
【分析】长方形的4个角都是直角。将一个角折叠后,∠1盖住了一个与它度数相等的角,也就是2∠1与∠2的和是90°,∠2=90°-2×∠1,据此解答。
【详解】∠2=90°-32×2°
=90°-64°
=26°
【点睛】解决此类问题时,要善于利用图中隐藏的特殊角(直角、平角、周角),以及它与各角之间的关系,利用已知角,求出未知角。
13. 6 8
【分析】由题目可知,从短到长,线段共有(3+2+1)条,每个端点发出两条射线,所以共8条射线,即可解题。
【详解】由分析可知:
3+2+1=6(条)
所以直线AB上共有6条线段,8条射线。
【点睛】此题主要考查了线段和射线的定义,要熟练掌握。
14.45
【分析】一张圆形的纸片,圆心角是360度,对折一次,就是把圆心角平均分成2份,得到两个180度的平角,再对折一次就把平角再平均分成2个一样的90度直角,再对折又把直角平均分成了45度的角,据此解答。
【详解】如图所示:
360÷2÷2÷2
=180÷2÷2
=90÷2
=45(度)
将一张圆形纸片对折3次后展开,相邻两条折痕所形成的角是45度。
【点睛】本题考查了周角、平角及直角的认识。解答此题时,可亲自动手操作一下。
15.150
【分析】一副三角尺有两个直角三角板,其中一个直角三角板的角度数分别是30度,60度,90度,另一个直角三角板的角度数分别是45度,45度,90度,结合钝角是大于90度且小于180度的角,即可解答。
【详解】根据分析可知,用一副三角尺能够拼出的钝角有:
30+90=120(度)
60+45=105(度)
60+90=150(度)
所以用一副三角尺拼出的最大钝角是150度。
【点睛】本题主要考查用三角板拼角和角的分类,属于基础知识,要熟练掌握。
16.钝
【分析】根据锐角、直角、钝角、平角的意义,小于90度的角叫做锐角;等于90度的角叫做直角;大于90度小于180度的角叫做钝角,等于180度的角叫做平角,据此解答即可。
【详解】由分析可知:平角=锐角+钝角,所以把一个平角分成两个角,如果其中一个角是锐角,那么另一个角一定是钝角。
【点睛】此题考查的目的是理解掌握锐角、直角、钝角、平角的意义,需熟练掌握。
17.×
【详解】
如图所示,∠1是一个钝角。小于180°大于90°的角是钝角,题干说法错误。
故答案为:×
18.×
【分析】根据角的概念:由一点引出的两条射线所围成的图形,叫做角;角的大小与两条边的长短(射线,无限长)无关,只与开口的大小有关;进而判断即可。
【详解】由分析可知:角的大小只与开口的大小有关,与两条边的长短无关;所以原题的说法错误。
故答案为:×
【点睛】此题考查了角的概念和影响角的大小的因素。
19.×
【分析】图中5条射线,每相邻两条射线组成1个小角,这样的小角有4个,每相邻两个小角合成1个角,这样的角有3个,相邻三个小角合成一个角,这样的角有2个,全部4个小角合成1个角;据此解答即可。
【详解】1+2+3+4
=3+3+4
=6+4
=10(个)
所以,图中共有10个角,故原题说法错误。
故答案为:×
【点睛】此题重点考查在多个角组成的组合图形中计角个数的方法。
20.×
【分析】一根拉紧的线、紧绷的弦都可以看作线段,线段有两个端点,可以测量出长度;把线段向两端无限延伸就可以得到一条直线,直线没有端点,是无限长的,因此不可以测量出长度,依此判断。
【详解】奇思画了一条长0.2米的线段,原题干说法错误。
故答案为:×
【点睛】熟练掌握直线、线段的特点是解答此题的关键。
21.∠2=38°;∠3=142°
【分析】1直角=90°,1平角=180°,根据题意可知:∠1+∠2+90°=180°,因此∠2=180°-90°-∠1;∠3+∠2=180°,因此∠3=180°-∠2;依此计算。
【详解】∠2=180°-90°-52°=90°-52°=38°;
∠3=180°-38°=142°。
即∠2=38°,∠3=142°。
22.见详解
【分析】根据锐角、钝角、直角、平角、周角的含义可知:锐角是大于0°小于90°的角;钝角是大于90°小于180°的角;直角是等于90°的角;平角是等于180°的角;周角是等于360°的角;据此连线即可。
【详解】
【点睛】熟悉锐角、直角、钝角、平角、周角的度数范围是解答此题的关键。
23.见详解
【分析】画一条射线,使量角器的中心和射线的端点重合,0°刻度线和射线重合。在量角器65°刻度线的地方点一个点。以画出的射线的端点为端点,通过刚画的点,再画一条射线。据此画出65°的角。
【详解】
【点睛】本题考查用量角器画角的方法。画角注意两重和,量角器的中心和射线的端点重合,0°刻度线和射线重合。
24.见解答
【分析】射线只有一个端点,因此以点A为端点向一边画一条直的线即可得到一条射线;
线段有两个端点,因此可以以A点为线段的一个端点,并且使A点对准直尺的0刻度线,直尺紧靠所画的射线,2厘米处就是这条线段的另一个端点,依此画图即可。
【详解】画图如下:
【点睛】熟练掌握射线、线段的特点,是解答此题的关键。
25.30°;可能是110°或70°(原因见详解)
【分析】量角的步骤是:先把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合,角的另一边所对的量角器上的刻度,就是这个角的度数,依此解答。
【详解】此图中的角是30°,因为与这个角一条边与0°刻度线重合,另一边在量角器的30°刻度线上。
此图中,只看到角的一边在110°或70°的刻度线上,而没有看到角的另一边在哪一条刻度线上,因此这个角的度数无法确定,当角的另一边在左边的0°刻度线上时,此时这个角为110°;当角的另一边在右边的0°刻度线上时,此时这个角为70°,即这个角可能是110°,也可能是70°。
【点睛】熟练掌握用量角器测量角的度数的方法是解答此题的关键。
26.∠3=∠4
【分析】根据直角的定义,可知∠2+∠4=90°,∠1+∠3=90°,因为∠1=∠2,则∠4=∠3。
【详解】因为∠2+∠4=90°
∠1+∠3=90°
所以∠4=90°-∠2
∠3=90°-∠1
因为∠1=∠2
所以∠3=∠4
【点睛】解答本题的关键是明确直角的定义。
27.100;见解析
【分析】(1)用量角器的圆点和角的顶点重合,30°刻度线和角的一条边重合,另一条边在量角器上的刻度是130°,用130°减去30°就是该角的度数;
(2)150°-100°=50°,根据用量角器画角的方法,用量角器的圆点和角的顶点重合,100°刻度线和角的一条边重合,另一条边在量角器上的150°刻度线,据此画角即可。
【详解】(1)∠1=130°-30°=100°
(2)画图如下:
【点睛】熟练掌握用量角器画角的方法以及角的度量方法,是解答此题的关键。
28.(1)见详解
(2)锐;120;
【分析】(1)直线没有端点,是无限长的,因此用直尺过A点和B点画一条直的线,即可得到一条直线;
射线只有一个端点,因此以点B为端点,过C点画一条直的线即可得到一条射线;依此画图即可。
(2)量角的步骤是:先把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合,角的另一边所对的量角器上的刻度,就是这个角的度数,依此测量并根据角的分类标准填空即可。
【详解】(1)画图如下:
(2)根据测量可知,画好的图形中的两个角分别是60°和120°,因此画好的图形中有钝角和锐角,钝角是120度。
【点睛】解答此题的关键是要熟练掌握角的分类标准,角的度量方法,以及射线和直线的特点。
29.见详解
【分析】从一点出发画两条射线,就得到一个角,再用量角器测量出角的度数,标注在角上,根据角的度数判断是什么角。
【详解】
这个角的度数是110°,是钝角。
【点睛】本题主要考查学生对角的分类、画角、用量角器度量角的度数方法的掌握。
30.见详解过程
【分析】根据直线、射线和线段的含义:直线无端点,无限长,无法度量;射线有一个端点,无限长,无法度量;线段有限长,有两个端点,可以度量;进而进行判断即可。
【详解】直线有:(5);(7);
射线有:(1);(4);(6);
线段有:(2);(3);
相同之处:直线、射线和线段都是平面图形。
不同之处:直线无端点,无限长,无法度量;射线有一个端点,无限长,无法度量;线段有限长,有两个端点,可以度量。
【点睛】此题考查了直线、射线和线段的含义以及特点。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
