2007年优等生中考复习练习(1)无答案(浙江省宁波市)
文档属性
| 名称 | 2007年优等生中考复习练习(1)无答案(浙江省宁波市) |
|
|
| 格式 | rar | ||
| 文件大小 | 228.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-06-11 00:00:00 | ||
图片预览

文档简介
2007年第一学期夜课甲班练习(2) 姓名:____________
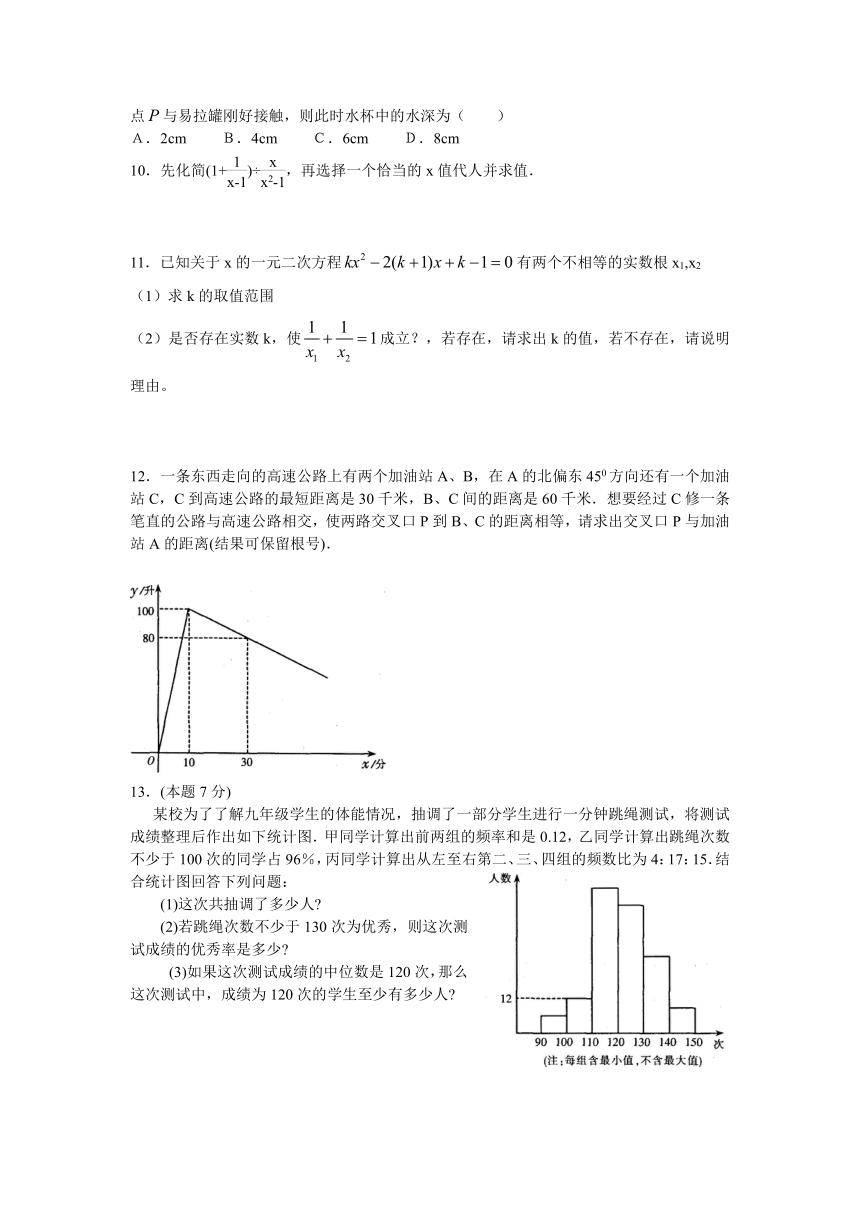
1.如图,用灰白两色正方形瓷砖铺设地面,第个图案中白色瓷砖块数为_________.
2.由表格中信息可知,若设,则下列y与x之间的函数关系式正确的是( )
-1 0 1
ax2 1
ax2+bx+c 8 3
A. B.
C. D.
3.如图,按英语字母表A,B,C,,D,E,F,G,H,,的顺序有规律排列而成的鱼状图案中,字母“G”出现的个数为_______.
4.把一副三角板按如图方式放置,则两条斜边所形成的钝角α=_______度.
5.如图,把一个长方体的礼品盒用丝带打上包装,打蝴蝶结部分需丝带45cm.那么打好整个包装所用丝带总长为_______cm.
6.把-1,0,1,2,3这五个数,填入下列方框中,使行、列三个数的和相等,其中错误的是( )
7.下列由数字组成的图形中,是轴对称图形的是( )
8.如图,把边长为的正方形的局部进行图①~图④的变换,拼成图⑤,则图⑤的面积是( )
A.18 B.16 C.12 D.8
9.如图,在把易拉罐中的水倒入一个圆水杯的过程中,若水杯中的水在点与易拉罐刚好接触,则此时水杯中的水深为( )
A.2cm B.4cm C.6cm D.8cm
10.先化简(1+)÷,再选择一个恰当的x值代人并求值.
11.已知关于x的一元二次方程有两个不相等的实数根x1,x2
(1)求k的取值范围
(2)是否存在实数k,使成立?,若存在,请求出k的值,若不存在,请说明理由。
12.一条东西走向的高速公路上有两个加油站A、B,在A的北偏东450方向还有一个加油站C,C到高速公路的最短距离是30千米,B、C间的距离是60千米.想要经过C修一条笔直的公路与高速公路相交,使两路交叉口P到B、C的距离相等,请求出交叉口P与加油站A的距离(结果可保留根号).
13.(本题7分)
某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题:
(1)这次共抽调了多少人
(2)若跳绳次数不少于130次为优秀,则这次测试成绩的优秀率是多少
(3)如果这次测试成绩的中位数是120次,那么这次测试中,成绩为120次的学生至少有多少人
14.如图①,有两个形状完全相同的直角三角形ABC和EFG叠放在一起(点A与点E重合),已知AC=8cm,BC=6cm,∠C=90°,EG=4cm,∠EGF=90°,O 是△EFG斜边上的中点.
如图②,若整个△EFG从图①的位置出发,以1cm/s 的速度沿射线AB方向平移,在△EFG 平移的同时,点P从△EFG的顶点G出发,以1cm/s 的速度在直角边GF上向点F运动,当点P到达点F时,点P停止运动,△EFG也随之停止平移.设运动时间为x(s),FG的延长线交 AC于H,四边形OAHP的面积为y(cm2)(不考虑点P与G、F重合的情况).
(1)当x为何值时,OP∥AC
(2)求y与x 之间的函数关系式,并确定自变量x的取值范围.
(3)是否存在某一时刻,使四边形OAHP面积与△ABC面积的比为13∶24?若存在,求出x的值;若不存在,说明理由.
(参考数据:1142 =12996,1152 =13225,1162 =13456
或4.42 =19.36,4.52 =20.25,4.62 =21.16)
15.如图,以O为原点的直角坐标系中,A点的坐标为(0,1),直线x=1交x轴于点B。P为线段AB上一动点,作直线PC⊥PO,交直线x=1于点C。过P点作直线MN平行于x轴,交y轴于点M,交直线x=1于点N。
(1)当点C在第一象限时,求证:△OPM≌△PCN;
(2)当点C在第一象限时,设AP长为m,四边形POBC的面积为S,请求出S与m间的函数关系式,并写出自变量m的取值范围;
(3)当点P在线段AB上移动时,点C也随之在直线x=1上移动,△PBC是否可能成为等腰三角形?如果可能,求出所有能使△PBC成为等腰直角三角形的点P的坐标;如果不可能,请说明理由。
16.如图,已知抛物线与坐标轴的交点依次是,,.
(1)求抛物线关于原点对称的抛物线的解析式;
(2)设抛物线的顶点为,抛物线与轴分别交于两点(点在点的左侧),顶点为,四边形的面积为.若点,点同时以每秒1个单位的速度沿水平方向分别向右、向左运动;与此同时,点,点同时以每秒2个单位的速度沿坚直方向分别向下、向上运动,直到点与点重合为止.求出四边形的面积与运动时间之间的关系式,并写出自变量的取值范围;
(3)当为何值时,四边形的面积有最大值,并求出此最大值;
(4)在运动过程中,四边形能否形成矩形?若能,求出此时的值;若不能,请说明理由.
17.南博汽车城销售某种型号的汽车,每辆进货价为25万元,市场调研表明:当销售价为29万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价万元,每辆汽车的销售利润为万元.(销售利润销售价进货价)
(1)求与的函数关系式;在保证商家不亏本的前提下,写出的取值范围;
(2)假设这种汽车平均每周的销售利润为万元,试写出与之间的函数关系式;
(3)当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少?
18.已知两个关于的二次函数与
;当时,;且二次函数的图象的对称轴是直线.
(1)求的值;
(2)求函数的表达式;
(3)在同一直角坐标系内,问函数的图象与的图象是否有交点?请说明理由.
第1个图案
第2个图案
第3个图案
A
B
C
N
P
M
O
x
y
x=1
1.如图,用灰白两色正方形瓷砖铺设地面,第个图案中白色瓷砖块数为_________.
2.由表格中信息可知,若设,则下列y与x之间的函数关系式正确的是( )
-1 0 1
ax2 1
ax2+bx+c 8 3
A. B.
C. D.
3.如图,按英语字母表A,B,C,,D,E,F,G,H,,的顺序有规律排列而成的鱼状图案中,字母“G”出现的个数为_______.
4.把一副三角板按如图方式放置,则两条斜边所形成的钝角α=_______度.
5.如图,把一个长方体的礼品盒用丝带打上包装,打蝴蝶结部分需丝带45cm.那么打好整个包装所用丝带总长为_______cm.
6.把-1,0,1,2,3这五个数,填入下列方框中,使行、列三个数的和相等,其中错误的是( )
7.下列由数字组成的图形中,是轴对称图形的是( )
8.如图,把边长为的正方形的局部进行图①~图④的变换,拼成图⑤,则图⑤的面积是( )
A.18 B.16 C.12 D.8
9.如图,在把易拉罐中的水倒入一个圆水杯的过程中,若水杯中的水在点与易拉罐刚好接触,则此时水杯中的水深为( )
A.2cm B.4cm C.6cm D.8cm
10.先化简(1+)÷,再选择一个恰当的x值代人并求值.
11.已知关于x的一元二次方程有两个不相等的实数根x1,x2
(1)求k的取值范围
(2)是否存在实数k,使成立?,若存在,请求出k的值,若不存在,请说明理由。
12.一条东西走向的高速公路上有两个加油站A、B,在A的北偏东450方向还有一个加油站C,C到高速公路的最短距离是30千米,B、C间的距离是60千米.想要经过C修一条笔直的公路与高速公路相交,使两路交叉口P到B、C的距离相等,请求出交叉口P与加油站A的距离(结果可保留根号).
13.(本题7分)
某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题:
(1)这次共抽调了多少人
(2)若跳绳次数不少于130次为优秀,则这次测试成绩的优秀率是多少
(3)如果这次测试成绩的中位数是120次,那么这次测试中,成绩为120次的学生至少有多少人
14.如图①,有两个形状完全相同的直角三角形ABC和EFG叠放在一起(点A与点E重合),已知AC=8cm,BC=6cm,∠C=90°,EG=4cm,∠EGF=90°,O 是△EFG斜边上的中点.
如图②,若整个△EFG从图①的位置出发,以1cm/s 的速度沿射线AB方向平移,在△EFG 平移的同时,点P从△EFG的顶点G出发,以1cm/s 的速度在直角边GF上向点F运动,当点P到达点F时,点P停止运动,△EFG也随之停止平移.设运动时间为x(s),FG的延长线交 AC于H,四边形OAHP的面积为y(cm2)(不考虑点P与G、F重合的情况).
(1)当x为何值时,OP∥AC
(2)求y与x 之间的函数关系式,并确定自变量x的取值范围.
(3)是否存在某一时刻,使四边形OAHP面积与△ABC面积的比为13∶24?若存在,求出x的值;若不存在,说明理由.
(参考数据:1142 =12996,1152 =13225,1162 =13456
或4.42 =19.36,4.52 =20.25,4.62 =21.16)
15.如图,以O为原点的直角坐标系中,A点的坐标为(0,1),直线x=1交x轴于点B。P为线段AB上一动点,作直线PC⊥PO,交直线x=1于点C。过P点作直线MN平行于x轴,交y轴于点M,交直线x=1于点N。
(1)当点C在第一象限时,求证:△OPM≌△PCN;
(2)当点C在第一象限时,设AP长为m,四边形POBC的面积为S,请求出S与m间的函数关系式,并写出自变量m的取值范围;
(3)当点P在线段AB上移动时,点C也随之在直线x=1上移动,△PBC是否可能成为等腰三角形?如果可能,求出所有能使△PBC成为等腰直角三角形的点P的坐标;如果不可能,请说明理由。
16.如图,已知抛物线与坐标轴的交点依次是,,.
(1)求抛物线关于原点对称的抛物线的解析式;
(2)设抛物线的顶点为,抛物线与轴分别交于两点(点在点的左侧),顶点为,四边形的面积为.若点,点同时以每秒1个单位的速度沿水平方向分别向右、向左运动;与此同时,点,点同时以每秒2个单位的速度沿坚直方向分别向下、向上运动,直到点与点重合为止.求出四边形的面积与运动时间之间的关系式,并写出自变量的取值范围;
(3)当为何值时,四边形的面积有最大值,并求出此最大值;
(4)在运动过程中,四边形能否形成矩形?若能,求出此时的值;若不能,请说明理由.
17.南博汽车城销售某种型号的汽车,每辆进货价为25万元,市场调研表明:当销售价为29万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价万元,每辆汽车的销售利润为万元.(销售利润销售价进货价)
(1)求与的函数关系式;在保证商家不亏本的前提下,写出的取值范围;
(2)假设这种汽车平均每周的销售利润为万元,试写出与之间的函数关系式;
(3)当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少?
18.已知两个关于的二次函数与
;当时,;且二次函数的图象的对称轴是直线.
(1)求的值;
(2)求函数的表达式;
(3)在同一直角坐标系内,问函数的图象与的图象是否有交点?请说明理由.
第1个图案
第2个图案
第3个图案
A
B
C
N
P
M
O
x
y
x=1
同课章节目录
