2007年优等生中考复习练习(4)无答案(浙江省宁波市)
文档属性
| 名称 | 2007年优等生中考复习练习(4)无答案(浙江省宁波市) |  | |
| 格式 | rar | ||
| 文件大小 | 144.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-06-11 13:07:00 | ||
图片预览

文档简介
2007年第一学期夜课甲班练习(4) 姓名:____________
1.将下列各纸片沿虚线剪开后,能拼成右图的是( )
2.不等式组的解集为( )
A.-1<x<2 B.-1<x≤2 C.x<-1 D.x≥2
3.锦州市宝石广场占地面积约为12555米2,它的面积与一个班级教师面积的倍数关系,
下列最接近的是( )
A.40倍 B.80倍 C.100倍 D.150倍
4.如图是水滴入一个玻璃容器的示意图(滴水速度保持不变),下列图象能正确反映容器中水的高度(h)与时间(t)之间函数关系的是( )
5.若多项式4a2+M能用平方差公式分解因式,则单项式M=____(写出一个即可).
6.已知二次函数的图象开口向上,且顶点在y轴的负半轴上,请你写出一个满足条件的二次函数的表达式____.
7.如图,将边长为a的正方形ABCD沿直线l按顺时针方向翻滚,当正方形翻滚一周时,正方形的中心O所经过的路径长为____.
8.下面的两个网格中,每个小正方形的边长均为.请你分别在每个网格中画出一个顶点在格点上,且周长为的形状和大小不同的凸多边形.
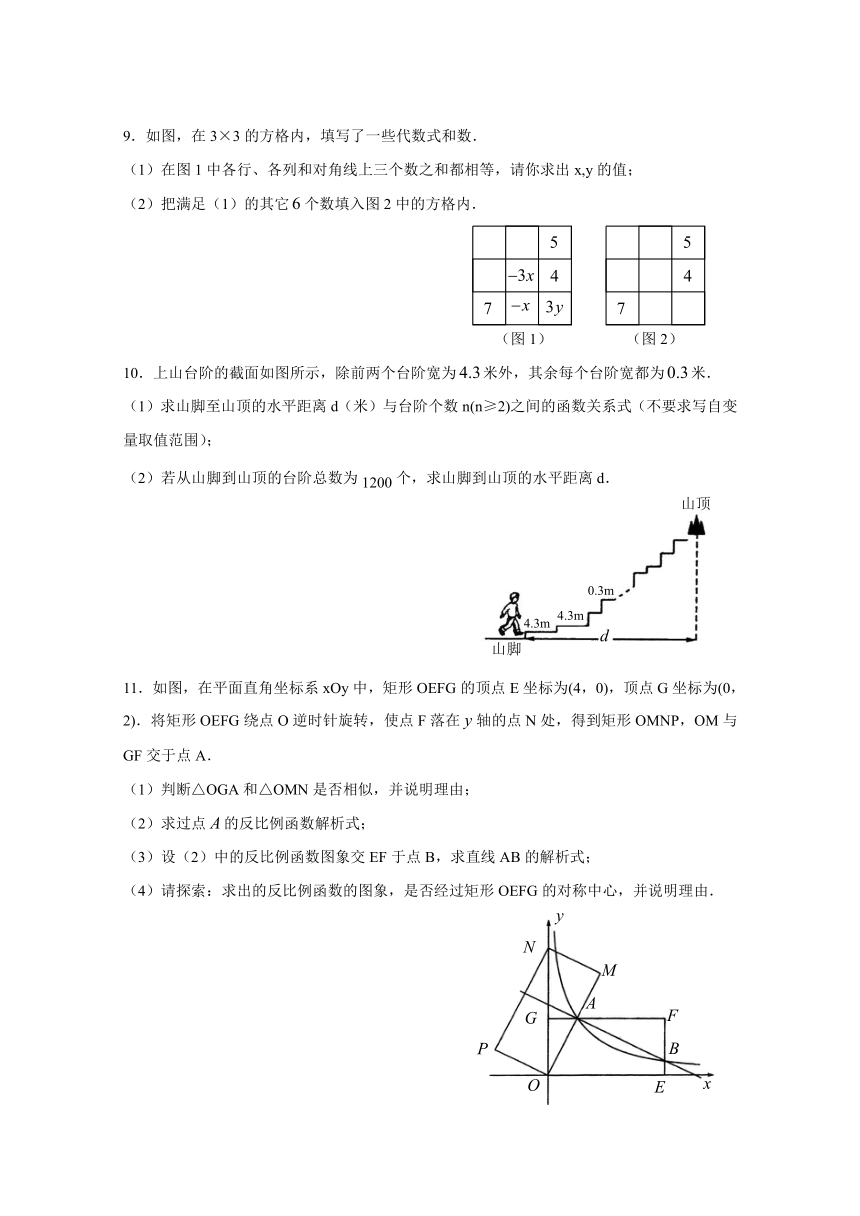
9.如图,在3×3的方格内,填写了一些代数式和数.
(1)在图1中各行、各列和对角线上三个数之和都相等,请你求出x,y的值;
(2)把满足(1)的其它个数填入图2中的方格内.
10.上山台阶的截面如图所示,除前两个台阶宽为米外,其余每个台阶宽都为米.
(1)求山脚至山顶的水平距离d(米)与台阶个数n(n≥2)之间的函数关系式(不要求写自变量取值范围);
(2)若从山脚到山顶的台阶总数为1200个,求山脚到山顶的水平距离d.
11.如图,在平面直角坐标系xOy中,矩形OEFG的顶点E坐标为(4,0),顶点G坐标为(0,2).将矩形OEFG绕点O逆时针旋转,使点F落在轴的点N处,得到矩形OMNP,OM与GF交于点A.
(1)判断△OGA和△OMN是否相似,并说明理由;
(2)求过点的反比例函数解析式;
(3)设(2)中的反比例函数图象交EF于点B,求直线AB的解析式;
(4)请探索:求出的反比例函数的图象,是否经过矩形OEFG的对称中心,并说明理由.
12.如图,在边长为8厘米的正方形内,贴上一个边长为4厘米的正方形AEFG,正方形ABCD未被盖住的部分为多边形EBCDGF.动点P从点B出发,沿B→C→D方向以厘米/秒速度运动,到点D停止,连结PA,PE.设点P运动x秒后,△APE与多边形EBCDGF重叠部分的面积为y厘米2.
(1)当x=5时,求y的值;
(2)当x=10时,求y的值;
(3)求y与x之间的函数关系式;
(4)在给出的直角坐标系中画出与之间的函数图象.
13.小明受《乌鸦喝水》故事的启发,利用量桶和体积相同的小球进行了如下操作:
请根据图中给出的信息,解答下列问题:
(1)放入一个小球量桶中水面升高___________;
(2)求放入小球后量桶中水面的高度y(cm)与小球个数x(个)之间的一次函数关系式(不要求写出自变量的取值范围);
(3)量桶中至少放入几个小球时有水溢出?
14.如图,在平面直角坐标系xOy中,把矩形COAB绕点C顺时针旋转α角,得到矩形CFED.设FC与AB交于点H,且A(0,4),C(6,0)(如图1).
(1)当α=60°时,△CBD的形状是_____________;
(2)当AH=HC时,求直线FC的解析式;
(3)当α=90°时,(如图2).请探究:经过点D,且以点B为顶点的抛物线,是否经过矩形CFED的对称中心M,并说明理由.
15.如图,正方形ABCD的边长为2cm,在对称中心O处有一钉子.动点P,Q同时从点A出发,点P沿节A→B→C方向以每秒的速度运动,到点C停止,点Q沿A→D方向以每秒1cm的速度运动,到点D停止.P,Q两点用一条可伸缩的细橡皮筋联结,设x秒后橡皮筋扫过的面积为ycm2.
(1)当0≤x≤1时,求y与x之间的函数关系式;
(2)当橡皮筋刚好触及钉子时,求x值;
(3)当1≤x≤2时,求y与x之间的函数关系式,并写出橡皮筋从触及钉子到运动停止时∠POQ的变化范围;
(4)当0≤x≤2时,请在给出的直角坐标系中画出与之间的函数图象.
(图1)
(图2)
山脚
4.3m
4.3m
0.3m
山顶
(备用图)
(备用图)
1.将下列各纸片沿虚线剪开后,能拼成右图的是( )
2.不等式组的解集为( )
A.-1<x<2 B.-1<x≤2 C.x<-1 D.x≥2
3.锦州市宝石广场占地面积约为12555米2,它的面积与一个班级教师面积的倍数关系,
下列最接近的是( )
A.40倍 B.80倍 C.100倍 D.150倍
4.如图是水滴入一个玻璃容器的示意图(滴水速度保持不变),下列图象能正确反映容器中水的高度(h)与时间(t)之间函数关系的是( )
5.若多项式4a2+M能用平方差公式分解因式,则单项式M=____(写出一个即可).
6.已知二次函数的图象开口向上,且顶点在y轴的负半轴上,请你写出一个满足条件的二次函数的表达式____.
7.如图,将边长为a的正方形ABCD沿直线l按顺时针方向翻滚,当正方形翻滚一周时,正方形的中心O所经过的路径长为____.
8.下面的两个网格中,每个小正方形的边长均为.请你分别在每个网格中画出一个顶点在格点上,且周长为的形状和大小不同的凸多边形.
9.如图,在3×3的方格内,填写了一些代数式和数.
(1)在图1中各行、各列和对角线上三个数之和都相等,请你求出x,y的值;
(2)把满足(1)的其它个数填入图2中的方格内.
10.上山台阶的截面如图所示,除前两个台阶宽为米外,其余每个台阶宽都为米.
(1)求山脚至山顶的水平距离d(米)与台阶个数n(n≥2)之间的函数关系式(不要求写自变量取值范围);
(2)若从山脚到山顶的台阶总数为1200个,求山脚到山顶的水平距离d.
11.如图,在平面直角坐标系xOy中,矩形OEFG的顶点E坐标为(4,0),顶点G坐标为(0,2).将矩形OEFG绕点O逆时针旋转,使点F落在轴的点N处,得到矩形OMNP,OM与GF交于点A.
(1)判断△OGA和△OMN是否相似,并说明理由;
(2)求过点的反比例函数解析式;
(3)设(2)中的反比例函数图象交EF于点B,求直线AB的解析式;
(4)请探索:求出的反比例函数的图象,是否经过矩形OEFG的对称中心,并说明理由.
12.如图,在边长为8厘米的正方形内,贴上一个边长为4厘米的正方形AEFG,正方形ABCD未被盖住的部分为多边形EBCDGF.动点P从点B出发,沿B→C→D方向以厘米/秒速度运动,到点D停止,连结PA,PE.设点P运动x秒后,△APE与多边形EBCDGF重叠部分的面积为y厘米2.
(1)当x=5时,求y的值;
(2)当x=10时,求y的值;
(3)求y与x之间的函数关系式;
(4)在给出的直角坐标系中画出与之间的函数图象.
13.小明受《乌鸦喝水》故事的启发,利用量桶和体积相同的小球进行了如下操作:
请根据图中给出的信息,解答下列问题:
(1)放入一个小球量桶中水面升高___________;
(2)求放入小球后量桶中水面的高度y(cm)与小球个数x(个)之间的一次函数关系式(不要求写出自变量的取值范围);
(3)量桶中至少放入几个小球时有水溢出?
14.如图,在平面直角坐标系xOy中,把矩形COAB绕点C顺时针旋转α角,得到矩形CFED.设FC与AB交于点H,且A(0,4),C(6,0)(如图1).
(1)当α=60°时,△CBD的形状是_____________;
(2)当AH=HC时,求直线FC的解析式;
(3)当α=90°时,(如图2).请探究:经过点D,且以点B为顶点的抛物线,是否经过矩形CFED的对称中心M,并说明理由.
15.如图,正方形ABCD的边长为2cm,在对称中心O处有一钉子.动点P,Q同时从点A出发,点P沿节A→B→C方向以每秒的速度运动,到点C停止,点Q沿A→D方向以每秒1cm的速度运动,到点D停止.P,Q两点用一条可伸缩的细橡皮筋联结,设x秒后橡皮筋扫过的面积为ycm2.
(1)当0≤x≤1时,求y与x之间的函数关系式;
(2)当橡皮筋刚好触及钉子时,求x值;
(3)当1≤x≤2时,求y与x之间的函数关系式,并写出橡皮筋从触及钉子到运动停止时∠POQ的变化范围;
(4)当0≤x≤2时,请在给出的直角坐标系中画出与之间的函数图象.
(图1)
(图2)
山脚
4.3m
4.3m
0.3m
山顶
(备用图)
(备用图)
同课章节目录
