2007年优等生中考复习练习(5)无答案(浙江省宁波市)
文档属性
| 名称 | 2007年优等生中考复习练习(5)无答案(浙江省宁波市) |
|
|
| 格式 | rar | ||
| 文件大小 | 91.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-06-11 00:00:00 | ||
图片预览


文档简介
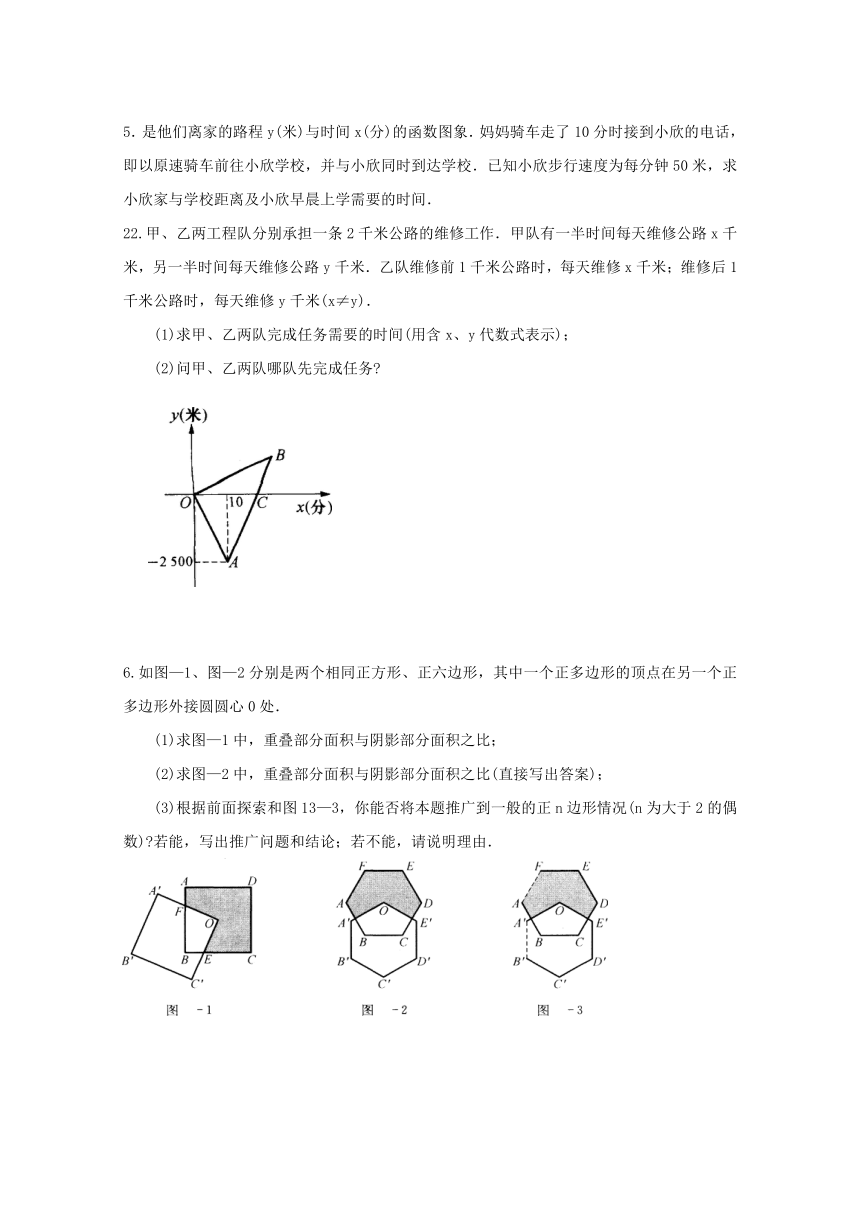
2007年第一学期夜课甲班练习(5) 姓名:____________
1.点P是△ABC中AB边上的一点,过点P作直线(不与直线AB重合)截△ABC,使截得的三角形与△ABC相似.满足这样条件的直线最多有____条.
2.如图,在梯形ABCD中,AD∥BC,AD=a,BC=b.若E1、F1分别是AB、DC的中点,则;若分别是的中点,则;当分别是的中点,则;若分别是的中点,根据上述规律猜想EnFn=____(n≥1,n为整数).
3.小张骑车往返于甲、乙两地,距甲地的路程y(千米)与时间x(小时)的函数图象如图所示.
(1)小张在路上停留 小时,他从乙地返回时骑车的速度为 千米/时.
(2)小李与小张同时从甲地出发,按相同路线匀速前往乙地,到乙地停止,途中小李与小张共相遇3次.请在图中画出小李距甲地的路程(千米)与时间(小时)的函数的大致图象.
(3)小王与小张同时出发,按相同路线前往乙地,距甲地的路程(千米)与时间(小时)的函数关系式为y=12x+10.小王与小张在途中共相遇几次?请你计算第一次相遇的时间.
4.如图①,正方形ABCD的顶点A,B的坐标分别为,顶点C,D在第一象限.点P从点A出发,沿正方形按逆时针方向匀速运动,同时,点Q从点E(4,0)出发,沿x轴正方向以相同速度运动.当点P到达点C时,P,Q两点同时停止运动,设运动的时间为t秒.
(1)求正方形ABCD的边长.
(2)当点P在AB边上运动时,△OPQ的面积S(平方单位)与时间t(秒)之间的函数图象为抛物线的一部分(如图②所示),求P,Q两点的运动速度.
(3)求(2)中面积S(平方单位)与时间t(秒)的函数关系式及面积取最大值时点的坐标.
(4)若点P,Q保持(2)中的速度不变,则点P沿着AB边运动时,∠OPQ的大小随着时间的增大而增大;沿着BC边运动时,∠OPQ的大小随着时间的增大而减小.当点沿着这两边运动时,使∠OPQ=90°的点有 个.
5.是他们离家的路程y(米)与时间x(分)的函数图象.妈妈骑车走了10分时接到小欣的电话,即以原速骑车前往小欣学校,并与小欣同时到达学校.已知小欣步行速度为每分钟50米,求小欣家与学校距离及小欣早晨上学需要的时间.
22.甲、乙两工程队分别承担一条2千米公路的维修工作.甲队有一半时间每天维修公路x千米,另一半时间每天维修公路y千米.乙队维修前1千米公路时,每天维修x千米;维修后1千米公路时,每天维修y千米(x≠y).
(1)求甲、乙两队完成任务需要的时间(用含x、y代数式表示);
(2)问甲、乙两队哪队先完成任务
6.如图—1、图—2分别是两个相同正方形、正六边形,其中一个正多边形的顶点在另一个正多边形外接圆圆心0处.
(1)求图—1中,重叠部分面积与阴影部分面积之比;
(2)求图—2中,重叠部分面积与阴影部分面积之比(直接写出答案);
(3)根据前面探索和图13—3,你能否将本题推广到一般的正n边形情况(n为大于2的偶数) 若能,写出推广问题和结论;若不能,请说明理由.
7.小明为了通过描点法作出函数y=x2-x+1的图象,先取自变量x的7个值满足:x2-x1=x3-x2=…=x7-x6=d,再分别算出对应的y值,列出表1:
表l
x xl x2 x3 x4 x5 x6 x7
y l 3 7 13 21 31 43
记ml=y2-y1,m2=y3-y2,m3=y4-y3,m4=y5-y4,…;s1=m2-m1,S2=m3-m2,S3=m4-m3,…
(1)判断S1、S2、S3之间关系,并说明理由;
(2)若将函数“y=x2-x+1”改为“y=ax2+bx+c(a≠0)”,列出表2:
表2
x x1 x2 x3 x4 x5 x6 x7
y y1 y2 y3 y4 y5 y6 y7
其他条件不变,判断s1、s2、S3之间关系,并说明理由;
(3)小明为了通过描点法作出函数y=ax2+bx+c(a≠0)的图象,列出表3:
表3
x xl x2 x3 x4 x5 x6 x7
y 10 50 110 190 290 412 550
由于小明的粗心,表3中有一个y值算错了,请指出算错的y值(直接写答案).
8.如图-l,P为Rt△ABc所在平面内任意一点(不在直线AC上),∠ACB=90°,M为A B边中点.
操作:以PA、PC为邻边作平行四边形PADC,连结PM并延长到点E,使ME=PM,连结DE.
探究:(1)请猜想与线段DE有关的三个结论;
(2)请你利用图—2、图—3选择不同位置的点P按上述方法操作;
(3)经历(2)之后,如果你认为你写的结论是正确的,请加以证明;如果你认为你写的结论是错误的,请用图—2或图—3加以说明;(注意:错误的结论,只要你用反例给予说明也得分)
(4)若将"Rt△ABC"改为“任意△ABC",其他条件不变,利用图-4操作,并写出与线段DE有关的结论(直接写答案).
9.如图,点P(-m,m2)是抛物线E:y=x2上一点,将抛物线E沿x轴正方向平移2m个单位得到抛物线F,抛物线F的顶点为B,抛物线F交抛物线E于点A,点C是x轴上点B左侧一动点,点D是射线AB上一点,且∠ACD=∠POM.问△ACD能否为等腰三角形 若能,求点C的坐标;若不能,请说明理由.
说明:(1)如果你反复探索,没有解决问题,请写出探索过程(要求至少写3步);(2)在你完成(1)之后,可以从①②中选取一个条件,完成解答(选取①得7分;选取②得10分).①m=l;②m=2.
附加题:如图16,若将26题“点C是x轴上点B左侧一动点”改为“点C是直线y=-m2上点N左侧一动点”,其他条件不变,探究26题中的问题.
(小时)
(千米)
图①
图②
1.点P是△ABC中AB边上的一点,过点P作直线(不与直线AB重合)截△ABC,使截得的三角形与△ABC相似.满足这样条件的直线最多有____条.
2.如图,在梯形ABCD中,AD∥BC,AD=a,BC=b.若E1、F1分别是AB、DC的中点,则;若分别是的中点,则;当分别是的中点,则;若分别是的中点,根据上述规律猜想EnFn=____(n≥1,n为整数).
3.小张骑车往返于甲、乙两地,距甲地的路程y(千米)与时间x(小时)的函数图象如图所示.
(1)小张在路上停留 小时,他从乙地返回时骑车的速度为 千米/时.
(2)小李与小张同时从甲地出发,按相同路线匀速前往乙地,到乙地停止,途中小李与小张共相遇3次.请在图中画出小李距甲地的路程(千米)与时间(小时)的函数的大致图象.
(3)小王与小张同时出发,按相同路线前往乙地,距甲地的路程(千米)与时间(小时)的函数关系式为y=12x+10.小王与小张在途中共相遇几次?请你计算第一次相遇的时间.
4.如图①,正方形ABCD的顶点A,B的坐标分别为,顶点C,D在第一象限.点P从点A出发,沿正方形按逆时针方向匀速运动,同时,点Q从点E(4,0)出发,沿x轴正方向以相同速度运动.当点P到达点C时,P,Q两点同时停止运动,设运动的时间为t秒.
(1)求正方形ABCD的边长.
(2)当点P在AB边上运动时,△OPQ的面积S(平方单位)与时间t(秒)之间的函数图象为抛物线的一部分(如图②所示),求P,Q两点的运动速度.
(3)求(2)中面积S(平方单位)与时间t(秒)的函数关系式及面积取最大值时点的坐标.
(4)若点P,Q保持(2)中的速度不变,则点P沿着AB边运动时,∠OPQ的大小随着时间的增大而增大;沿着BC边运动时,∠OPQ的大小随着时间的增大而减小.当点沿着这两边运动时,使∠OPQ=90°的点有 个.
5.是他们离家的路程y(米)与时间x(分)的函数图象.妈妈骑车走了10分时接到小欣的电话,即以原速骑车前往小欣学校,并与小欣同时到达学校.已知小欣步行速度为每分钟50米,求小欣家与学校距离及小欣早晨上学需要的时间.
22.甲、乙两工程队分别承担一条2千米公路的维修工作.甲队有一半时间每天维修公路x千米,另一半时间每天维修公路y千米.乙队维修前1千米公路时,每天维修x千米;维修后1千米公路时,每天维修y千米(x≠y).
(1)求甲、乙两队完成任务需要的时间(用含x、y代数式表示);
(2)问甲、乙两队哪队先完成任务
6.如图—1、图—2分别是两个相同正方形、正六边形,其中一个正多边形的顶点在另一个正多边形外接圆圆心0处.
(1)求图—1中,重叠部分面积与阴影部分面积之比;
(2)求图—2中,重叠部分面积与阴影部分面积之比(直接写出答案);
(3)根据前面探索和图13—3,你能否将本题推广到一般的正n边形情况(n为大于2的偶数) 若能,写出推广问题和结论;若不能,请说明理由.
7.小明为了通过描点法作出函数y=x2-x+1的图象,先取自变量x的7个值满足:x2-x1=x3-x2=…=x7-x6=d,再分别算出对应的y值,列出表1:
表l
x xl x2 x3 x4 x5 x6 x7
y l 3 7 13 21 31 43
记ml=y2-y1,m2=y3-y2,m3=y4-y3,m4=y5-y4,…;s1=m2-m1,S2=m3-m2,S3=m4-m3,…
(1)判断S1、S2、S3之间关系,并说明理由;
(2)若将函数“y=x2-x+1”改为“y=ax2+bx+c(a≠0)”,列出表2:
表2
x x1 x2 x3 x4 x5 x6 x7
y y1 y2 y3 y4 y5 y6 y7
其他条件不变,判断s1、s2、S3之间关系,并说明理由;
(3)小明为了通过描点法作出函数y=ax2+bx+c(a≠0)的图象,列出表3:
表3
x xl x2 x3 x4 x5 x6 x7
y 10 50 110 190 290 412 550
由于小明的粗心,表3中有一个y值算错了,请指出算错的y值(直接写答案).
8.如图-l,P为Rt△ABc所在平面内任意一点(不在直线AC上),∠ACB=90°,M为A B边中点.
操作:以PA、PC为邻边作平行四边形PADC,连结PM并延长到点E,使ME=PM,连结DE.
探究:(1)请猜想与线段DE有关的三个结论;
(2)请你利用图—2、图—3选择不同位置的点P按上述方法操作;
(3)经历(2)之后,如果你认为你写的结论是正确的,请加以证明;如果你认为你写的结论是错误的,请用图—2或图—3加以说明;(注意:错误的结论,只要你用反例给予说明也得分)
(4)若将"Rt△ABC"改为“任意△ABC",其他条件不变,利用图-4操作,并写出与线段DE有关的结论(直接写答案).
9.如图,点P(-m,m2)是抛物线E:y=x2上一点,将抛物线E沿x轴正方向平移2m个单位得到抛物线F,抛物线F的顶点为B,抛物线F交抛物线E于点A,点C是x轴上点B左侧一动点,点D是射线AB上一点,且∠ACD=∠POM.问△ACD能否为等腰三角形 若能,求点C的坐标;若不能,请说明理由.
说明:(1)如果你反复探索,没有解决问题,请写出探索过程(要求至少写3步);(2)在你完成(1)之后,可以从①②中选取一个条件,完成解答(选取①得7分;选取②得10分).①m=l;②m=2.
附加题:如图16,若将26题“点C是x轴上点B左侧一动点”改为“点C是直线y=-m2上点N左侧一动点”,其他条件不变,探究26题中的问题.
(小时)
(千米)
图①
图②
同课章节目录
