2007年数学优等生中考复习练习(6)无答案(浙江省宁波市)
文档属性
| 名称 | 2007年数学优等生中考复习练习(6)无答案(浙江省宁波市) |
|
|
| 格式 | rar | ||
| 文件大小 | 92.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-06-11 00:00:00 | ||
图片预览


文档简介
2007年第一学期夜课甲班练习(6) 姓名:____________
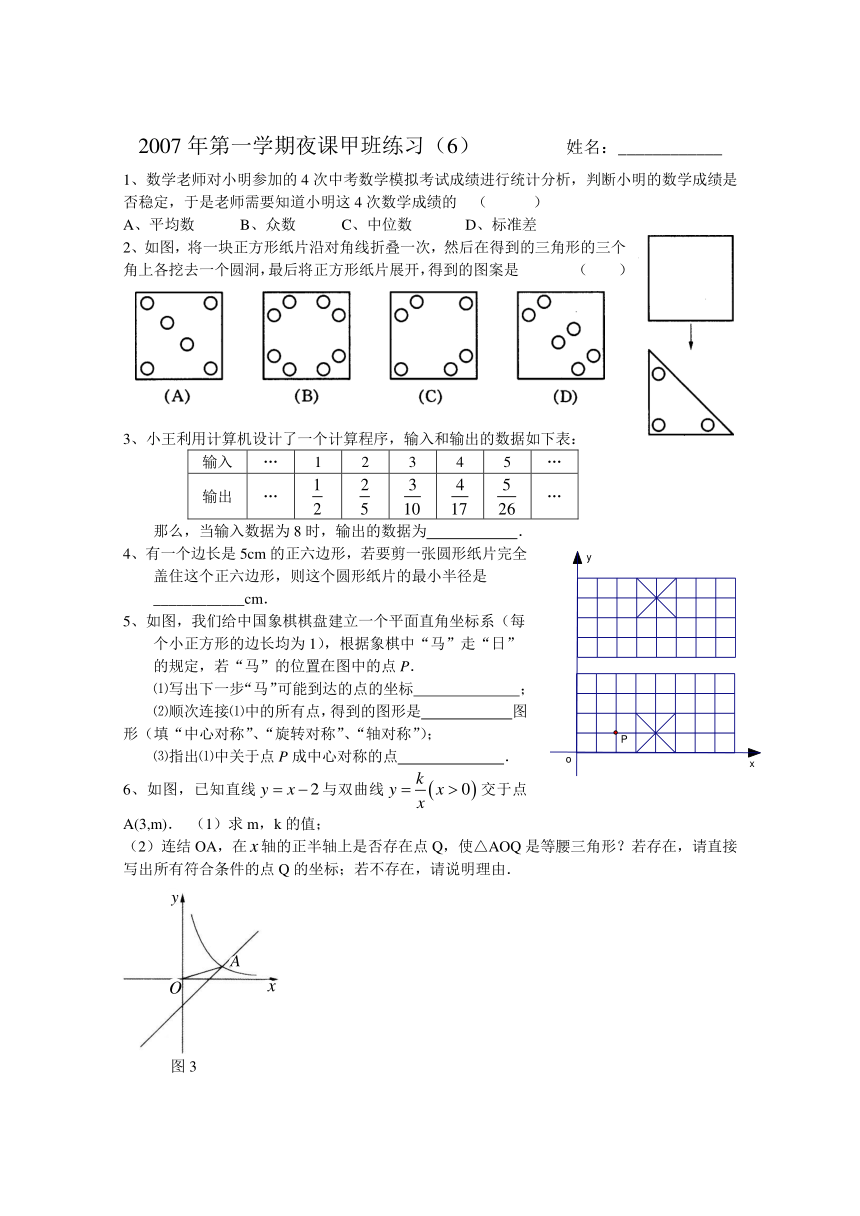
1、数学老师对小明参加的4次中考数学模拟考试成绩进行统计分析,判断小明的数学成绩是否稳定,于是老师需要知道小明这4次数学成绩的 ( )
A、平均数 B、众数 C、中位数 D、标准差
2、如图,将一块正方形纸片沿对角线折叠一次,然后在得到的三角形的三个
角上各挖去一个圆洞,最后将正方形纸片展开,得到的图案是 ( )
3、小王利用计算机设计了一个计算程序,输入和输出的数据如下表:
输入 … 1 2 3 4 5 …
输出 … …
那么,当输入数据为8时,输出的数据为 .
4、有一个边长是5cm的正六边形,若要剪一张圆形纸片完全盖住这个正六边形,则这个圆形纸片的最小半径是____________cm.
5、如图,我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长均为1),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点P.
⑴写出下一步“马”可能到达的点的坐标 ;
⑵顺次连接⑴中的所有点,得到的图形是 图形(填“中心对称”、“旋转对称”、“轴对称”);
⑶指出⑴中关于点P成中心对称的点 .
6、如图,已知直线与双曲线交于点A(3,m). (1)求m,k的值;
(2)连结OA,在轴的正半轴上是否存在点Q,使△AOQ是等腰三角形?若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.
7、如图5,某市郊外景区内一条笔直的公路a经过三个景点A,B,C.景区管委会又开发了风景优美的景点.经测量景点D位于景点A的北偏东方向8千米处,位于景点B的正北方向,还位于景点C的北偏西75°方向上.已知AB=5千米.
(1)景区管委会准备由景点D向公路a建一条距离最短的公路,不考虑其他因素,求出这条公路的长;(结果精确到0.1千米)
(2)求景点C与景点D之间的距离.(结果精确到1千米)
(参考数据:,,
,,,
,.)
8、某小型企业获得授权生产甲、乙两种奥运吉祥物,生产每种吉祥物所需材料及所获利润如下表:
A种材料() B种材料() 所获利润(元)
每个甲种吉祥物 0.3 0.5 10
每个乙种吉祥物 0.6 0.2 20
该企业现有种材料900m2,种材料850m2,用这两种材料生产甲、乙两种吉祥物共2000个.设生产甲种吉祥物x个,生产这两种吉祥物所获总利润为y元.
(1)求出y(元)与x(个)之间的函数关系式,并求出自变量的取值范围;
(2)该企业如何安排甲、乙两种吉祥物的生产数量,才能获得最大利润?最大利润是多少?
9、如图,在平面直角坐标系中,直线分别与x轴,y轴交于点A、点B.
(1)以AB为一边在第一象限内作等边△ABC及△ABC的外接圆⊙M(用尺规作图,不要求写作法,但要保留作图痕迹);
(2)若⊙M与轴的另一个交点为点,求A,B,C,D四点的坐标;
(3)求经过A,B,D三点的抛物线的解析式,并判断在抛物线上是否存在点P,使△ADP的面积等于△ADC的面积?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
10、已知抛物线y=x —4x+1.将此抛物线沿x轴方向向左平移4个单位长度,得到一条新的抛物线.
⑴求平移后的抛物线解析式;
⑵若直线y=m与这两条抛物线有且只有四个交点,求实数m的取值范围;
⑶若将已知的抛物线解析式改为y=ax +bx+c(a>0,b<0),并将此抛物线沿x轴方向向左平移 -个单位长度,试探索问题⑵.
11、操作:如图①,△ABC是正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N两点,连接MN.探究:线段BM、MN、NC之间的关系,并加以证明.
说明:⑴如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);⑵在你经历说明⑴的过程之后,可以从下列①、②中选取一个补充或更换已知条件,完成你的证明.
注意:选取①完成证明得10分;选取②完成证明得5分.
①(如图②); ②(如图③).
附加题:若点M、N分别是射线AB、CA上的点,其它条件不变,再探线段BM、MN、NC之间的关系,在图④中画出图形,并说明理由.
12、如图,△ABC是等腰直角三角形,其中CA=CB,四边形CDEF是正方形,连接AF、BD.
(1)观察图形,猜想AF与BD之间有怎样的关系,并证明你的猜想;
(2)若将正方形CDEF绕点C按顺时针方向旋转,使正方形CDEF的一边落在△ABC的内部,请你画出一个变换后的图形,并对照已知图形标记字母,题(1)中猜想的结论是否仍然成立?若成立,直接写出结论,不必证明;若不成立,请说明理由.
13、如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方).
(1)求A、B两点的坐标;
(2)设△OMN的面积为S,直线l运动时间为t秒(0≤t≤6),试求S与t的函数表达式;
(3)在题(2)的条件下,t为何值时,S的面积最大?最大面积是多少?
图3
1、数学老师对小明参加的4次中考数学模拟考试成绩进行统计分析,判断小明的数学成绩是否稳定,于是老师需要知道小明这4次数学成绩的 ( )
A、平均数 B、众数 C、中位数 D、标准差
2、如图,将一块正方形纸片沿对角线折叠一次,然后在得到的三角形的三个
角上各挖去一个圆洞,最后将正方形纸片展开,得到的图案是 ( )
3、小王利用计算机设计了一个计算程序,输入和输出的数据如下表:
输入 … 1 2 3 4 5 …
输出 … …
那么,当输入数据为8时,输出的数据为 .
4、有一个边长是5cm的正六边形,若要剪一张圆形纸片完全盖住这个正六边形,则这个圆形纸片的最小半径是____________cm.
5、如图,我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长均为1),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点P.
⑴写出下一步“马”可能到达的点的坐标 ;
⑵顺次连接⑴中的所有点,得到的图形是 图形(填“中心对称”、“旋转对称”、“轴对称”);
⑶指出⑴中关于点P成中心对称的点 .
6、如图,已知直线与双曲线交于点A(3,m). (1)求m,k的值;
(2)连结OA,在轴的正半轴上是否存在点Q,使△AOQ是等腰三角形?若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.
7、如图5,某市郊外景区内一条笔直的公路a经过三个景点A,B,C.景区管委会又开发了风景优美的景点.经测量景点D位于景点A的北偏东方向8千米处,位于景点B的正北方向,还位于景点C的北偏西75°方向上.已知AB=5千米.
(1)景区管委会准备由景点D向公路a建一条距离最短的公路,不考虑其他因素,求出这条公路的长;(结果精确到0.1千米)
(2)求景点C与景点D之间的距离.(结果精确到1千米)
(参考数据:,,
,,,
,.)
8、某小型企业获得授权生产甲、乙两种奥运吉祥物,生产每种吉祥物所需材料及所获利润如下表:
A种材料() B种材料() 所获利润(元)
每个甲种吉祥物 0.3 0.5 10
每个乙种吉祥物 0.6 0.2 20
该企业现有种材料900m2,种材料850m2,用这两种材料生产甲、乙两种吉祥物共2000个.设生产甲种吉祥物x个,生产这两种吉祥物所获总利润为y元.
(1)求出y(元)与x(个)之间的函数关系式,并求出自变量的取值范围;
(2)该企业如何安排甲、乙两种吉祥物的生产数量,才能获得最大利润?最大利润是多少?
9、如图,在平面直角坐标系中,直线分别与x轴,y轴交于点A、点B.
(1)以AB为一边在第一象限内作等边△ABC及△ABC的外接圆⊙M(用尺规作图,不要求写作法,但要保留作图痕迹);
(2)若⊙M与轴的另一个交点为点,求A,B,C,D四点的坐标;
(3)求经过A,B,D三点的抛物线的解析式,并判断在抛物线上是否存在点P,使△ADP的面积等于△ADC的面积?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
10、已知抛物线y=x —4x+1.将此抛物线沿x轴方向向左平移4个单位长度,得到一条新的抛物线.
⑴求平移后的抛物线解析式;
⑵若直线y=m与这两条抛物线有且只有四个交点,求实数m的取值范围;
⑶若将已知的抛物线解析式改为y=ax +bx+c(a>0,b<0),并将此抛物线沿x轴方向向左平移 -个单位长度,试探索问题⑵.
11、操作:如图①,△ABC是正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N两点,连接MN.探究:线段BM、MN、NC之间的关系,并加以证明.
说明:⑴如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);⑵在你经历说明⑴的过程之后,可以从下列①、②中选取一个补充或更换已知条件,完成你的证明.
注意:选取①完成证明得10分;选取②完成证明得5分.
①(如图②); ②(如图③).
附加题:若点M、N分别是射线AB、CA上的点,其它条件不变,再探线段BM、MN、NC之间的关系,在图④中画出图形,并说明理由.
12、如图,△ABC是等腰直角三角形,其中CA=CB,四边形CDEF是正方形,连接AF、BD.
(1)观察图形,猜想AF与BD之间有怎样的关系,并证明你的猜想;
(2)若将正方形CDEF绕点C按顺时针方向旋转,使正方形CDEF的一边落在△ABC的内部,请你画出一个变换后的图形,并对照已知图形标记字母,题(1)中猜想的结论是否仍然成立?若成立,直接写出结论,不必证明;若不成立,请说明理由.
13、如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方).
(1)求A、B两点的坐标;
(2)设△OMN的面积为S,直线l运动时间为t秒(0≤t≤6),试求S与t的函数表达式;
(3)在题(2)的条件下,t为何值时,S的面积最大?最大面积是多少?
图3
同课章节目录
