4.1 函数 课后作业(无答案)2023--2024学年北师大版八年级数学上册
文档属性
| 名称 | 4.1 函数 课后作业(无答案)2023--2024学年北师大版八年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 315.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-16 00:00:00 | ||
图片预览

文档简介
4.1 函数(课后作业)-北师大版八年级上册
一.选择题
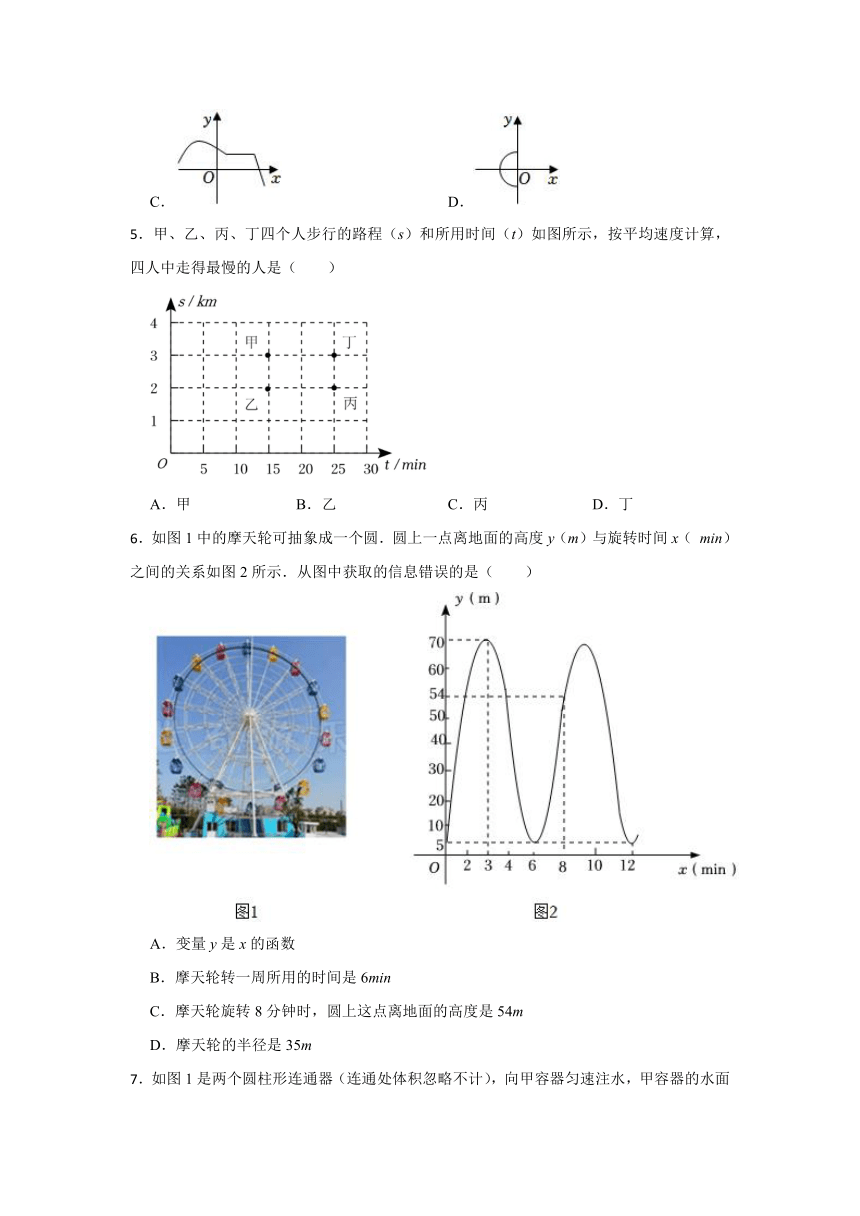
1.下列关系式中,y不是x的函数的是( )
A.y=x4 B.y=6x2+5 C.|y|=x D.y=
2.某施工队修一段长度为360米的公路,施工队每天的效率相同,如表根据每天工程进度制作而成的.
施工时间/天 1 2 3 4 5 6 7 ……
累计完成施工量/米 30 60 90 120 150 180 210 ……
下列说法错误的是( )
A.随着施工时间的逐渐增大,累计完成施工量也逐渐增大
B.施工时间每增加1天,累计完成施工量就增加30米
C.当施工时间为9天时,累计完成施工量为270米
D.若累计完成施工量为330米,则施工时间为10天
.已知点A(﹣1,1),B(1,﹣1),C(2,﹣)在同一函数图象上,这个函数图象可能是( )
A. B.
C. D.
.下列图象中,y不是x的函数的是( )
A. B.
C. D.
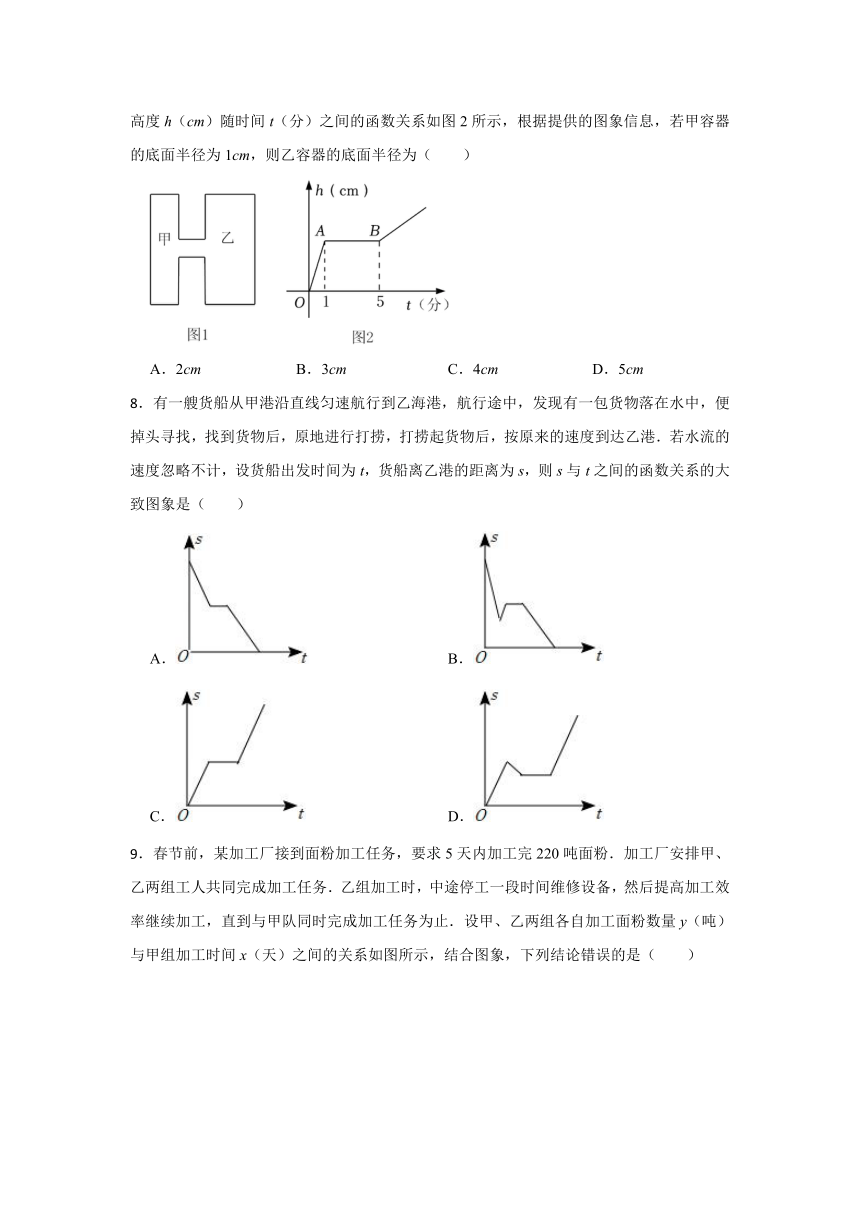
.甲、乙、丙、丁四个人步行的路程(s)和所用时间(t)如图所示,按平均速度计算,四人中走得最慢的人是( )
A.甲 B.乙 C.丙 D.丁
.如图1中的摩天轮可抽象成一个圆.圆上一点离地面的高度y(m)与旋转时间x( min)之间的关系如图2所示.从图中获取的信息错误的是( )
A.变量y是x的函数
B.摩天轮转一周所用的时间是6min
C.摩天轮旋转8分钟时,圆上这点离地面的高度是54m
D.摩天轮的半径是35m
.如图1是两个圆柱形连通器(连通处体积忽略不计),向甲容器匀速注水,甲容器的水面高度h(cm)随时间t(分)之间的函数关系如图2所示,根据提供的图象信息,若甲容器的底面半径为1cm,则乙容器的底面半径为( )
A.2cm B.3cm C.4cm D.5cm
.有一艘货船从甲港沿直线匀速航行到乙海港,航行途中,发现有一包货物落在水中,便掉头寻找,找到货物后,原地进行打捞,打捞起货物后,按原来的速度到达乙港.若水流的速度忽略不计,设货船出发时间为t,货船离乙港的距离为s,则s与t之间的函数关系的大致图象是( )
A. B.
C. D.
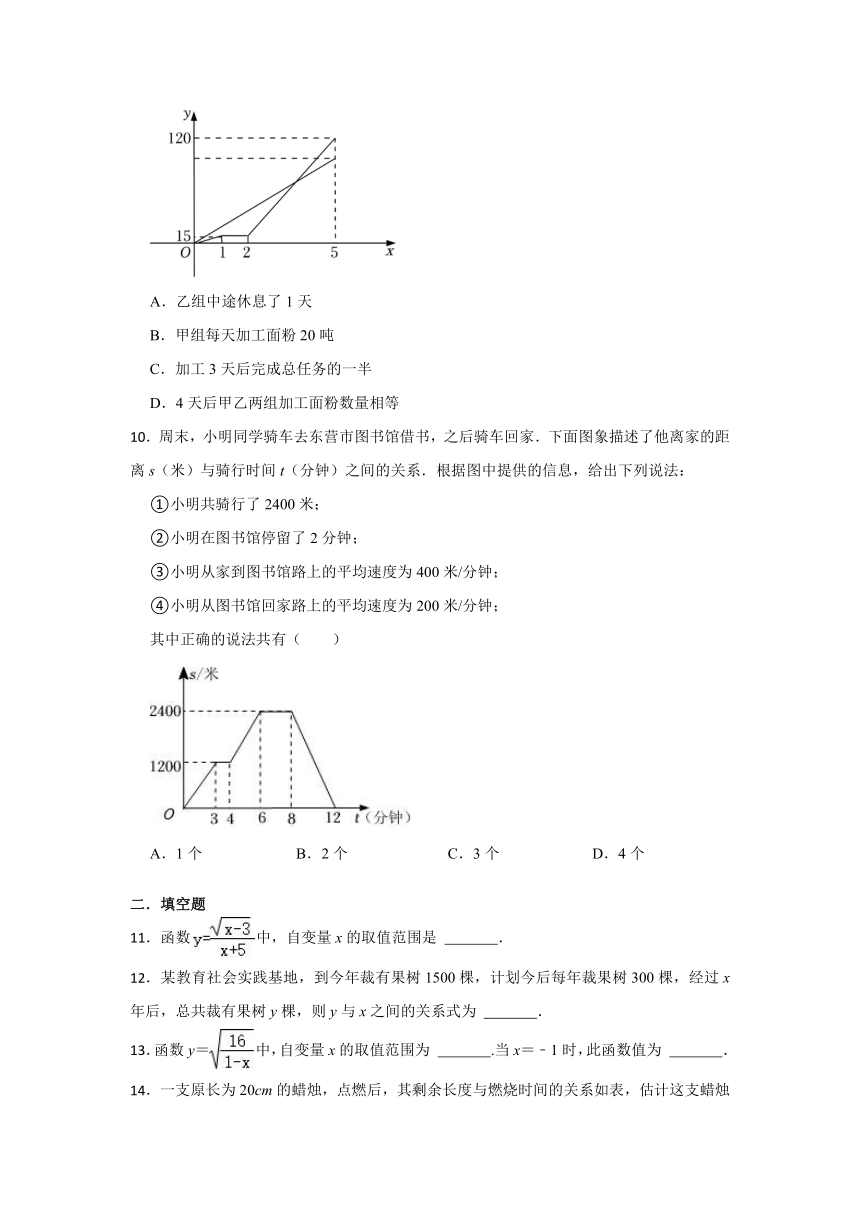
.春节前,某加工厂接到面粉加工任务,要求5天内加工完220吨面粉.加工厂安排甲、乙两组工人共同完成加工任务.乙组加工时,中途停工一段时间维修设备,然后提高加工效率继续加工,直到与甲队同时完成加工任务为止.设甲、乙两组各自加工面粉数量y(吨)与甲组加工时间x(天)之间的关系如图所示,结合图象,下列结论错误的是( )
A.乙组中途休息了1天
B.甲组每天加工面粉20吨
C.加工3天后完成总任务的一半
D.4天后甲乙两组加工面粉数量相等
.周末,小明同学骑车去东营市图书馆借书,之后骑车回家.下面图象描述了他离家的距离s(米)与骑行时间t(分钟)之间的关系.根据图中提供的信息,给出下列说法:
①小明共骑行了2400米;
②小明在图书馆停留了2分钟;
③小明从家到图书馆路上的平均速度为400米/分钟;
④小明从图书馆回家路上的平均速度为200米/分钟;
其中正确的说法共有( )
A.1个 B.2个 C.3个 D.4个
二.填空题
.函数中,自变量x的取值范围是 .
.某教育社会实践基地,到今年裁有果树1500棵,计划今后每年裁果树300棵,经过x年后,总共裁有果树y棵,则y与x之间的关系式为 .
.函数y=中,自变量x的取值范围为 .当x=﹣1时,此函数值为 .
.一支原长为20cm的蜡烛,点燃后,其剩余长度与燃烧时间的关系如表,估计这支蜡烛最多可燃烧 分钟.
燃烧时间 分 10 20 30 40 50 …
剩余长度 cm 19 18 17 16 15 …
15.某水果店每天售出某种水果的数量(单位:千克)与该水果的售价(单位:元/千克)之间的关系如表所示,由表可知,当售价为2.2元/千克时,每天能售出 千克.
售价(元/千克) 1.5 1.6 1.7 1.8 1.9 2.0 ……
数量(千克) 20 19 18 17 16 15 ……
三.解答题
16.李叔叔要用篱笆围成一个长方形的果园,已知长方形的长为50米,宽为x米.当长方形的宽由小到大变化时,长方形的面积也随之发生变化.
(1)在这个变化过程中,自变量、因变量各是什么?
(2)求长方形的面积y(平方米)与x的关系式;
(3)当长方形的宽由10米变化到25米时,长方形的面积由y1(平方米)变化到y2(平方米),求y1和y2的值.
17.周末,小明坐公交车到滨海公园,他出发后0.8小时到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往滨海公园,如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题.
(1)图中自变量是 ,因变量是 ;
(2)小明家到滨海公的路程为 km,小明在中心书城逗留的时间为 h;
(3)小明出发 小时后爸爸驾车出发;
(4)图中A点表示 ;
(5)小明从中心书城到滨海公园的平均速度为 km/h,小明爸爸驾车的平均速度为 km/h;
(6)爸爸驾车经过 h追上小明;
(7)小明从家到中心书城时,他离家路程s与坐车时间t之间的关系式为 .
18.一艘轮船在长江航线上往返于甲、乙两地.若轮船在静水中的速度不变,轮船先从甲地顺水航行到乙地,停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用的时间为t(小时),航行的路程为s(千米),s与t的函数图象如图所示.
(1)图中自变量是 ,因变量是 ;(用字母表示)
(2)甲乙两地相距 千米,轮船在乙地停留了 小时;
(3)求出轮船顺水航行时航行的路程s关于所用时间t的函数关系式,并写出自变量的取值范围;
(4)如果轮船从乙地逆水航行返回到甲地时的速度为20千米/小时,直接写出点M的坐标是 .
19.小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系式示意图.根据图中提供的信息回答下列问题:
(1)小红家到舅舅家的路程是 米,小红在商店停留了 分钟;
(2)在整个去舅舅家的途中时间段小红骑车速度最快,最快的速度 米/分.
(3)本次去舅舅家的行程中,小红一共行驶了多少米?一共用了多少分钟?
20.已知函数y=,某兴趣小组对其图象与性质进行了探究,请补充完整探究过程.
下表是该函数y与自变量x的几组对应值,请解答下列问题:
x … ﹣5 ﹣4 ﹣3 ﹣2 ﹣ ﹣1 ﹣ 0 1 2 3 4 5 8 …
y … 1 m 0 ﹣ ﹣2 ﹣ ﹣5 ﹣6 n ﹣2 …
(1)根据图表数据,可得出函数y=中待定系数a= ,b= ,自变量x的取值范围是 ;
(2)表中m的值为 ;n的值为 ;
(3)请你根据上表中的数据在平面直角坐标系中描点、连线,补全该函数图象,并写出该函数的一条性质 ;
(4)若,结合图象,直接写出x的取值范围.
一.选择题
1.下列关系式中,y不是x的函数的是( )
A.y=x4 B.y=6x2+5 C.|y|=x D.y=
2.某施工队修一段长度为360米的公路,施工队每天的效率相同,如表根据每天工程进度制作而成的.
施工时间/天 1 2 3 4 5 6 7 ……
累计完成施工量/米 30 60 90 120 150 180 210 ……
下列说法错误的是( )
A.随着施工时间的逐渐增大,累计完成施工量也逐渐增大
B.施工时间每增加1天,累计完成施工量就增加30米
C.当施工时间为9天时,累计完成施工量为270米
D.若累计完成施工量为330米,则施工时间为10天
.已知点A(﹣1,1),B(1,﹣1),C(2,﹣)在同一函数图象上,这个函数图象可能是( )
A. B.
C. D.
.下列图象中,y不是x的函数的是( )
A. B.
C. D.
.甲、乙、丙、丁四个人步行的路程(s)和所用时间(t)如图所示,按平均速度计算,四人中走得最慢的人是( )
A.甲 B.乙 C.丙 D.丁
.如图1中的摩天轮可抽象成一个圆.圆上一点离地面的高度y(m)与旋转时间x( min)之间的关系如图2所示.从图中获取的信息错误的是( )
A.变量y是x的函数
B.摩天轮转一周所用的时间是6min
C.摩天轮旋转8分钟时,圆上这点离地面的高度是54m
D.摩天轮的半径是35m
.如图1是两个圆柱形连通器(连通处体积忽略不计),向甲容器匀速注水,甲容器的水面高度h(cm)随时间t(分)之间的函数关系如图2所示,根据提供的图象信息,若甲容器的底面半径为1cm,则乙容器的底面半径为( )
A.2cm B.3cm C.4cm D.5cm
.有一艘货船从甲港沿直线匀速航行到乙海港,航行途中,发现有一包货物落在水中,便掉头寻找,找到货物后,原地进行打捞,打捞起货物后,按原来的速度到达乙港.若水流的速度忽略不计,设货船出发时间为t,货船离乙港的距离为s,则s与t之间的函数关系的大致图象是( )
A. B.
C. D.
.春节前,某加工厂接到面粉加工任务,要求5天内加工完220吨面粉.加工厂安排甲、乙两组工人共同完成加工任务.乙组加工时,中途停工一段时间维修设备,然后提高加工效率继续加工,直到与甲队同时完成加工任务为止.设甲、乙两组各自加工面粉数量y(吨)与甲组加工时间x(天)之间的关系如图所示,结合图象,下列结论错误的是( )
A.乙组中途休息了1天
B.甲组每天加工面粉20吨
C.加工3天后完成总任务的一半
D.4天后甲乙两组加工面粉数量相等
.周末,小明同学骑车去东营市图书馆借书,之后骑车回家.下面图象描述了他离家的距离s(米)与骑行时间t(分钟)之间的关系.根据图中提供的信息,给出下列说法:
①小明共骑行了2400米;
②小明在图书馆停留了2分钟;
③小明从家到图书馆路上的平均速度为400米/分钟;
④小明从图书馆回家路上的平均速度为200米/分钟;
其中正确的说法共有( )
A.1个 B.2个 C.3个 D.4个
二.填空题
.函数中,自变量x的取值范围是 .
.某教育社会实践基地,到今年裁有果树1500棵,计划今后每年裁果树300棵,经过x年后,总共裁有果树y棵,则y与x之间的关系式为 .
.函数y=中,自变量x的取值范围为 .当x=﹣1时,此函数值为 .
.一支原长为20cm的蜡烛,点燃后,其剩余长度与燃烧时间的关系如表,估计这支蜡烛最多可燃烧 分钟.
燃烧时间 分 10 20 30 40 50 …
剩余长度 cm 19 18 17 16 15 …
15.某水果店每天售出某种水果的数量(单位:千克)与该水果的售价(单位:元/千克)之间的关系如表所示,由表可知,当售价为2.2元/千克时,每天能售出 千克.
售价(元/千克) 1.5 1.6 1.7 1.8 1.9 2.0 ……
数量(千克) 20 19 18 17 16 15 ……
三.解答题
16.李叔叔要用篱笆围成一个长方形的果园,已知长方形的长为50米,宽为x米.当长方形的宽由小到大变化时,长方形的面积也随之发生变化.
(1)在这个变化过程中,自变量、因变量各是什么?
(2)求长方形的面积y(平方米)与x的关系式;
(3)当长方形的宽由10米变化到25米时,长方形的面积由y1(平方米)变化到y2(平方米),求y1和y2的值.
17.周末,小明坐公交车到滨海公园,他出发后0.8小时到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往滨海公园,如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题.
(1)图中自变量是 ,因变量是 ;
(2)小明家到滨海公的路程为 km,小明在中心书城逗留的时间为 h;
(3)小明出发 小时后爸爸驾车出发;
(4)图中A点表示 ;
(5)小明从中心书城到滨海公园的平均速度为 km/h,小明爸爸驾车的平均速度为 km/h;
(6)爸爸驾车经过 h追上小明;
(7)小明从家到中心书城时,他离家路程s与坐车时间t之间的关系式为 .
18.一艘轮船在长江航线上往返于甲、乙两地.若轮船在静水中的速度不变,轮船先从甲地顺水航行到乙地,停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用的时间为t(小时),航行的路程为s(千米),s与t的函数图象如图所示.
(1)图中自变量是 ,因变量是 ;(用字母表示)
(2)甲乙两地相距 千米,轮船在乙地停留了 小时;
(3)求出轮船顺水航行时航行的路程s关于所用时间t的函数关系式,并写出自变量的取值范围;
(4)如果轮船从乙地逆水航行返回到甲地时的速度为20千米/小时,直接写出点M的坐标是 .
19.小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系式示意图.根据图中提供的信息回答下列问题:
(1)小红家到舅舅家的路程是 米,小红在商店停留了 分钟;
(2)在整个去舅舅家的途中时间段小红骑车速度最快,最快的速度 米/分.
(3)本次去舅舅家的行程中,小红一共行驶了多少米?一共用了多少分钟?
20.已知函数y=,某兴趣小组对其图象与性质进行了探究,请补充完整探究过程.
下表是该函数y与自变量x的几组对应值,请解答下列问题:
x … ﹣5 ﹣4 ﹣3 ﹣2 ﹣ ﹣1 ﹣ 0 1 2 3 4 5 8 …
y … 1 m 0 ﹣ ﹣2 ﹣ ﹣5 ﹣6 n ﹣2 …
(1)根据图表数据,可得出函数y=中待定系数a= ,b= ,自变量x的取值范围是 ;
(2)表中m的值为 ;n的值为 ;
(3)请你根据上表中的数据在平面直角坐标系中描点、连线,补全该函数图象,并写出该函数的一条性质 ;
(4)若,结合图象,直接写出x的取值范围.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
